|
Ковтюх Марина Кимовна, учитель математики МАОУ «Лянторская СОШ №7»
ФИО педагога
|
Ковтюх Марина Кимовна, учитель математики МАОУ«Лянторская СОШ №7»
|
Программа
|
Л.С. Атанасян учебник «Геометрия 7-9» Москва «Просвещение» 2016 г
|
Тема урока
|
Теорема Пифагора
|
Задачи урока
|
Научить применять теорему Пифагора при решении задач, расширить круг геометрических задач, решаемых школьниками.
Развивать метапредметные УУД.
Воспитать: познавательный интерес к новым знаниям; ответственность за сказанное слово; способность к самооценке на основе наблюдения за собственной речью.
|
Планируемые результаты
|
Личностные:
проявлять познавательный интерес к новым знаниям;
воспитывать ответственность за сказанное слово;
стремиться к речевому самосовершенствованию;
прививать способность к самооценке на основе наблюдения за выполнение учебной задачи.
Метапредметные:
Регулятивные УУД
принятие учебно-познавательной задачи и сохранение её до конца учебных действий;
планирование действий в соответствии с учебно-познавательными задачами урока;
действие согласно составленному плану (алгоритму), а также по инструкциям учителя или дидактического задания;
контроль за своими действия и действиями одноклассников;
оценивание результатов деятельности.
Коммуникативные УУД
развитие умения работать с информацией на уроке, связно излагать мысли;
высказывание своего мнения и аргументирование своей точки зрения и оценки полученного результата;
соблюдение правил работы в динамических группах, умение договариваться и приходить к общему решению в совместной деятельности;
планирование ученического сотрудничества с учителем и сверстниками.
Познавательные УУД
Предметные:
знать формулировку теоремы Пифагора;
показать её применение в ходе решения задач;
расширить круг геометрических задач, решаемых школьниками.
|
Методы обучения
|
По источникам знаний: словесный, наглядный, практический.
По степени взаимодействия учителя и учащегося: беседа, рассказ, объяснение, учебное исследование, самостоятельная работа.
По характеру познавательной деятельности учащихся и участия учителя в учебной деятельности: объяснительно - иллюстративный, учебно-исследовательский, системно-деятельностный, анализ, синтез знаний.
Метод проверки, оценки знаний и УУД: фронтальный опрос, самоконтроль, анализ, синтез, рефлексия.
Педагогический приём: «Ситуация успеха»
|
Тип урока
|
Урок «открытия» новых знаний
|
Форма организации учебно-познавательной деятельности
|
Коллективная, групповая
|
Учебно - наглядные пособия, атрибуты
|
Учебная литература:
-учебник: Геометрия 7-9 классы. Учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов.
Учебно - наглядные пособия для выполнения практического задания и самостоятельной работы:
-карточки-задания для работы в группе и индивидуальной самостоятельной работы;
-презентация к уроку для учащихся по теме «Теорема Пифагора»
|
Технические средства информации
|
Интерактивный комплекс с программным обеспечением WindowsXР и программа MicrosoftOffice-PowerPoint.
|
Технологическая карта урока
Дидактическая задача этапа
|
Деятельность учителя
|
Деятельность учащихся
|
Принципы системно-деятельностного подхода, формируемые УУД.
|
1этап. Мотивации к учебной деятельности
|
Мотивировать учащихся к учебной деятельности посредством создания эмоциональной обстановки.
|
Приветственное слово учителя:
Здравствуйте дорогие друзья, я рада всех вас видеть на сегодняшнем уроке.
|
Приветствуют учителя.
Настраиваются на урок, психологически готовятся к общению.
|
Принцип психологической комфортности.
УУД: личностные, коммуникативные.
Цель – создание доброжелательной атмосферы, мотивация на учёбу, создание ситуации успеха.
|
2 этап. Актуализации, локализации индивидуальных затруднений для определения темы урока, цели выполнения учебной задачи.
|
Создать проблемную ситуацию, спрогнозировать предстоящую деятельность.
|
“Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень”. Иоганн Кеплер.
Чтобы понять о чем пойдет речь сегодня на уроке, предлагаю ответить на вопросы.
Учитель предлагает решить задачу (создание проблемной ситуации).
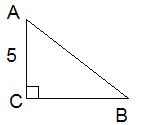
Площадь треугольника АВС равна 30 см2, АС=5 см.
Найдите периметр треугольника
Какую трудность вы встретили при решении этой задачи?
|
Учащиеся отвечают на вопросы (приложение 1)
Из условия задачи можно найти длину катета ВС, а для нахождения периметра треугольника неизвестна гипотенуза АВ.
Мы не знаем формулу для нахождения гипотенузы АВ.
|
Принцип деятельности.
УУД: регулятивные (проблемная подача учебного материала).
Принцип целостности.
УУД: познавательные, регулятивные (самостоятельное формулирование цели, планирование, прогнозирование)
Регулятивные УУД: осознавать самого себя как движущую силу своего научения, свою способность к преодолению препятствий и самокоррекции.
|
3 этап. Изучение новых знаний и способов действий.
|
Познакомить учащихся с теоремой Пифагора и показать её применение в ходе решения задач
|
Практическое задание.
Каждой группе (класс разбит на три группы) выдаются различные прямоугольные треугольники. Нужно измерить стороны треугольника и найти общую закономерность.
Посмотрите внимательно на каждую строчку.
Есть ли какая-то закономерность?
Запишите закономерность буквенным выражением
а2 + b2 = c2
Мы с вами практически проверили, что в прямоугольном треугольнике выполняется такое равенство, а сейчас это докажем. Данное утверждение носит название «Теорема Пифагора».
-Давайте, определим тему нашего урока.
-Итак, тема нашего урока « Теорема Пифагора».
- ую и за
Запишите тему урока в тетрадь.
(слайд 7-8) – краткая биография Пифагора
В научной литературе зафиксировано 370 доказательств этой теоремы. Дома вы рассмотрите доказательство из учебника, а сейчас рассмотрим доказательство, которое подготовила ученица нашего класса _Свалова Татьяна. Разбирается доказательство (слайд 9-18 )
А теперь возвращаемся к задаче, которую не смогли решить.
П лощадь треугольника АВС равна 30 см2, АС=5 см. лощадь треугольника АВС равна 30 см2, АС=5 см.
Найдите периметр треугольника (слайд 19)
Зная два катета, теперь мы можем найти гипотенузу и периметр.
Сейчас прослушаем стихотворение, которое помогает запомнить формулировку теоремы Пифагора. (слайд 20)
Если дан нам треугольник
И притом с прямым углом
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим
Сумму степеней находим
И таким простым путем
К результату мы придем. (И. Дырченко)
|
Учащиеся измеряют стороны треугольников, результаты заносят в таблицу, находящуюся на столе у каждой группы и сверяют с доской (слайд 6)
Целеполагание:
Познакомиться с теоремой Пифагора и показать её применение в ходе решения задач;
Уметь делать логические выводы из полученного результата
Учащиеся записывают тему урока
Используя теорему Пифагора, учащиеся находят гипотенузу и периметр треугольника.
|
Принцип деятельности. УУД: коммуникативные, познавательные, регулятивные (развитие внимания учащихся, монологической речи; создание благоприятной атмосферы заинтересованности; работа над формированием логических умений: анализ, сравнение, обобщение, построение цепочек рассуждений).
УУД: регулятивные (прогнозировать, слушать собеседника, умение выражать свою точку зрения).
познавательные: формировать умения работать с информацией, выполнять логические операции самостоятельно.
Коммуникативные
Регулятивные УУД
проявлять познавательную инициативу в учебном сотрудничестве
|
4 этап. Закрепления изученного, обобщения и систематизации.
|
Расширить круг геометрических задач, решаемых при помощи теоремы Пифагора
|
Практическое применение теоремы.
Раньше при строительстве получали прямой угол с помощью веревки, разделенной на 12 равных частей. У вас на столе лежат такие веревочки. Подумайте, как можно использовать эту веревку для построения прямого угла.
Треугольник со сторонами 3, 4 и 5 называется Египетским треугольником.
Тренажер (слайд 21-23)
а) Найти неизвестную сторону треугольника.

3 х
4

б) Найти периметр ромба
АС=12м; ВD = 16м
Решение задач на применение теоремы
Работают в группах (слайд 28- 30)
Учитель предлагает учащимся поработать индивидуально, выбрать задачи из предложенных и решить.
Задача 1. (2 балла)
Боковая сторона равнобедренного треугольника равна 10см, а высота, проведенная к основанию, равна 6 см. Найти площадь треугольника.
Задача 2. (3 балла)
Сторона ромба равна 13см, а одна из диагоналей 10см. Найти вторую диагональ ромба.
Задача 3. (4 балла)
Две вышки находятся на расстоянии 60 метров одна от другой.
Высота первой вышки 50 метров, а высота второй 40 метров.
Между вышками находится колодец, одинаково удаленный от вершин башен.
Как далеко находится колодец от оснований высокой вышки?
А
 D D
50
К 40
С B
60
Правильные ответы (слайд 25)
|
Учащиеся с помощью веревочки пробуют построить прямоугольный треугольник, используя заданное количество узелков. Результат демонстрируют учителю. Делают вывод, что можно построить треугольник только со сторонами 3,4 и 5.
Учащиеся решают задачи на применение теоремы Пифагора устно (тренажер).
Учащиеся решают задачи на применение теоремы Пифагора, подобранные из различных источников (древнерусская задача, задача из китайской «Математики в девяти книгах», задача из учебника «Арифметика» Леонтия Магницкого). (Приложение2)
Каждый выбирает для себя задачу (одну или две) и решает самостоятельно.
Ответы к задаче записывают в бланках, затем ребята обмениваются бланками и делают взаимопроверку (приложение 3)
|
Личностные: формирование мотивации
Регулятивные: целеполагание, контроль (сопоставление результата действия с эталоном)
Познавательные: анализ, синтез.
Принцип деятельности. УУД: коммуникативные, познавательные, регулятивные (развитие внимания учащихся, монологической речи; создание благоприятной атмосферы заинтересованности; работа над формированием логических умений: анализ, сравнение, обобщение, построение цепочек рассуждений).
УУД: регулятивные (прогнозировать, слушать собеседника, умение выражать свою точку зрения).
познавательные: формировать умения работать с информацией, выполнять логические операции самостоятельно.
Коммуникативные
Регулятивные УУД
проявлять познавательную инициативу в учебном сотрудничестве.
|
5 этап. Рефлексия учебной деятельности на уроке
|
Самооценка обучающимися результатов своей учебной деятельности, осознание метода построения и границ применения нового способа действия; создание эмоционального результата урока
|
«Из посвящений теореме Пифагора А. Шамиссо»
(слайд 31)
Пробудет вечно истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в ее далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сот быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков
Поэтому всегда с тех пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор
Беседа с учащимися
Предлагает дополнить предложение:
1) Я познакомился …
2) Я научился …
3) Я могу …
4) Мне очень понравилось….
5) Мне не понравилось….
6) Я бы хотел изменить….
У вас на столе лежат карточки, представьте, что это вы и закончите рисунок
1   . Иду на урок 2. На уроке 3. После урока . Иду на урок 2. На уроке 3. После урока
|
Учащиеся делятся впечатлениями от проделанной работы, отмечают трудности, которые у них возникли в ходе работы
Отвечают на вопросы учителя.
|
Личностные
воспитывать ответственность за сказанное слово;
прививать способность к самооценке на основе наблюдения за выполнение учебной задачи.
Регулятивные УУД
контроль за своими действия и действиями одноклассников;
оценивание результатов деятельности;
выявление причинно-следственных связей в окружающем мире.
Коммуникативные УУД
высказывание своего мнения и аргументирование своей точки зрения и оценки полученного результата.
Познавательные УУД
-анализировать, делать выводы.
|
6 этап. Домашнее задание с элементами выбора.
|
Наметить цель дальнейшей деятельности и в соответствии с результатами деятельности на уроке согласовать задание для самоподготовки
|
Теоретический материал по учебнику (для всех);
по выбору
мини-сочинение на тему «Зачем нужна теорема Пифагора?»;
найти ещё одно доказательство теоремы Пифагора;
фронтон Большого театра в Москве имеет форму равнобедренного треугольника с боковыми сторонами по 21,5 м и основанием 42 м (размеры приближены). Вычислите площадь фронтона;
д аны отрезки a и b, а = 5 см, b = 7 см. Постройте отрезок аны отрезки a и b, а = 5 см, b = 7 см. Постройте отрезок
|
Каждый учащийся получают индивидуальное домашнее задание (приложение 4)
|
| |
 Скачать 64.15 Kb.
Скачать 64.15 Kb.