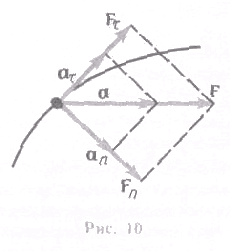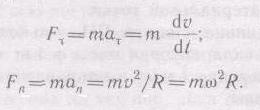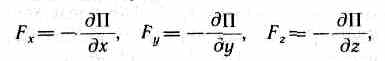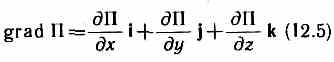Пространство и время в классической механике. Система отсчета.
В механике движением называют изменения положения тел в пространстве с течением времени. Под положением здесь понимается относительное положение, т.е., положение тела относительно других тел.
В механике для описания движения тел в зависимости от условий конкретных задач используются разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Материальная точка — понятие абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет но орбитам вокруг Солнца, можно принять их за материальные точки
Тело отсчета – положение материальной точки определяется по отношению, к какому- либо другому, произвольно выбранному телу.
Система отсчета – совокупность системы координат и часов.
Существуют два вида координатных систем – правая и левая системы. Их различают с помощью правила буравчика.
Положение каждой точки в избранной пространственной системе можно задавать тремя числами – координатами точки x,y,z. Три координаты x,y,z можно объединить в один направленный отрезок, называемый радиусом-вектором r, проведенный из начала координат в рассматриваемую точку. Координаты x,y,zявляются его проекциями на координатные оси, а потому r=xi+yj+zk,где i,j,k – координатные орты, т.е. единичные векторы, направленные вдоль координатных осей X,Y,Z.
Тело или система отсчета, относительно которых определяется положение остальных тел, называется пространственной системой отсчета.
Как и всякая физическая величина, время количественно характеризуется некоторыми числами. Задача прежде всего состоит в том, чтобы выяснить, с помощью каких принципиальных измерительных операций эти числа могут быть получены. Тем самым устанавливается и точный смысл этих чисел.
Под временем в количественном смысле этого слова мы будем понимать показания каких- то часов. Часы здесь понимаются в более широком смысле слова. Под часами понимают любое тело или систему тел, в которых совершается периодический процесс, служащий для измерения времени.
Необходимо подчеркнуть однородность и изотропию пространства и однородность времени. Однородность пространства означает, что в нем все пространственные точки эквивалентны, т.е. ничем не выделены одна от другой. Изотропия пространства характеризуется отсутствием в нем выделенных направлений – все направления в пространстве эквивалентны.
Однородность времени означает то же самое по отношению к любым моментам времени.
Поступательное движение твердого тела. Твердое тело как материальная точка. Вращение твердого тела вокруг неподвижной оси.
Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек.
Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело.
Абсолютно твердым называют тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным. Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений.
Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При этом все точки тела движутся одинаково, т.е. с одинаковыми скоростями и ускорениями. При этом все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости υ и ускорения a . Поступательное движение может быть не только прямолинейным, но и криволинейным, и в этом случае все точки тела также описывают одинаковые траектории.
Для поступательного движения абсолютно твердого тела постоянной массы справедливо такое же уравнение, как и для материальной точки.
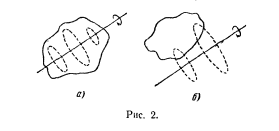
Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Ось вращения может находиться вне тела.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости; 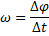
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
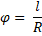
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
Число полных оборотов за единицу времени называют частотой обращения. 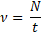
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т. 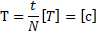 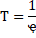 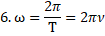 .Связь между линейной и угловой скоростями: .Связь между линейной и угловой скоростями: 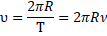 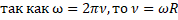 . Связь между ускорением и угловой скоростью: . Связь между ускорением и угловой скоростью: 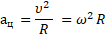
Скорость и ускорение частицы в различных системах отсчета.
Обычно на практике механическое движение какого-то тела могут изучать несколько наблюдателей, находящихся в различных системах отсчета. В связи с этим возникает необходимость в сравнении результатов, полученных в различных системах отсчета. И, кроме того, от выбора системы отсчета зависит объем вычислений при решении практических задач. Заметим, что ниже приведенные соотношения справедливы для скоростей движения значительно меньших скорости света в вакууме (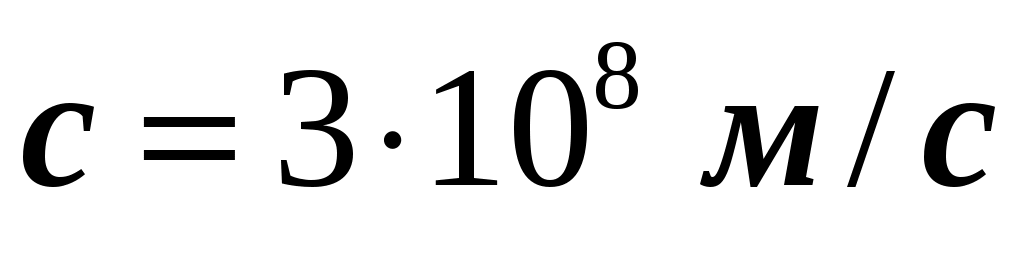 ). ).
Постановка задачи. Имеются две произвольные системы отсчета  и и 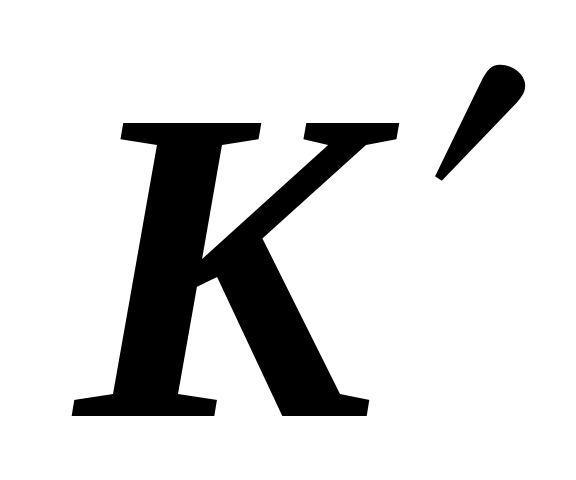 , движущиеся относительно друг друга. Известны скорость , движущиеся относительно друг друга. Известны скорость 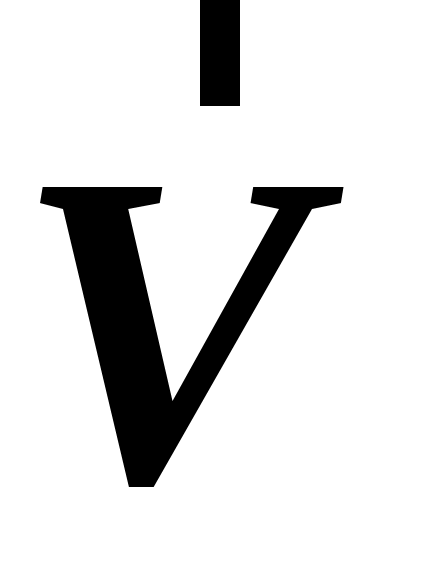 и ускорение и ускорение 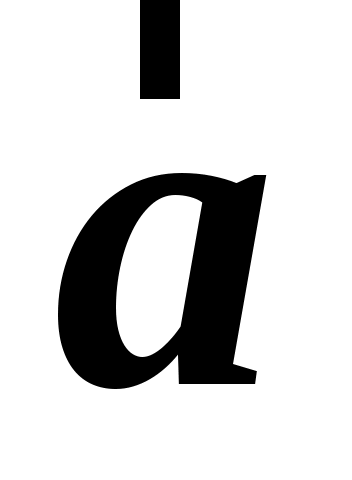 точки точки  в в 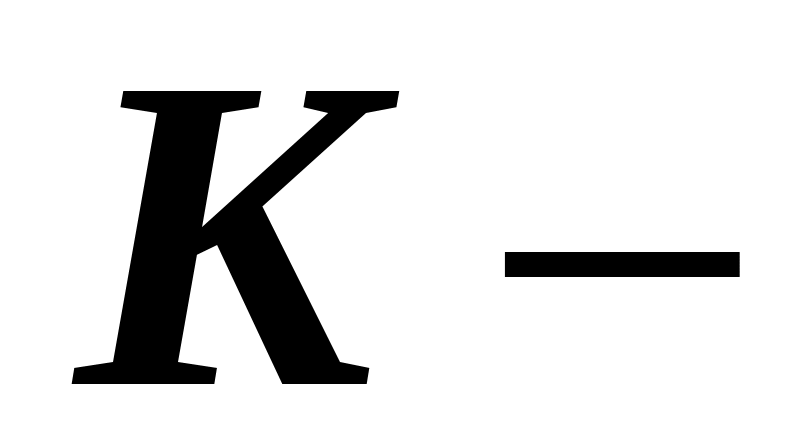 системе. Каковы значения величин системе. Каковы значения величин 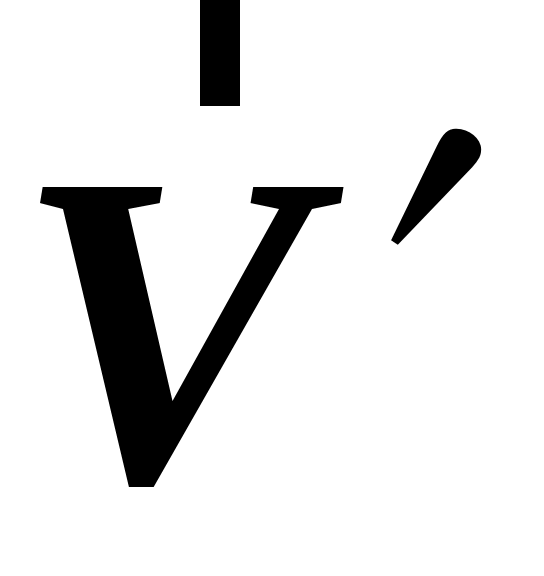 и и 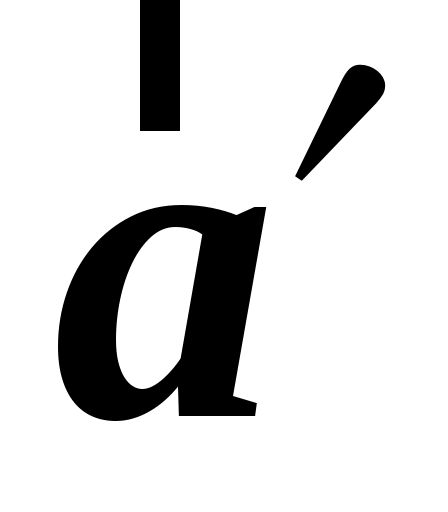 в в  системе. системе.
Рассмотрим три наиболее важных случая движения одной системы отсчета относительно другой.
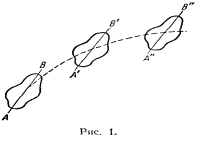
1. система движется поступательно по отношению система движется поступательно по отношению 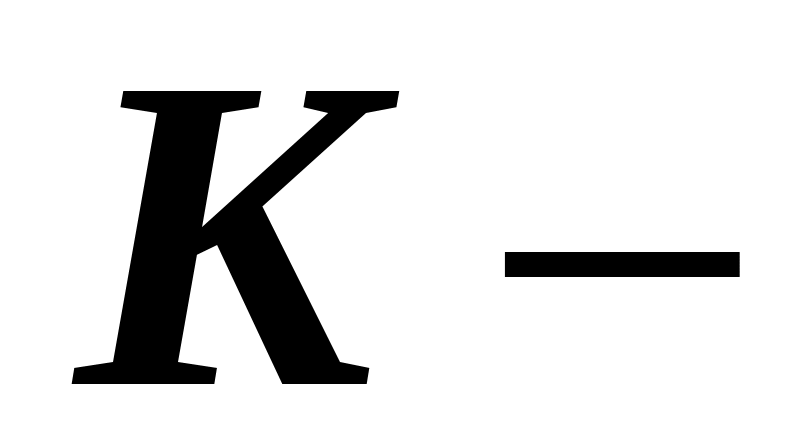 системе. Пусть положение движущейся точки системе. Пусть положение движущейся точки  в в 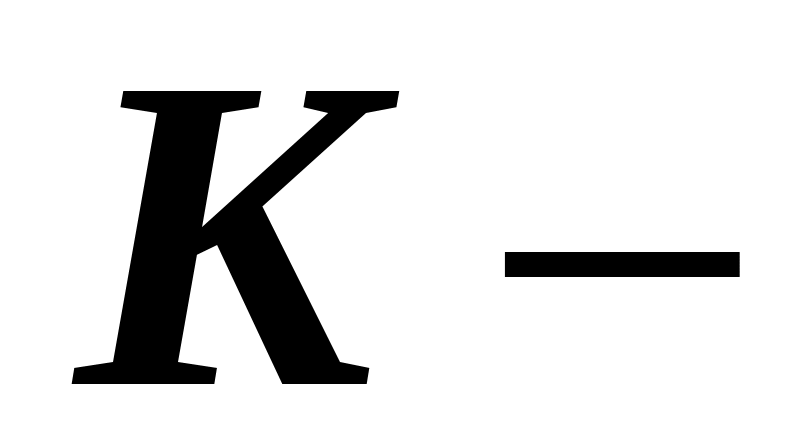 системе определяется радиус–вектором системе определяется радиус–вектором 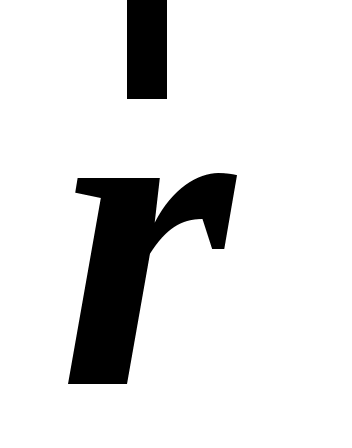 , а в , а в  системе –– радиус–вектором системе –– радиус–вектором 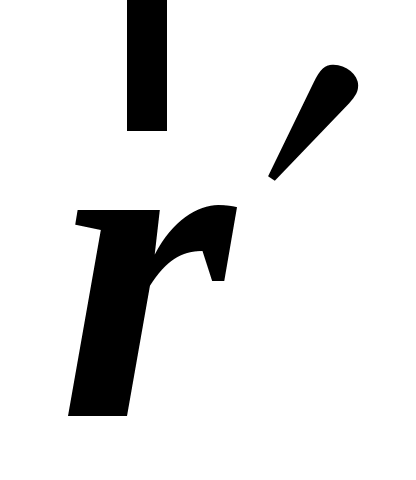 (см. рис. 1.7). (см. рис. 1.7).  система движется поступательно относительно система движется поступательно относительно 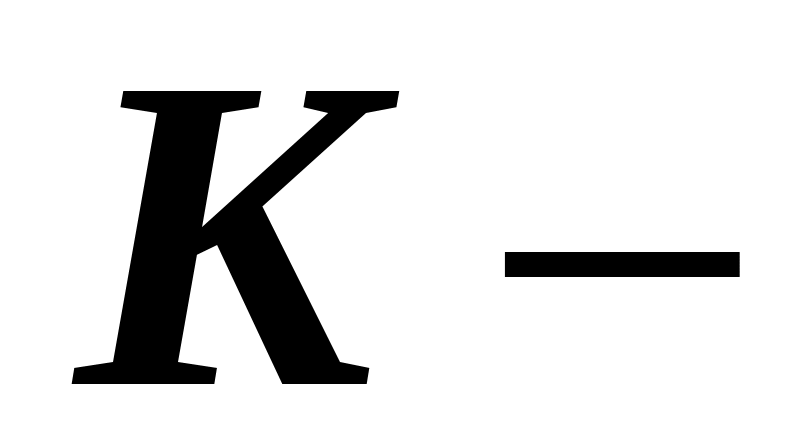 системы. Положение начала отсчета системы. Положение начала отсчета  системы (точка системы (точка 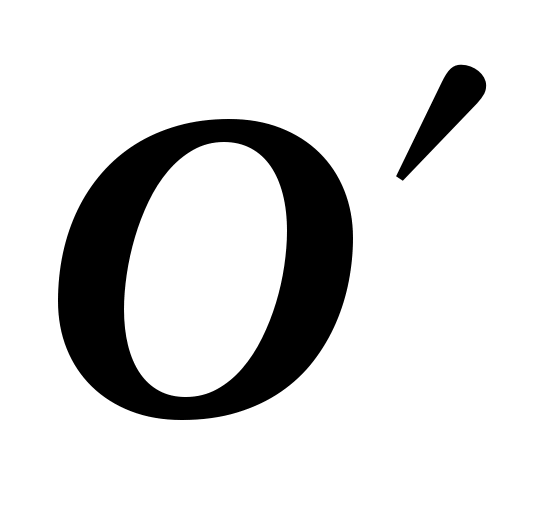 ) определяет радиус–вектор ) определяет радиус–вектор 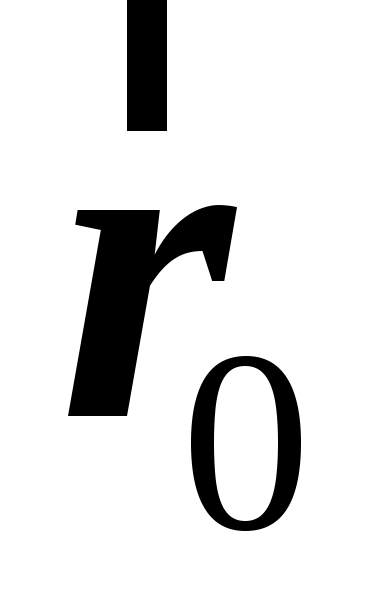 . .
О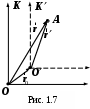 чевидно что, векторы чевидно что, векторы 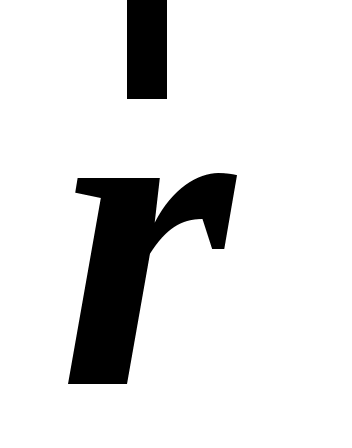 и и 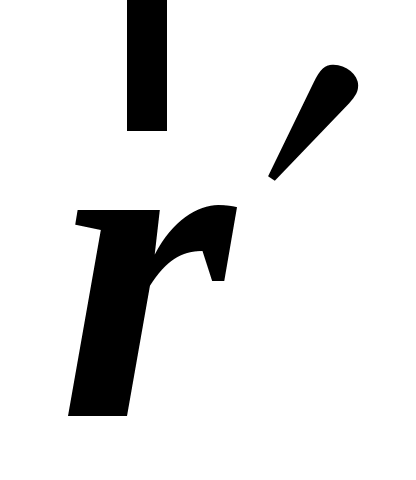 связаны соотношением: связаны соотношением:
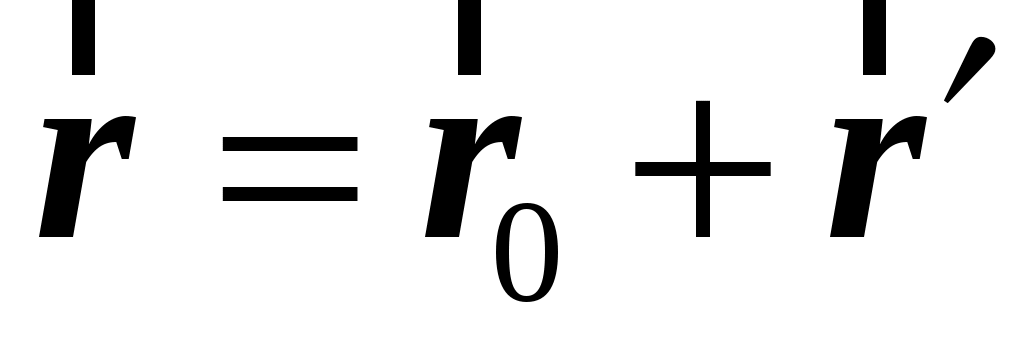 . (1.41) . (1.41)
Для бесконечно малых перемещений 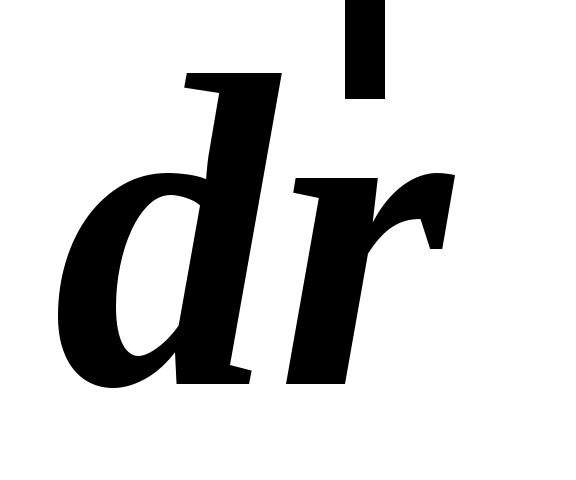 и и 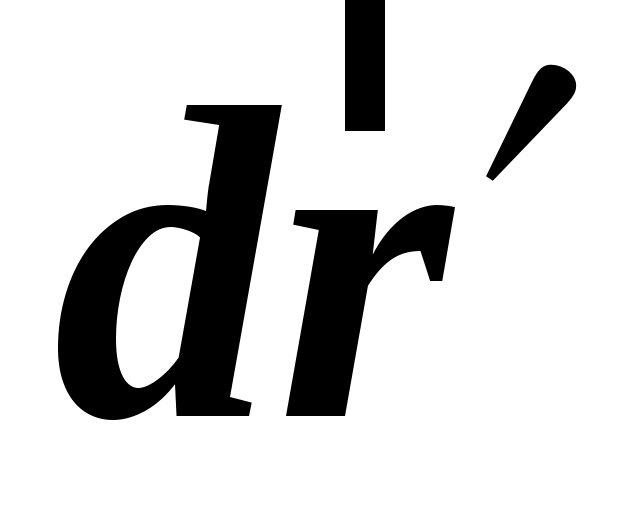 точки точки  соответственно в соответственно в  и и  системах справедлива формула: системах справедлива формула:
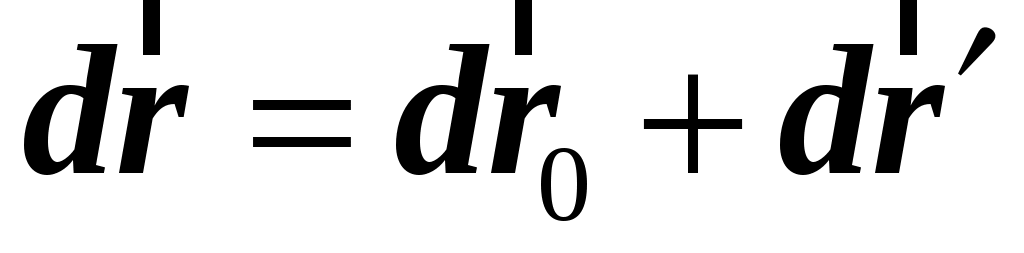 . (1.42) . (1.42)
Скорости точки  ( (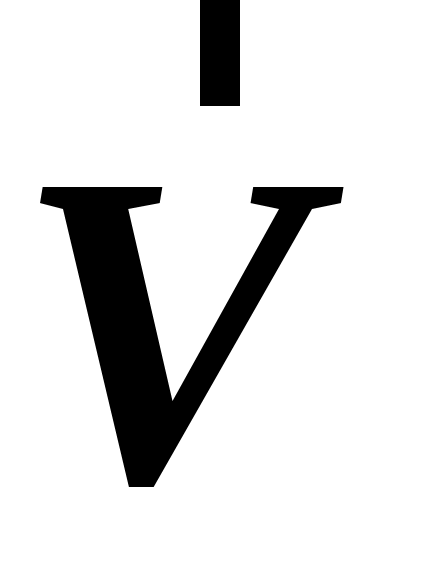 и и 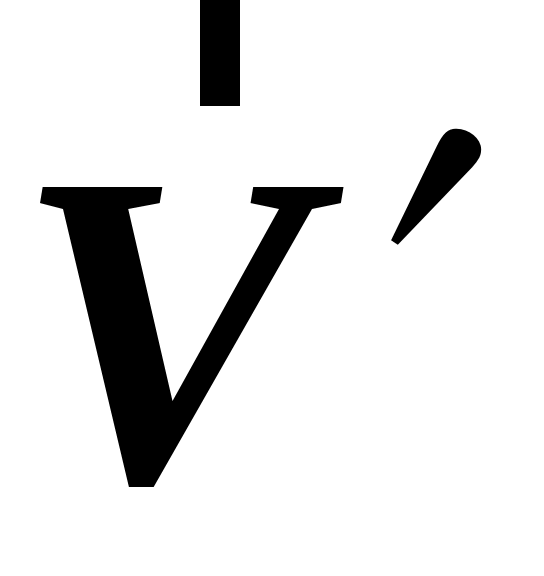 ) в ) в  и и  системах связаны соотношением: системах связаны соотношением:
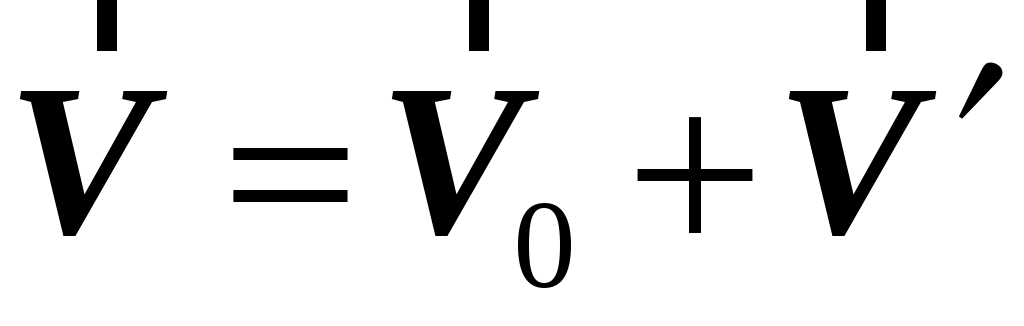 , (1.43) , (1.43)
где 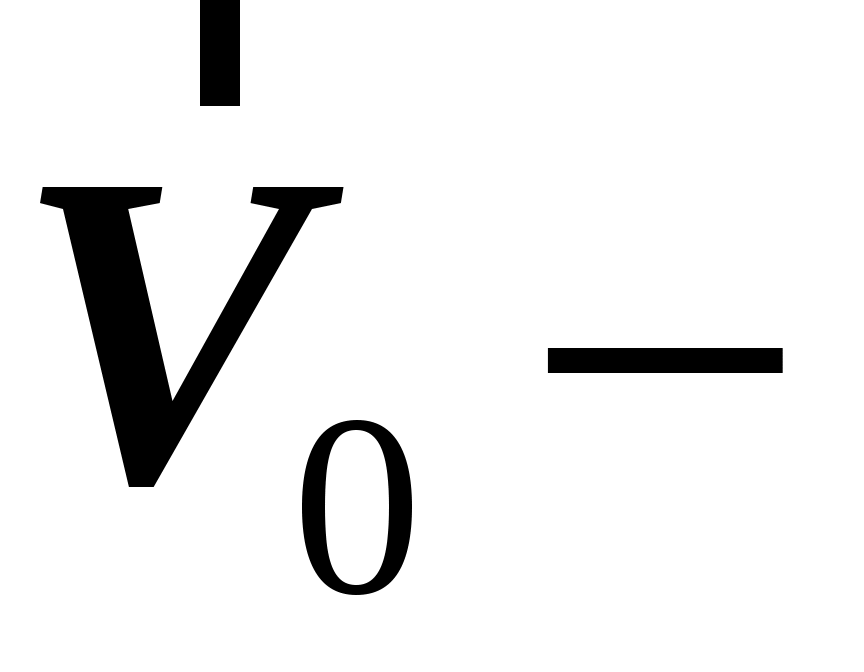 скорость скорость  системы относительно системы относительно 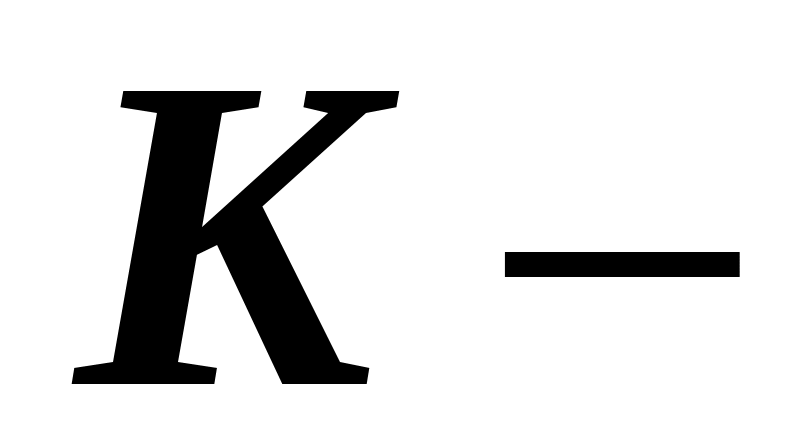 системы. системы.
Для ускорений имеем равенство:
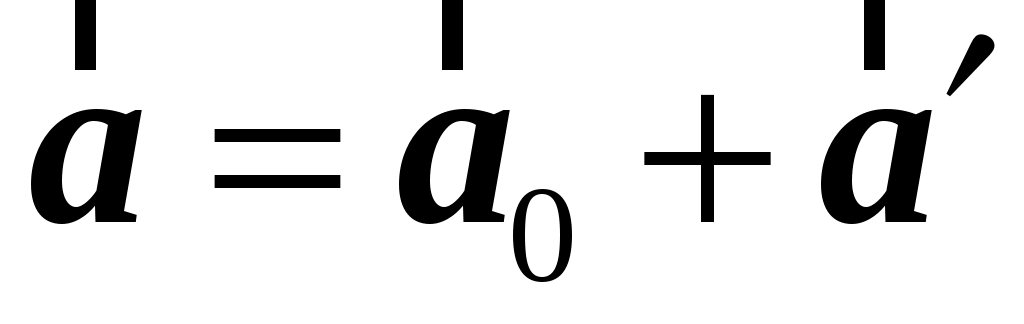 , (1.44) , (1.44)
где 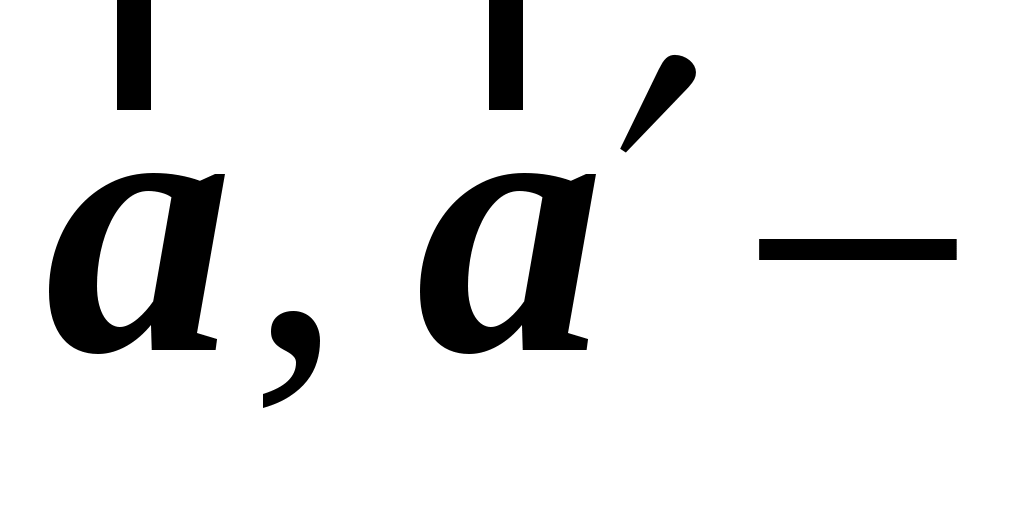 ускорение точки ускорение точки  в в  и и  системах соответственно, системах соответственно, 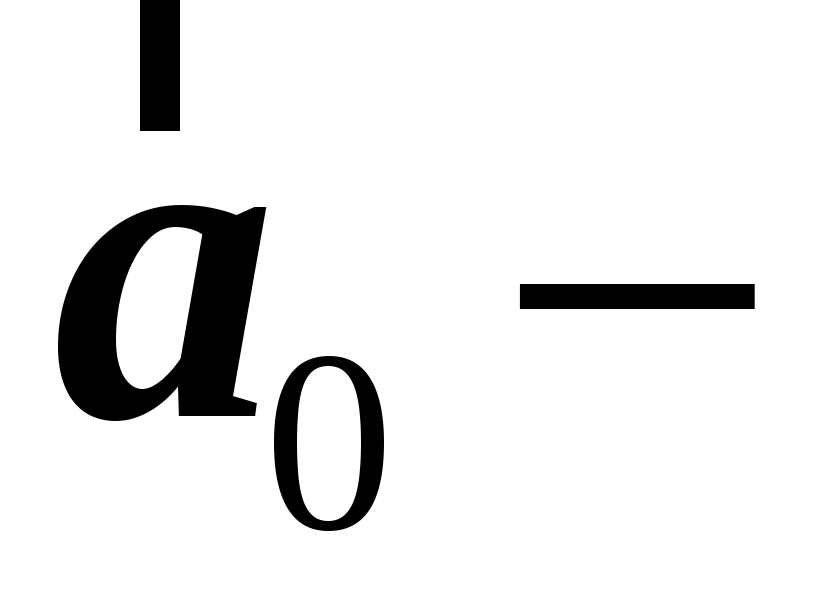 ускорение ускорение  системы относительно системы относительно 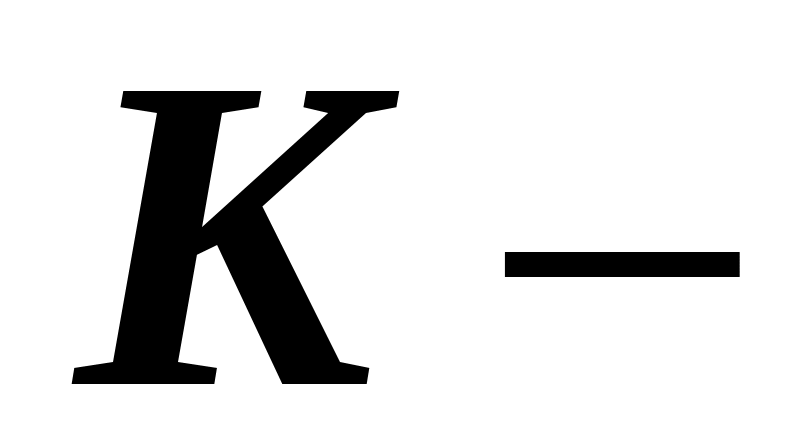 системы. системы.
Из соотношений (1.42)––(1.44) следует, что в перемещение, скорость и ускорение точки  зависит от выбора системы отсчета, т.е. не являются инвариантными величинами для различных систем отсчета. зависит от выбора системы отсчета, т.е. не являются инвариантными величинами для различных систем отсчета.
В том случае, когда  система движется поступательно с постоянной скоростью ( система движется поступательно с постоянной скоростью (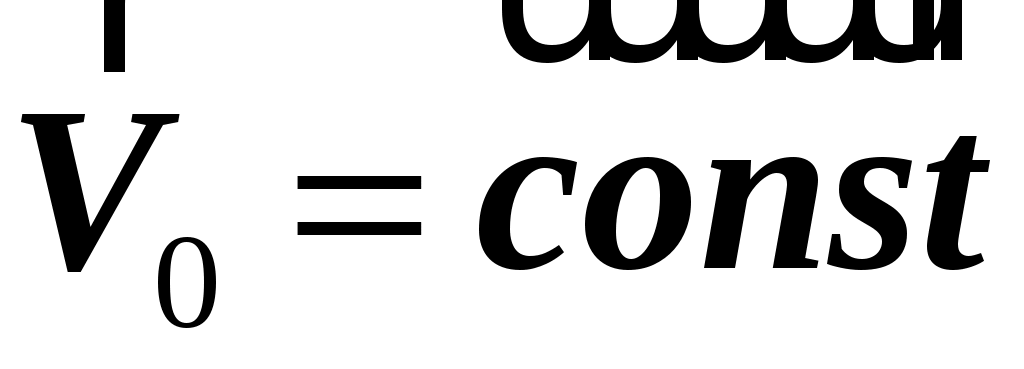 ), ее ускорение ), ее ускорение 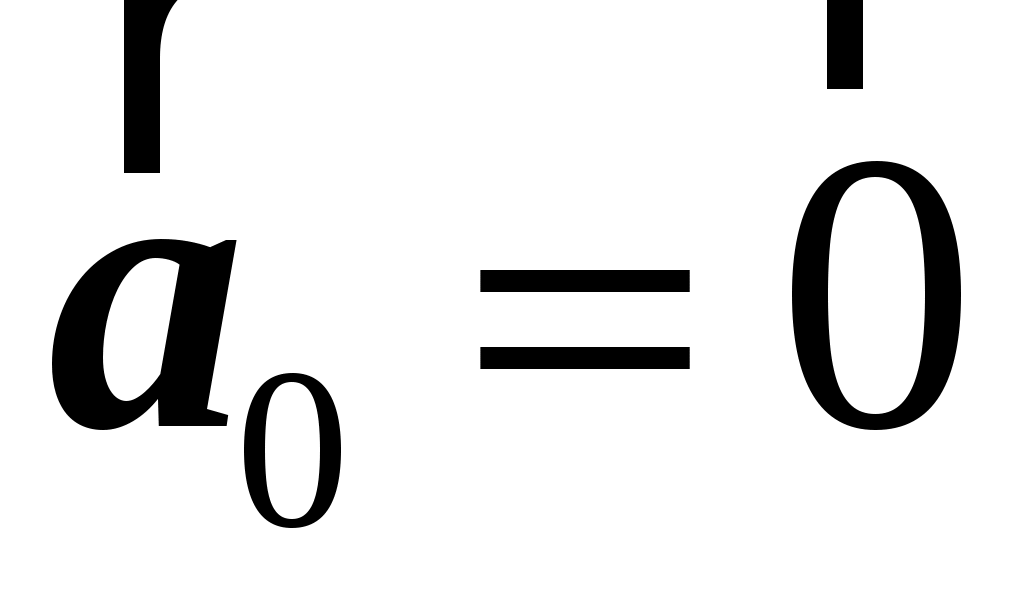 , и, следовательно, имеем равенство: , и, следовательно, имеем равенство:
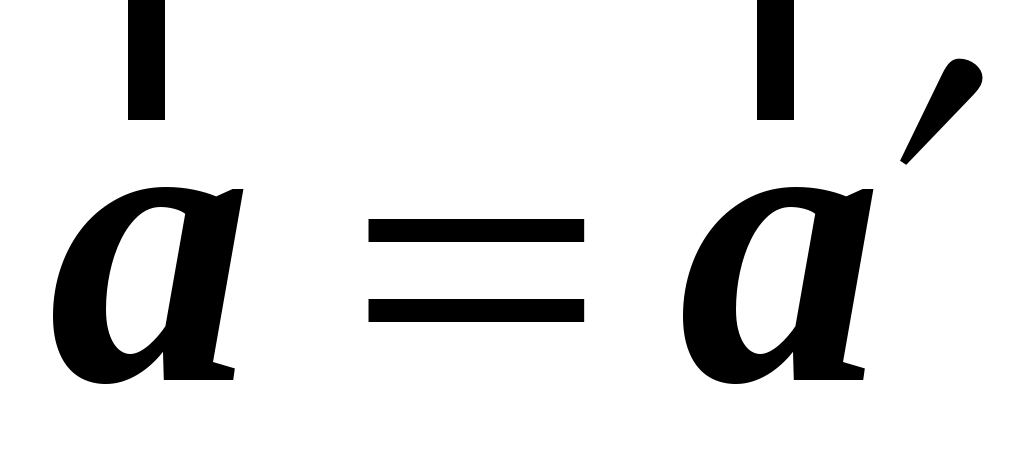 . (1.45) . (1.45)
В этом случае ускорением точки  постоянно в постоянно в  и и  системах. Это означает то, что в инерциальных системах1 отсчета ускорение является инвариантной величиной. системах. Это означает то, что в инерциальных системах1 отсчета ускорение является инвариантной величиной.
2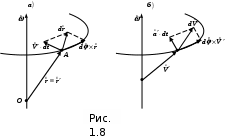
. система вращается с постоянной угловой скоростью система вращается с постоянной угловой скоростью  вокруг оси, неподвижной в вокруг оси, неподвижной в 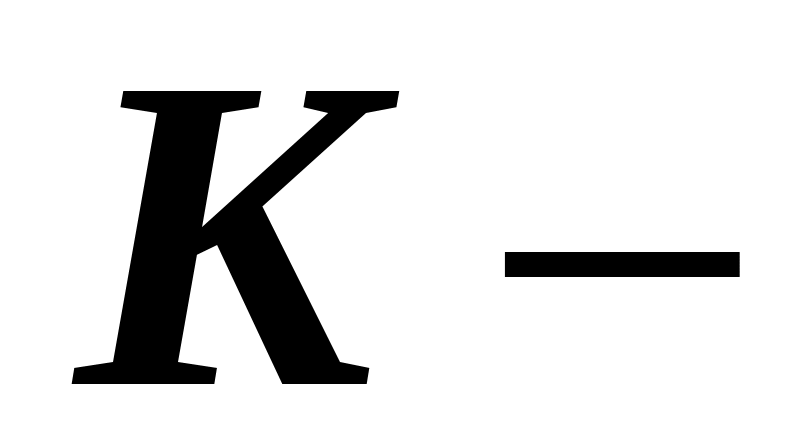 системе.2 Совместим системе.2 Совместим  и и  системы, начало отсчета возьмем на оси вращения. В этом случае в начальный момент времени радиус–вектор точки системы, начало отсчета возьмем на оси вращения. В этом случае в начальный момент времени радиус–вектор точки  можно выбрать одинаковым в можно выбрать одинаковым в  и и  системах ( системах (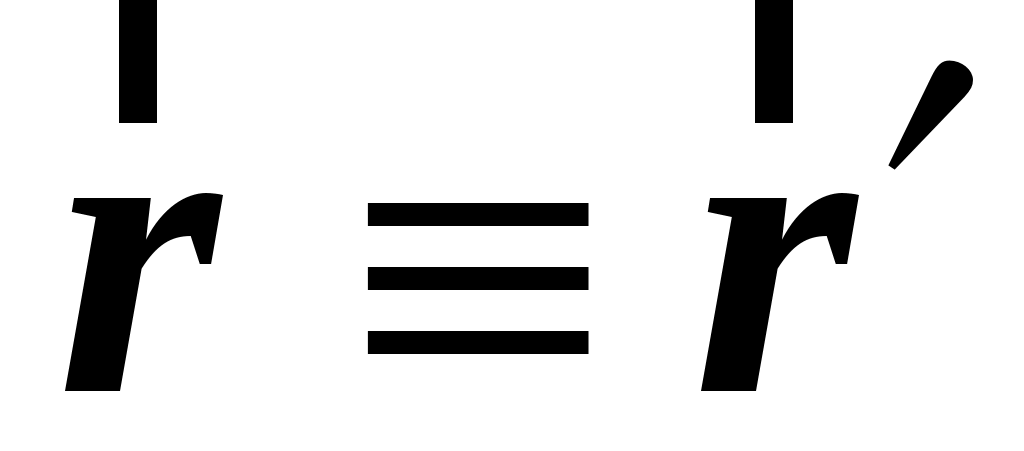 ). Пусть ). Пусть 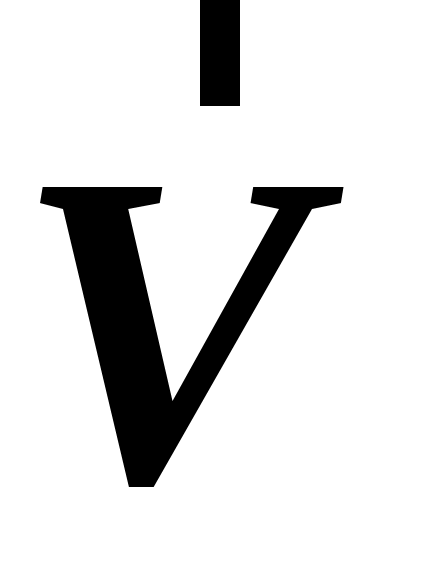 и и 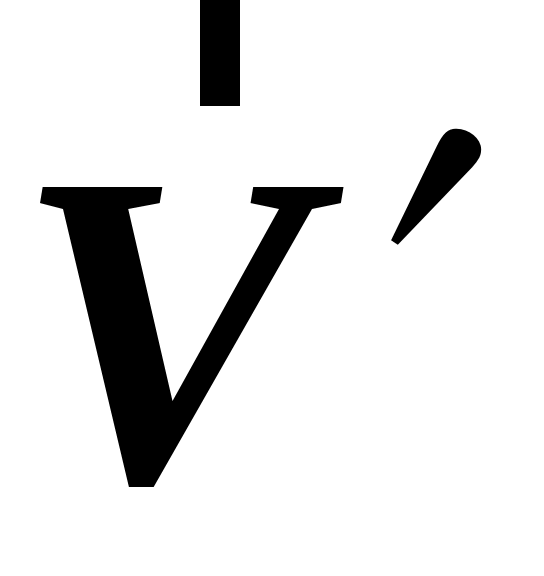 скорости точки скорости точки  в в  и и  системах, тогда перемещение этой точки в системах, тогда перемещение этой точки в  системе равно системе равно 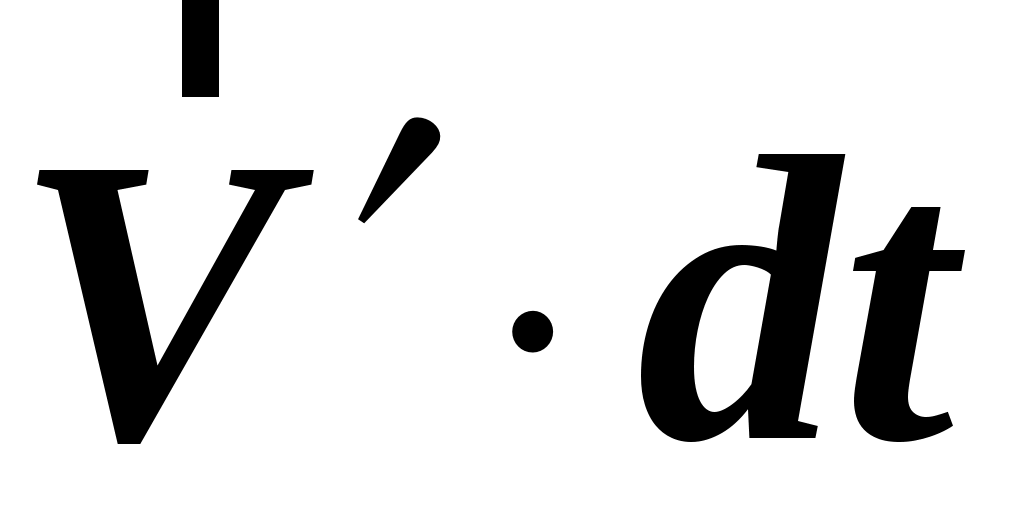 , а перемещение , а перемещение  системы относительно системы относительно  –– –– 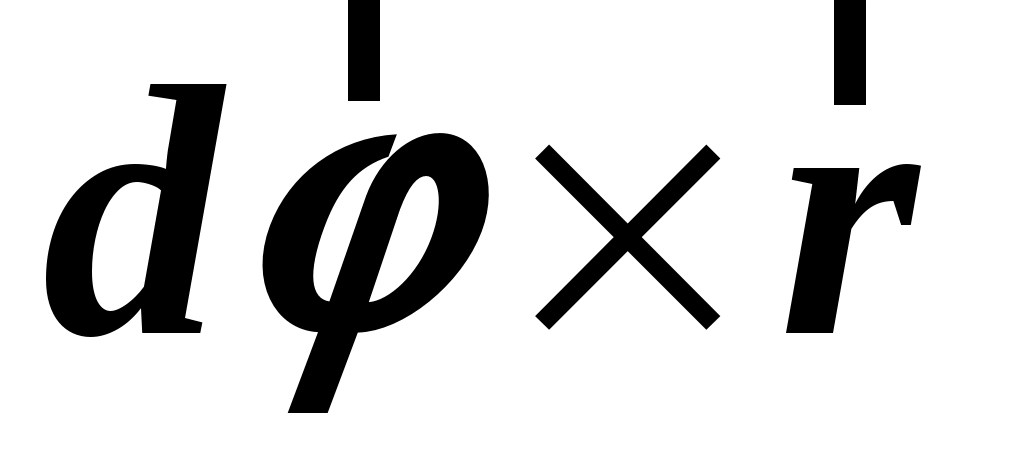 (см. рис. 1.8). При этом угол поворота (см. рис. 1.8). При этом угол поворота  системы за время системы за время  равен равен 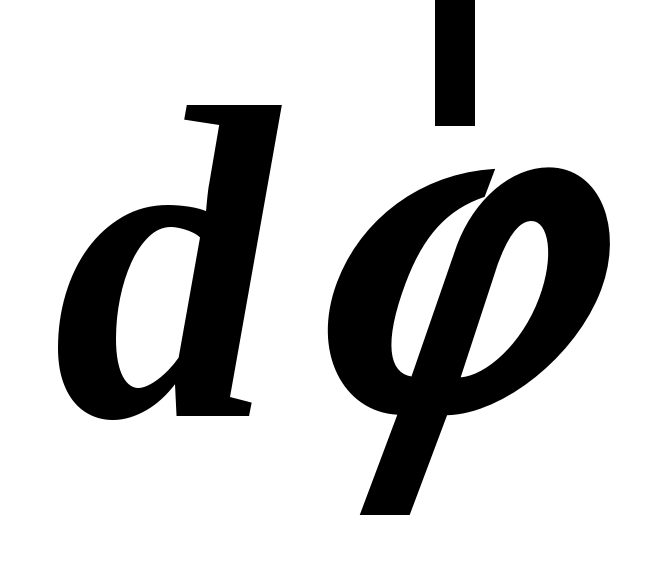 . .
Перемещение точки  в в 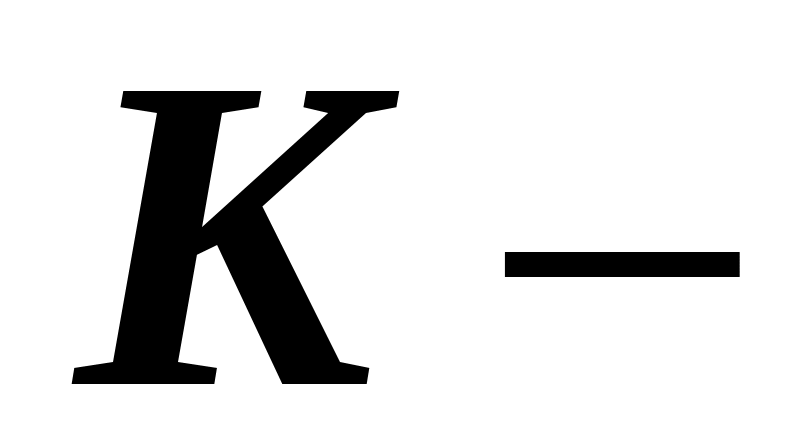 системе равно системе равно
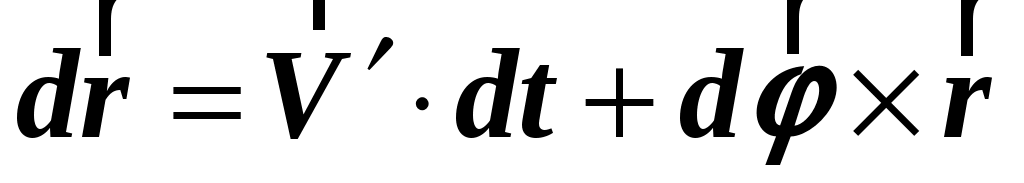 . (1.46) . (1.46)
Соотношение для скоростей 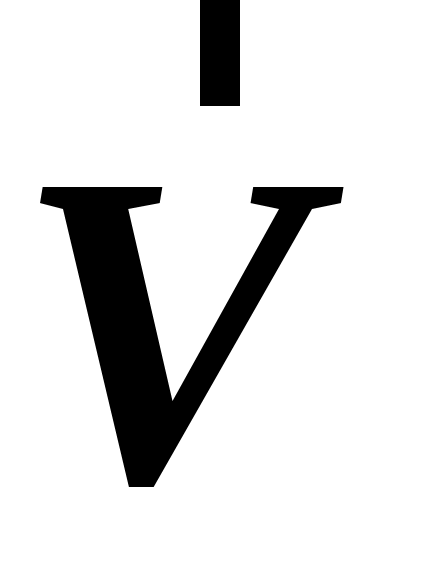 и и 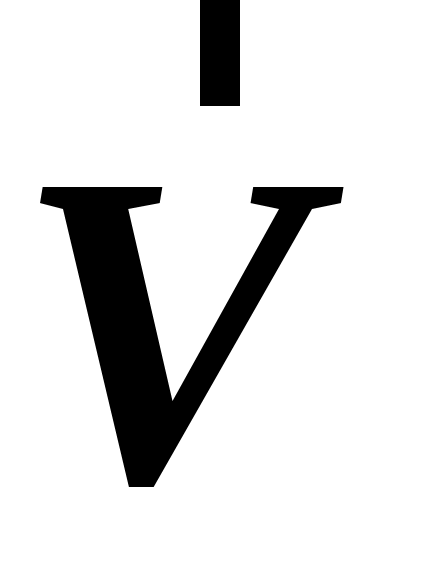 в в  и и  системах имеет вид системах имеет вид
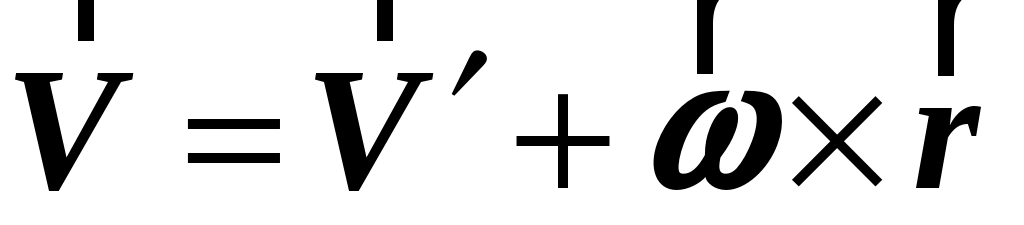 . (1.47) . (1.47)
Ускорения 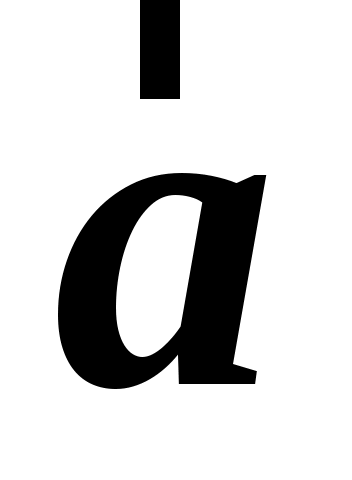 и и 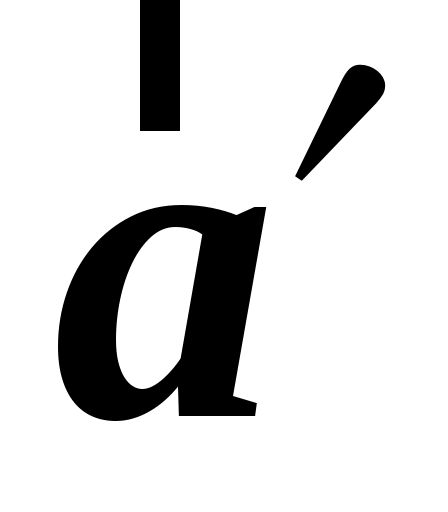 в в  и и  системах связаны соотношением: системах связаны соотношением:
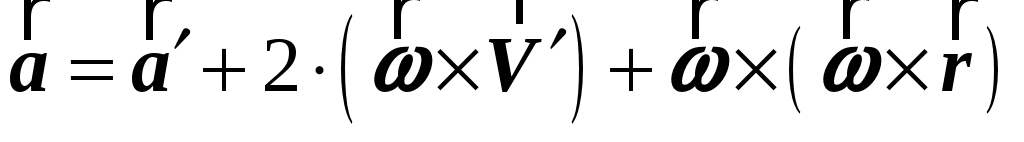 . (1.48) . (1.48)
Второе слагаемое в равенстве (1.48) называют кориолисовым ускорением, а третье слагаемое –– осестремительным ускорением:
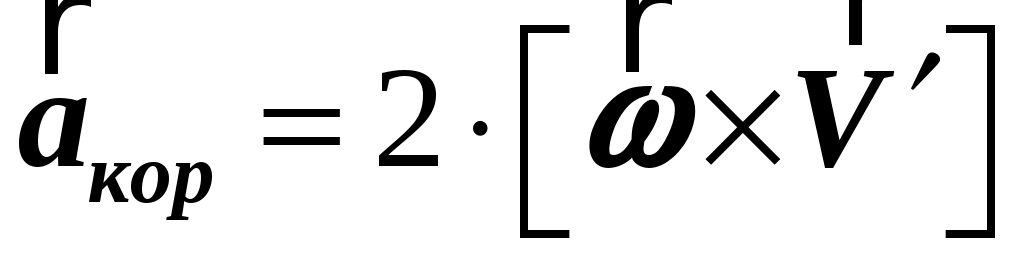 , , 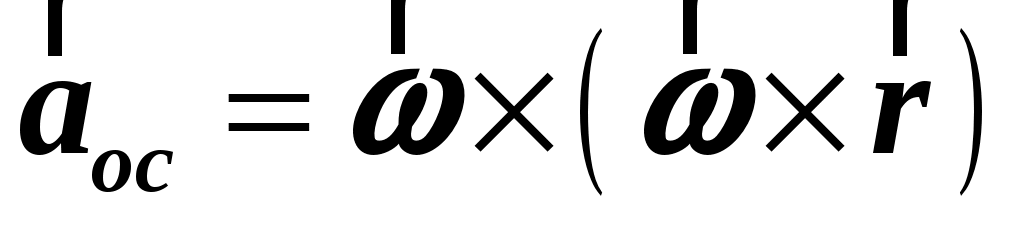 . (1.49) . (1.49)
Пусть 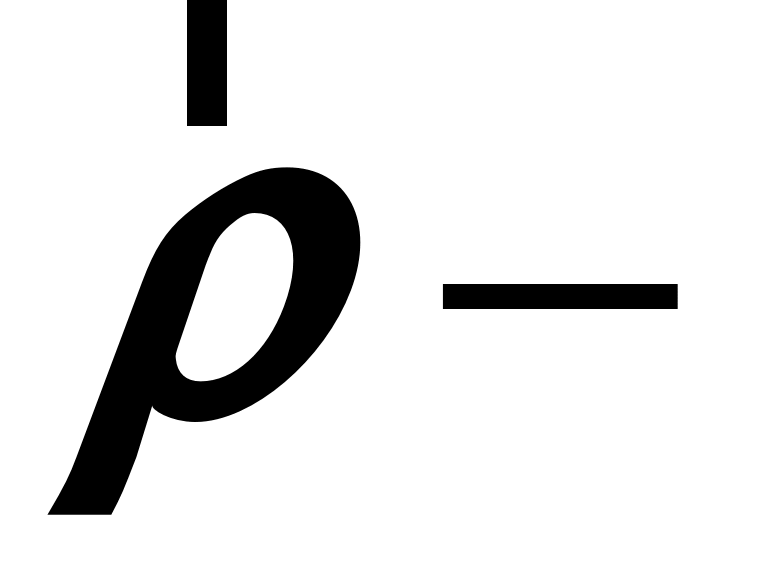 вектор, проведенный в точку вектор, проведенный в точку  перпендикулярно оси вращения, тогда равенство (1.48) примет вид перпендикулярно оси вращения, тогда равенство (1.48) примет вид
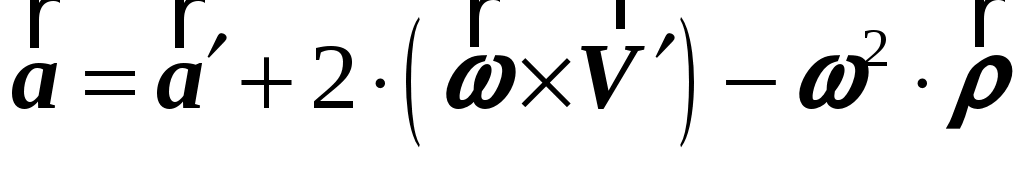 . (1.50) . (1.50)
Для определения направления вектора 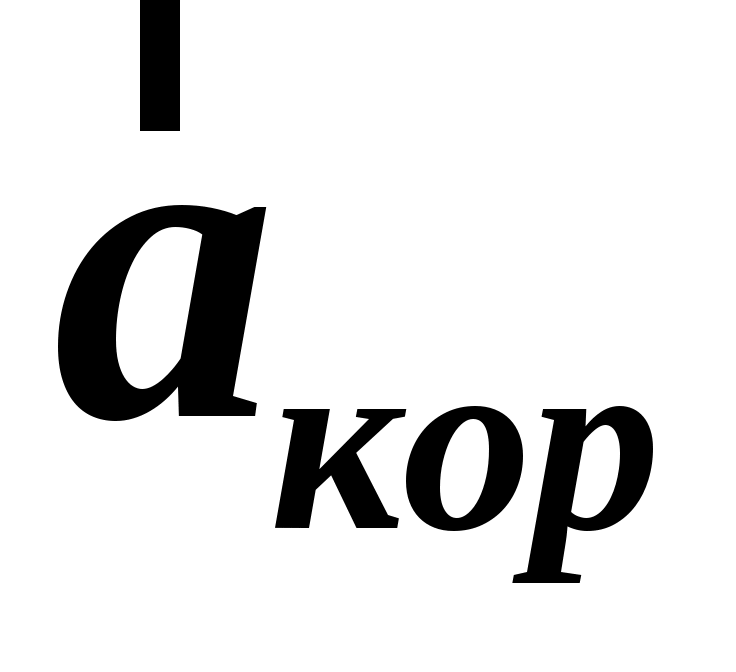 используют равенство (1.49) и правило буравчика, осестремительное ускорение направлено против вектора используют равенство (1.49) и правило буравчика, осестремительное ускорение направлено против вектора 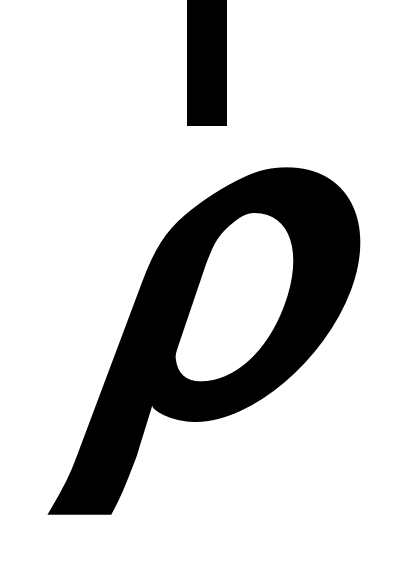 к оси вращения к оси вращения  системы. системы.
 система вращается с постоянной угловой скоростью система вращается с постоянной угловой скоростью  вокруг оси, перемещающейся поступательно со скоростью вокруг оси, перемещающейся поступательно со скоростью 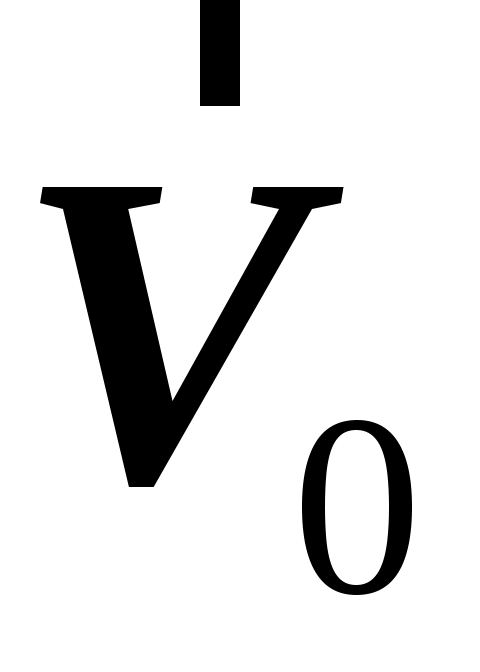 относительно относительно 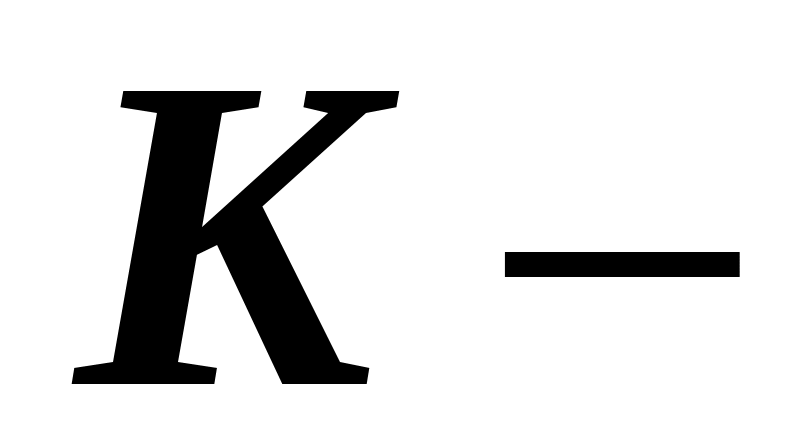 системы.3 системы.3
Пусть 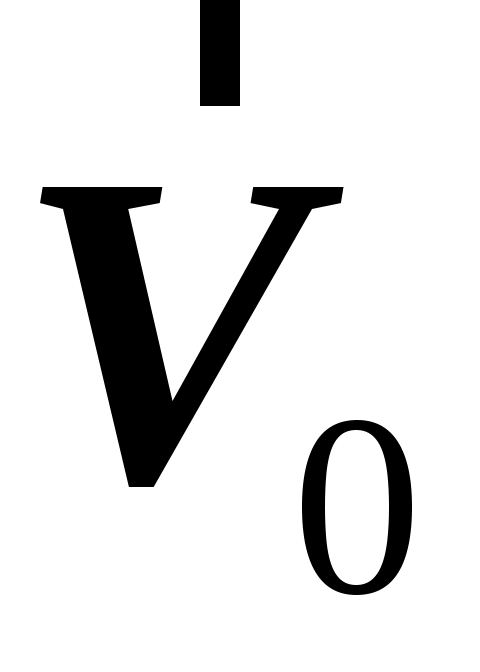 скорость поступательного движения точки скорость поступательного движения точки 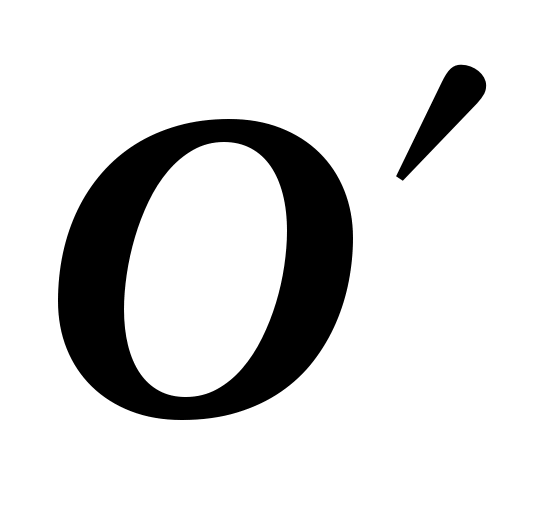 , являющейся точкой отсчета , являющейся точкой отсчета  системы, а системы, а  вектор угловой скорости вращения вектор угловой скорости вращения  системы. Этот случай объединяет два предыдущих. системы. Этот случай объединяет два предыдущих.
Для векторов скорости 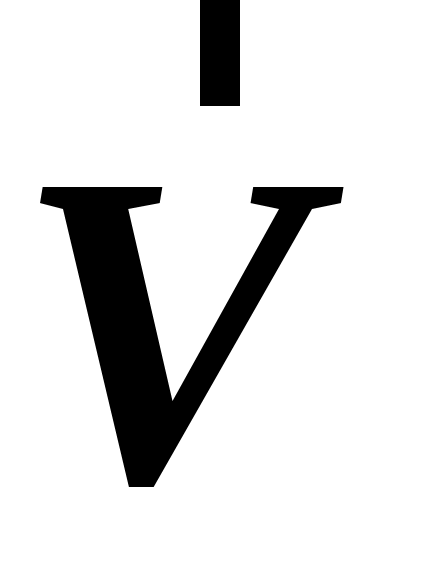 и и 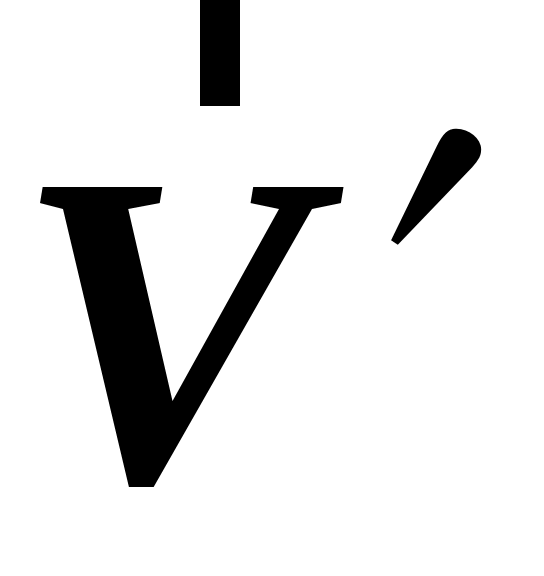 точки в точки в  и и  системах справедлива формула: системах справедлива формула:
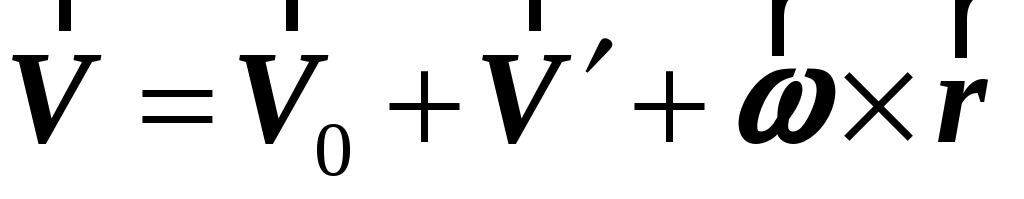 . .
Ускорения точки  в в  и и  системах ( системах (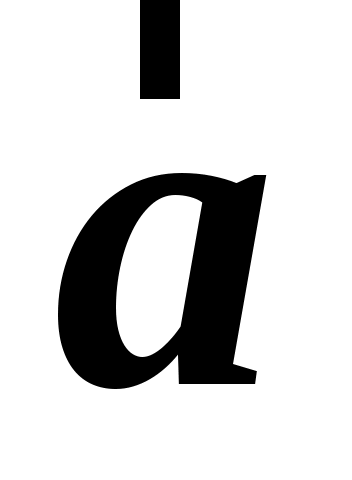 , ,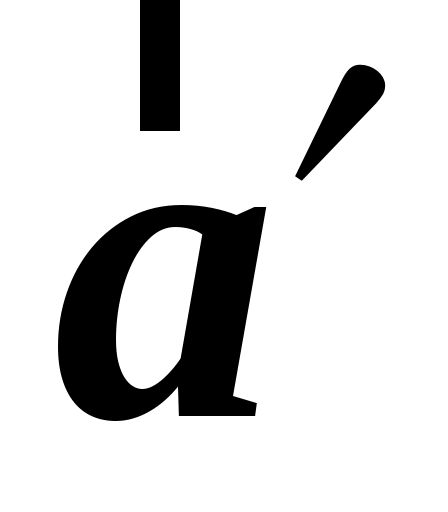 ) удовлетворяют следующему соотношению: ) удовлетворяют следующему соотношению:
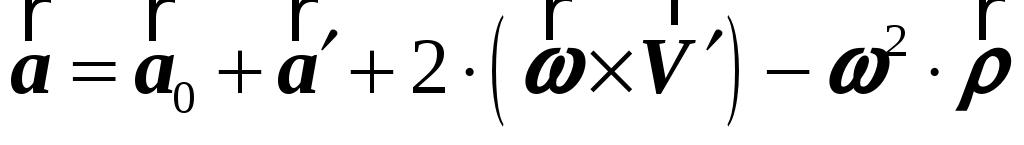 . .
Сила и масса. Принцип суперпозиции сил.



Инерциальная система отсчета и ее связь со свойствами симметрии пространства и времени. Принцип относительности и преобразования Галилея.




Основные законы динамики (законы Ньютона) и границы их применимости.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Первый закон Ньютона утверждает существование инерциальных систем отсчета.
Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач пренебрежимо малы, и в этих случаях ее можно считать инерциальной.
Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, т. е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы).
Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения).
Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:
aF (m=const). (6.1)
При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно:
а
1/т (F=const). (6.2)
Используя выражения (6.1) и (6.2) и учитывая, что сила и ускорение — величины векторные, можем записать
a = kF/m. (6.3)
Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
В СИ коэффициент пропорциональности k= 1. Тогда
a = F/m,
или
F = ma = mdv/dt (6.4)
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:
F=(d/dt)(mv). (6.5)
Векторная величина
p = mv, (6.6)
численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.
Подставляя (6.6) в (6.5), получим
F=dp/dt(6.7)
Это выражение — более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки.
Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы:
1 Н=1 кг•м/с2.
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (6.7).
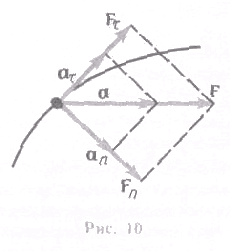
о механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис. 10 действующая сила F = maразложена на два компонента: тангенциальную силу F(направлена по касательной к траектории) и нормальную силу Fn (направлена по нормали к центру кривизны). Используя выражения
а=dv/dt и аn=v2/R, а также v=R, можно записать:
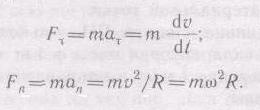
Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под Fво втором законе Ньютона понимают результирующую силу.
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдольпрямой, соединяющей эти точки:
F12=-F2I, (7.1)
где F12— сила, действующая на первую материальную точку со стороны второй; F21— сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
При использовании законов динамики иногда допускают следующую ошибку: так как действующая сила всегда вызывает равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая должна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под действием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий же закон Ньютона говорит о равенстве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Работа силы и потенциальная энергия частицы во внешнем силовом поле. Пример центрально-симметричного поля.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них,— консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией II. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
dA=-dП. (12.2)
Работа dА выражается как скалярное произведение силы Fна перемещение drи выражение (12.2) можно записать в виде
Fdr=-dП. (12.3)
Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу Fпо модулю и направлению.
Потенциальная энергия может быть определена исходя из (12.3) как
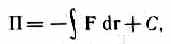
где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил
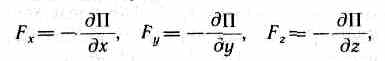
или в векторном виде
F=-gradП, (12.4) где
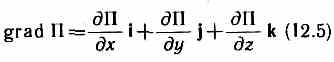
(i, j, k— единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.
Для него наряду с обозначением gradП применяется также обозначение П. («набла») означает символический вектор, называемый оператором Гамильтона4или набла-оператором:
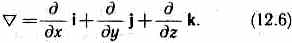
Конкретный вид функции П зависит от характера силового поля.


Закон сохранения и закон изменения механической энергии. Теорема о кинетической энергии.
Закон сохранения импульса для замкнутой системы и теорема об изменении импульса для незамкнутых систем.
Закон сохранения момента импульса для замкнутой системы и теорема об изменении момента импульса для незамкнутых систем.
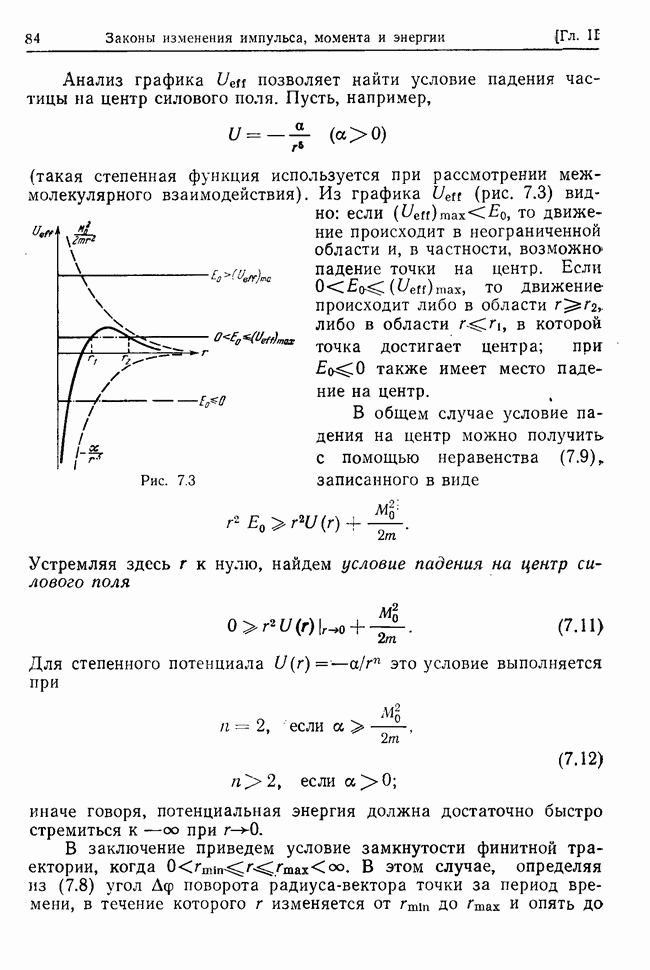
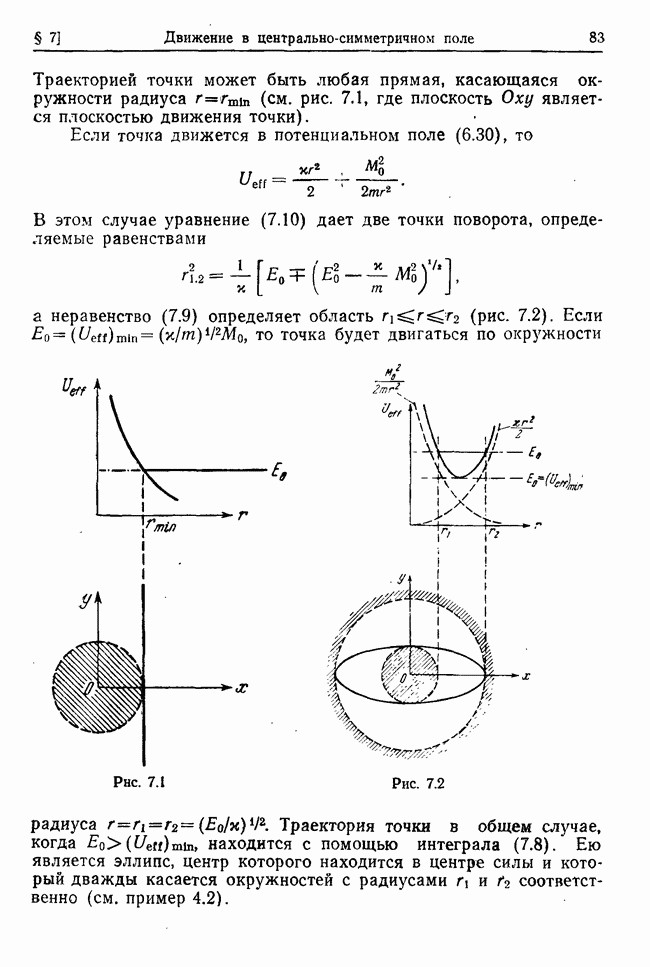
Задача об одномерном движении частиц. Период одномерного финитного движения.
Задача двух тел, ее сведение к одночастичной задаче. Приведенная масса.
Движение частицы в центрально-симметричном поле (общее решение задачи).
Движение частицы в кулоновом поле. Законы Кеплера.
Предпосылки к созданию СТО. Опыт Майкельсона и попытки его истолкования в рамках классической механики.
Постулаты Эйнштейна. Предельная скорость распространения взаимодействий.
Интервал между событиями. Инвариантность интервала.
Преобразования Лоренца и их кинематические следствия.
Релятивистская динамика частицы. Взаимосвязь массы и энергии.
Электрический заряд и электромагнитное поле. Электрический заряд, его свойства. Плотность заряда и плотность тока. Закон сохранения заряда в интегральной и дифференциальной формах.
Электромагнитное поле, его действие на заряды, токи. Напряженность электрического поля, индукция магнитного поля, принцип суперпозиции. Относительность разбиения электромагнитного поля на электрическое и магнитное поля.
Уравнения электромагнитного поля как обобщение опытных факторов. Закон Кулона. Теорема Гаусса — Остроградского в интегральной и дифференциальной формах. Вектор электрической индукции в однородном диэлектрике.
Закон Био — Савара для стационарного магнитного поля в интегральной и дифференциальной формах. Обобщение этого закона на случай переменных полей, учет закона сохранения заряда.
Закон электромагнитной индукции в интегральной и дифференциальной формах. Факт отсутствия магнитных зарядов.
Законы Ома и Джоуля — Ленца в интегральной и дифференциальной формах. Материальные уравнения. Физический смысл всех уравнений Максвелла.
Плотность энергии и плотность потока энергии электромагнитного поля. Закон сохранения энергии в системе частицы — поле. Импульс электромагнитного поля.
Электростатическое поле в диэлектриках. Граничные условия для векторов Е и 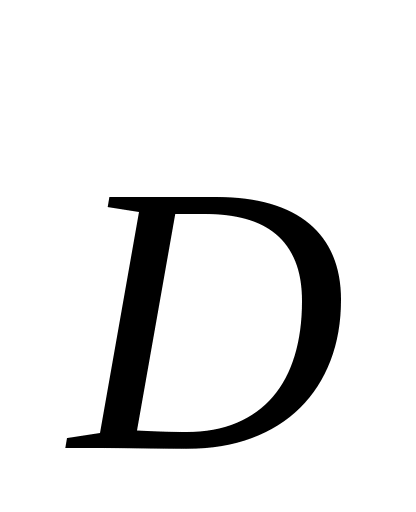 . .
Электростатическое поле в проводниках.
Энергия системы покоящихся зарядов. Плотность энергии электростатического поля (понятие о собственной энергии зарядов). Система зарядов во внешнем поле (энергия, сила, момент силы).
Сторонние электродвижущие силы. Обобщение законов Ома и Джоуля — Ленца.
Уравнения Максвелла для стационарного магнитного поля. Вихревой характер магнитного поля. Векторный потенциал. Уравнение Пуассона для векторного потенциала и его решение. Векторный потенциал системы токов на больших расстояниях в магнитно-дипольном приближении. Магнитный момент и его свойства. Магнитный момент витка с током.
Магнитное поле в магнетиках. Граничные условия для векторов 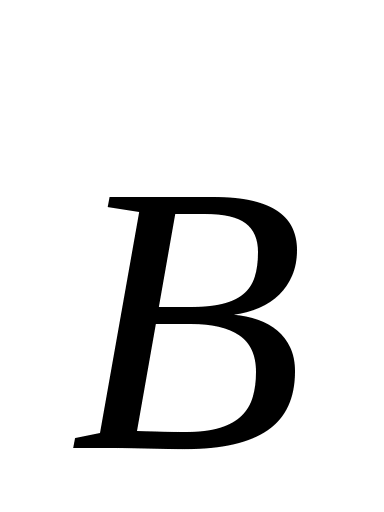 и и 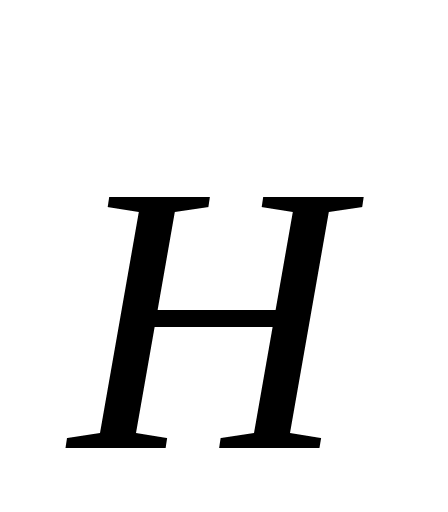 . .
Волновое уравнение. Электромагнитные волны, скорость их распространения. Плоские электромагнитные волны, их характеристики. Свойства плоских монохроматических волн в однородном диэлектрике (поляризация, соотношение между амплитудами, вектор Умова — Пойнтинга). Отражение и преломление электромагнитных волн на границе раздела двух диэлектриков. Электромагнитные зоны в проводящих средах.
Потенциалы электромагнитного поля как переменные его состояния. Калибровочная инвариантность, условие Лоренца. Уравнение для потенциалов.
Излучение электромагнитных волн. Интенсивность излучения гармонического осциллятора. Излучение ускоренно движущегося заряда.
Диэлектрическая восприимчивость полярных и неполярных диэлектриков. Диэлектрики в переменных полях. Классическая теория дисперсии.
1 Относительное движение инерциальных систем всегда прямолинейное и равномерное
2 Материал для дополнительного изучения
3
4
|
 Скачать 1.66 Mb.
Скачать 1.66 Mb.

 чевидно что, векторы
чевидно что, векторы