Паршин задача. Рассчитать среднее время движения маятника можно по формуле можно рассчитать момент инерции маятника
 Скачать 33.23 Kb.
|
|
Рассчитать среднее время движения маятника можно по формуле:    можно рассчитать момент инерции маятника  :   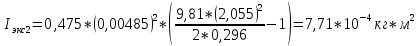Вычислить абсолютную ошибку времени, абсолютную и относительную ошибки момента инерции можно по формулам:  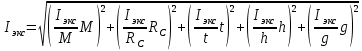  3.3.1. Сначала вычислю абсолютную погрешность времени. 3.3.1.1. Погрешность прибора можно определить по цене деления. Так как прибор измеряет время с точностью до 1 мс, то  .3.3.1.2. Случайная погрешность определяется по формуле:  где  – коэффициент Стьюдента, S - средняя квадратичная погрешность среднего арифметического.Следовательно, перед началом вычислений надо найти недостающие величины. 3.3.1.2.1. Коэффициент Стьюдента (  ) равен 2,9 при α=0,9 и n=3, равен 2,1 при α=0,9 и n=5.3.3.1.2.2. S вычисляется по формуле:  Δ  вычисляется по формуле:Δ  ,следовательно: Δ  Δ 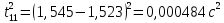 Δ  Δ   Δ  Δ  Δ  Δ  Δ   Теперь можно вычислить  :  Абсолютная погрешность равна:   Теперь вычислю абсолютную погрешность момента инерции. Так как g – табличная величина, то в качестве абсолютной погрешности принимается половина разряда последней значащей цифры числа, т.е.  .        Для упр. 2:   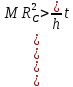   3.3.3. Теперь вычислю относительную погрешность момента инерции.   3.4. По формуле (7) можно рассчитать теоретический момент инерции маятника  :    3.5. Сравниваю экспериментальное и теоретическое значения момента инерции, вычислив разницу между ними в процентах:   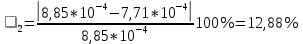 3.6. На основе полученных экспериментальных значений рассчитаю момент инерции кольца  по формуле (6): откуда  Так как значение  получено в ходе эксперимента с использованием кольца, стержня и диска, то его значение можно принять как I, и так как  получено с использованием стержня и диска, но без кольца, то его значение можно принять как  :  3.7. На основе полученных теоретический значений рассчитаю момент инерции кольца по формуле:  3.8. Сравниваю экспериментальное и теоретическое значения момента инерции кольца, вычислив разницу между ними в процентах:   Заключение Определил момент инерции маятника Максвелла. Для этого рассчитал теоретические значения инерции и провел опыты, чтобы рассчитать экспериментальные значения:     Также вычислил теоретическое и экспериментальное значение инерции кольца:  – экспериментальное – теоретическое |