Решение. 0,9 1 0,9 0,1 5 2
 Скачать 34.48 Kb. Скачать 34.48 Kb.
|
Вариант 1.Найти вероятность того, что среди взятых наудачу пяти деталей две стандартные, если вероятность того, что каждая деталь окажется стандартной, равна 0,9. Решение. 𝑝 = 0,9; 𝑞 = 1 − 0,9 = 0,1 𝑛 = 5; 𝑘 = 2 Искомую вероятность найдем по формуле Бернулли: 𝑛 𝑃𝑛(𝑘) = 𝐶𝑘𝑝𝑘𝑞𝑛−𝑘.  𝐶𝑘 = 𝑛! 𝑛 𝑃 = 𝑃 (2) = 𝐶2 · 𝑝2 · 𝑞3 = 5! 𝑘! (𝑛 − 𝑘)! · 0,92 · 0,13 = 10 · 0,92 · 0,13 = 0,0081  5 5 2! · 3! Ответ: 0,0081. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами и 2, которые характеризуются следующими законами распределения:
Результаты стрельбы одного стрелка не влияют на результаты стрельбы второго. Составить закон распределения числа очков, выбиваемых данной командой, если стрелки сделают по одному выстрелу. Найдём закон распределения случайной величины = . Заполним расчетную таблицу:
В случае совпадения некоторых сумм соответствующие вероятности складываются: 𝑃(𝑍 = 5) = 0,02 + 0,03 = 0,05 𝑃(𝑍 = 6) = 0,02 + 0,03 + 0,05 = 0,10 𝑃(𝑍 = 7) = 0,04 + 0,03 + 0,05 = 0,12 𝑃(𝑍 = 8) = 0,10 + 0,06 + 0,05 = 0,21 𝑃(𝑍 = 9) = 0,15 + 0,10 = 0,25 Таким образом, закон распределения случайной величины 𝑍 = X + 𝑌 примет вид:
Убеждаемся в том, что сумма вероятностей всех возможных исходов равна единице. Действительно, ∑ 𝑝i = 0,02 + 0,05 + 0,10 + 0,12 + 0,21 + 0,25 + 0,25 = 1 Ответ:
Вариант 2.В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, и для третьей – 4%. Чему равна вероятность того, что оказавшееся нестандартным изделие произведено на ПЕРВОЙ фабрике? Решение. 𝐻1 − продукция поступила с первой фабрики. 𝑃(𝐻1 ) = 20  100 100= 0,2 𝐻2 − продукция поступила со второй фабрики. 𝑃(𝐻2 ) = 45  100 100= 0,45 𝐻3 − продукция поступила с третьей фабрики. 𝑃(𝐻3 ) = 35  100 100= 0,35 𝐴 − изделие оказалось нестандартным. Условные вероятности этого события равны: 𝑃𝐻1 (𝐴) = 0,03; 𝑃𝐻2 (𝐴) = 0,02; 𝑃𝐻3 (𝐴) = 0,04 По формуле полной вероятности имеем: 𝑃(𝐴) = ∑𝑃(𝐻i) · 𝑃𝐻i(𝐴); 𝑃(𝐴) = 0,2 * 0,03 + 0,45 * 0,02 + 0,35 * 0,04 = 0,029 Вероятность того, что оказавшееся нестандартным изделие произведено на первой фабрике, найдем по формуле Байеса:  𝑃 (𝐻 ) = 𝑃(𝐻i) * 𝑃𝐻i(𝐴) 𝐴 i 𝑃(𝐴) 𝑃 (𝐻 ) = 𝑃(𝐻1) * 𝑃𝐻1 (𝐴) = 0,2 * 0,03 ≈ 0,2069   𝐴 1 𝑃(𝐴) 0,029 Ответ: 0,2069. Найти дисперсию случайной величины X, имеющей следующий закон распределения
Решение. Математическое ожидание: 𝑀(X) = ∑ 𝑥i𝑝i 𝑀(X) = 1 · 0,1 + 2 · 0,2 + 3 · 0,3 + 4 · 0,3 + 5 · 0,1 = 3,1 Дисперсия: 𝐷(X) = 𝑀(X2) − 𝑀2(X); 𝐷(X) = 12 · 0,1 + 22 · 0,2 + 32 · 0,3 + 42 · 0,3 + 52 · 0,1 − (3,1)2 = 1,29 Ответ: 𝐷(𝑥) = 1,29 Вариант 3.Завод изготовил две партии автомобилей. Первая партия в три раза больше второй. Надежность автомобилей первой партии 0,9, второй 0,8. Определить вероятность того, что наугад купленный автомобиль будет надежным. Решение. Пусть 𝑥 автомобилей изготовлено второй партией, тогда первой партией изготовлено 3𝑥 автомобилей.  𝑥 + 3𝑥 = 1; 4𝑥 = 1; 𝑥 = 1 𝑥 + 3𝑥 = 1; 4𝑥 = 1; 𝑥 = 14 𝐻1 − автомобиль изготовлен первой партией. 𝑃(𝐻1) = 3 4 = 0,75 𝐻2 − автомобиль изготовлен второй партией. 𝑃(𝐻2) = 1 4 = 0,25 𝐴 − купленный автомобиль будет надежным. Условные вероятности этого события равны: 𝑃𝐻1 (𝐴) = 0,9; 𝑃𝐻2 (𝐴) = 0,8 По формуле полной вероятности имеем: 𝑃(𝐴) = ∑𝑃(𝐻i) · 𝑃𝐻i(𝐴); 𝑃(𝐴) = 0,75 * 0,9 + 0,25 * 0,8 = 0,875 Ответ: 0,875. График функции распределения случайной величины имеет вид: 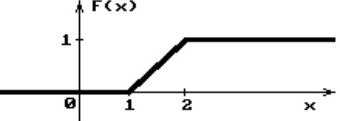 Найти 𝑀(𝑥). Решение. Найдем функцию распределения 𝐹(𝑥). При 𝑥 < 1 𝐹(𝑥) = 0 При 1 ≤ 𝑥 ≤ 2 график проходит через точки (1,0) и (2,1). Уравнение прямой, проходящее через 2 точки (𝑥1; 𝑦1) (𝑥2; 𝑦2), имеет вид: 𝑥 − 𝑥1  𝑥2 − 𝑥1 = 𝑦 − 𝑦1  𝑦2 − 𝑦1 𝑦2 − 𝑦1Подставляя в него координаты точек (1,0) и (2,1), получаем: 𝑥 − 1 = 𝑦 − 0 ; 𝑥 − 1 𝑦     𝑦 = 𝑥 − 1 2 − 1 1 − 0 1 = 1 ; Таким образом, при 1 ≤ 𝑥 ≤ 2 𝐹(𝑥) = 𝑥 − 1 При 𝑥 > 2 𝐹(𝑥) = 1 Функция распределения примет вид: 0 𝑥 < 1 𝐹(𝑥) = {𝑥 − 1 1 ≤ 𝑥 ≤ 2 1 𝑥 > 2 Плотность распределения ƒ(𝑥) = 𝐹 (𝑥):
+∞ 𝑀(𝑥) = ∫ 𝑥ƒ(𝑥)𝑑𝑥 −∞ 1 2 ∞ 1 2 ∞ 𝑀(𝑥) = ∫ 𝑥 · 0 𝑑𝑥 + ∫ 𝑥 · 1 𝑑𝑥 + ∫ 𝑥 · 0 𝑑𝑥 = ∫ 0 𝑑𝑥 + ∫ 𝑥 𝑑𝑥 + ∫ 0 𝑑𝑥 = −∞ 1 2 𝑥2 2 −∞ 1 2   22 12 22 12 = 0 + ( 2 )| = 0 + ( 2 )|1 + 0 = 2 − 2 = 1,5 Ответ: 𝑀(𝑥) = 1,5. Вариант 4.В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? Решение. Применим классическое определение вероятности:  𝑃(𝐴) = 𝑚 𝑃(𝐴) = 𝑚𝑛 𝑚 − число благоприятных исходов; 𝑛 − число всевозможных исходов; Всего имеется 15 шаров (9 белых и 6 черных), из них вынимают два => 𝑛 = 𝐶2 = 15! = 14 * 15 = 105   15 2! * 13! 15 2! * 13!1 * 2 𝐶 = 𝑛! − 𝑛 𝑚  𝑛 𝑚! (𝑛 − 𝑚)! 𝐴 − оба вынутых шара окажутся белыми. 𝑚 = 𝐶0 · 𝐶2 = 6! * 9! = 1 * 36 = 36  6 9 0! * 6!  2! * 7! Ответ: 0,3429. 𝑃(𝐴) = 36  105 105= 12 ≈ 0,3429  35 35В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 1000 руб. и одна стоимостью 3000 руб. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 100 руб.; всего продано 50 билетов. Решение. Случайная величина X − сумма чистого выигрыша, может принимать три значения: - 100 руб. (если студент не выиграет, а фактически проиграет 100 руб., уплаченные им за билет), 900 руб. и 2900 руб. (фактический выигрыш уменьшается на 100 руб. - на стоимость билета). Первому результату благоприятствуют 47 случаев из 50, второму - 2, а третьему - один. Поэтому их вероятности таковы: 𝑝1 (𝑥 = −100) = 47 = 0,94  50 50𝑝2 (𝑥 = 900) = 2  50 50= 0,04 𝑝3 (𝑥 = 2900) = 1  50 50= 0,02 Закон распределения примет вид:
Ответ:
Вариант 5.Завод изготовил две партии телевизоров. Первая партия телевизоров в два раза больше второй. Надежность телевизоров первой партии – 0,9, второй партии – 0,8. Определить вероятность того, что наугад купленный телевизор будет надежным. Решение. Пусть 𝑥 телевизоров изготовлено второй партией, тогда первой партией изготовлено 2𝑥 телевизоров.  𝑥 + 2𝑥 = 1; 3𝑥 = 1; 𝑥 = 1 𝑥 + 2𝑥 = 1; 3𝑥 = 1; 𝑥 = 13 𝐻1 − телевизор изготовлен первой партией. 𝑃(𝐻1) = 2/3 𝐻2 − телевизор изготовлен второй партией. 𝑃(𝐻2) = 1/3 𝐴 − купленный телевизор будет надежным. Условные вероятности этого события равны: 𝑃𝐻1 (𝐴) = 0,9; 𝑃𝐻2 (𝐴) = 0,8 По формуле полной вероятности имеем: 𝑃(𝐴) = ∑𝑃(𝐻i) · 𝑃𝐻i(𝐴); ( ) 2 1 13    𝑃 𝐴 = 3 * 0,9 + 3 * 0,8 = 15 ≈ 0,8667 Ответ: 0,8667. В парке отдыха организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 – по 100 руб.; 300 – по 200 руб.; 200 – по 1000 руб. и 100 – по 2000 руб. Какой средний размер выигрыша для посетителя парка, купившего один билет? Решение. Случайная величина X − размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы: 𝑝1 𝑝2 (𝑥 = 100) = 400  1000 1000 (𝑥 = 200) = 300 (𝑥 = 200) = 3001000 = 0,4 = 0,3 𝑝3 𝑝4 (𝑥 = 1000) = 200  1000 1000 (𝑥 = 2000) = 100 (𝑥 = 2000) = 1001000 = 0,2 = 0,1 Закон распределения примет вид:
Математическое ожидание: 𝑀(X) = ∑ 𝑥i𝑝i 𝑀(X) = 100 · 0,4 + 200 · 0,3 + 1000 · 0,2 + 2000 · 0,1 = 500 Ответ: средний размер выигрыша для посетителя парка, купившего один билет, составит 500 рублей. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 4-е, стер. М.: Высш. шк., 1997. – 400 с.: ил. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 6-е, стер. – М.: Высш. шк., 1997. – 479 с.: ил. Гнеденко Б.В. Курс теории вероятностей: Учебник – Изд. 6-е, перераб. и доп. – М.: Наука. Гл. ред. физ. –мат. лит., 1988. – 448 с. |
