Сопромат. РЕШЕНИЕ_три_момента. Решение. Балка имеет две промежуточных опоры, ссн эквивалентная система представлена на рисунке 2
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
Для стальной балки, изображенной на рисунке 1, дано: 𝑃1 =14 кН, 𝑃2 =14 кН, 𝑞 =26 кН/м , 𝑀1 = 28 кН·м, 𝑀2 = 34 кН·м, 𝑎=3 м, b =2 м, c=1 м, d=1,2 м, e= f =1 м, g=1 м, [𝜎] = 160 МПа, [𝜏]=100 МПа. П 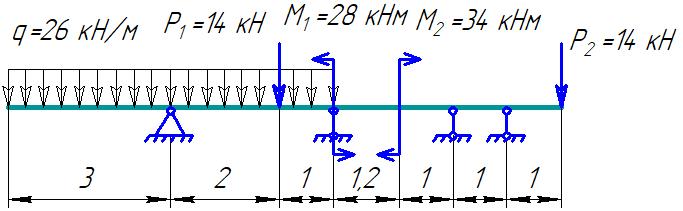 остроить эпюры поперечных сил и изгибающих моментов, изобразить приближенное очертание изогнутой оси балки, подобрать двутавровое поперечное сечение с проверкой по касательным напряжениям. Рис. 1 Решение. 1. Балка имеет две промежуточных опоры, ССН=2. 2. Эквивалентная система представлена на рисунке 2. 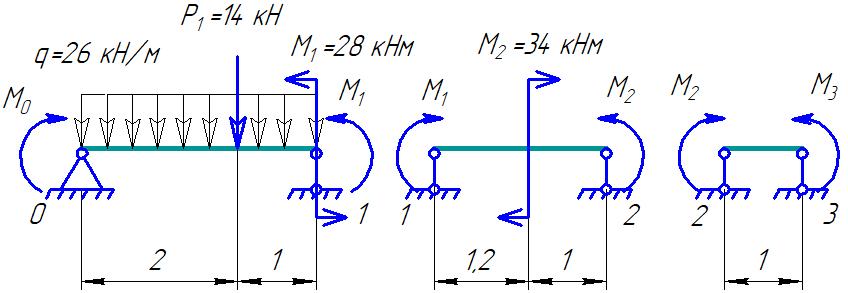 Рис. 2 Составляем уравнения трех моментов для каждых двух соседних пролётов, получаем систему уравнений: 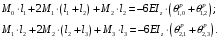 Систему нужно решить относительно моментов на промежуточных опорах, то есть 𝑀1 и 𝑀2. При этом  кНм, кНм, 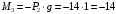 кНм, кНм, 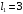 м, м, 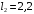 м, м, 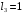 м. м.3 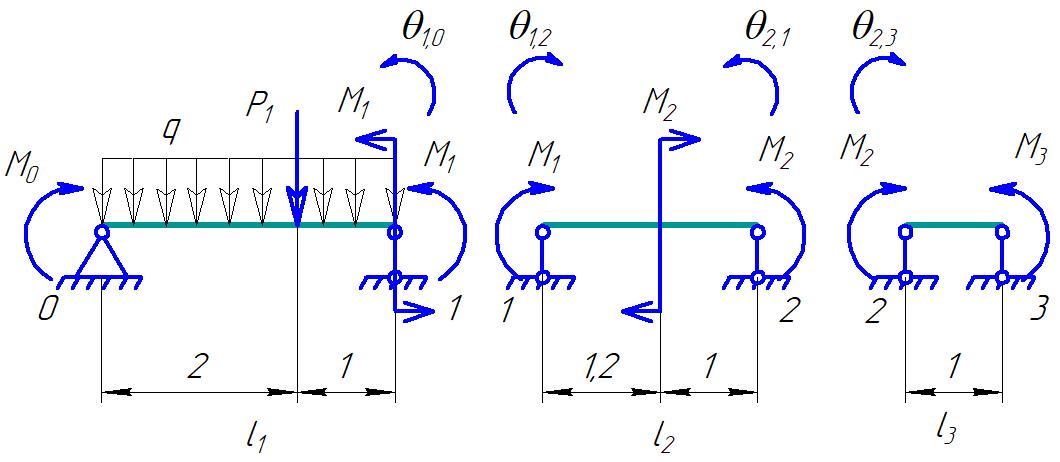 . Для определения углов поворота от внешней нагрузки нужно рассмотреть балки, изображённые на рисунке 3. Рис. 3 3.1. Угол 𝜃1,0 найдем методом начальных параметров. Р 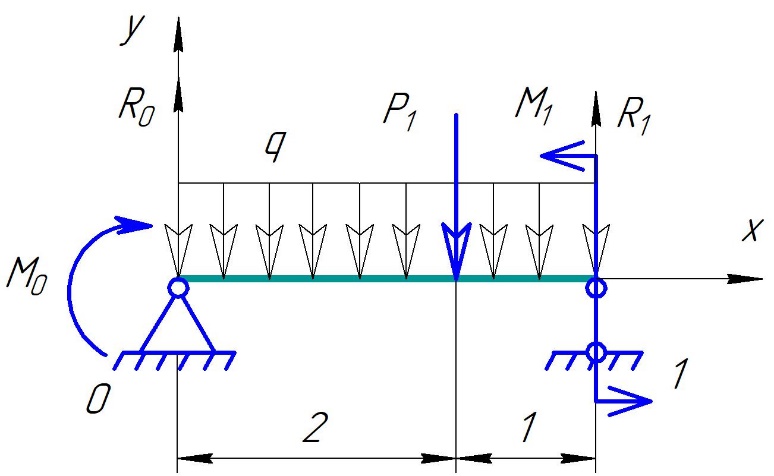 ассмотрим первую балку (рис.4). Рис. 4 Определим реакции опор: 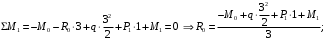 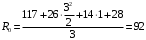 кН; кН;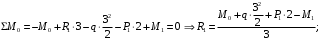 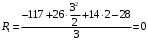 кН. кН.Составим уравнение упругой линии: 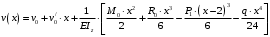 . .Из граничных условий: 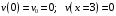 ; ; 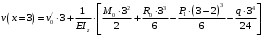 ; ;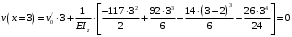 . .Из последнего уравнения находим угол поворота в начале координат:  . .Запишем уравнение углов поворота для первой балки: 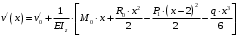 ; ;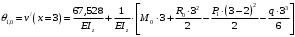 ; ;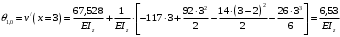 . .3.2. углы 𝜃1,2 и 𝜃2,1 найдем способом Верещагина. Перемножим эпюру от внешней нагрузки (рис. 5 а) с эпюрами от единичных моментов (рис.5 b,c). 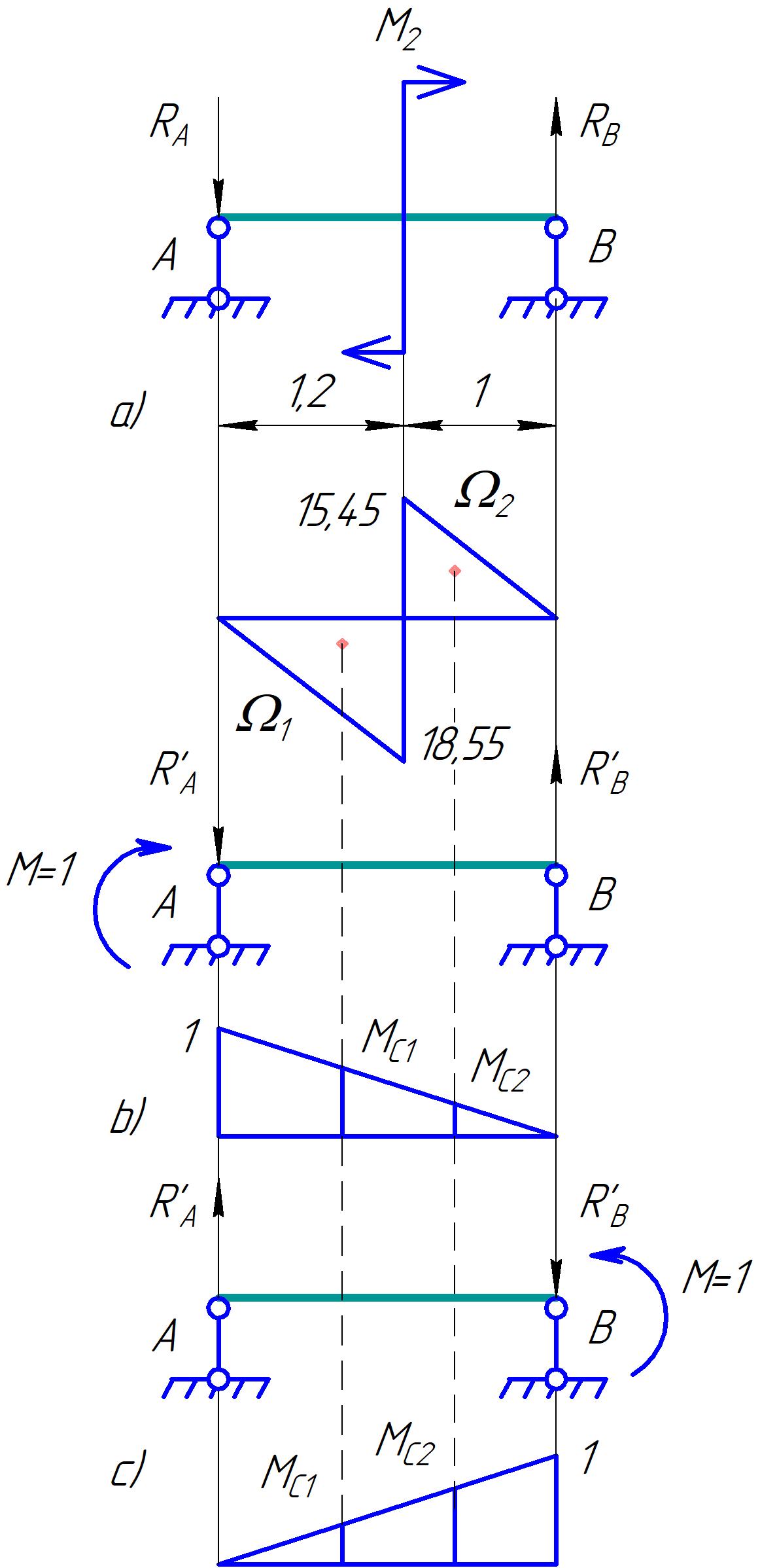 Рис. 5 Найдем площади, ограниченные эпюрами от внешней нагрузки. 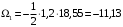 кНм2; кНм2;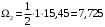 кНм2. кНм2.Ординаты единичных эпюр: На рисунке 5,b 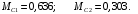 На рисунке 5,c 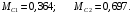 Вычислим углы 𝜃1,2 и 𝜃2,1.  ; ; . .3.3 Для определения угла 𝜃2,3 воспользуемся интегралом Мора. Р 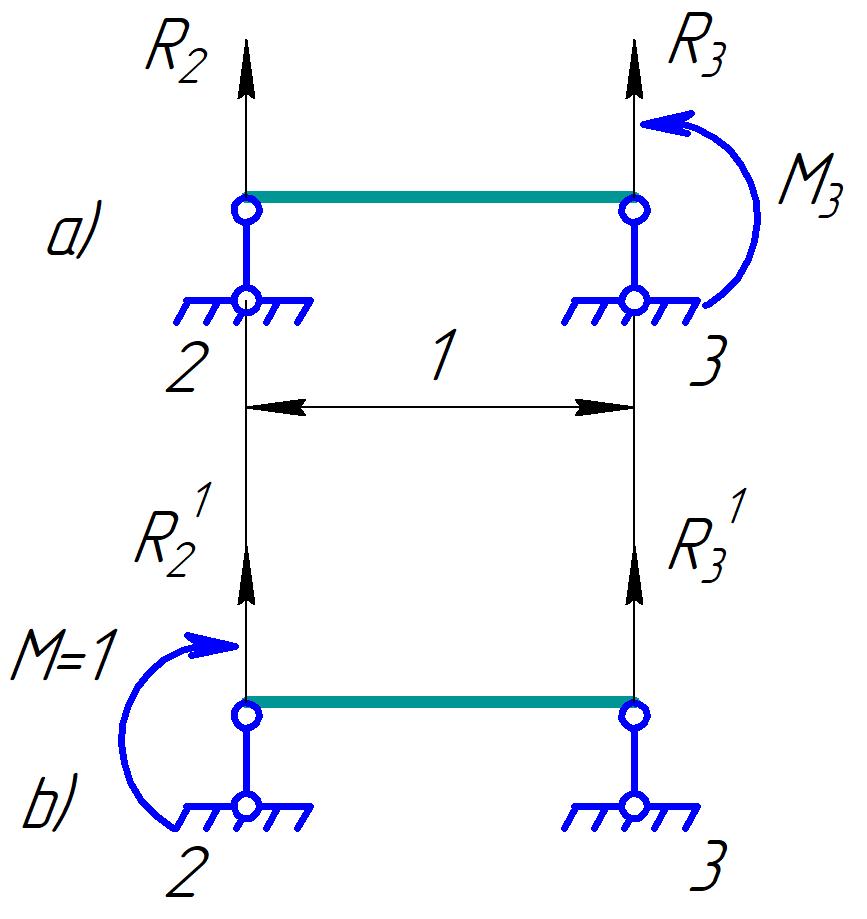 ис. 6 Рассмотрим балку, нагруженную заданной внешней нагрузкой (рис.6а). Определим реакции опор: 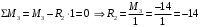 кН. кН.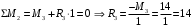 кН. кН.Составим уравнения изгибающих моментов по участкам. Начало координат на левом конце балки: 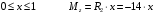 Далее снимаем внешнюю нагрузку, в сечении 2 прикладываем единичный момент (рис. 6b), составляем уравнение изгибающих моментов 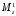 . . Реакции опор: 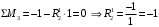 . .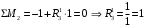 . .Уравнение моментов: 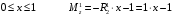 . .Составляем интеграл Мора: 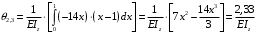 . .Подставляем полученные значения моментов и углов поворота в систему уравнений: 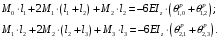 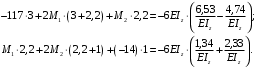 Откуда 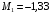 кНм; кНм; 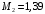 кНм. кНм.После того, как моменты 𝑀1 и 𝑀2 определены, статическая неопределимость раскрыта. Построим эпюры и очертание упругой линии балки, рассматривая каждый пролет, нагруженный внешней нагрузкой и опорными моментами, отдельно: 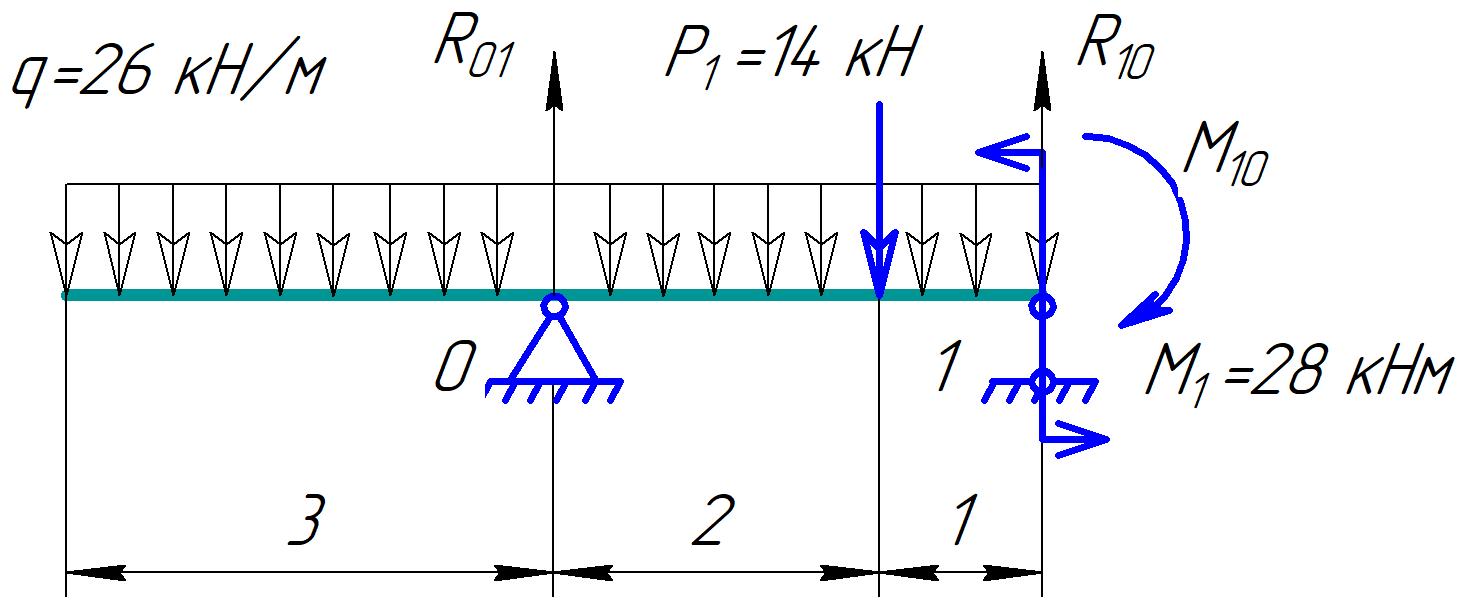 Рис. 7 Определим реакции опор: 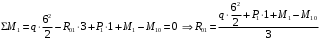 ; ;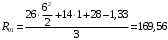 кН; кН;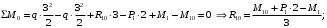 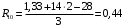 кН. кН.Уравнения сил и моментов: 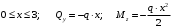 . .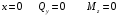 ; ;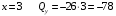 кН; кН; 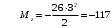 кНм. кНм.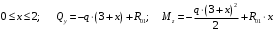 . .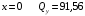 кН; кН; 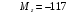 кНм. кНм.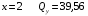 кН; кН; 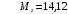 кНм. кНм.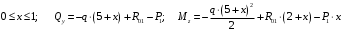 . .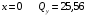 кН; кН; 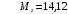 кНм. кНм.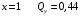 кН; кН; 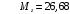 кНм. кНм.Р 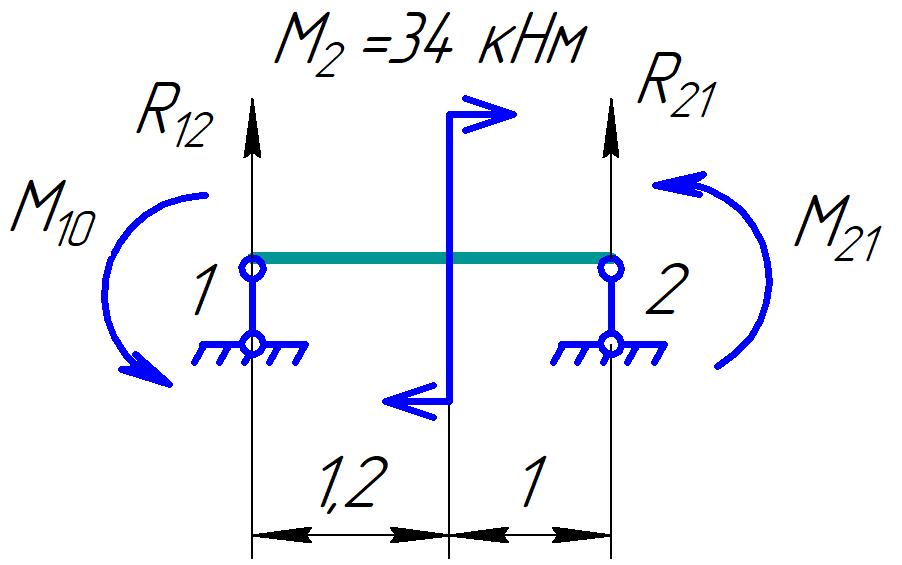 ис. 8 Определим реакции опор: 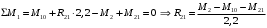 ; ;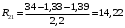 кН; кН;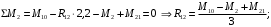 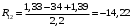 кН. кН.Уравнения сил и моментов: 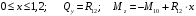 . .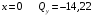 кН; кН; 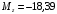 кНм. кНм.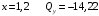 кН; кН; 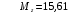 кНм. кНм.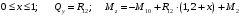 . .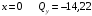 кН; кН; 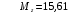 кНм. кНм.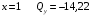 кН; кН; 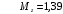 кНм. кНм.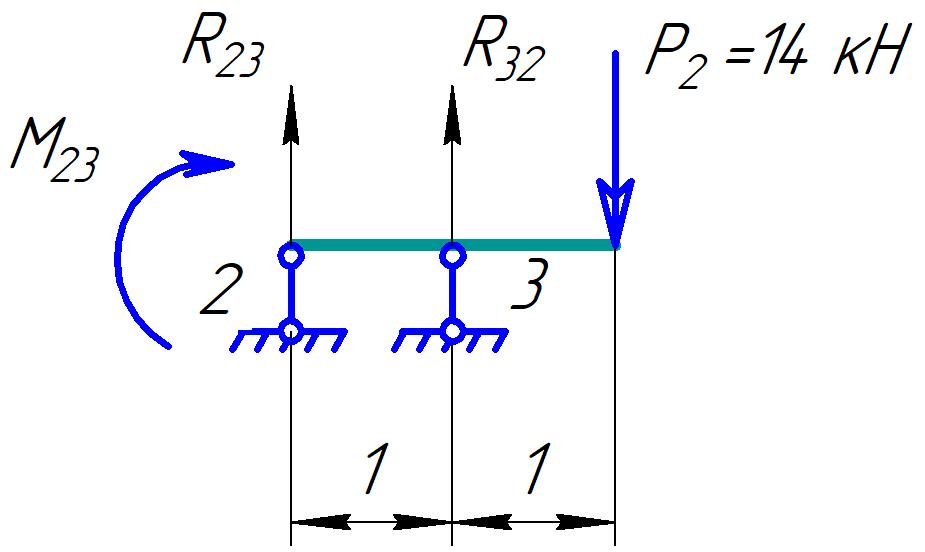 Рис. 9 Определим реакции опор: 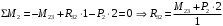 ; ;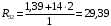 кН; кН;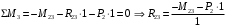 ; ;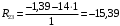 кН. кН.Уравнения сил и моментов: 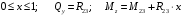 . .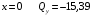 кН; кН; 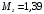 кНм. кНм.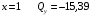 кН; кН;  кНм. кНм.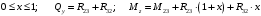 . .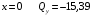 кН; кН;  кНм. кНм.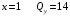 кН; кН;  . .Эпюры поперечных сил и изгибающих моментов, а также очертание упругой линии для рассматриваемой статически неопределимой балки представлены на рисунке 10. Р 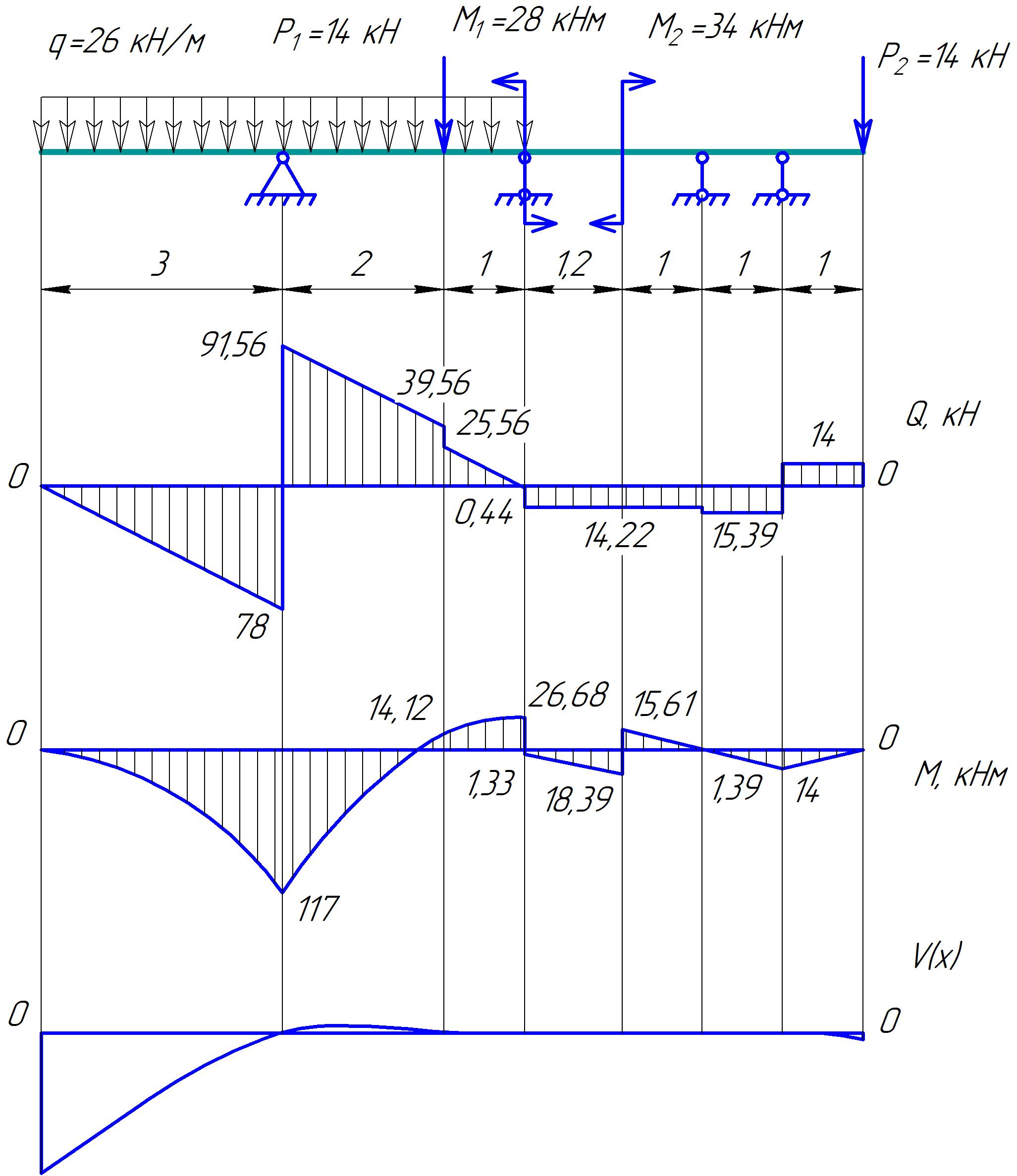 ис. 10 Из условия прочности подберем двутавровое сечение. 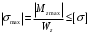 . .По эпюре моментов определяем  кНм. кНм.Подставляем это значение в условие прочности: 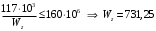 см3. см3.По сортаменту подбираем двутавр № 36 с 𝑊𝑧=143 см3. Далее необходимо убедиться в том, что условие прочности по касательным напряжениям также выполняется. Касательные напряжения вычисляем по формуле Журавского. Условие прочности по касательным напряжениям имеет вид: 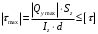 . .Из сортамента для двутавра №36 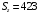 см3, см3, 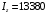 см4, см4, 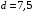 мм. мм.По эпюре поперечных сил определяем: 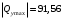 кН. кН.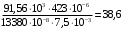 МПа МПа  МПа. МПа.Условие прочности по касательным напряжениям выполнено. |
