задачи. 5 задач. Решение Концентрация молекул газа по определению

• Название: Решение Концентрация молекул газа по определению
• Анкор: задачи
• Дата: 14.02.2022
• Размер: 87.75 Kb.
• Имя файла: 5 задач.docx
• Тип: Документы; #361074

5 задач

1.Определить концентрацию молекул кислорода, находящегося в сосуде вместимостью V=2 л. Количество вещества кислорода равно 2 моль.

Дано: V=2 л=2·10-3 м3 O2 ʋ=2 моль

n - ?

Решение:

Концентрация молекул газа по определению



Число молекул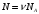



где N_A=6.02·10²³ моль^-1 – число Авогадро, тогда


Ответ: n=6,02·10²⁶ м^-3.

2.Давление воздуха внутри плотно закупоренной бутылки при температуре 7⁰ С было равно 100 кПа. При нагревании бутылки пробка вылетела. Найти, до какой температуры нагрели бутылку, если известно, что пробка вылетела при давлении воздуха в бутылке 130 кПа.

Дано: T1=70 С=280 К P1=100 кПа=105 Па P2=130 кПа=1,3‧105 Па

T2 - ?

Решение:

Т.к. бутылка закупорена, то объем газа не изменяется V=сconst, температуру при которой пробка вылетает найдем по закону Шарля:

(2)
Ответ: Т₂=364 К

3.Кинетическая энергия поступательного движения молекул азота, находящегося в в баллоне объемом 0,02 м³, равна 5 кДж, а средняя квадратичная скорость его молекул 2‧10³ м/с. Найти: 1)массу азота в баллоне; 2)давление под которым находится азот.

Дано: N2 V=0,02 м3 i=5 k> =5 кДж =5·103 Дж кв>=2‧103 м/с

m- ?

Решение:

На каждую степень свободы молекул газа приходится одинаковая средняя энергия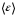

=1/2kT, где k – постоянная Больцмана; Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы соответствует две степени свободы, то средняя энергия вращательного движения двухатомной молекулы:



Кинетическая энергия движения всех молекул газа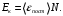



Число всех молекул газа



где N_A – постоянная Авогадро;

Тогда кинетическая энергия поступательного движения: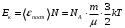



Средне квадратичная скорость молекул вычисляется по формуле: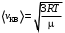

, где R=8,31 Дж/моль ·К – газовая постоянная ,T – абсолютная температура в градусах Кельвина, µ - молярная масса газа.

Отсюда выразим отношение

, но

Тогда


Ответ: m=2,5 г.
4.Два одинаковых баллона, содержащие газ при t=0⁰С, соединены узкой горизонтальной трубкой диаметром d=5 мм, посередине которой находится капелька ртути. Капелька делит весь сосуд на два объема по V=200 см³. На какое расстояние переместится капелька, если один баллон нагреть на Δ t=2⁰К, а другой на столько же охладить? Изменением объемов сосудов пренебречь.

Дано: t=00С=273 К d=5 мм=5‧10-3 м V=200 см3=2‧10-4 м3 ΔТ =2 К

х - ?

Решение:


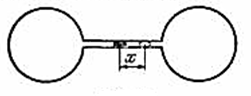Пусть p, V, T – начальные параметры газа в сосудах до изменения температуры. Изменение состояния газа при нагревании одного и охлаждении другого сосуда можно охарактеризовать следующими уравнениями: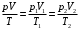



Капелька ртути станет перемещаться до тех пор, пока давление в сосудах не выровняется, т.е. р₁=р₂, что означает:



Выразим параметры объемов через смещение капельки ртути: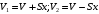



Тогда уравнение перепишется



Площадь трубки

Тогда смещение капельки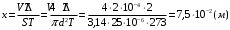




Ответ: х=7,5 см.

5.В цилиндре с площадью S=100 см² находится воздух при температуре Т=290 К. На высоте h=0,6 м от основания цилиндра расположен легкий поршень, на котором лежит гиря массой М=100 кг. Какую работу совершит газ при расширении, если его нагреть на ΔТ=50 К? Атмосферное давление р=10⁵ Па.

Дано: S=100 см2=10-2 м2 Т=290 К h=0,6 м М=100 кг ΔТ=50 К Р0=105 Па

А- ?

Решение:


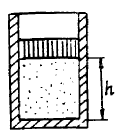Запишем уравнение Менделеева-Клайперона для газа до нагревания:

(1)

где: S – площадь поршня, h – высота поршня от дна цилиндра, m – масса газа в цилиндре, µ=29‧10^-3 кг/моль – молярная масса воздуха, R=8,31Дж/моль·К – газовая постоянная.

После нагревания это уравнение будет иметь вид:

, (2)

где Δh – величина перемещения поршня.

Вычтем из уравнения (2) уравнение (1) и выразим Δh





Работа газа при расширении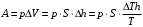



Давление газа определим из состояния равновесия до нагревания газа:



Тогда работа газа при расширении


Ответ: А=200 Дж.