контрольная. математика. Решение n 4 p 0,5 q 1 p 1 0,5 0,5

• Название: Решение n 4 p 0,5 q 1 p 1 0,5 0,5
• Анкор: контрольная
• Дата: 06.12.2022
• Размер: 136.82 Kb.
• Имя файла: математика.docx
• Тип: Решение; #830625
• страница: 1 из 2

Задание 1. Вероятность того, что баскетболист попадет в кольцо при одной попытке равна Р. Баскетболист совершил n бросков. Составить закон распределения количества попаданий. Построить многоугольник распределения. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение.

Вариант	0	1	2	3	4	5	6	7	8	9
n	3	3	2	3	4	3	2	3	3	5
Р	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,5

Решение

n = 4; p = 0,5; q = 1 – p = 1 – 0,5 = 0,5
Случайная величина X имеет область значений (0,1,2,...,n). Вероятности этих значений можно найти по формуле:

P_n(m) = C^m_np^mq^n-m

где C^m_n - число сочетаний из n по m.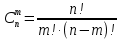



Найдем ряд распределения X.

P₄(0) = (1-p)ⁿ = (1-0.5)⁴ = 0.0625

P₄(1) = np(1-p)^n-1 = 4(1-0.5)^4-1 = 0.25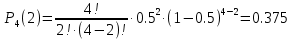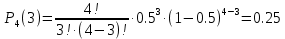





P₄(4) = pⁿ = 0.5⁴ = 0.0625

Математическое ожидание.

M[X] = np = 4x0.5 = 2

Дисперсия.

D[X] = npq = 4x0.5x(1-0.5) = 1

Проверим найденные числовые характеристики исходя из закона распределения.

xi	0	1	2	3	4
pi	0.063	0.25	0.375	0.25	0.063

Математическое ожидание находим по формуле m = ∑x_ip_i.

Математическое ожидание M[X].

M[x] = 0∙0.0625 + 1∙0.25 + 2∙0.375 + 3∙0.25 + 4∙0.0625 = 2

Дисперсию находим по формуле d = ∑x²_ip_i - M[x]².

Дисперсия D[X].

D[X] = 0²∙0.0625 + 1²∙0.25 + 2²∙0.375 + 3²∙0.25 + 4²∙0.0625 - 2² = 1

Среднее квадратическое отклонение σ(x).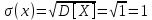



Задание 2. Из генеральной совокупности извлечена выборочная совокупность, получены значения величины. Составить безынтервальный вариационный ряд, построить полигон. Вычислить выборочное среднее значение, дисперсию, среднее квадратическое отклонение, коэффициент вариации, статистическую ошибку выборочной средней. Указать моду и медиану.

Вариант	Значения
1	67 73 69 64 69 71 59 67 69 65 63 67 71 60 69 67 71 59 67 63
2	84 82 95 83 78 98 81 82 88 87 88 89 91 95 84 82 95 95 82 82
3	75 75 72 75 66 80 75 62 70 65 73 79 72 78 78 75 66 62 65 72
4	80 75 71 76 72 82 81 78 81 73 73 73 79 75 78 76 80 73 72 81
5	98 85 94 95 92 99 96 92 95 89 101 93 98 105 100 105 101 98 92
6	67 69 64 66 67 68 67 68 69 61 60 71 71 65 61 65 71 68 68 64
7	103 90 101 97 105 91 96 86 91 93 102 93 93 101 90 97 91 96
8	45 42 45 48 42 46 49 47 48 51 42 51 53 40 46 51 46 46 48 47 51
9	130 133 135 135 137 134 130 134 135 143 135 139 135 140 130
10	102 113 96 109 97 119 102 104 102 103 100 97 102 93 92 98

Решение

Таблица для расчета показателей. Таблица для расчета показателей.

xi	Кол-во, fi	xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi	Относительная частота, fi/f
71	1	71	1	5.45	29.703	0.05
72	2	144	3	8.9	39.605	0.1
73	4	292	7	13.8	47.61	0.2
75	2	150	9	2.9	4.205	0.1
76	2	152	11	0.9	0.405	0.1
78	2	156	13	3.1	4.805	0.1
79	1	79	14	2.55	6.502	0.05
80	2	160	16	7.1	25.205	0.1
81	3	243	19	13.65	62.107	0.15
82	1	82	20	5.55	30.803	0.05
Итого	20	1529		63.9	250.95	1

П
олигон

Средняя взвешенная (выборочная средняя)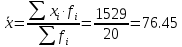



Мода.

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

Максимальное значение повторений при x = 73 (f = 4). Следовательно, мода равна 73.

Медиана.

Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим x_i, при котором накопленная частота S будет больше ∑{f/2} = 11. Это значение x_i = 78. Таким образом, медиана равна 78.

Абсолютные показатели вариации.

Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.

R = x_max - x_min = 82 - 71 = 11

Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

𝑑 = 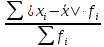= = 3.195

Каждое значение ряда отличается от другого в среднем на 3.195

Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

𝐷 = 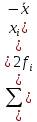= =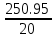 12.548

Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).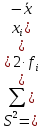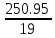

= = 13.208

Среднее квадратическое отклонение.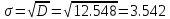



Каждое значение ряда отличается от среднего значения 76.45 в среднем на 3.542

Оценка среднеквадратического отклонения.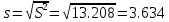



Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.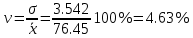



Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.

Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.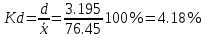



Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.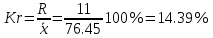


Задание 3. Составить доверительный интервал для оценки генеральной средней с доверительной вероятностью γ, если по выборке численностью n получены выборочное среднее `x и среднее квадратическое отклонение s.

Вариант	1	2	3	4	5	6	7	8	9	10
n	25	16	9	36	25	16	9	36	25	16
γ	0,95	0,95	0,95	0,95	0,99	0,99	0,99	0,99	0,999	0,999
`x	45	88	63	55	150	36	44	90	60	42
s	5	4	3	6	10	2	3	6	5	2

Решение
Найдем доверительный интервал для математического ожидания a с надежностью 0,95, используя формулу:

где γ t определяется из таблицы из условия

Ф( )= =1.96


Вывод: с вероятностью 0,95 можно утверждать, что истинное значение генерального среднего заключается в интервале [53.04; 56.96].

Задание 4. У спортсменов экспериментальной (Х) и контрольной (У) проведено тестирование. С помощью t-критерия Стьюдента определите, можно ли утверждать, что спортсмены экспериментальной группы имеют более высокий уровень подготовленности.

Вариант			Значения
1	Х	32		36	38	32	38	41	45	38
	Y	33		35	39	34	35	32	35
2	Х	74		80	76	75	70	74	72	74	70	75	70
	Y	68		70	71	70	69	72	70	73	69
3	Х	22		26	25	20	21	24	26	27	20	25
	Y	24		22	18	17	20	21	18
4	Х	85		90	92	91	90	88	88	85	84	84
	Y	80		86	82	84	85	88	81	84	80	87
5	Х	115		118	125	118	116	114	118	112
	Y	121		120	115	122	119	117	115
6	Х	5,8		5,9	5,5	5,2	5,4	5	5,3	5,3	5,1	5
	Y	5,2		5,1	4,8	5	5,1	5,2	4,9
7	Х	22		28	21	23	25	24	26	25	24	26	21
	Y	20		22	25	24	22	24	23	21	25
8	Х	52		56	58	56	54	52	58	55	55	56
	Y	48		48	50	46	52	53	54	58	58
9	Х	15,8		14,6	14,8	15,2	15,6	15,7	15,4	16	15
	Y	14,8		14,6	14,9	15,2	14,6	14,8	14,9	14	14
10	Х	38		39	35	36	38	36	36	40
	Y	39		40	42	45	45	43	42	40