задачи. Задачи (3). Решение. Найдем. Ответ 2 Таким образом. 3 Находим определитель матрицы
 Скачать 1.45 Mb.
|
|
1.1 Р е ш е н и е. Найдем 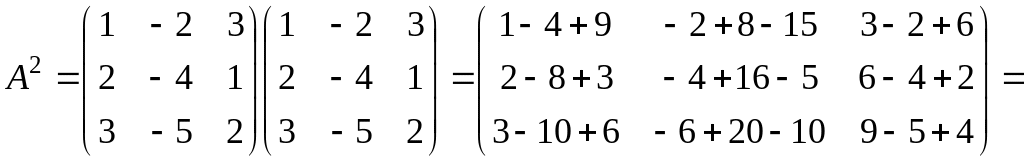 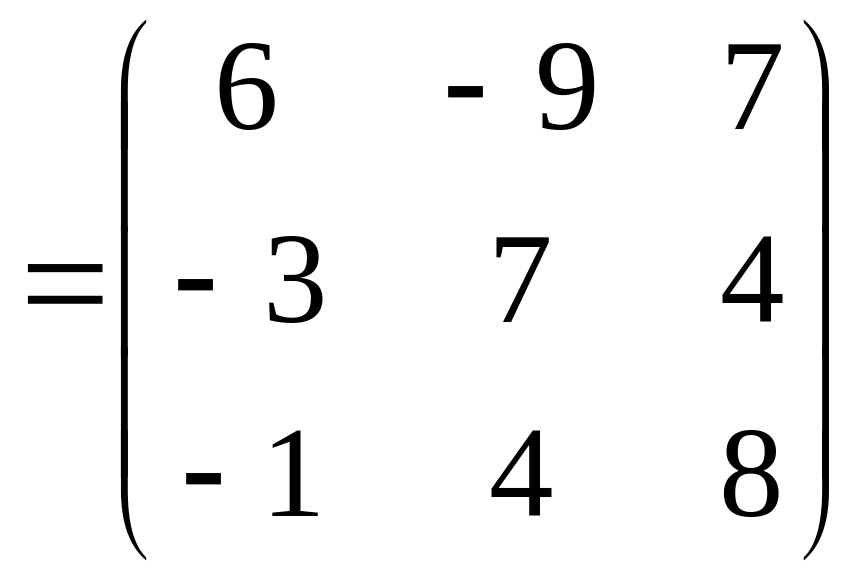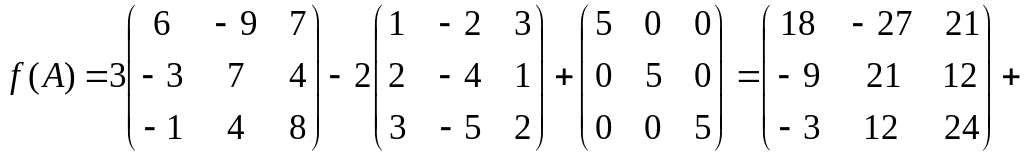.  ;  .Ответ: 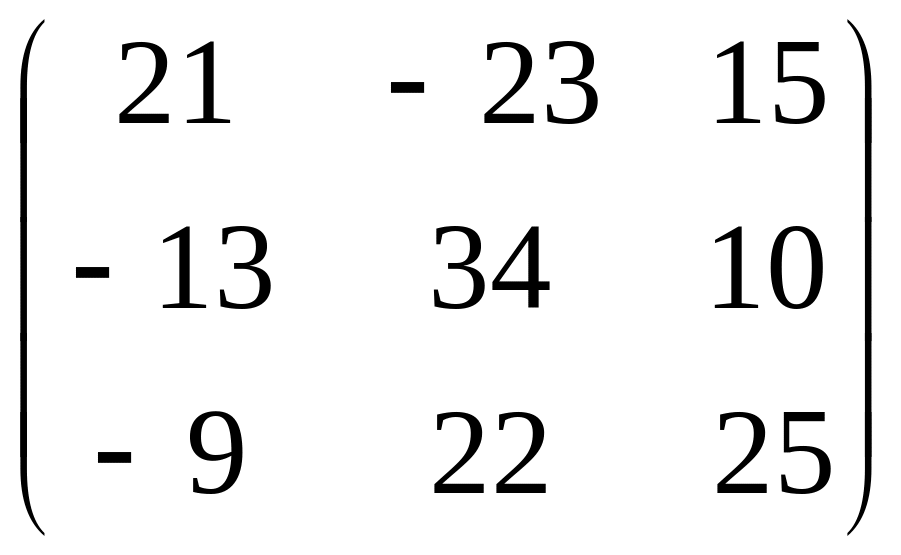 .1.2 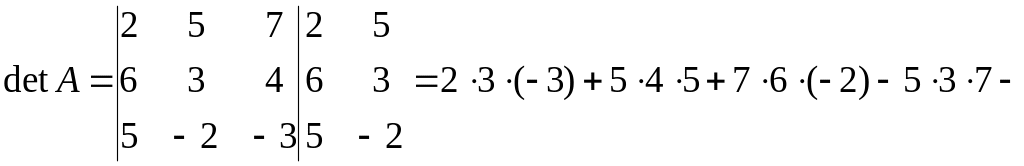  ; ;  ;  ;  ; ;  ; ;  ;  .Таким образом, 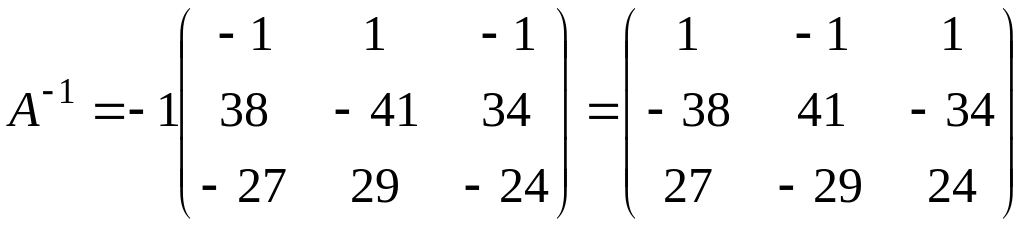 .1.3 Находим определитель матрицы 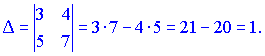 Так как детерминант не равен нулю (  ), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений Матрица дополнений примет вид  Транспонируем ее и получаем присоединенную 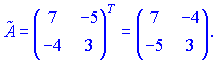  Разделим ее на определитель и получим обратную 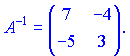 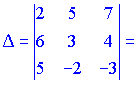   Находим матрицу алгебраических дополнений 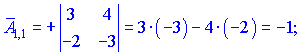 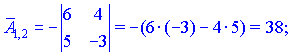 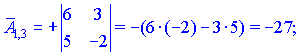 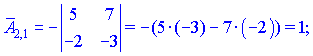 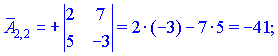 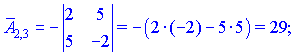 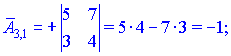 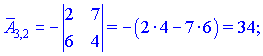 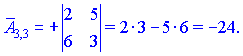  Конечный вид матрицы дополнений 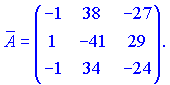 Транспонируем ее и находим союзную матрицу 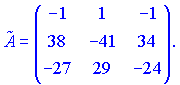 Находим обратную матрицу 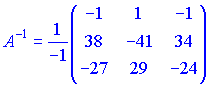 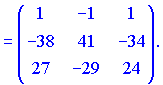 1.4 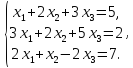 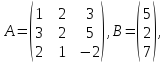 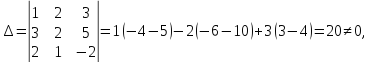 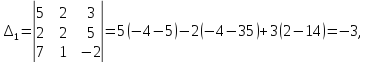 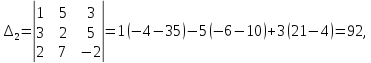 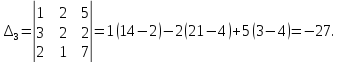 Тогда  Проверим:    1.5 z1+z2=(2–3i)+(4+3i)=2–3i+4+3i=6; z1–z2=(2–3i)–(4+3i)=2–3i–4–3i=–2–6i; z1·z2=(2–3i)·(4+3i)=2·4–3i·4+2·(3i)–(3i)·(3i)=8–12i+6i+9=17–6i ; z1:z2=2−3i4+3i=(2−3i)⋅(4−3i)(4+3i)(4−3i)= =2⋅4−3i⋅4−2⋅3i−3i⋅3i)42−(3i)2== =8−12i−6i+9)16+9=17−18i25 1.6 а)z1+z2=2-3i+1+2i=3-i б)z1+z3=2-3i-1-i=1-4i в)z1-z2=2-3i-1-2i=1-5i г)z2-z3=1+2i+1+i=2+3i д)z1×z2=(2-3i)(1+2i)=2+4i-3i-6i^2=2-6×(-1)+i=8+i е)z3×z2=(-1-i)×(1+2i)=-1-2i-i-2i^2=-1-2×(-1)-3i=1-3i 1.7
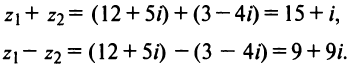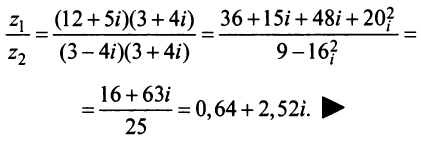    1.8 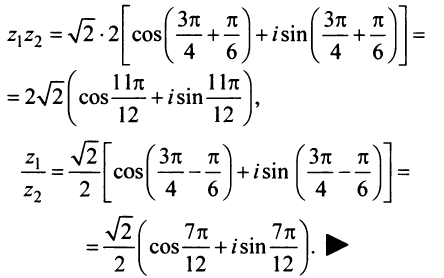 2.1 1) Найдем сторону АВ: 2 = - 3k + b -2 = 3k + b b = 0 k = (b - 2) / 3 b = 0 k = - 2/3 y = - 2/3 x Найдем сторону AC: 2 = - 3k + b -1 = 0k + b b = - 1 3k = b - 2 b = - 1 3k = - 3 b = - 1, k = - 1 y = - x - 1 Найдем сторону BC: -2 = 3k + b -1 = 0k + b b = - 1 k = (-2 - b) / 3 b = - 1 k = (-2 + 1) / 3 = - 1/3 y = - 1/3 x - 1 2) Найдем сторону AB: 6 = 2k + b 0 = - 4k + b b = 4k 6k = 6 k = 1 b = 4 y = x + 4 Найдем сторону AC: 6 = 2k + b 2 = 4k + b 2k = - 4 b = 6 - 2k k = - 2 b = 6 - 2 * (-2) = 10 y = - 2x + 10 Найдем сторону BC: 0 = - 4k + b 2 = 4k + b 2b = 2 4k = b b = 1 k = b/4 b = 1 k = 1/4 y = 1/4 x + 1 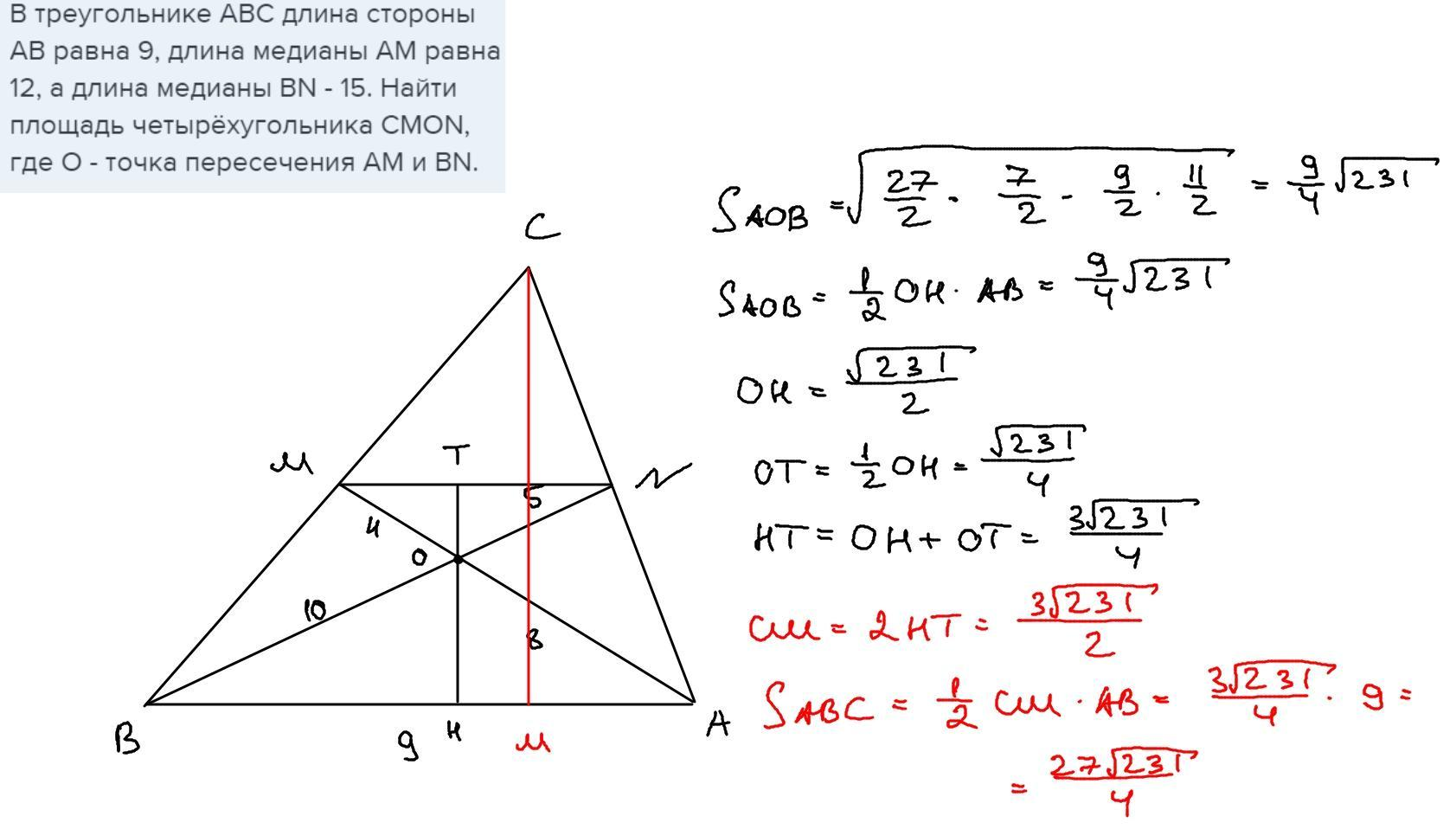 1.1  Разделим числитель и знаменатель на 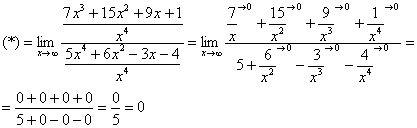  1.2  Разделим числитель и знаменатель на 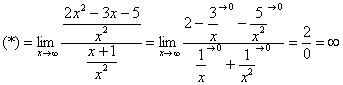  Под записью  подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.Таким образом, при раскрытии неопределенности вида  у нас может получиться конечное число, ноль или бесконечность.1.3         1.4 1) Если n=0, то функция постоянна, случай неинтересный. 2) Достаточно исследовать случай m >0, n> 0, другие случаи сводятся к этому. 3) Точки разрыва: х=0, х=n. При x --> 0 - 0 (т. е. х приближается к 0 слева) будет 2^(n/x) --> 0; f(x) --> -m/2. При x --> 0 + 0 (т. е. х приближается к 0 справа) будет 2^(n/x) --> +oo; f(x) --> 0. Значит, х=0 - точка разрыва 1-го рода (скачок) . При x --> n, 2^(n/x) --> 2; f(x) --> oo, бесконечный разрыв 1.5     1.6 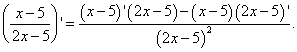 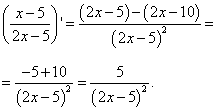 2.1 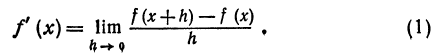 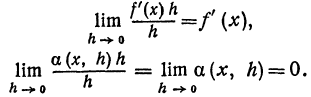    2.2  2.3 Обозначим  . Имеем ,  , ,  , ,  .Отсюда находим уравнение касательной плоскости 9(x – 2) + 14(y + 1) – 3(z – 1) = 0 или 9x + 14y – 3z–1 = 0 и уравнения нормали 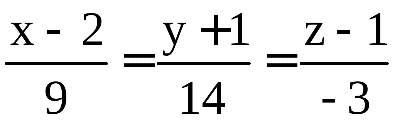 .2.4 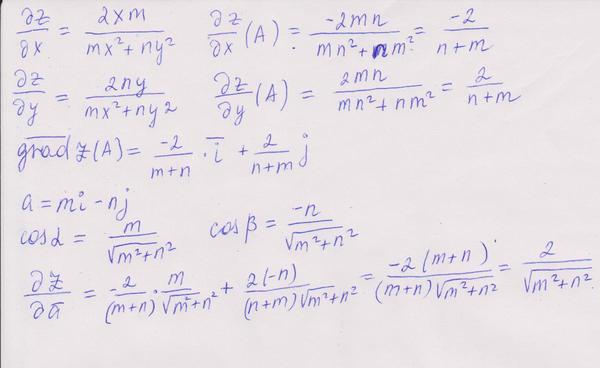 2.5 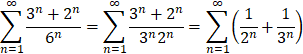 Данный ряд - сумма геометрических прогрессий со знаменателями  и    ряд сходится 2.6 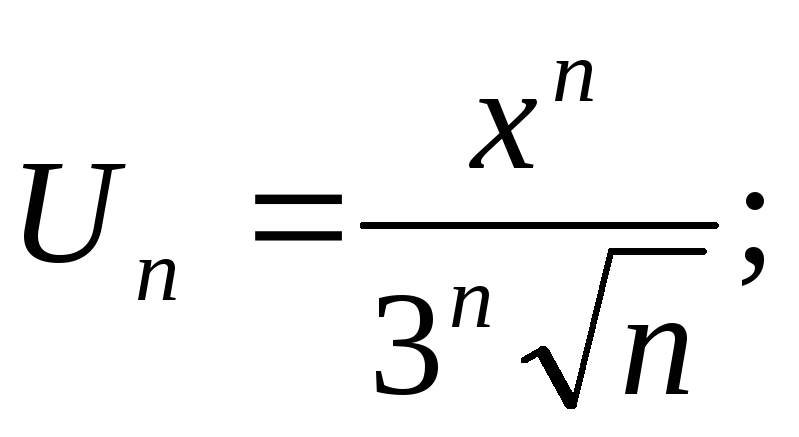 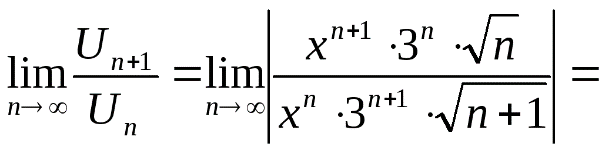 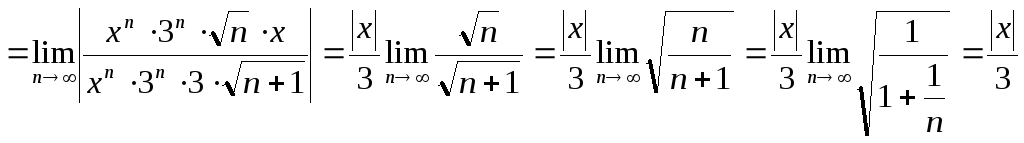 2.7 Найдем радиус сходимости R. Так как 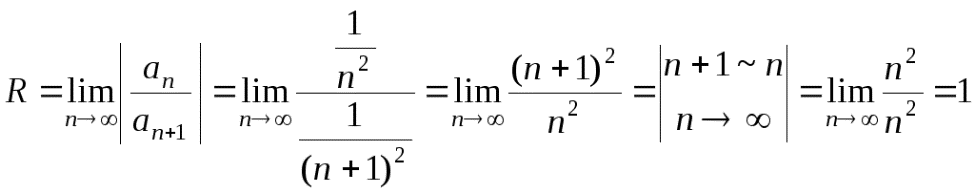 , , то .Итак, ряд сходится абсолютно для всех x, удовлетворяющих неравенству  , то есть интервал сходимости ряда .Исследуем на сходимость данный ряд на концах интервала сходимости. При  получаем числовой ряд  . Этот ряд сходится, так как является обобщенным гармоническим рядом при .При  получаем числовой ряд  . Этот ряд абсолютно сходящийся, так как ряд, составленный из абсолютных величин его членов , сходящийся.Итак, область сходимости данного ряда  .2.8  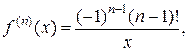         …   Подставляя эти значения в формулу, получим искомый ряд Тейлора: 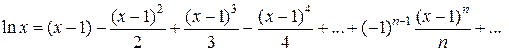 С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно,  |