Решение. Найдем потраченные кубометры и умножим их на указанную стоимость, предварительно заметив, что 13 руб. 50 коп. 13,5 руб
 Скачать 436.64 Kb. Скачать 436.64 Kb.
|
|
1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 января составляли 121 куб. м воды, а 1 февраля – 131 куб. м. Сколько нужно заплатить за холодную воду за январь, если стоимость 1 куб. м холодной воды составляет 13 руб. 50 коп.? Ответ дайте в рублях. Решение. Найдем потраченные кубометры и умножим их на указанную стоимость, предварительно заметив, что 13 руб. 50 коп. = 13,5 руб. 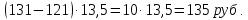 Ответ: 135. 2. На рисунке жирными точками показана цена меди на момент закрытия биржевых торгов во все рабочие дни в октябре 2010 года. По горизонтали указаны числа месяца, по вертикали – цена меди в долларах США за тонну. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену меди за данный период. Ответ дайте в долларах США за тонну. Р 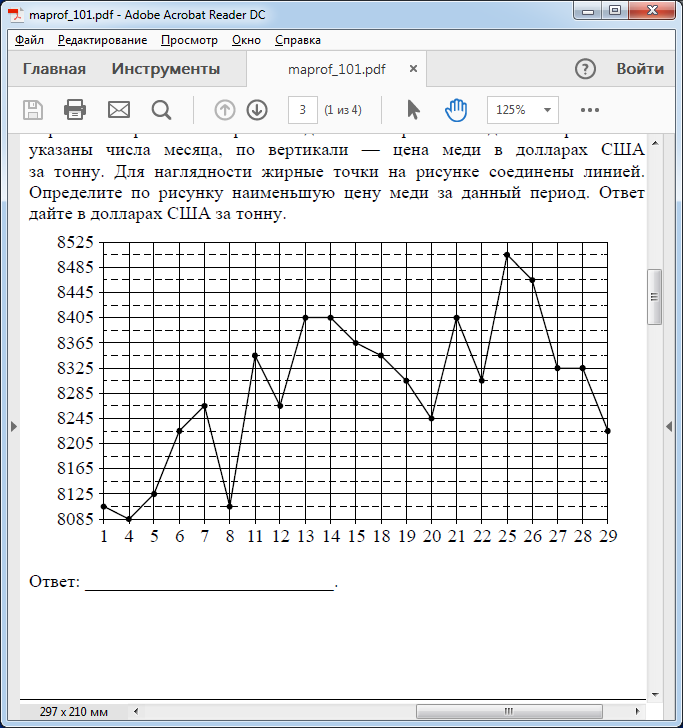 ешение. Самая нижняя точка графика соответствует отметке 8085. Ответ: 8085. 3. На клетчатой бумаге с размером клетки 1×1 изображен квадрат. Найдите радиус вписанной в него окружности. Решение. Р  адиус вписанной в квадрат окружности равен половине длины стороны квадрата. адиус вписанной в квадрат окружности равен половине длины стороны квадрата. Нетрудно посчитать по клеточкам, что длина квадрата равна 8 клеток, значит радиус равен 4. Ответ 4. 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнет игру с мячом не более одного раза. Решение. Обозначим через «1» случай, когда команда «Сапфир» начнет игру с мячом, и через «0» – противоположное событие. Тогда для команды в трёх матчах возможно 23 = 8 различных исходов: 000, 001, 010, 100, 101, 110, 011, 111. Среди восьми исходов условию задачи удовлетворяют только четыре, а именно 000, 001, 010, 100. Значит, искомая вероятность равна  Ответ: 0,5. 5. Найдите корень уравнения  . . Решение. ОДЗ:  , ,  . Переходим к равенству аргументов: . Переходим к равенству аргументов:  Ответ: –4. 6 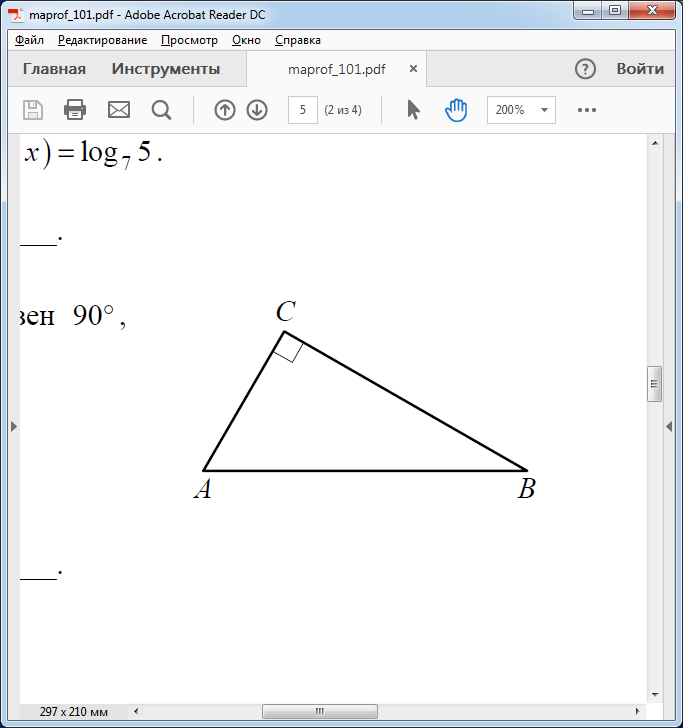 . В треугольнике АВС угол С равен 90°, . В треугольнике АВС угол С равен 90°,  , ,  . Найдите . Найдите  . . Решение. 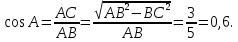 Ответ: 0,6. 7  . На рисунке изображены график функции . На рисунке изображены график функции 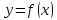 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой  . Найдите значение производной функции . Найдите значение производной функции  в точке в точке  . . Решение. Значение производной функции в точке равно тангенсу угла наклона касательной к графику функции в этой точке. Специально отмечены точки 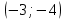 и и 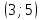 . Остается найти тангенс угла прямоугольного треугольника . Остается найти тангенс угла прямоугольного треугольника 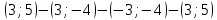 с вершиной в точке с вершиной в точке 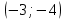 . .  Ответ: 1,5. 8  . В прямоугольном параллелепипеде . В прямоугольном параллелепипеде  известно, что известно, что  , ,  , ,  . Найдите объем многогранника, вершинами которого являются точки А, В, С, D, . Найдите объем многогранника, вершинами которого являются точки А, В, С, D, 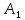 , ,  . . Решение. Указанный многогранник занимает ровно половину объема исходного параллелепипеда. Действительно, плоскость  «разрезает» «разрезает»  пополам. пополам. Поэтому  Ответ: 60. 9. Найдите значение выражения  . . Решение.  Ответ: 11. 10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы:  где t – время (в мин.),  , ,  , ,  . Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах. . Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах. Решение. Решим неравенство:   Итак, после 4 минут работы нагревательный элемент достигнет температуры 1800 К, поэтому его следует отключить. Ответ: 4. 11. Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа – со скоростью 45 км/ч, а за тем два часа – со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Решение.  Ответ: 55. 12. Найдите наименьшее значение функции  на отрезке  . . Решение. На указанном отрезке функция 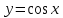 возрастает, а значит и исходная функция тоже. Поэтому её наименьшее значение найдется в начале отрезка. возрастает, а значит и исходная функция тоже. Поэтому её наименьшее значение найдется в начале отрезка.  Ответ: –35. 13. а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  Решение. 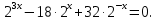 Замена 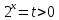 . Умножим обе части на . Умножим обе части на  : : 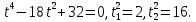 Возвращаемся к старой переменной   Отбор корней:  Ответ: а) 1/2, 2; б) 1/2. 14. Сечением прямоугольного параллелепипеда  плоскостью α, содержащей прямую плоскостью α, содержащей прямую  и параллельной прямой АС, является ромб. и параллельной прямой АС, является ромб. а) Докажите, что грань ABCD – квадрат. б) Найдите угол между плоскостями α и 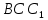 , если , если  , ,  . . Р 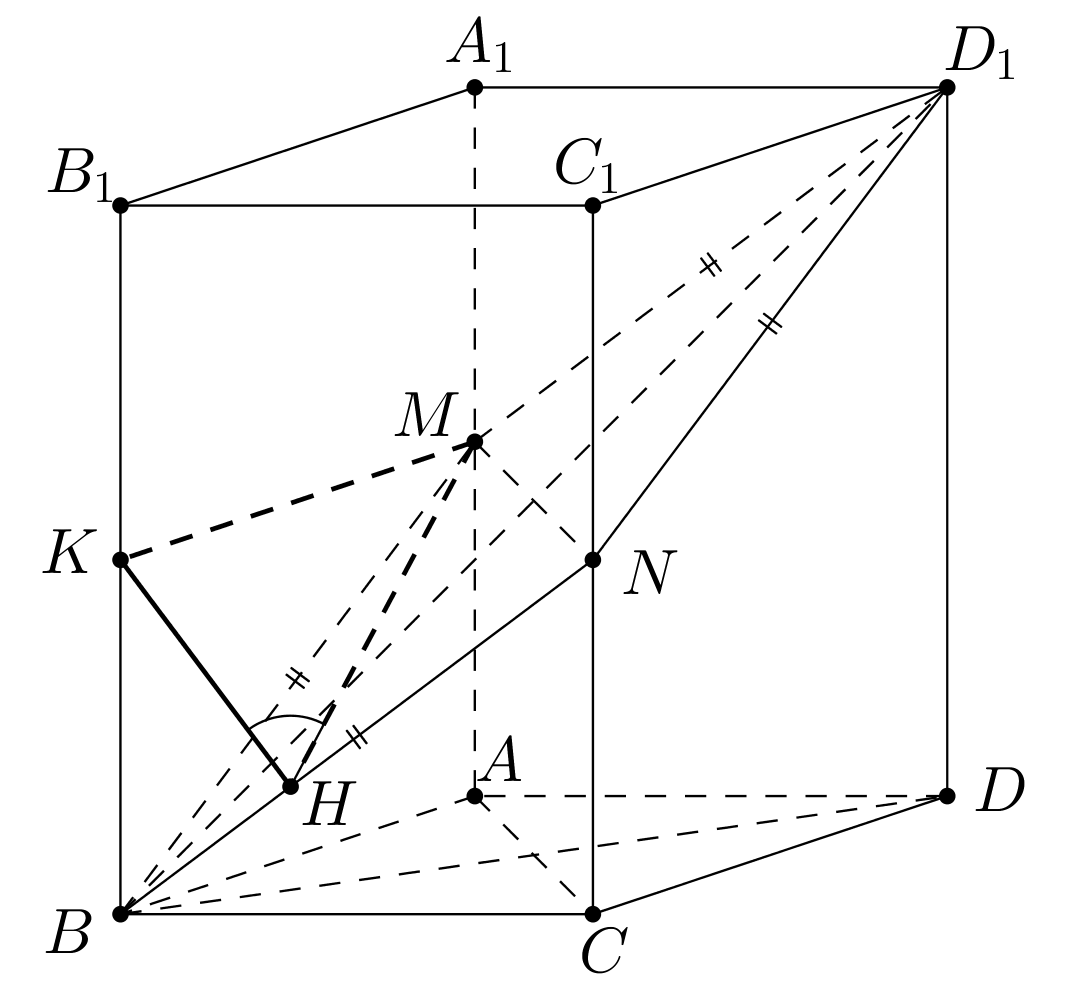 ешение. ешение.а) Диагонали ромба перпендикулярны, проекциями этих диагоналей на плоскость ABCD являются диагонали прямоугольника ABCD, которые также должны быть перпендикулярны. Значит ABCD – квадрат. б) Из доказанного следует, что треугольники BCN, BAM, 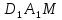 , ,  равны по катету и гипотенузе, откуда M и N являются серединами рёбер равны по катету и гипотенузе, откуда M и N являются серединами рёбер  и и  соответственно. соответственно. Проведем перпендикуляр из M к плоскости 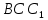 – MK. Из точки K проведем перпендикуляр к BN, получим точку Н. Угол MHK – искомый линейный угол между плоскостями. – MK. Из точки K проведем перпендикуляр к BN, получим точку Н. Угол MHK – искомый линейный угол между плоскостями. Из треугольника BKN с катетами 3 и 4 находим высоту  По построению  , поэтому угол MHK найдется: , поэтому угол MHK найдется: 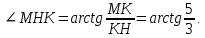 Ответ: а) ч.т.д.; б) 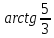 . . 15. Решите неравенство 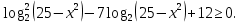 Решение. Пусть  . .  Возвращаемся к старой переменной. Исходное неравенство равносильно совокупности:  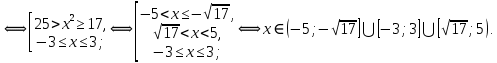 Ответ: 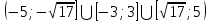 . . 16. В треугольнике ABC точки 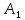 , ,  и и  – середины сторон ВС, АС и АВ соответственно, АН – высота, – середины сторон ВС, АС и АВ соответственно, АН – высота,  , ,  . . а) Докажите, что точки 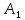 , ,  , ,  и Н лежат на одной окружности. и Н лежат на одной окружности. б) Найдите  , если , если 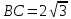 . . Решение. а)  – медиана прямоугольного треугольника АНС, поэтому – медиана прямоугольного треугольника АНС, поэтому  И  з равенства треугольников з равенства треугольников  , , 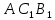 , , 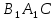 , ,  следует следует  Значит около четырехугольника  можно описать окружность. можно описать окружность. б) По теореме синусов находим:     Тогда  По теореме косинусов для треугольника  : :   Ответ: а) ч.т.д.; б) 1. 17. Пенсионный фонд владеет ценными бумагами, которые стоят  тыс. рублей в конце года тыс. рублей в конце года  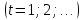 . В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в . В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 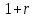 раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях  это возможно? это возможно? НЕПРАВИЛЬНОЕ РЕШЕНИЕ. Выражение для суммы на счёте: 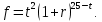 Считаем производную, ищем точку максимума: 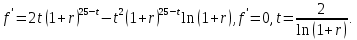 По условию, максимум достигается в конце 21 года, поэтому составим двойное неравенство:  НЕПРАВИЛЬНЫЙ ОТВЕТ:  . . ПРАВИЛЬНОЕ РЕШЕНИЕ. За год ценные бумаги увеличиваются в цене в  Видно, что относительное увеличение стоимости замедляется с каждым годом. Продавать бумаги и класть деньги в банк имеет смысл в том случае, когда в банке прирост за год (а, значит, и за все последующие годы) станет больше. По условию, продавать бумаги нужно в конце 21-го года, значит, за 21-ый год прирост стоимости ценных бумаг еще больше банковского процента, а в 22-м году – уже нет. Записываем: 21-ый год:  22-й год: 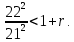  ПРАВИЛЬНЫЙ ОТВЕТ: 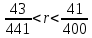 . . 18. Найдите все значения параметра а, при каждом из которых система неравенств 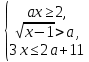 имеет хотя бы одно решение на отрезке имеет хотя бы одно решение на отрезке  . . Решение. Рассмотрим семейства следующих графиков: 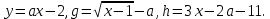 Неравенство  будет выполняться хотя бы для одного будет выполняться хотя бы для одного  из из  в том случае, если прямая в том случае, если прямая 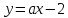 будет иметь общую точку с фигурой, ограниченной осью будет иметь общую точку с фигурой, ограниченной осью  и линиями и линиями 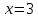 , ,  для всех для всех  . Это достигается при всех . Это достигается при всех 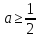 . . Из аналогичных рассуждений для 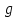 получаем получаем 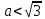 . . Неравенство  будет выполняться хотя бы для одного будет выполняться хотя бы для одного  из из  в том случае, если прямая в том случае, если прямая 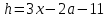 будет иметь общую точку с фигурой, ограниченной осью будет иметь общую точку с фигурой, ограниченной осью  и линиями и линиями 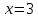 , ,  для всех для всех  . Это достигается при всех . Это достигается при всех  . . Пересекая полученные неравенства, получаем ответ. Ответ:  . . 19. На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше 40 и меньше 100. а) Может ли на доске быть 5 чисел? б) Может ли на доске быть 6 чисел? в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре? Решение. а) Да, например 6, 7, 8, 9, 10. б) Нет. Если попытаться добавить число к набору 6, 7, 8, 9, 10, которое будет меньше 6, то произведение этого числа и 6 будет меньше 40. А если к этому же набору прибавить число, большее 10, то произведение этого числа и 10 будет больше 100. в) 35. Докажем, что четыре подходящих числа 7, 8, 9, 11 обладают наибольшей суммой среди всех подходящих четверок чисел. Этот набор можно изменить, заменив 7 на 6 – сумма будет меньше. Также можно заменить 11 на 10 – снова получим уменьшение. А вот заменять число из данного набора на число, которое будет больше 11 нельзя: произведение этого числа и 10 будет больше 100. Поэтому данная четверка обладает наибольшей суммой. Ответ: а) да; б) нет; в) 35. 4ege.ru |
