Физика. Контрольная работа № 2. Решение Средняя квадратичная скорость молекул
 Скачать 108.5 Kb.
|
|
Контрольная работа № 2 203. Водород массой m = 0,30 г находится в сосуде объемом V = 2,0 л при давлении Р = 200 кПа. Найти среднюю квадратичную скорость и среднюю кинетическую энергию молекул водорода. Дано: m = 3∙10-4 кг; V = 2·10-3 м3; Р = 2·105 Па vкв – ? Еk – ? Решение Средняя квадратичная скорость молекул:  Согласно уравнению Менделеева-Клапейрона:  откуда и  Согласно основному уравнению молекулярно-кинетической теории:  откуда средняя кинетическая энергия молекул: Ответ: vкв = 2000 м/с; Еk = 600 Дж. 213. Цилиндрический сосуд, расположенный горизонтально, заполнен газом при температуре Т1 = 300 К и давлении Р1 = 0,10 МПа. Сосуд разделен на две равные части подвижной (нет трения) теплоизолированной перегородкой. Каким станет давление газа в сосуде, если в одной его половине газ нагреть до температуры Т2 = 330 К, а в другой половине температуру оставить без изменения? Дано: Т1 = 300 К; Р1 = 1·105 Па; Т2 = 330 К Р2 – ? Решение Согласно уравнению Менделеева-Клапейрона:  Т.к. изначально в каждой половине сосуда находится одинаковое количество газа, то  для той части сосуда, где нагрева не происходит; для той части сосуда, где нагрев происходит.Решая совместно эти уравнения, находим:  Ответ: Р2 = 105 кПа. 223. Кислород массой m = 10 г находится под давлением Р = 300 кПа и температуре t1 = 10ºС. После изобарного нагревания газ занял объем V2 = 10 л. Найти: изменение внутренней энергии; работу, совершенную газом при расширении; количество теплоты, полученное газом. Дано: m = 0,01 кг; Р = 3·105 Па; Т1 = 283 К; V2 = 0,01 м3 ΔU – ? А – ? Q – ? Решение Согласно закону Гей-Люссака: при Р = const V/T = const. Количество теплоты Q, поглощаемое газом при изобарном нагревании, определяется по формуле:  где  удельная теплоемкость газа при постоянном давлении. Кислород – двухатомный газ, для которого i = 5, М = 0,032 кг/моль. Таким образом:   Внутренняя энергия выражается формулой:  Ее изменение:  Работу расширения газа определим по формуле, выражающей первое начало термодинамики:  откуда:  Ответ: ΔU = 5662,71 Дж; А = 2265,09 Дж; Q = 7927,8 Дж. 233. Тепловой двигатель, работающий по циклу Карно, имеет температуру нагревателя t1 = 227ºС и холодильника t2 = 127ºС. Во сколько раз надо увеличить температуру нагревателя, чтобы к. п. д. двигателя увеличился в n = 3 раза? Дано: Т1 = 500 К; Т2 = 400 К; n = 3 Т1'/Т1 – ? Решение КПД цикла Карно:  откуда  Тогда Ответ: Т1'/Т1 = 2. 243. В вершинах квадрата помещены одинаковые заряды q = 1,0 мкКл каждый. Какой заряд нужно поместить в центр квадрата, чтобы данная система зарядов находилась в равновесии? Дано: q = 1·10-6 Кл q0 – ? Решение Согласно закону Кулона, сила взаимодействия между точечными зарядами равна:  На каждый положительный заряд, со стороны соседних двух зарядов, будут действовать силы:  где а – сторона квадрата.Со стороны диагонально противоположного заряда будет действовать сила:  Равнодействующая этих сил:  Она будет уравновешиваться силой притяжения: 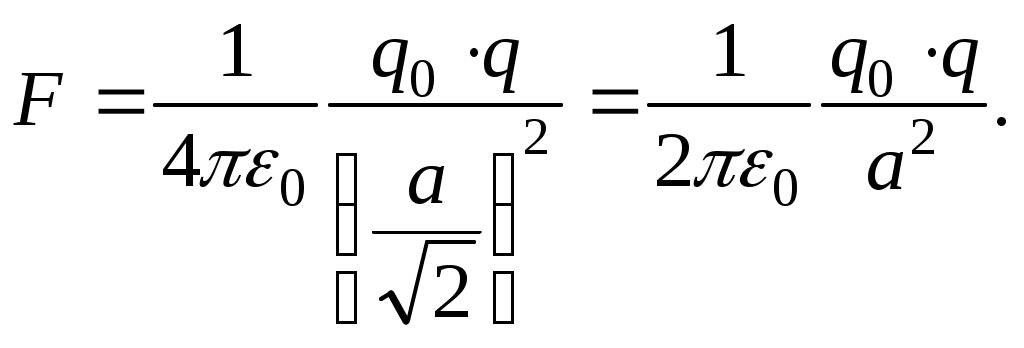 Сравнивая последние два уравнения, получаем:  Ответ: q0 = 0,957 мкКл. 253. Два электрона находятся на бесконечно большом расстоянии друг от друга. В начальный момент времени один из электронов покоился, а второй двигался по направлению к первому со скоростью v. Найти наименьшее расстояние, на которое они сблизятся. Дано: v lmin – ? Решение Под действием сил электростатического отталкивания первый электрон выйдет из состояния покоя и начнёт двигаться по той же прямой, что и второй электрон, постепенно набирая скорость. Второй электрон будет двигаться вслед за первым, постепенно теряя скорость. Расстояние между электронами будет уменьшаться до тех пор, пока скорости электронов не сравняются. обозначим скорости электронов в момент наибольшего сближения через u. Рассмотрим состояния системы 1 и 2. В общем случае импульс системы двух частиц, имеющих разные массы и движущихся первоначально с разными скоростями:  – в состоянии 1: p1 = m1υ1 + m2υ2; – в состоянии 2: p2 = (m1+ m2)u. По закону сохранения импульса: p1 = p2 → m1υ1 + m2υ2 = (m1+ m2)u. В нашем случае υ1 = 0, m1= m2 = m, υ2 = υ0. Пусть ось X направлена вдоль траектории движения электронов. Напишем закон сохранения импульса в проекциях на ось X: mυ0 = mu + mu = 2mu. В состоянии 1 полная энергия системы электронов равна кинетической энергии второго электрона, т.к. первый покоится, а потенциальная энергия взаимодействия электронов равна нулю:  В состоянии 2 полная энергия системы электронов равна сумме кинетической  и потенциальной энергий.Из закона сохранения энергии W1 = W2 имеем:  Составим систему уравнений: 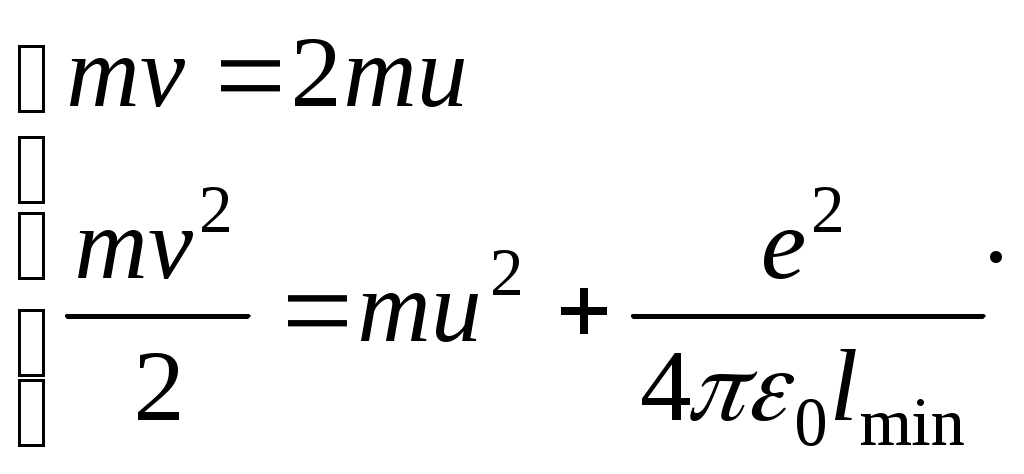 Из первого уравнения находим u = v/2 и подставляем во второе уравнение:  Ответ: |