Реферат Матка. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени
 Скачать 252.27 Kb. Скачать 252.27 Kb.
|
|
Метод распространяющихся волн В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени направлены по касательной к ее профилю. Пусть струна длины l в начальный момент направлена по отрезку оси 0x от 0 до l. Предположим, что концы струны закреплены в точках x=0 и x=l. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения - говорят, струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени. Формула Даламбера Изучение методов построения решений краевых задач для уравнений гиперболического типа мы начинаем с задачи с начальными условиями для неограниченной струны (задача Коши). utt - a2 uxx = 0, - ?<х0 (1) , t > 0 (2) 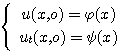 Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик: dx2 - a2 dt2 = 0 распадается на два уравнения: dx - adt = 0, dx + adt = 0 интегралами которых являются прямые x - at = c1, x + at = c2. Вводим, как обычно новые переменные: о = x + at, з = x - at. Уравнение колебаний струны преобразуем к виду: uо з = 0 (3) Найдем общий интеграл последнего уравнения. Очевидно, что для всякого решения уравнения (3) un (о, з) = f* (з) где f* (з) - некоторая функция только переменного з. Интегрируя это равенство по з при фиксированном о, получим: u (о, з) = f1 (о) + f2 (з) (4) Возвращаясь к исходным переменным (x,t), получаем: u (x,t) = f1 (x + at) + f2 (x - at) (5) данная функция является общим интегралом уравнения (1) Определим функции f1 и f2таким образом, чтобы удовлетворялись начальные условия. Для этого подставим общее решение в начальные условия (2): (6) (7) Интегрируя второе равенство, получим:  где х0 и С-постоянные.  Из полученных равенств находим: (8) 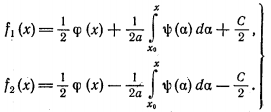 Таким образом, мы определили функции f1 и f2 через заданные функции ц и ш. Подставляя в (5) найденные значения получим: u (x,t) = f1 (x + at) + f2 (x - at) 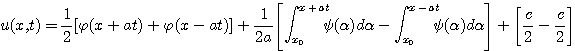 (9) Формула (9) называется формулой Даламбера. Она определяет решение задачи Коши для волнового уравнения. Неоднородное уравнение Рассмотрим задачу Коши для неоднородного уравнения колебаний tt=uxx+f (x,t), - ?<х0 t>0 -?<х1) Пусть wf (x,t,) - решение вспомогательной задачи Коши. (2) (3) Формула Даламбера (9. пункт 1) дает: (4) 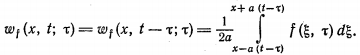 Перепишем формулу Даламбера (9. Пункт 1) в виде (5) где  являются решениями задачи (2), (3) при = 0 и f = ш (х), f = ц (х) соответственно, так как непосредственное дифференцирование показывает, что  Докажем, что справедлива следующая лемма: Решение неоднородного уравнения (1) с нулевыми начальными данными ut (x,0) - 0, u (x,0) =0 имеет вид u (х, t) = a2f (x, t; ) d (6) Дифференцируя функцию (6) и учитывая условия (3), находим (7) 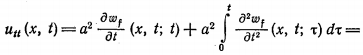 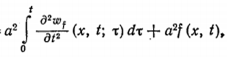 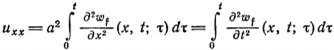 Отсюда видно, что функция (6) удовлетворяет уравнению (1). Решение задачи (1) можно представить в виде (8) 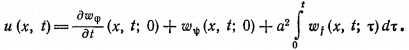 Пользуясь выражением (4), получим: (9) 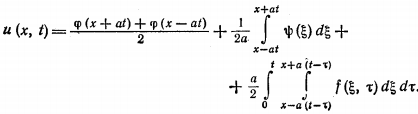 Прямая подстановка (9) в (1) показывает, что функция (9) в самом деле является решением задачи (1), если существуют производные ц'' (х), ш' (х) и df/dx. Из формулы (4) следует, что функция wf удовлетворяет уравнению при t = , если f дифференцируема по х, т.е. представление (8) возможно при тех же условиях, при которых решение задачи Коши существует. Формула (8) показывает, что решение общей задачи (1) может быть сразу написано, если имеется решение вспомогательной задачи (2) (3). Аналогичная формула имеет место и для решения задачи Коши в неограниченном пространстве.  |
