3 задачи. Решение. Средняя ошибка выборочной средней при типическом бесповторном отборе определяется следующим образом, где

• Название: Решение. Средняя ошибка выборочной средней при типическом бесповторном отборе определяется следующим образом, где
• Дата: 26.04.2022
• Размер: 42.8 Kb.
• Имя файла: 3 задачи.docx
• Тип: Решение; #496995

Вариант №4

Задание 1. Для определения средней из совокупности произведена типическая выборка. Совокупность разделена на три однородные группы численностью 3000, 5000 и 10 000 единиц соответственно. Отбор 5%-ный. Результаты, полученные по данным выборки следующие:

Группы	Выборочная средняя	Выборочная дисперсия
1	12	9
2	15	16
3	18	25

Гарантийную вероятность принять равной 0,997. Определить доверительные интервалы средней.

Решение.

Средняя ошибка выборочной средней при типическом бесповторном отборе определяется следующим образом:

, где

-средняя из групповых дисперсий выборочной средней;

n –численность выборочной совокупности по всем типическим группам (районам);

N– численность генеральной совокупности (число семей во всех

районах).

Объем выборки в каждой типической группе (районе) n_j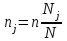



где N_j   число семей в j-м районе.

Единиц, выбранных для обследования в каждой группе при условии, что численность выборочной совокупности n по трем группам равна 900 единиц: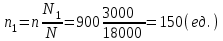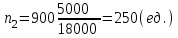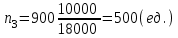



,

Среднее число по трем группам в выборочной совокупности (выборочная средняя) с учетом численности отобранных групп: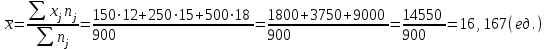



Средняя из групповых дисперсий (внутригрупповая дисперсия):

=

Средняя ошибка выборочной средней при типической выборке (средняя ошибка среднего числа в группе):

Предельная ошибка средней с вероятностью 0,997 (гарантийный коэффициент ) составит: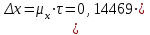

3= 0,43407 (ед.)

С вероятностью 0,997 можно утверждать, что в трех группах средняя находится в пределах: (16,167-0,43407;16,167+0,43407)=(15,73293;16,60107) или 15,73293 16,60107.

Задание 2. В сберегательных банках города методом случайной повторной выборки было отобрано 1600 счетов вкладчиков. Средний размер остатков вклада по этим счетам составил 3,2 тыс. рублей при коэффициенте вариации 30%. Какова вероятность того, что ошибка репрезентативности при определении среднего размера остатков вкладов не превысит 0,05 тыс. руб?

Решение.

Формула коэффициента вариации: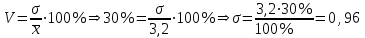

- среднее квадратическое отклонение

По условию предельная ошибка выборки

Рассчитаем среднюю ошибку выборки:

Рассчитаем значение t: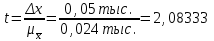



По таблице на основе значения t=2,0833 определяем вероятность того, что ошибка не превысит заданной величины. При t=2,08 вероятность Р(t)=0,95.

Задание 3.

На предприятии с числом установленных металлорежущих станков 120 единиц необходимо на основе выборочного обследования определить долю станков возрастом свыше 10 лет. Никаких предварительных данных об удельном весе этого оборудования нет. Определить, каков должен быть объем выборки с механическим отбором, чтобы при вероятности 0,954 предельная ошибка выборки не превышала 5%.

Решение.

Численность выборки можно найти по формуле:

, где

t- коэффициент доверия (при Р(t)=0,954 равен 2);

N –численность генеральной совокупности;

- предельная ошибка выборки;

- доля станков возрастом свыше 10 лет.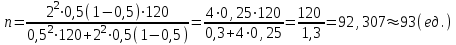