Решение Угловая скорость это первая производная от угла поворота по времени, т е. Подставим значение времени
 Скачать 431.5 Kb. Скачать 431.5 Kb.
|
|
Тема: «Механика» Вариант 2 1. Определить скорость и полное ускорение точки в момент времени 2 с, если она движется по окружности радиусом 1 м согласно уравнению φ=At+Bt3 ,где А=8м/с, В= - 1м/с2, t - криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности. Изобразить векторы скоростей и ускорений (линейных и угловых) для случая, когда окружность расположена в горизонтальной плоскости в указанный момент времени. Дано: Дано: найти: Решение Угловая скорость – это первая производная от угла поворота по времени, т.е. Подставим значение времени: Угловое ускорение – это производная от угловой скорости по времени, т.е. Подставим значение времени: Угловая скорость связана с линейной соотношением: Угловое ускорение связано с тнгенциальным( касательным ) соотношением: Нормальное и центростремительное ускорение равно 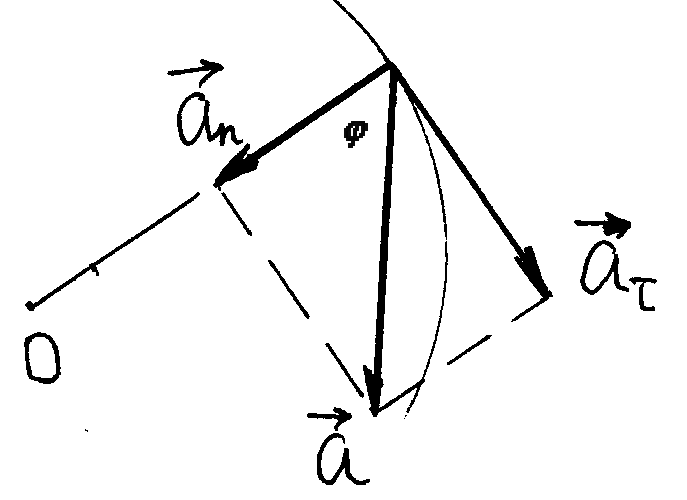 При криволинейном движении полное ускорение можно представить как векторную сумму тангенциального и нормального ускорений: Т 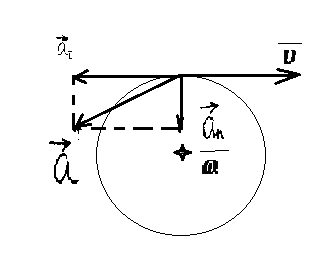 ангенциальное ускорение характеризует изменение скорости по величине и направлено по касательной к траектории в данной точке; Нормальное ускорение характеризует изменение скорости по модулю и направлено по радиусу к центру окружности . Модуль полного ускорения ангенциальное ускорение характеризует изменение скорости по величине и направлено по касательной к траектории в данной точке; Нормальное ускорение характеризует изменение скорости по модулю и направлено по радиусу к центру окружности . Модуль полного ускорения Ответ: 2. Найти работу А подъёма груза по наклонной плоскости, если масса груза m=100кг, длина наклонной плоскости l =2 м угол наклона φ=30°, коэффициент трения μ=0,1 и груз движется с ускорением a =1 м/с2. Дано: Найти: А-? Решение: 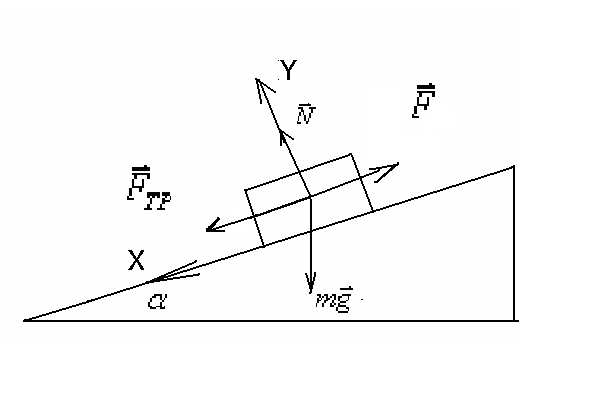 Рассмотрим силы, приложенные к телу при подъеме: Рассмотрим силы, приложенные к телу при подъеме:Найдем проекции сил на оси координат: ОХ: ОУ: Выразим силу Подставим значения: Механическая работа равна: Ответ: 3. Два шара движутся навстречу друг другу и ударяются неупруго. Скорость первого шара до удара равна 2 м/с, скорость второго 4 м/с. Пусть скорость шаров после удара равна 1м/с по направлению и совпадает с направлением скорости, которую имел первый шар до удара. Какова доля общей механической энергии шаров утеряна в процессе их соударения? Дано: Найти: Решение: При столкновении выполняется закон сохранения импульса П 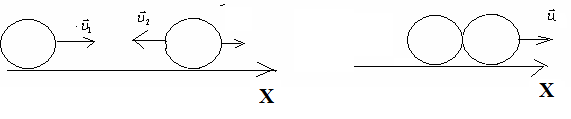 ри центральном ударе( будем считать) векторы скоростей направлены вдоль одной прямой. Поэтому в уравнении (1) можно перейти от векторов к их модулям. После неупругого удара тела двигаются как одно целое. ри центральном ударе( будем считать) векторы скоростей направлены вдоль одной прямой. Поэтому в уравнении (1) можно перейти от векторов к их модулям. После неупругого удара тела двигаются как одно целое.Тела двигались в противоположном направлении Определим отношение масс При движении тела обладали кинетическими энергиями: Энергия до столкновения была равна: После столкновения энергия стала: Так как удар неупругий , то часть энергии перешла в тепло: Ответ 4. Уравнение колебаний материальной точки массой 5 г, имеет вид Х=0,02cos5t, где все величины измеряется в соответствующих единицах СИ. Определить максимальное значение силы, действующей на точку, и максимальное значение кинетической энергии точки. Дано: Найти: Решение: запишем уравнение гармонических колебаний в общем виде Максимальная кинетическая энергия тела, совершающего колебания равна : Скорость- первая производная от пути по времени, т.е. Амплитудное значение скорости равно Подставим выражение(3) в (2) Согласно 2 закону Ньютона : Ускорение - первая производная от скорости по времени, т.е. Амплитудное значение ускорения равно Подставим (5) в (4) Подставим значения. Ответ: 5. Основы релятивистской механики. Преобразования Лоренца. Взаимосвязь энергии и массы. Релятивистская механика изучает движение частиц, у которых скорость близка к скорости света в вакууме. Она основана на специальной теории относительности Эйнштейна. В основе лежат два постулата: 1. ( принцип относительности). Никакие опыты, проведенные внутри с данной инерциальной системы, не дают возможности обнаружить покоится эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной сиситемы. 1 постулат является обобщением механического принципа относительности Галилея: любые физичечские законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы одинаковы по форме во всех инерциальных системах отсчета. 2.( принцип инвариантности скорости света). Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Из постулатов Эйнштейна следует, что скорость света в вакууме- максимально возможная скорость. Преобразования, в основе которых лежат постулаты Эйнштейна, называются преобразованиями Лоренца. С учетом того, что все инерциальные системы отсчета равноправны, преобразования Лоренца должны быть линейными относительно системы К(x,y,z,t ) и системы Пусть одна система покоится, а вторая движется вдоль оси абсцисс. Здесь как видим, время также изменяется наряду с координатами, то есть выступает как бы в роли четвертной координаты. Преобразования Лоренца показывают, что в СТО пространство и время неразделимы в отличие от классической механики. Пусть сиситема К(x,y,z,t ) покоится , а 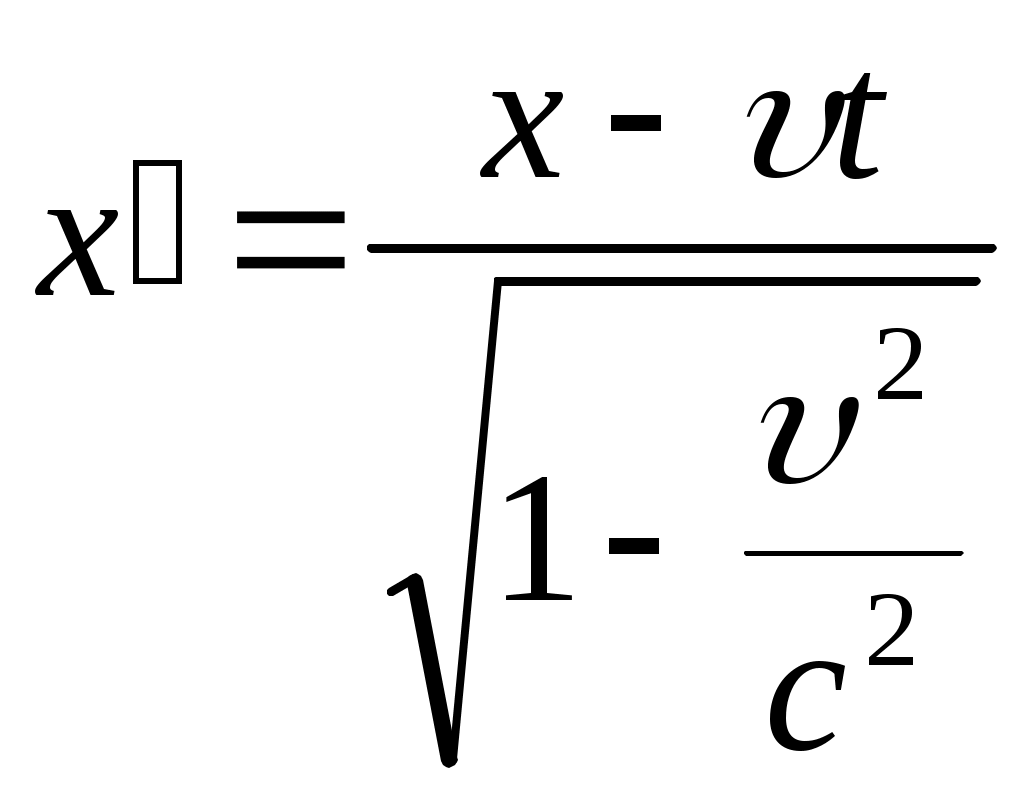 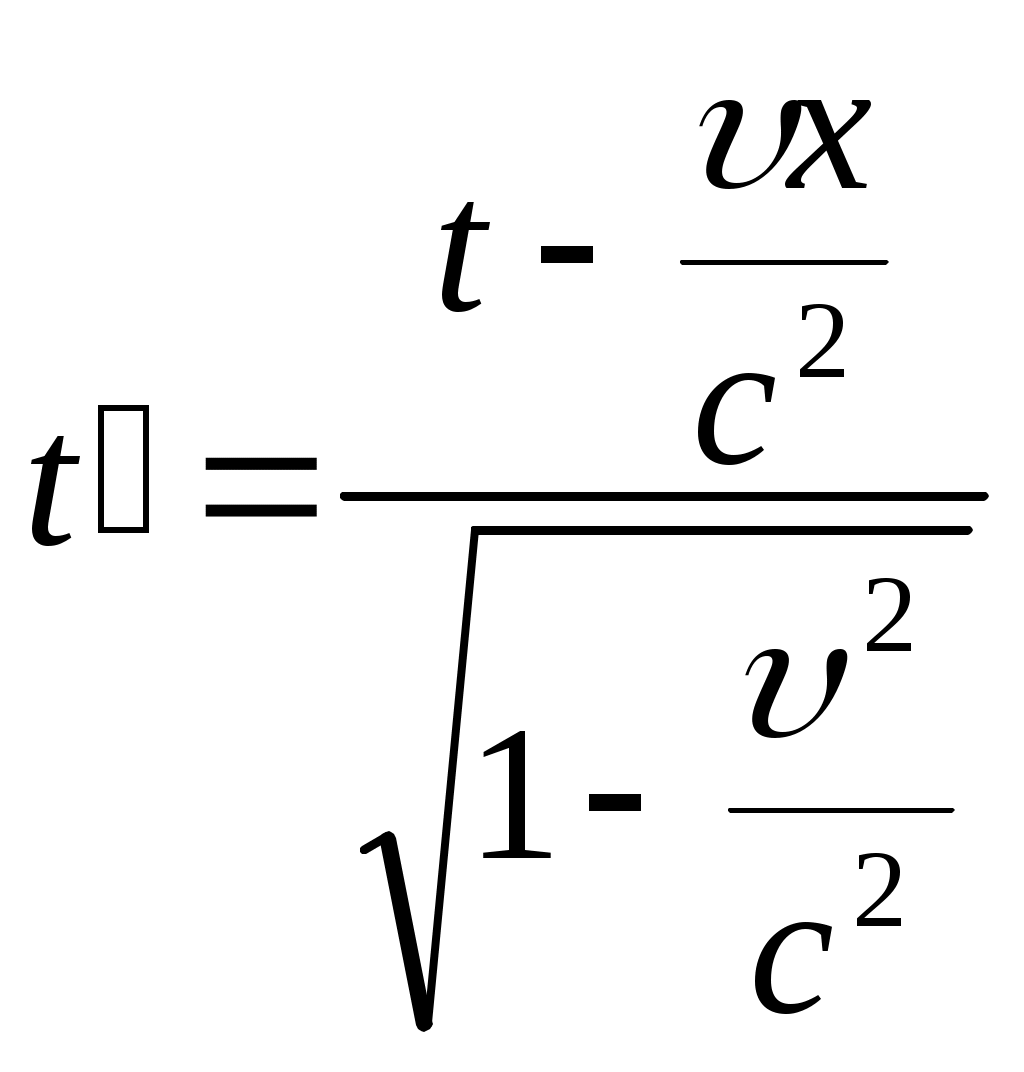 При скоростях Следствие изпреобразования Лоренца . относительность одновременности 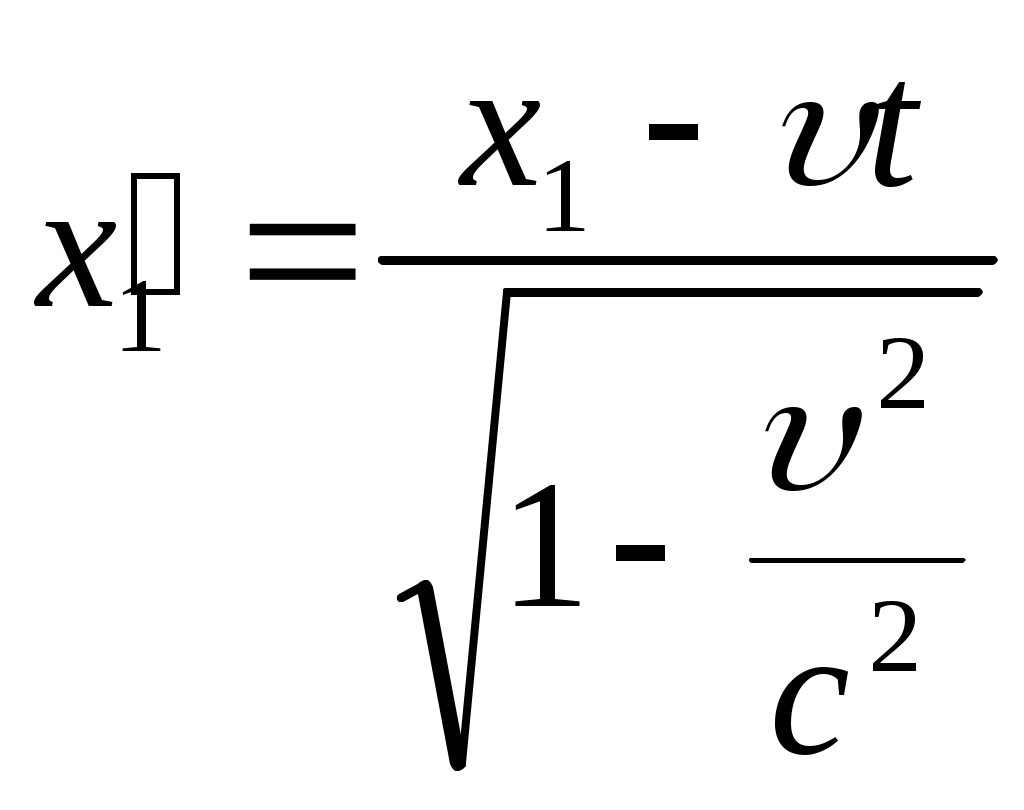 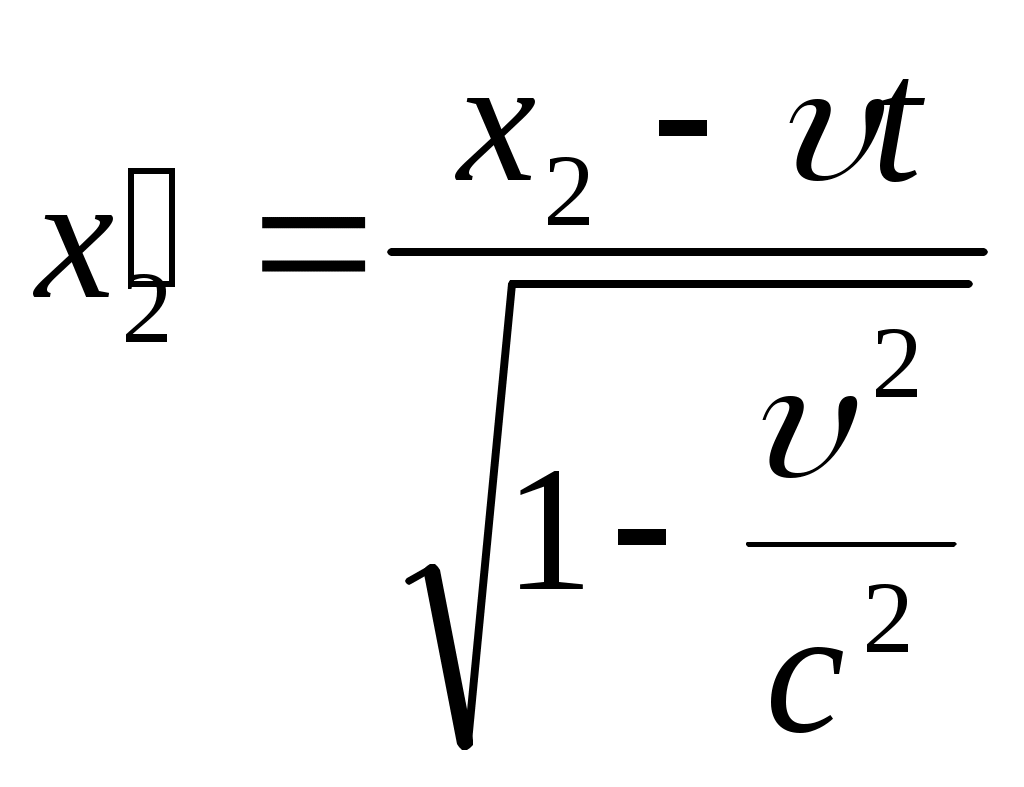 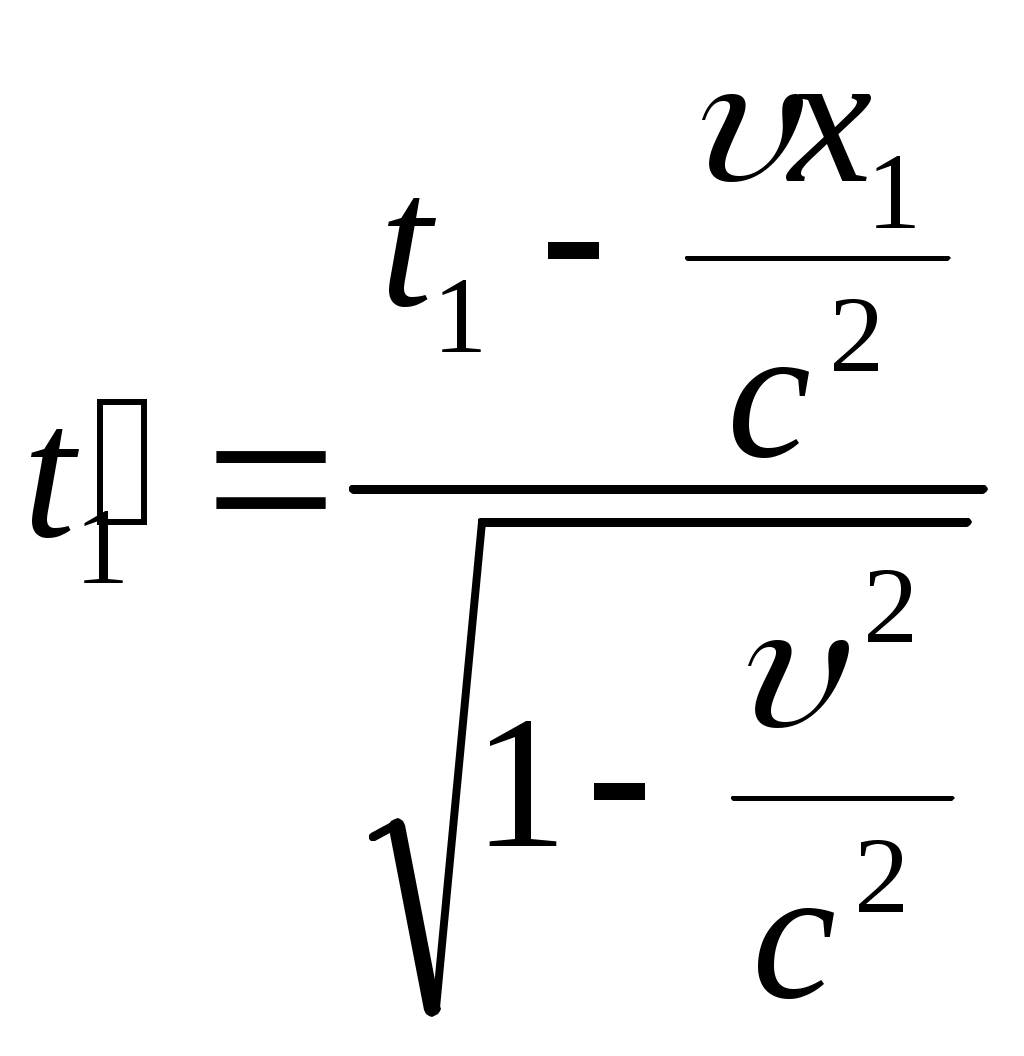 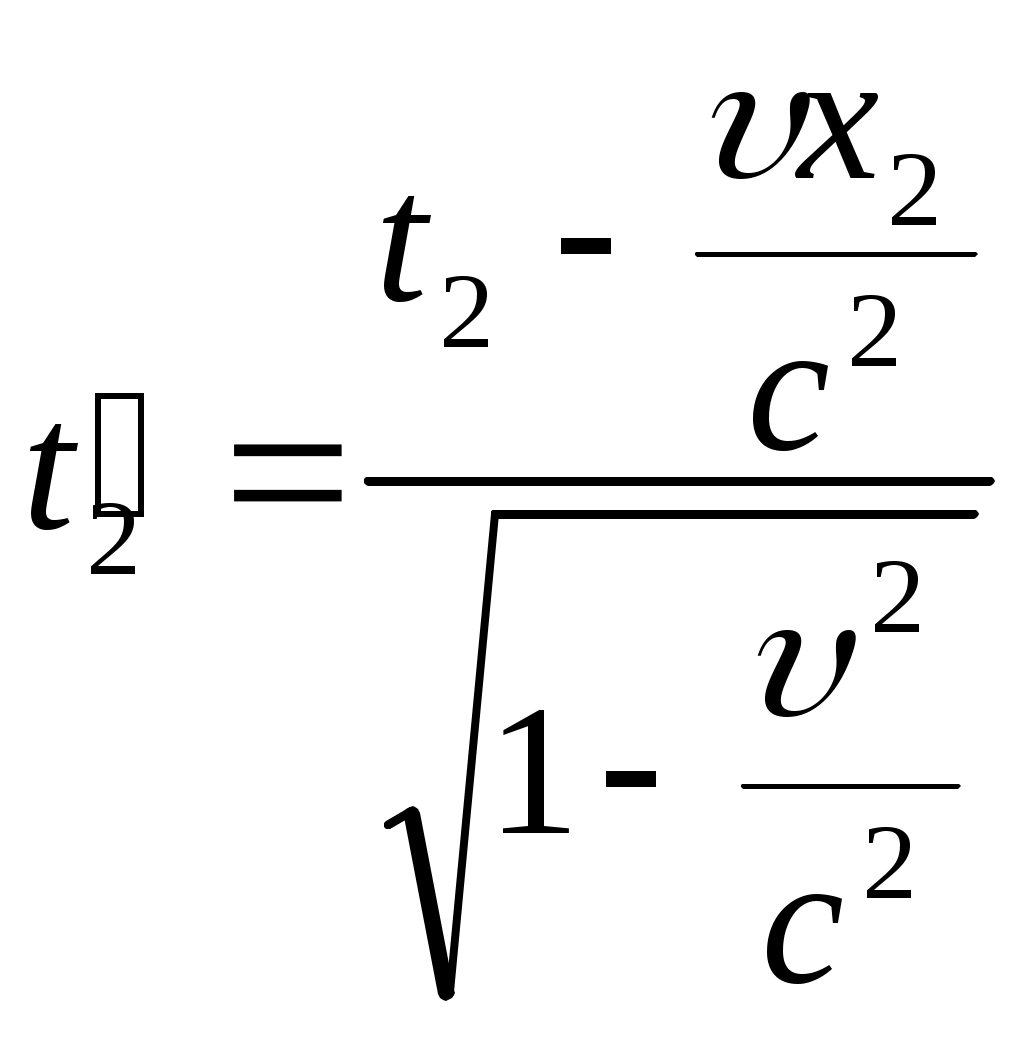 , , события в системе К разобщены, но одновременны, а в системе длительность событий в разных системах отсчета 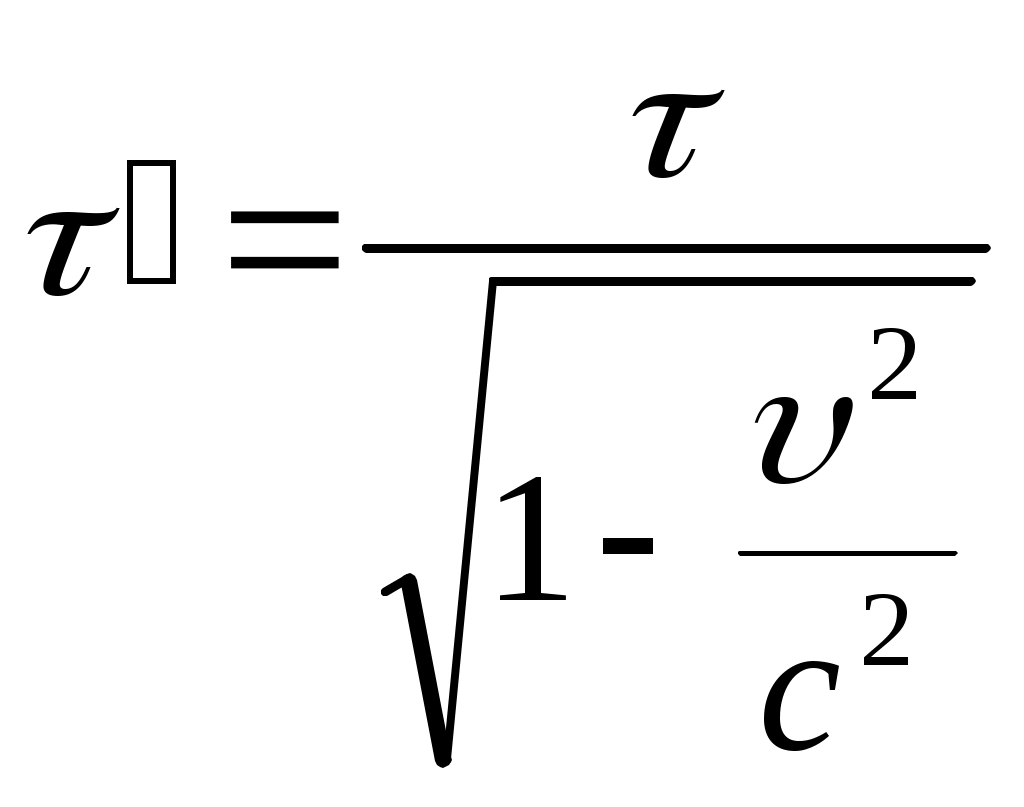 ( длительность события меньше в той инерциальной системе, относительно которой тело покоится) ( длительность события меньше в той инерциальной системе, относительно которой тело покоится)Длина тел в разных системах отсчета 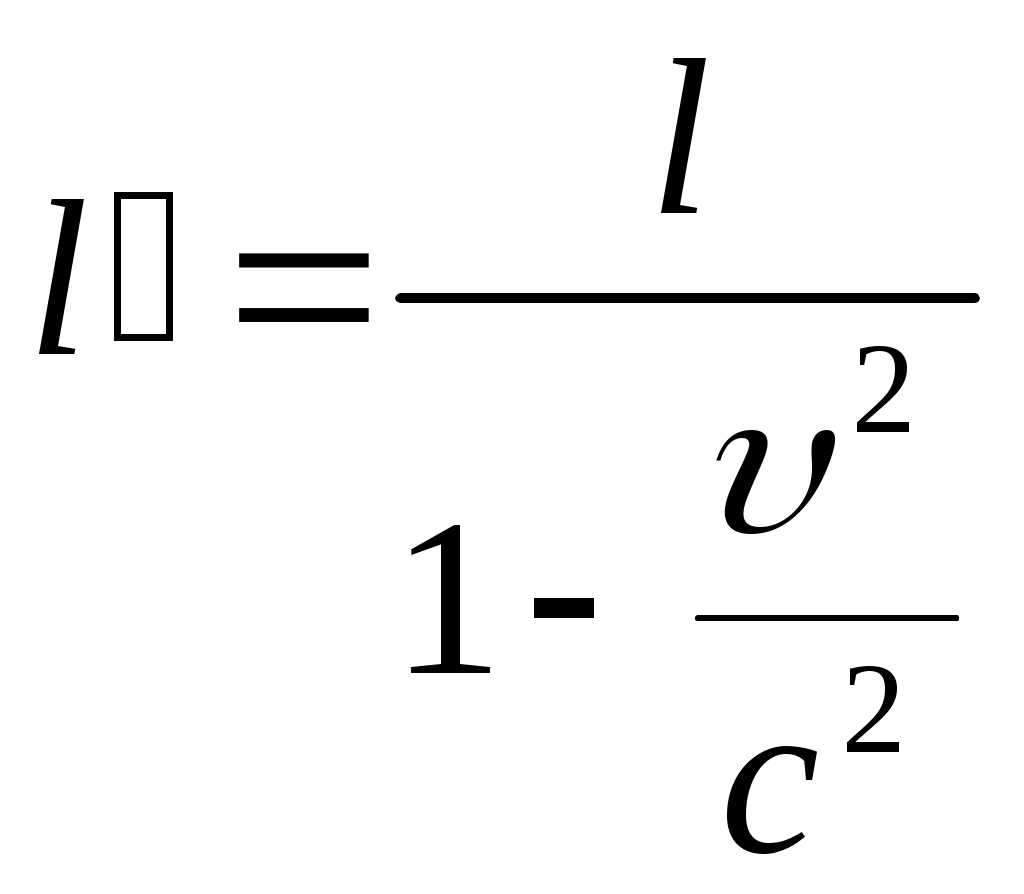 ( линейные размеры больше в той инерциальной системе, относительно которой тело покоится) ( линейные размеры больше в той инерциальной системе, относительно которой тело покоится)Закон соотношения между массой и полной энергией можно выразить следующей формулой: 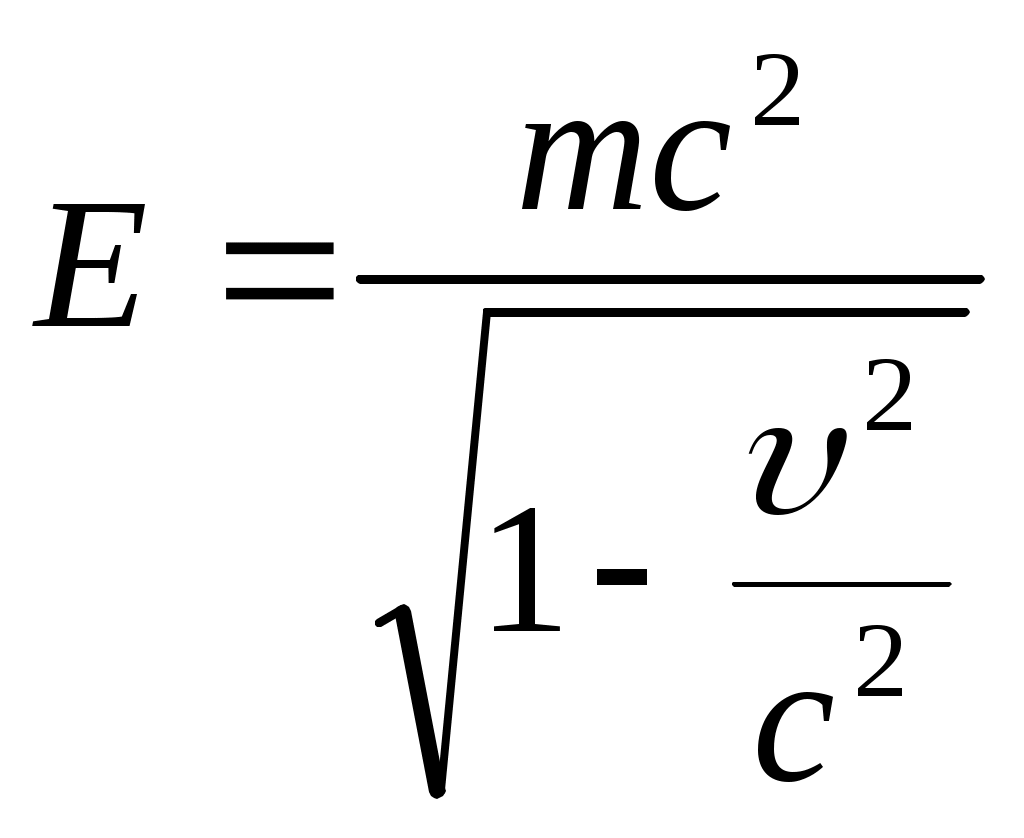 Тело обладает энергией и при нулевой скорости. Такая энергия называется энергией покоя. 6. Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны в 100 м. На какой угол при этом он должен накрениться, чтобы не упасть при повороте? 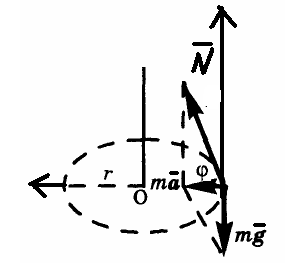 Дано: Найти: Решение: Укажем силы действующие на мотоциклиста. Запишем второй закон Ньютона: ОХ: ОУ: Разделим уравнение (2) на (1): 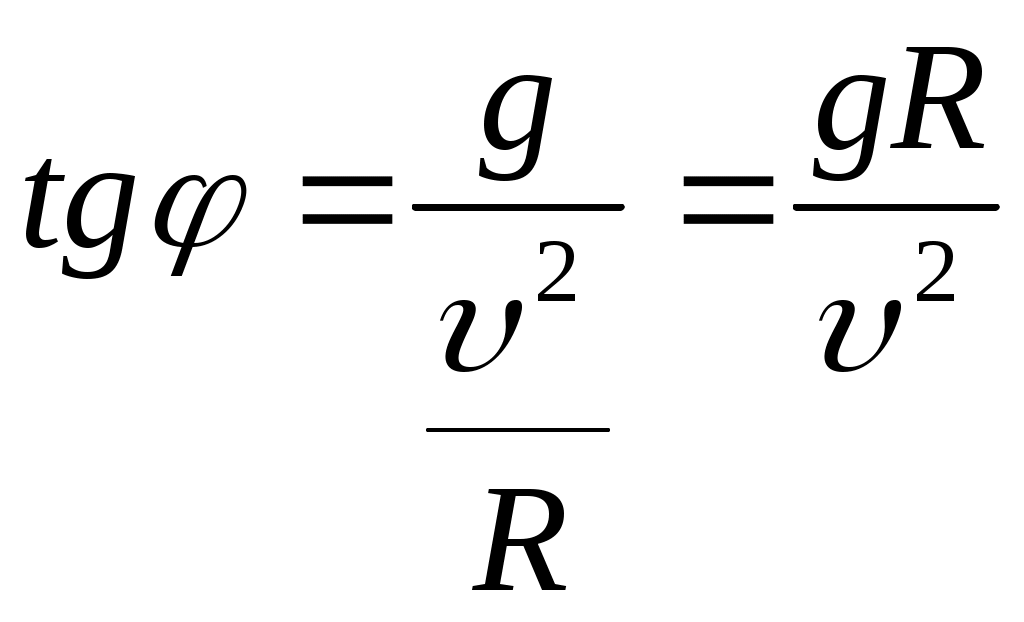 Ответ. 7. Найти линейную скорость и нормальное ускорения движения Луны по орбите вокруг Земли. Орбиту считать круговой. Дано: Найти : Решение: На спутник действует сила всемирного тяготения Уравниваем правые части выражений (1) и (2) Нормальное ускорение равно Ответ: 8. На барабан массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг. Груз находится на высоте 2 м над уровнем пола. За какое время груз достигнет пола и чему будет равен вес груза во время движения? Дано: Найти: Решение: Укажем силы действующие на груз. Запишем 2 закон Ньютона для груза: Найдем проекции сил на ось ОУ: 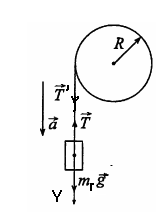 Барабан приводится во вращение силой натяжения нити Барабан приводится во вращение силой натяжения нити 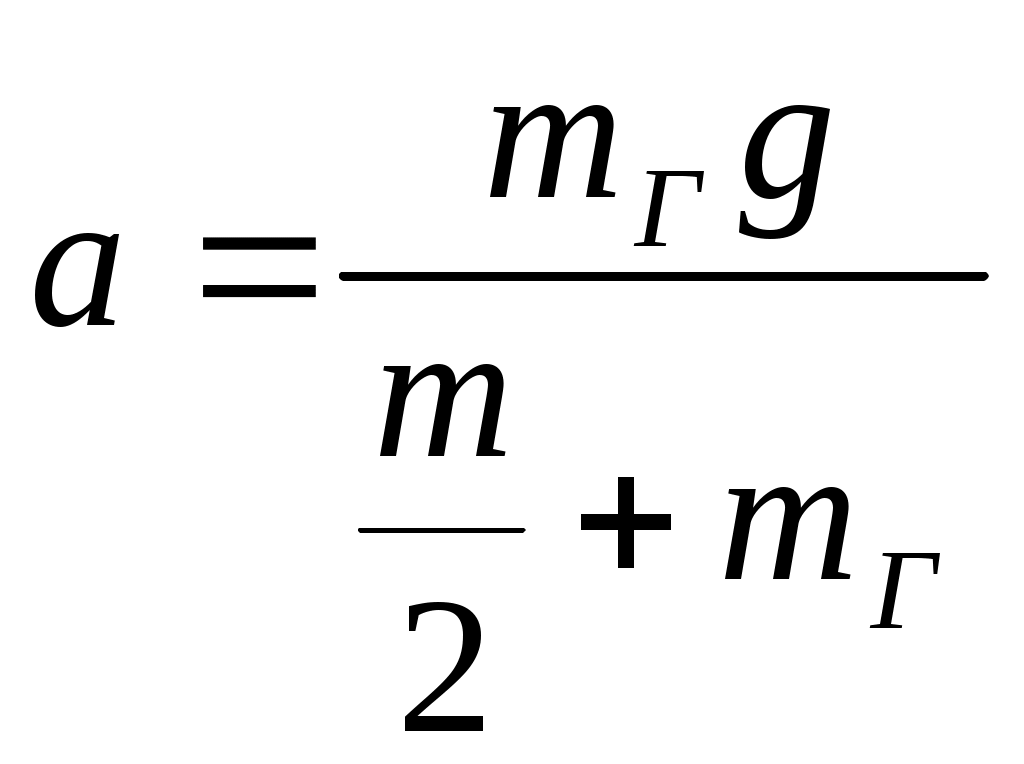 . Подставляем значения . Подставляем значения 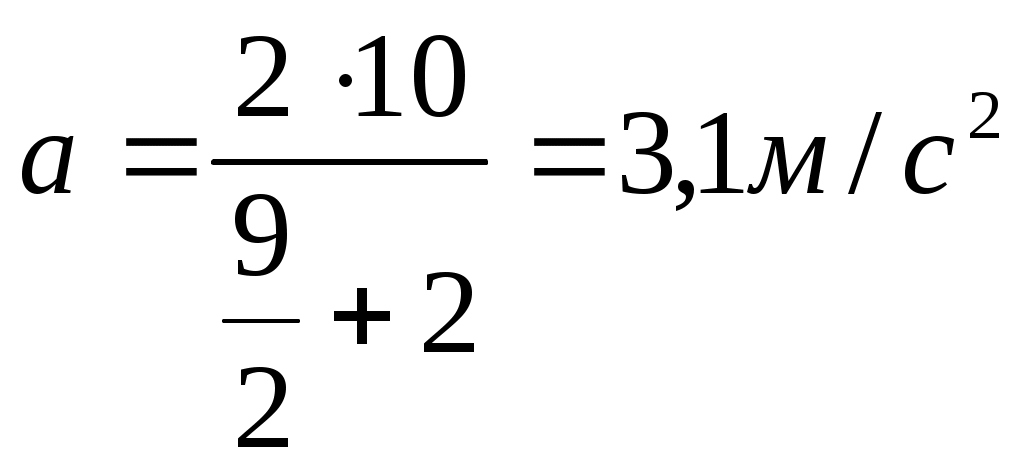 Определим время спуска: В проекциях на ось ОУ: Поо 3 закону Ньютона Ответ: 9. На краю платформы в виде диска, вращающегося по инерции вокруг вертикальной оси с частотой 8 мин-1, стоит человек массой 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой 10 мин-1. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки. Дано: п  латформа- диск , латформа- диск , Найти : Решение: Для тел имеющих ось вращения , выполняется закон сохранения момента импульса Момент импульса по определению равен : Подставим значения Ответ: |
