Решение в силу условия для тонкого клина (см рисунок) где y толщина клина в том месте, где наблюдается темная полоса
 Скачать 44.65 Kb. Скачать 44.65 Kb.
|
|
505. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны 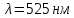 . Расстояние между соседними темными интерференционными полосами в отраженном свете . Расстояние между соседними темными интерференционными полосами в отраженном свете  . Определить угол α между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, . Определить угол α между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин,  . .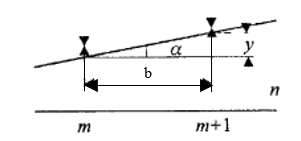 Решение: 1. В силу условия для тонкого клина (см. рисунок) 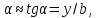 где y – толщина клина в том месте, где наблюдается темная полоса. 2. Разность хода двух волн для условия интерференционных минимумов 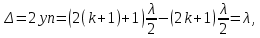 (k = 0, 1, 2, …), (k = 0, 1, 2, …),следовательно 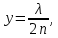 откуда 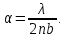 Подставляя исходные данные, получим 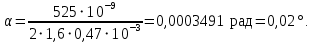 Ответ: 0,02◦. 515. На грань кристалла падает параллельный пучок рентгеновского излучения ( 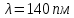 ). Под углом ). Под углом  к поверхности кристалла наблюдается дифракционный максимум второго порядка. Определить расстояние d между атомными плоскостями кристалла. к поверхности кристалла наблюдается дифракционный максимум второго порядка. Определить расстояние d между атомными плоскостями кристалла.Решение: Запишем формулу Брэгга-Вульфа: 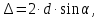 где 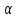 – угол скольжения. Для нашего случая разность хода: – угол скольжения. Для нашего случая разность хода: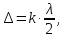 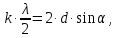 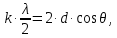 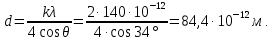 Ответ: 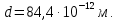 525. Угол между плоскостями пропускания поляроидов равен 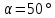 . Естественный свет, проходя через такую систему, ослабляется в n=4 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах. . Естественный свет, проходя через такую систему, ослабляется в n=4 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах.Решение:  При прохождении через первый николь (если свет ествественный) получаем: 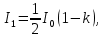 После второго николя: 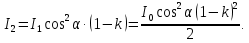 Тогда:  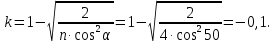 535. На поверхность калия падает свет с длиной волны 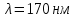 . Определить максимальную кинетическую энергию . Определить максимальную кинетическую энергию 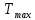 фотоэлектронов. фотоэлектронов.Решение: Формула Эйнштейна для фотоэффекта: 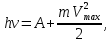 где 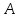 – работа выхода. – работа выхода.Найдем максимальную кинетическую энергию фотоэлектронов, вырываемых из этого металла светом с длиной волны 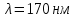 . Частота этой длины волны равна: . Частота этой длины волны равна: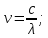 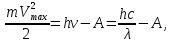 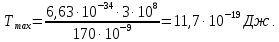 545. Фотон с энергией 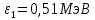 был рассеян при эффекте Комптона на свободном электроне на угол был рассеян при эффекте Комптона на свободном электроне на угол 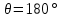 . Определить кинетическую энергию . Определить кинетическую энергию 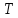 электрона отдачи. электрона отдачи.Решение: Запишем уравнение Комптон – эффекта: 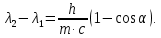 Отсюда длина волны рассеянного излучения равна:  Поскольку 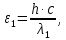 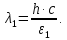 Тогда: 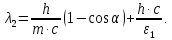 Запишем закон сохранения энергии, откуда и выразим кинетическую энергию электрона: 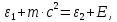 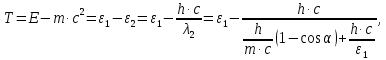 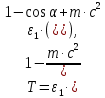 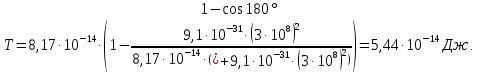 555. Давление света с длиной волны  , падающего нормально на черную поверхность, равно , падающего нормально на черную поверхность, равно  . Определить число N фотонов, падающих за время . Определить число N фотонов, падающих за время 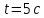 на площадь на площадь 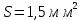 этой поверхности. этой поверхности.Решение: Давление света: 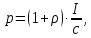 где 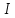 – энергия, падающая на единицу поверхности за единицу времени: – энергия, падающая на единицу поверхности за единицу времени: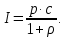 Число фотонов, падающих за 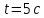 на на 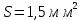 равно: равно: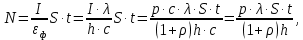 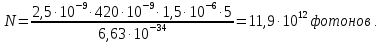 565. Определите максимальную энергию 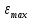 фотона серии Бальмера в спектре излучения атомарного водорода. фотона серии Бальмера в спектре излучения атомарного водорода.Решение: Видимая серия спектра атомарного водорода — это серия Бальмера. Энергия излучения серии Бальмера выражается формулой: 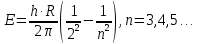 где 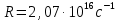 – постоянная Ридберга, – постоянная Ридберга, 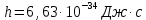 – постоянная Планка. – постоянная Планка. Максимальная энергия будет наблюдаться при больших n, когда: 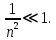 Тогда можно принять: 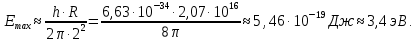 575. Какую ускоряющую разность потенциалов 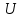 должен пройти протон, чтобы длина волны должен пройти протон, чтобы длина волны  де Бройля была равна: 1) 1 нм; 2) 1 пм? де Бройля была равна: 1) 1 нм; 2) 1 пм?Решение: Импульс протона с заданной длиной волны из соотношения де Бройля:  Кинетическая энергия: 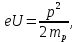 Откуда при 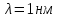 : :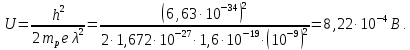 При 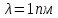 : :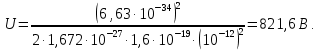 585. Атом испускает фотон с длиной волны  . Продолжительность излучения . Продолжительность излучения 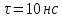 . Определить наибольшую точность . Определить наибольшую точность 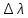 , с которой может быть измерена длина волны излучения. , с которой может быть измерена длина волны излучения.Решение: Энергия фотона:  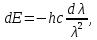 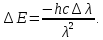 Откуда: 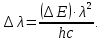 Соотношение неопределенностей Гейзенберга для энергии и времени:    595. Определить образовавшееся ядро в следующей реакции:  Решение: Запишем ядерную реакцию, обозначим через Z и A зарядовое и массовое число неизвестного элемента соответственно:  Из закона сохранения зарядового числа найдем Z: 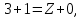  Из закона сохранения массового числа найдем A: 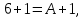 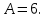 Тогда:  |
