ДР1 теория вероятности. ДР1(тер. вер.) Вариант 3. Студент Бондарев Сергей, гр. РИ-211002. Решение Возможны две гипотезы прибор собран из высококачественных деталей
 Скачать 16.84 Kb. Скачать 16.84 Kb.
|
|
Вариант 3. Студент: Бондарев Сергей, гр. РИ-211002 2. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Известно, что около 40% приборов собирается из высококачественных деталей, при этом вероятность безотказной его работы, за время t равна 0,95. Если прибор собран из деталей обычного качества, эта вероятность равна 0,7. Прибор испытывался в течение времени t и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей. Решение: Возможны две гипотезы: 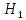 - прибор собран из высококачественных деталей, - прибор собран из высококачественных деталей, - прибор собран из деталей обычного качества. - прибор собран из деталей обычного качества.Вероятность этих гипотез до опыта: 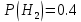 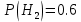 В результате опыта наблюдено событие А-прибор безотказно работал время t. Условные вероятности этого события при гипотезах 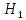 и и  равны: равны: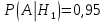  По формуле находим вероятность гипотезы 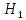 после опыта: после опыта: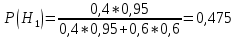 3. В конверте среди 100 фотографий находится одна разыскиваемая. Из конверта наудачу извлекается 10 фотографий. Найти вероятность того, что среди них окажется нужная. Решение: Всего у нас 100 фотографий, вытащить 10 можно 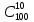 способами, нужных нам среди них наборов (т.е. тех, которые содержат искомую фотографию), будет способами, нужных нам среди них наборов (т.е. тех, которые содержат искомую фотографию), будет 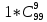 (одна нужная и девять любых из оставшихся 99). (одна нужная и девять любых из оставшихся 99). 4. В кошельке лежат 13 пятикопеечных монет и 7 десятикопеечных. Найти вероятность того, что при извлечении наудачу трех монет из кошелька, они все окажутся десятикопеечными. Решение: Основные событие А-при извлечении наудачу трех монет из кошелька они все окажутся десятикопеечными. По классическому определению вероятности, вероятность события А равна 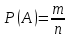 где m- число благоприятных исходов, n- общее число исходов. 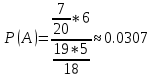 5. Агентство по страхованию автомобилей разделяет водителей по трем классам: №1 (мало рискует), № 2 (рискует средне), № 3 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу № 1, 50% - к классу № 2 и 20% - к классу № 3. Вероятность того, что в течение года водитель класса № 1 попадет хотя бы в одну аварию, равна 0,01, для водителя класса № 2 эта вероятность равна 0,02, а для водителя класса № 3 - 0,08. Найти вероятность того, что водитель, застраховавший свою машину, попадет в аварию в течение года. Решение: A={водитель опадает в аварию}. 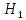 ={водитель относится к №1}, ={водитель относится к №1},  ={водитель относится к №2 }, ={водитель относится к №2 },  ={водитель относится к №3}. ={водитель относится к №3}. ; ;   ; ;   ; ; 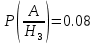 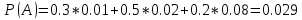 . .По формуле Байеса пересчитаем вероятности гипотез, после того как событие А произошло: 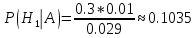 ; ;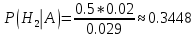 ; ; . .6. При передаче сообщения вероятность искажения одного знака равна 0,1. Найти вероятность того, что сообщение из 10 знаков будет содержать не более трех искажений. Решение: 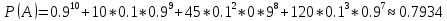 7. На кафедре иностранных языков работает несколько преподавателей. Из них английский язык знают 6 человек, немецкий – 6 человек, французский – 7 человек; причем английский и немецкий знают 4 человека, немецкий и французский – 3 человека, французский и английский – 2 человека, 1 человек знает все три языка. Сколько человек работает на кафедре? Сколько из них знают только английский? Сколько человек знают только 1 язык? Решение: В отделе работают 6+6+7-4-3-2+1=11 человек; 4-1=3 человека знают только английский; Только одним иностранным языком владеют: - только английским 6-4-2+1=1, - только немецким 6-4-3+1=0, - только французским 7-3-2+1=3, 3+1=4 человека знают только один иностранный язык |
