Анализ дискретных систем. Работа. Решение Взаимосвязь угла падения луча на торец стекловолокна с предельным углом п следует из закона преломления
 Скачать 112.01 Kb.
|
|
Задача №1 Имеется оптическое волокно со следующими параметрами nс - абсолютный показатель преломления сердцевины волокна, nо - абсолютный показатель преломления оболочки волокна. Определить предельный (критический) угол ( П ) падения луча на границу раздела сердцевина - оболочка, числовую апертуру оптического волокна (NA), апертурный угол (П ). Значения nс = 1,476, nо = 1,47. 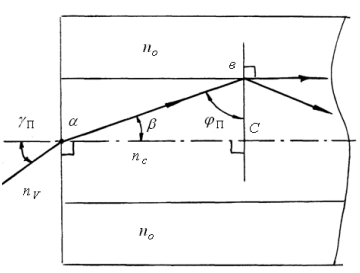 Рисунок 1. – Оптическое волокно. Решение Взаимосвязь угла падения луча на торец стекловолокна с предельным углом п следует из закона преломления:  .Из  abc: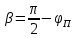 ,  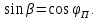Согласно закону преломления, в окрестности точки b   Величина NA носит название номинальной числовой апертуры стекловолокна и является одной из его фундаментальных лучевых характеристик, поскольку определяется только значениями n0 и nc . Угол П называют апертурным углом.  В задаче примем nv=1. Найдем апертурный угол 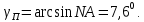 Задача №2  Рисунок 1 - Схема ввода излучения в планарный оптический волновод. Решение Излучение вводится из лазера в планарный оптический волновод с помощью прямоугольной призмы с показателем преломления n4. Определить, каким должен быть угол падения излучения на призму (α), чтобы при распространении излучения по волноводу выполнялось условие полного внутреннего отражения. Исходные данные задачи: n1=1,5, n2=1,46, n4=2, 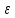 =450.В оптических интегральных схемах (ОИС) волноводы изготавливают следующим образом: на подложку (показатель преломления n2 )наносят тонкую полоску вещества (например, кварца, показатель преломления n1 ), толщиной d. Это и будет волновод. При этом волновод с одной стороны будет граничить с подложкой, с остальных – с воздухом (n3 ). Причем, для выполнения условия полного внутреннего отражения n1 >n2 и n1 >n3 . Такой оптический волновод называется ПЛАНАРНЫМ.  Рисунок 2 - Планарный оптический волновод. Рассмотрим границу раздела волновод-подложка ( 𝑛2– 𝑛1). Запишем для данной границы раздела условие полного внутреннего отражения (найдем критический угол падения на границу раздела):  Аналогично найдем условие полного внутреннего раздела для границы раздела 𝑛1(волновод)– воздух(𝑛3): Т.к. 𝑛2 > 𝑛3, то в любом случае  => При любом 𝜑 >=  будет наблюдаться явление Полного Внутреннего Отражения при распространении по такому оптическому световоду.Обозначим 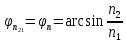 Запишем закон преломления для границы раздела волновод-призма:   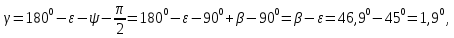 Запишем закон преломления для границы раздела воздух – призма:  Задача №3 На дифракционную решетку (ДР) с числом рабочих щелей N и периодом решетки, равным d мкм, падает сигнал, содержащий 2 длины волны: λ1 и λ2. Определить минимально возможную разницу длин волн, которые могут быть разделены данной дифракционной решеткой. Рассчитать угловую и линейную дисперсии данной решетки. Определить разрешающую способность решетки, считая, что максимальная длина волны спектрального диапазона, падающего на решетку, соответствует λ2. Считая, что расстояние до экрана равно r, см, определить расстояние между максимумами 1-го порядка, соответствующими длинам волн λ1 и λ2. Исходные данные к задаче № 3 Рабочее число щелей – 100, Период ДР, d = 6 мкм,  = 0,4 мкм,  = 0,6 мкм,r = 10 см. Решение Минимально возможная разница длин волн, которые могут быть разделены данной дифракционной решеткой, определяется критерием Рэлея: 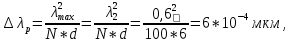 Разрешающая способность дифракционной решетки, в свою очередь, определяется как 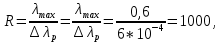 Для определения угловой дисперсии дифракционной решетки можно воспользоваться разными способами. Например, исходя из условий главных максимумов:  Найдем углы φ1 и φ2, соответствующие максимумам 1-го порядка длин волн λ1 и λ2:   , и рассчитаем затем угловую дисперсию, как:  Где   Угловую дисперсию рассчитаем так:  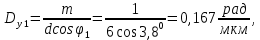  Линейную дисперсию найдем так:    Расстояние между максимумами выразим формулы:  Тогда  Задача 4 Определить уровень мощности и мощность сигнала на выходе оптического волокна (ОВ), а также мощность сигнала на входе оптического волокна длиной L км, если уровень мощности сигнала на передаче (на входе ОВ) равен ps, дБм, коэффициент затухание оптического волокна равен α, дБ/км. Рассчитайте коэффициент поглощения оптического волокна β, 1/км. Исходные данные к задаче: Длина оптического волокна L = 45 км, коэффициент затухания ОВ  = 0,4 дБ/км, ps = -3 дБм.Решение Определяем затухание оптического волокна длиной L:  Находим уровень мощности на выходе оптического волокна: 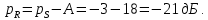 Переводим уровни мощности на входе и выходе оптического волокна в мощность, по формуле:   Рассчитываем коэффициент поглощения ОВ β из соотношения:  Задача 5 Определить пороговый коэффициент усиления ППЛ с РФП, излучающего длину волны λ0, соответствующий значению порогового тока, если коэффициент поглощения активного слоя равен α, показатель преломления активного слоя равен n, а длина резонатора активного слоя равна L. Рассчитать углы расходимости излучения этого ППЛ, если размеры активной области равны LxWxd. Определить основные параметры спектра ППЛ с РФП: число мод в спектре, расстояние между соседними модами, ширину спектра моды и добротность основной моды резонатора, качество резонатора. Привести спектр ППЛ с РФП. Исходные данные к задаче: 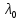 = 0,85 мкм, n = 3,2, L = 300 мкм, W = 50 мкм,d = 5 мкм, α = 12 1/см,  Решение Пороговый коэффициент усиления определяем из порогового условия генерации ППЛ ( условия баланса амплитуд) (раздел «Источники излучения»):  где - коэффициент поглощения активной области (переведем 1/см в 1/м); L – длина резонатора Фабри-Перо; R1, R2 – коэффициенты отражения зеркал.Считая, что коэффициенты отражения зеркал одинаковы и равны  Условие баланса амплитуд преобразуем к виду:  Углы расходимости излучения ППЛ определим по следующей дифракционной формуле:   Расстояние между модами определим из соотношения:  Добротность резонатора на центральной моде 0 определим из соотношения:  Число мод в интервале 0,5 определим:  Добротность основной моды резонатора можно определить по формуле:  Ширину спектра моды резонатора (Δλm) можно определить из соотношения:  Качество РФП рассчитаем по формуле:   Рисунок 1 - Спектральная характеристика ППЛ с РФП. Задача 6 Рассчитать квантовую эффективность фотодиода на заданной длине волны λ, если ширина области поглощения W, мкм, а коэффициент поглощения материала соответствует заданной длине волны. Рассчитать чувствительность заданного фотодиода. Определить фототок при данной мощности излучения, падающей в зрачок фотодиода, если известна мощность излучения на выходе передатчика ps и затухание линии связи А. Данные к задаче: ФД – p-i-n, материал – Si, λ = 0,85 мкм, W = 50 мкм, ps = -3 дБм, А = 24 дБ. Решение Квантовая эффективность фотодиода соответствует величине: η = 1-exp(-αW)=0,97. Где α = 700 см-1 = 70000 м-1 – коэффициент поглощения материала, определяется по графику рис.6.1 для нашего материала и заданной длины волны. При расчете η переведите единицы измерения из см-1 в м -1 (умножить на 100). W- ширина области поглощения (i-области). Чувствительность фотодиода зависит от его типа и может быть определена по формулам: - для p-i-n ФД:  - для ЛФД: 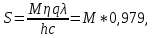 Где q=1.6*10-19, Кл – заряд электрона, h=6,626*10-34, Дж*с – постоянная Планка, с=3*108, м/с – скорость света, М – коэффициент лавинного умножения ЛФД. Фототок найдем по формуле: Ip=SPin=1,958 мкА, Где Рin – мощность, падающая в зрачок фотодиода. Для нахождения мощности, падающей в зрачок фотодиода воспользуемся соотношениями, приведенными в задаче 4. Находим уровень мощности на выходе оптического волокна:   Найденную мощность следует представить в мкВт, а фототок – в мкА. |