РГР Логистика. РГР_М_1_. Решение задач линейного программирования в пакетах Mathcad и ms excel
 Скачать 1.5 Mb.
|
Лабораторная работа 1. Решение задач линейного программирования в пакетах MathCAD и MS Excel.Задачи линейного программирования (ЛП) являются математическими моделями многих практических задач, возникающих в экономике, планировании, управлении и других областях. Кроме того, в ряде случаев решение задачи линейного программирования является этапом решения более сложной задачи оптимизации (например, задачи целочисленного линейного программирования) [1,3,6,7]. Под задачей линейного программирования понимается задача поиска решения  , которое удовлетворяет системе линейных равенств или неравенств и на котором достигается максимальное или минимальное значение линейной целевой функции f(x).Общая постановка задачи ЛП:  где под знаком “#” понимается любой из знаков “≤”, “≥” и “=”, причем в одной задаче ЛП могут встречаться знаки всех трех типов. Классическим примером содержательной задачи, математической моделью которой является задача линейного программирования, служит задача оптимального планирования производства. Для решения задач ЛП малой и средней размерности (десятки и сотни переменных) используются стандартные программные продукты. Для решения задач ЛП большой размерности (тысячи переменных) требуется разработка специального программного обеспечения. Далее рассмотрим решение задач ЛП в пакетах MathCAD [5] и MS Excel [4] на примере задачи с двумя переменными, которые, без ограничения общности, будем обозначать x и y. Решение задачи ЛП в пакете MathCAD. Требуется найти максимум целевой функции f (x,y) = 4x + 2y при ограничениях 2x + 3y ≤ 18, -x + 3y ≤ 9, 2x - y ≤ 10, x 0, y 0. Прежде чем записать условие задачи в MathCAD, требуется установить режим автоматических вычислений (см. рис. 1).  Рис.1 Выбор режима «Автоматическое вычисление» Далее необходимо выполнить следующие действия: 1) записать целевую функцию; 2) присвоить переменным x и y произвольные (допустимые) значения; 3) после зарезервированного слова Given записать ограничения задачи; 4) с помощью функции Maximize (Minimize - для задачи на минимум) найти оптимальный вектор z =(z0, z 1) = (x,y) и значение функции на этом векторе. Ниже приведен фрагмент рабочего документа MathCAD. f (x,y): = 4x + 2y x:=1 y:=1 Given 2x + 3y ≤ 18 -x + 3y ≤ 9 2x - y ≤ 10 x 0y 0 Z:= Maximize(f,x,y)  f(z0, z 1)=28Решение задачи линейного программирования в MicrosoftExcel. Рассмотрим решение той же задачи ЛП f (x) = 4x + 2y max, 2x + 3y ≤ 18, -x + 3y ≤ 9, 2x - y ≤ 10, x 0, y 0. Сначала выделим ячейки под значения под значения переменных x и y, например, ячейки С3 и С4. Далее в ячейку С6 введем целевую функцию = 4*С3 + 2*С4. В ячейки В9 : В11 введем левые части ограничений = 2*C3 + 3*C4, = - 1*C3 + 3*C4, = 2*C3 - 1*C4, а в ячейки С9 : С11 – правые части ограничений (см. рис.2).  Рис. 2. Диапазоны, отведенные под переменные, целевую функцию и ограничения. После этого выберем в главном меню команду Сервис,_Поиск_решения.'>Сервис, Поиск решения. Если в меню Сервис этого пункта нет, нужно установить надстройку. Для этого выберем в меню Сервис пункт Надстройки. В диалоговом окне "Надстройки" нужно найти в списке надстроек "Поиск решения" и установить слева от него флажок. Загрузится Решатель. В дальнейшем при запуске Ехсеl Решатель будет загружаться автоматически, пока не будет снят флажок в окне "Надстройки". Заполним открывшееся диалоговое окно Поиск решения, как показано на рис. 3. 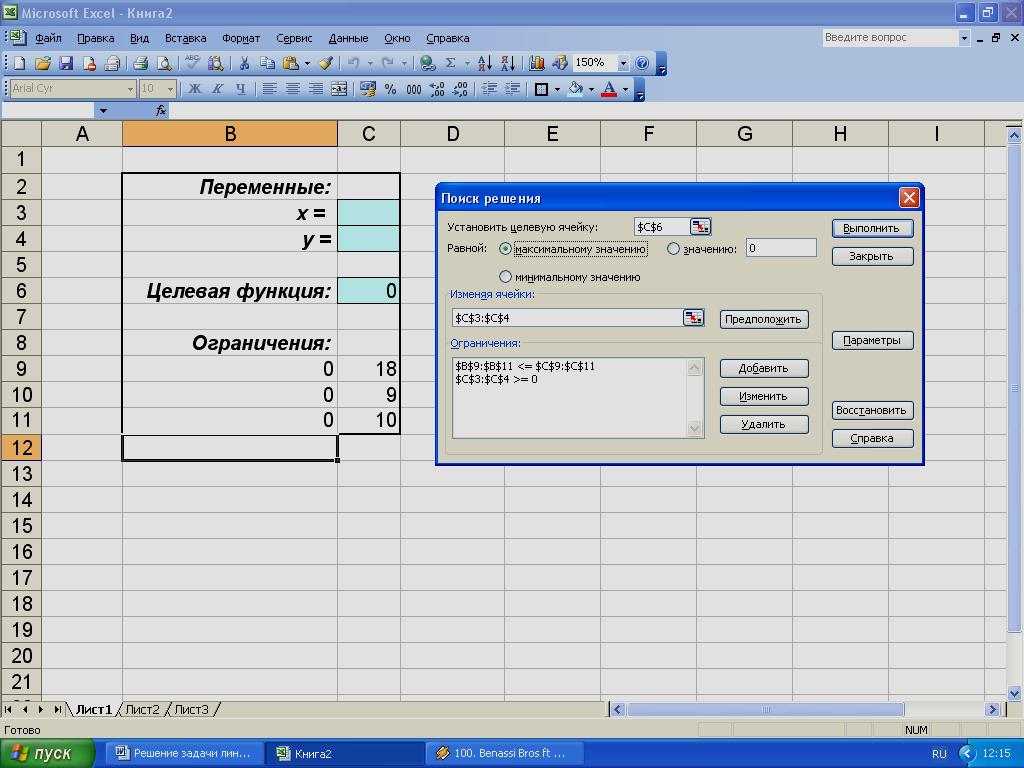 Рис. 3. Диалоговое окно Поиск решений. После нажатия на кнопку Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).  Рис.4. Диалоговое окно Результатыпоиска решения. Оптимальное решение находится в ячейках C3 и C4, а оптимальное значение целевой функции – в ячейке C6 (рис. 5).  Рис.5. Результаты решения. Задачи ЛП в общем случае решаются аналогично в обоих пакетах. |