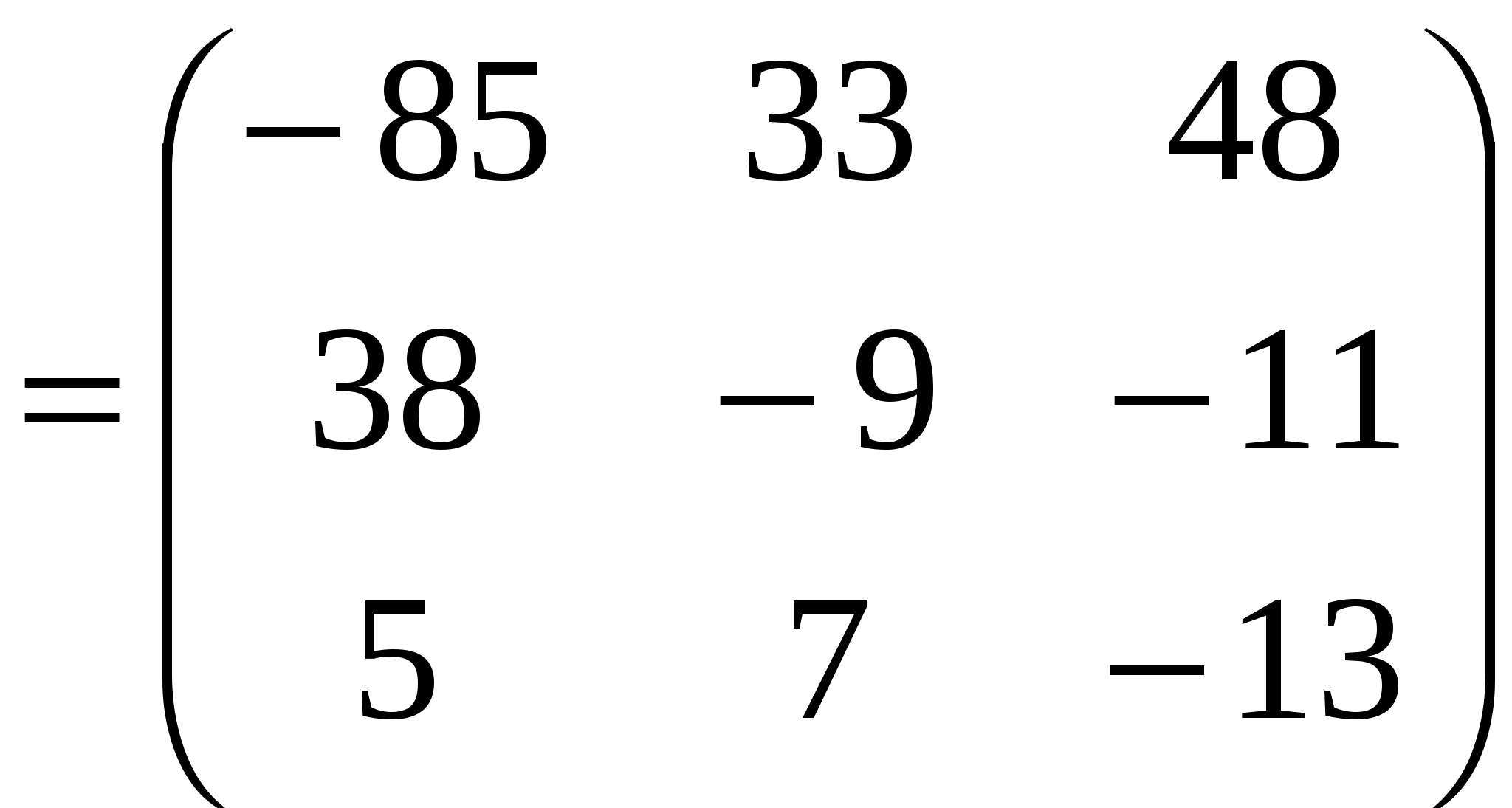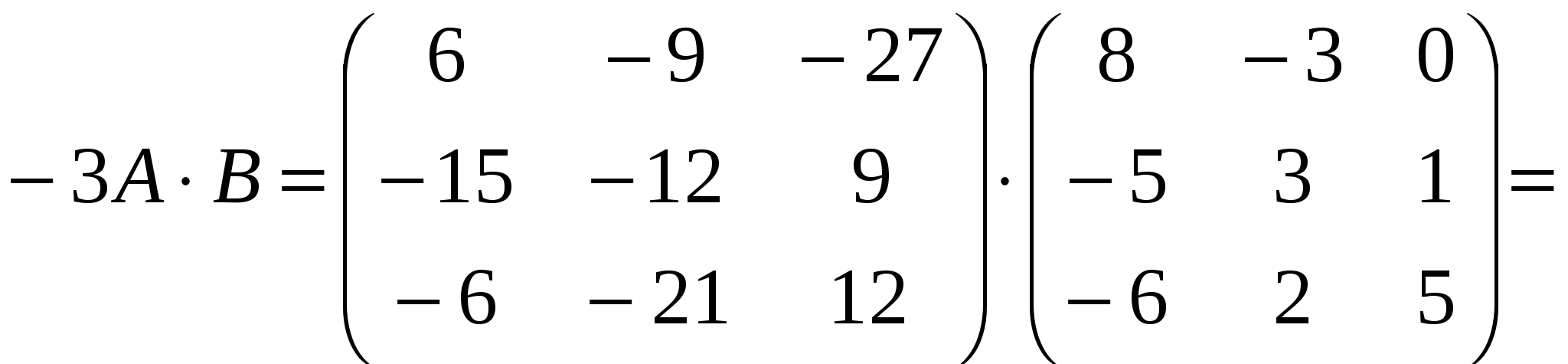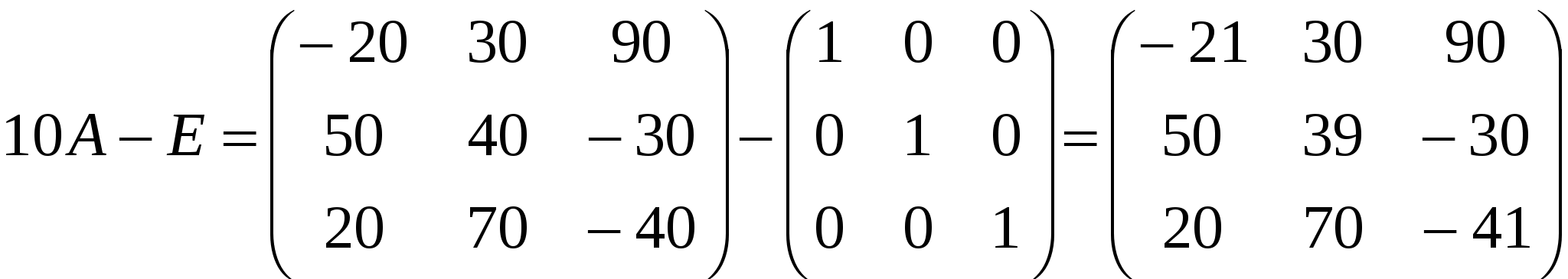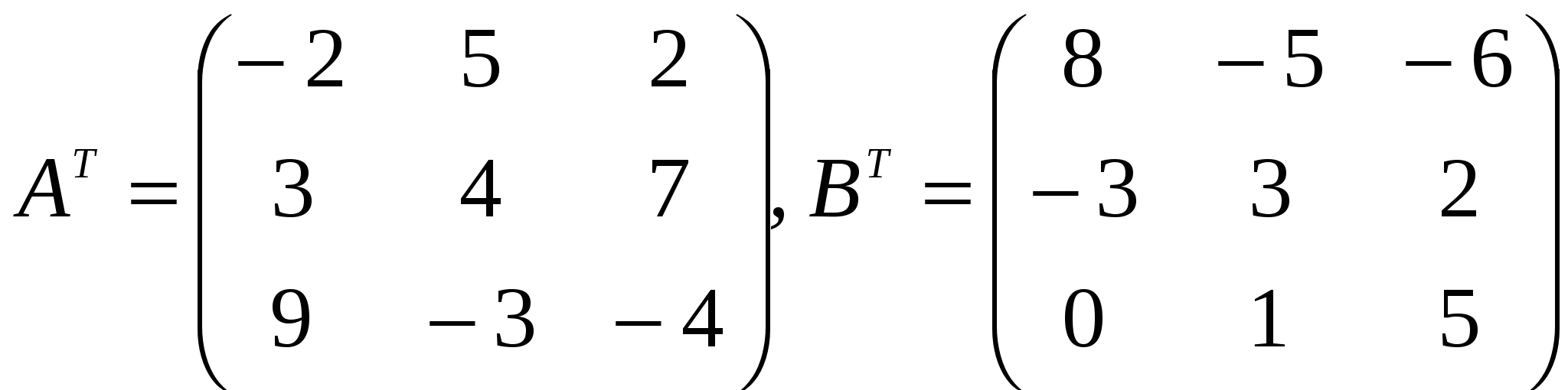линейная алгебра 9 вариант. Решение Задание 2
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Контрольная работа по дисциплине Линейная алгебра и аналитическая геометрия Вариант №9 Задание №1 Для заданных матриц А и В и заданных чисел α и β требуется найти:
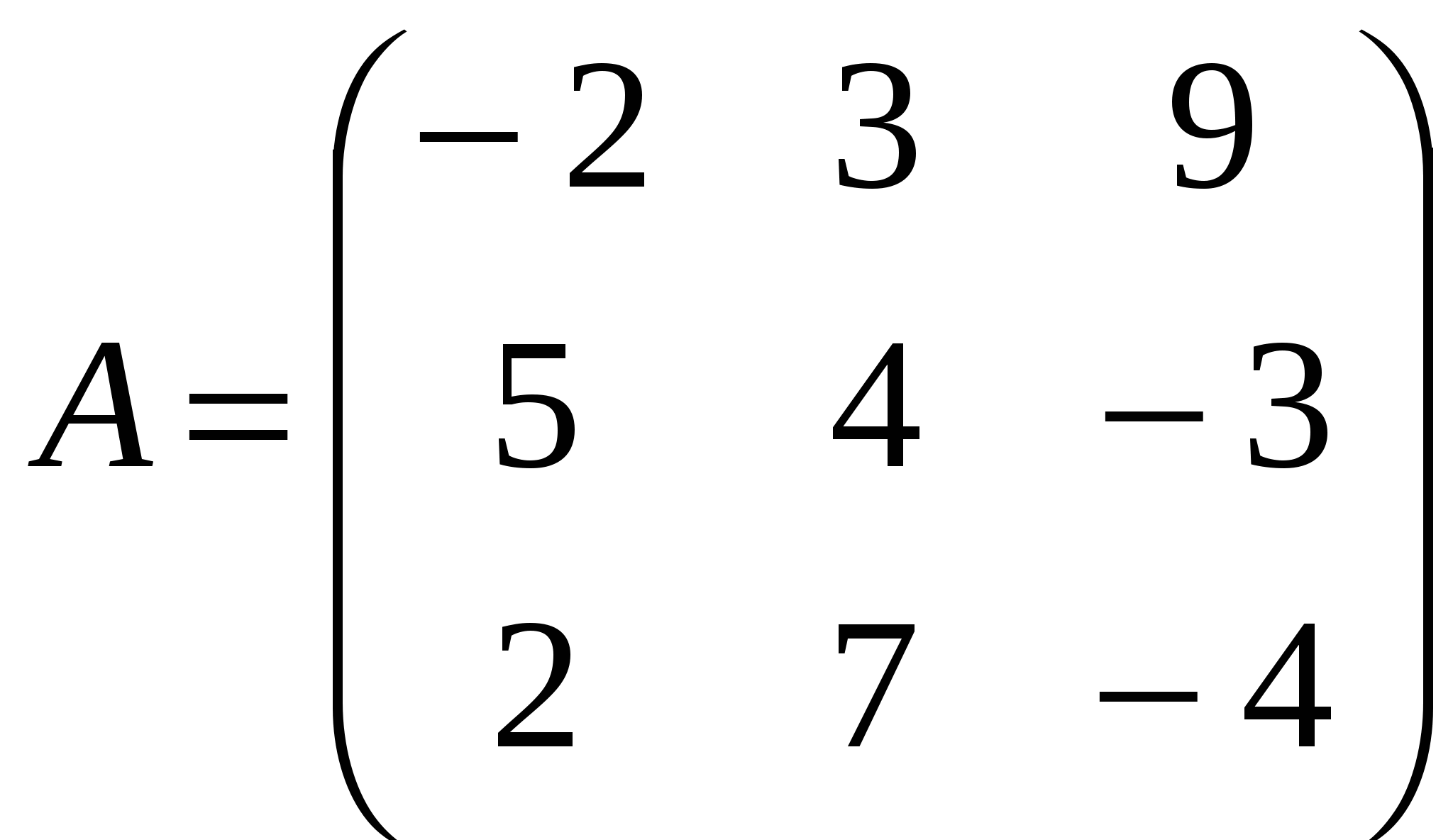 , , 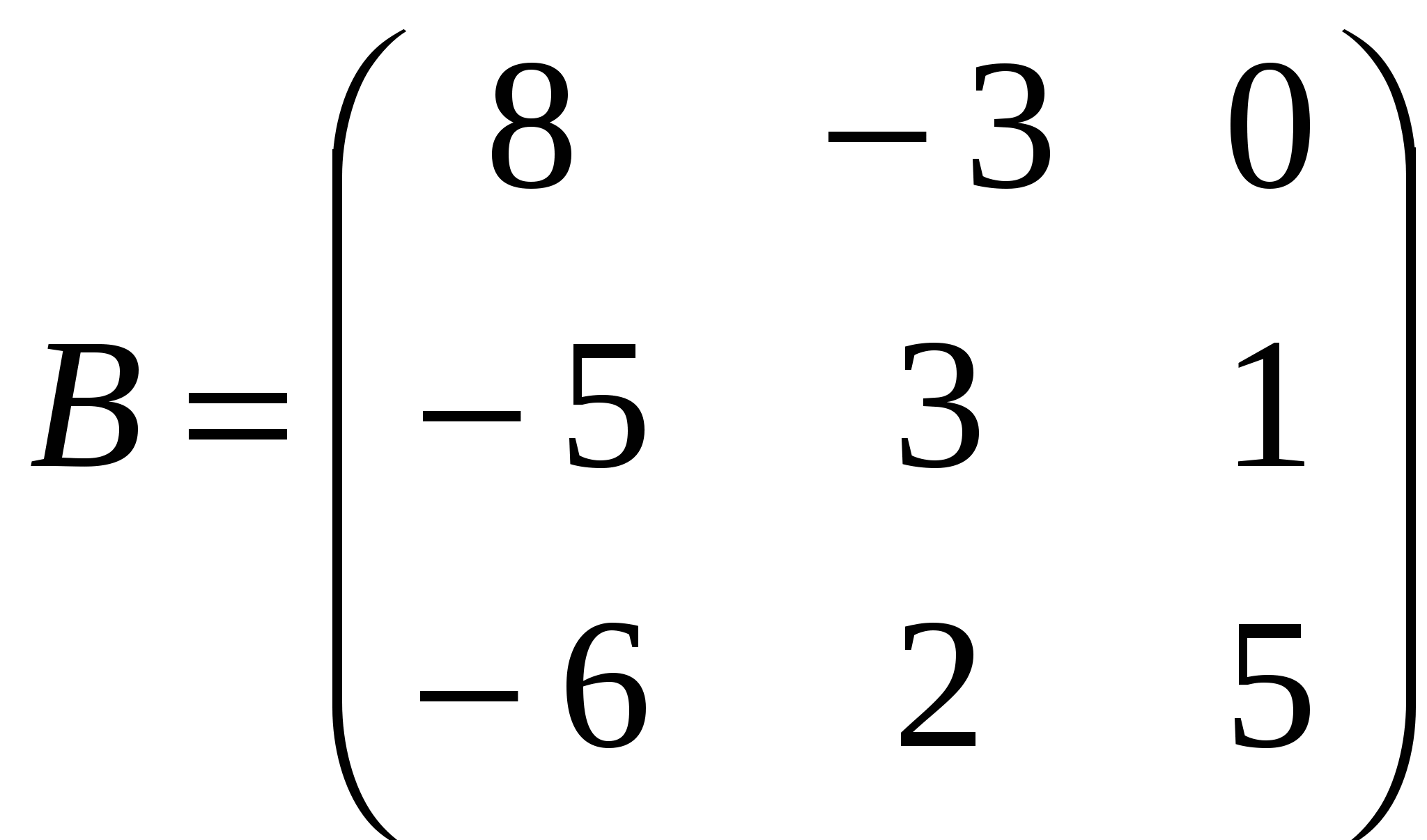 , , Решение: 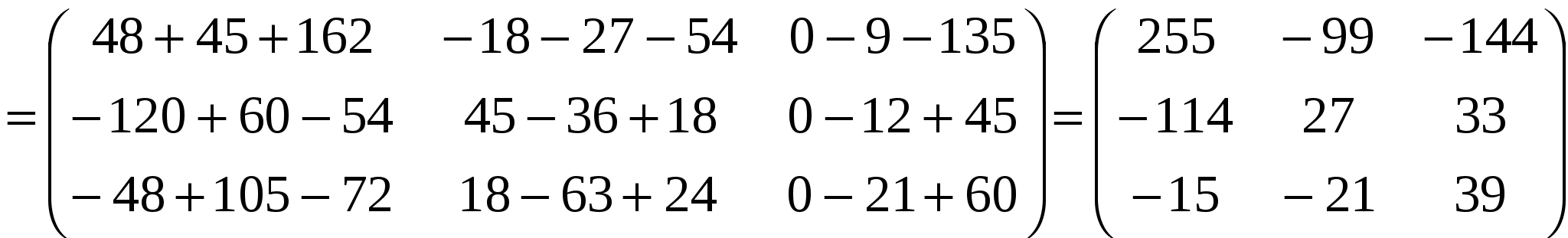 Задание №2 По данной матрице вычислить её определитель следующими способами:
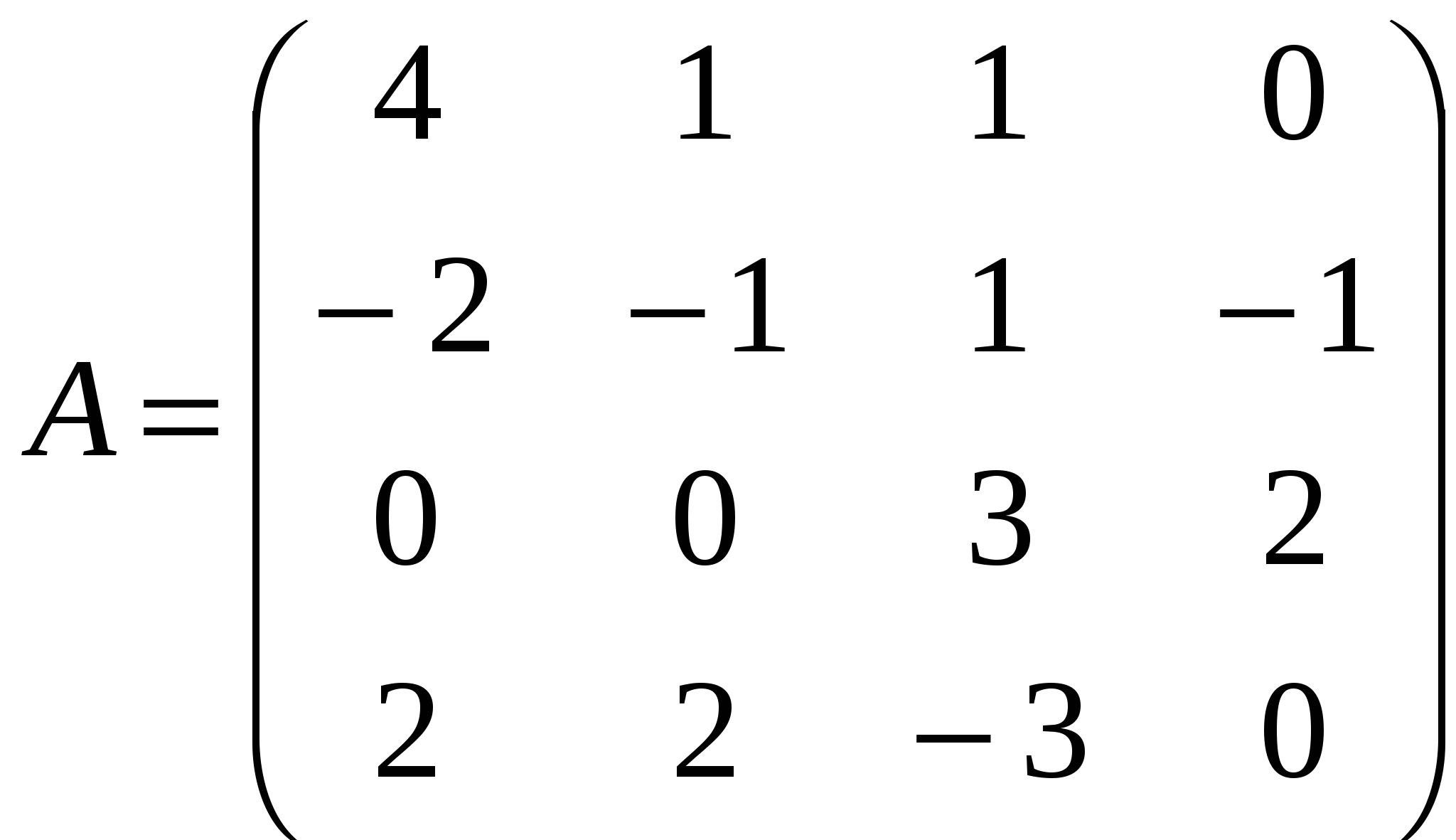 Решение: Разложение по первой строке:  Разложение по первому столбцу 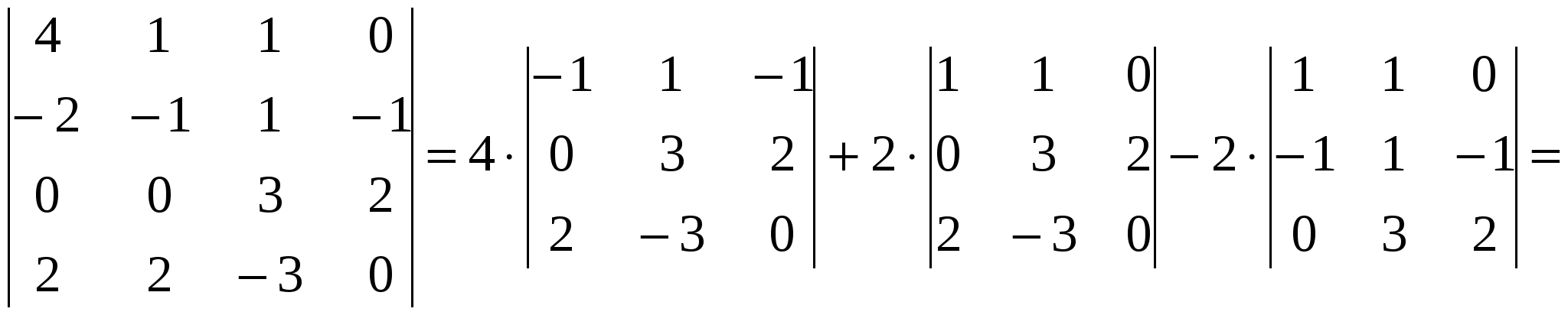 Метод Гаусса 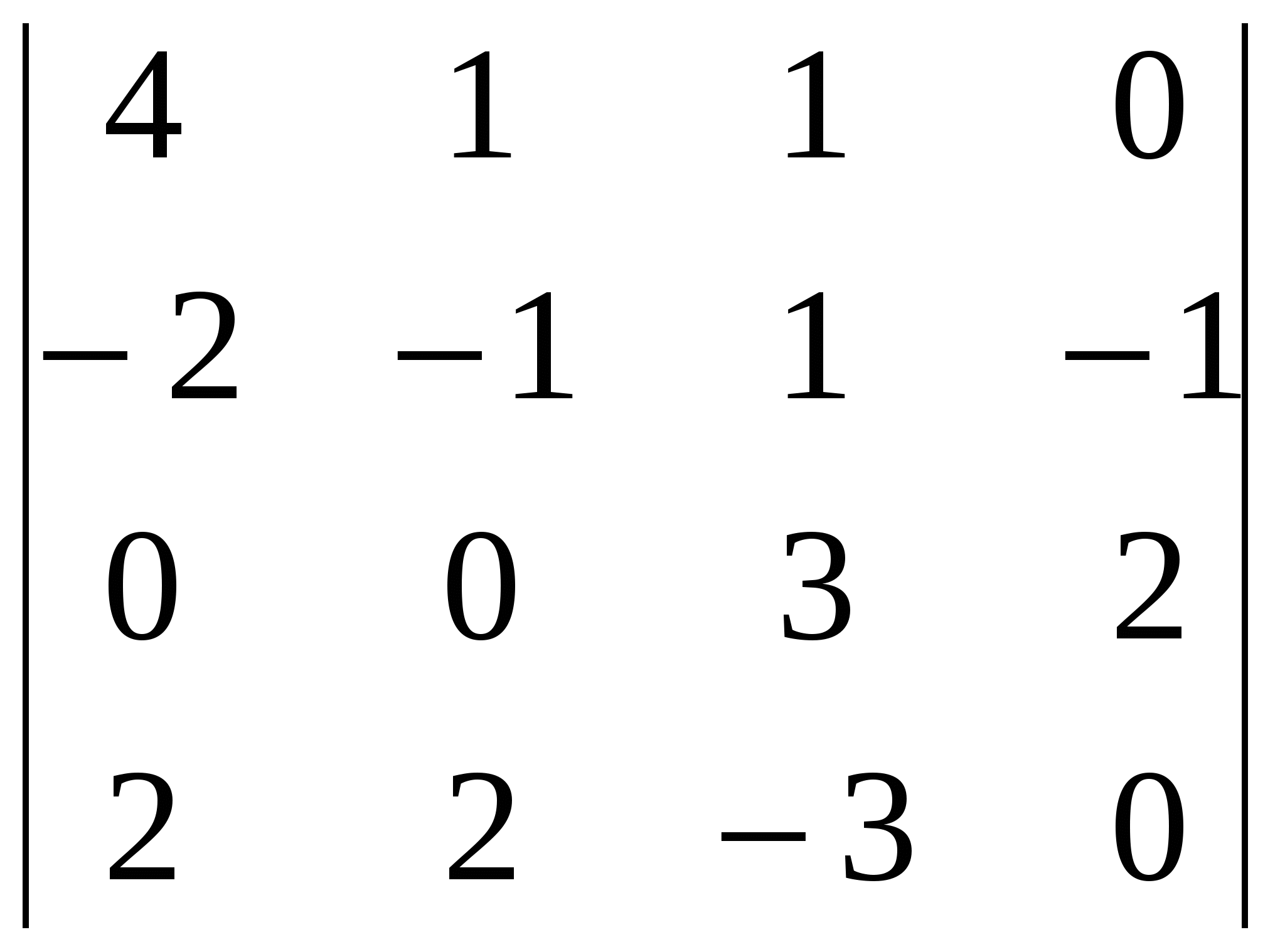 . Ко второй строке добавляем первую строку, умноженную на 0,5 . Ко второй строке добавляем первую строку, умноженную на 0,5 . К четвертой строке добавляем первую, умноженную на 0,5. . К четвертой строке добавляем первую, умноженную на 0,5. 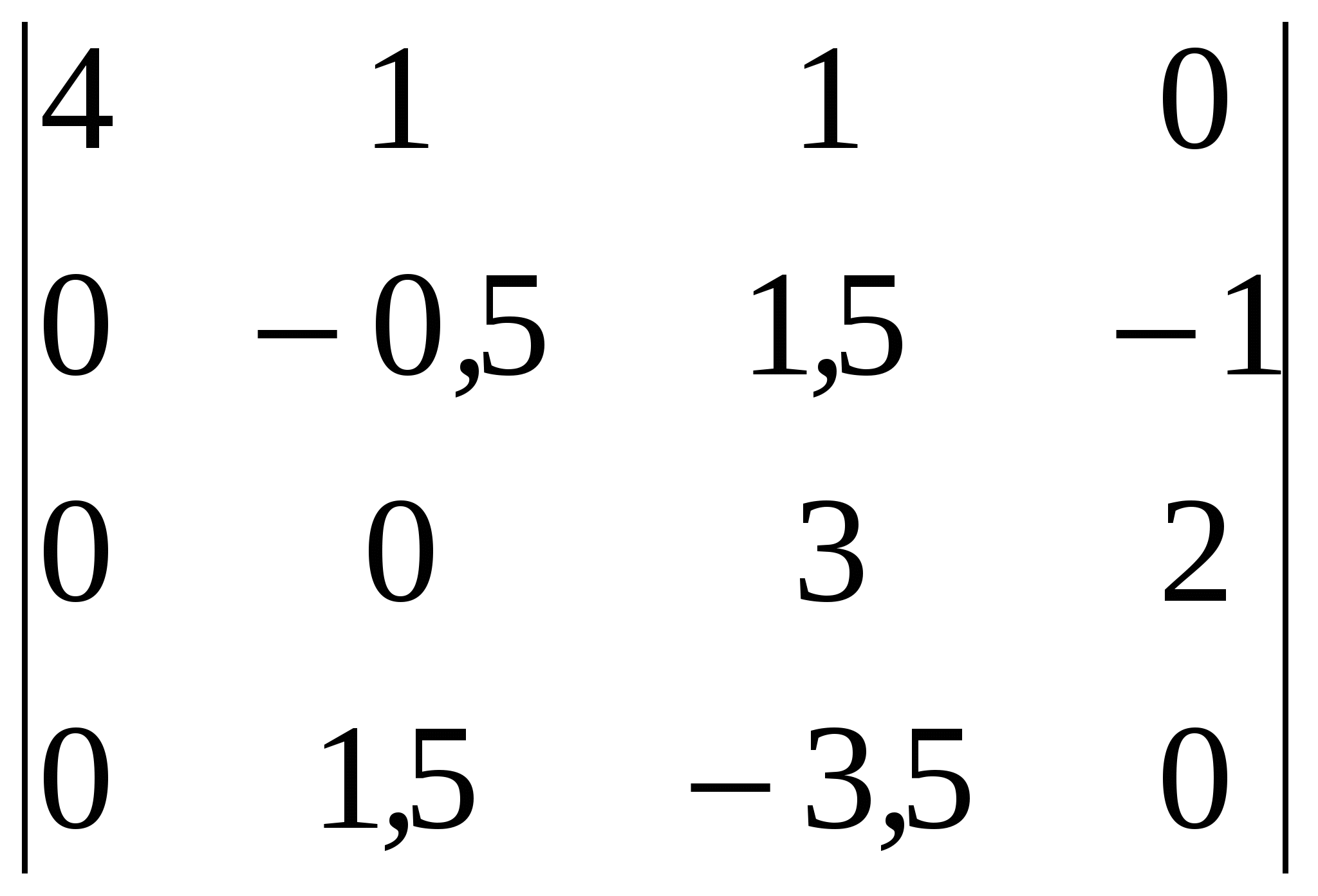 . К четвертой строке добавляем вторую, умноженную на 3 . К четвертой строке добавляем вторую, умноженную на 3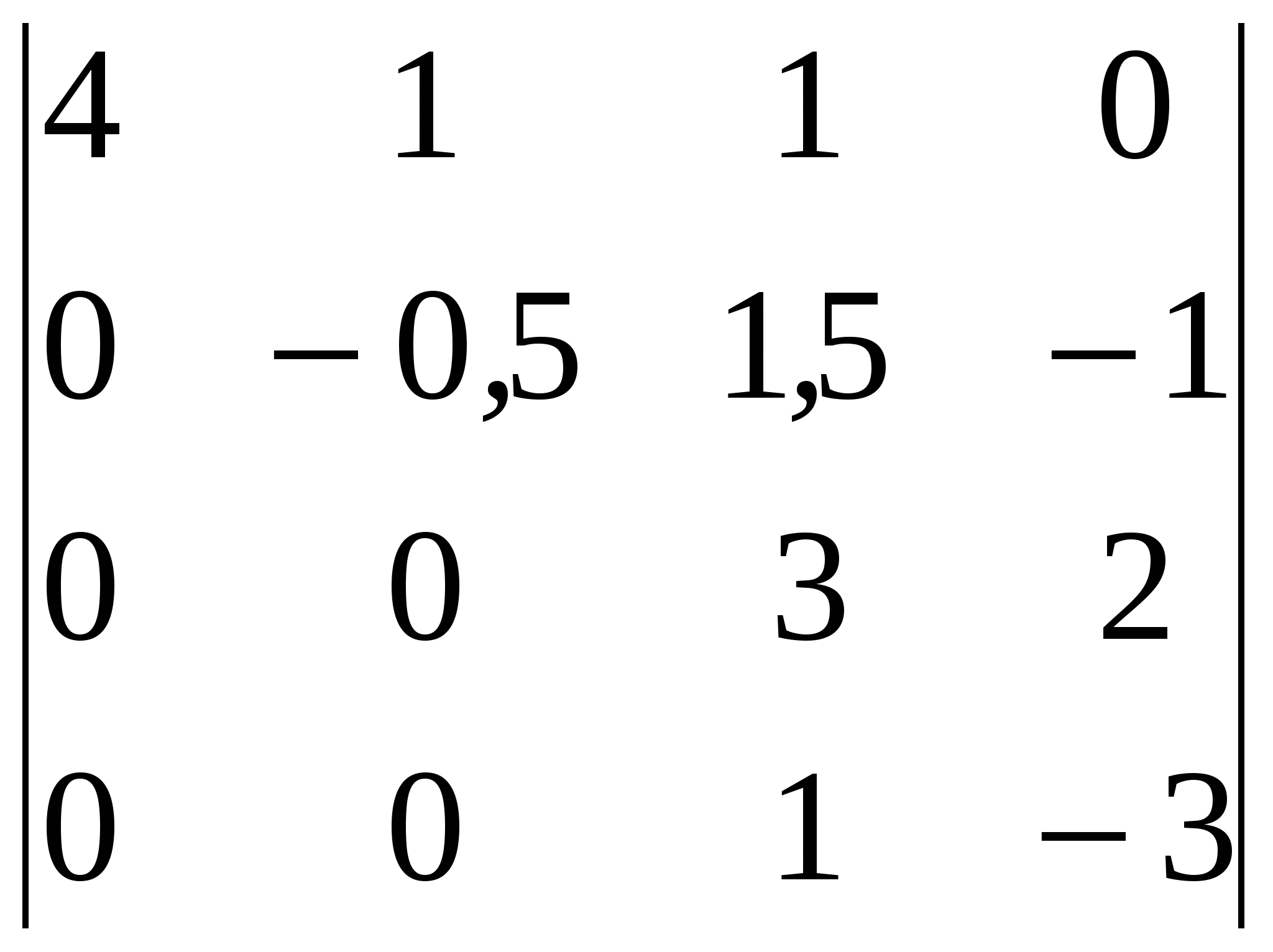 . От четвертой строки отнимаем третью, умноженную на 1/3 . От четвертой строки отнимаем третью, умноженную на 1/3 Ответ: 22 Задание №3 По заданной матрице А найти её обратную А-1 и проверить равенства: А∙А-1=А-1∙А=Е. 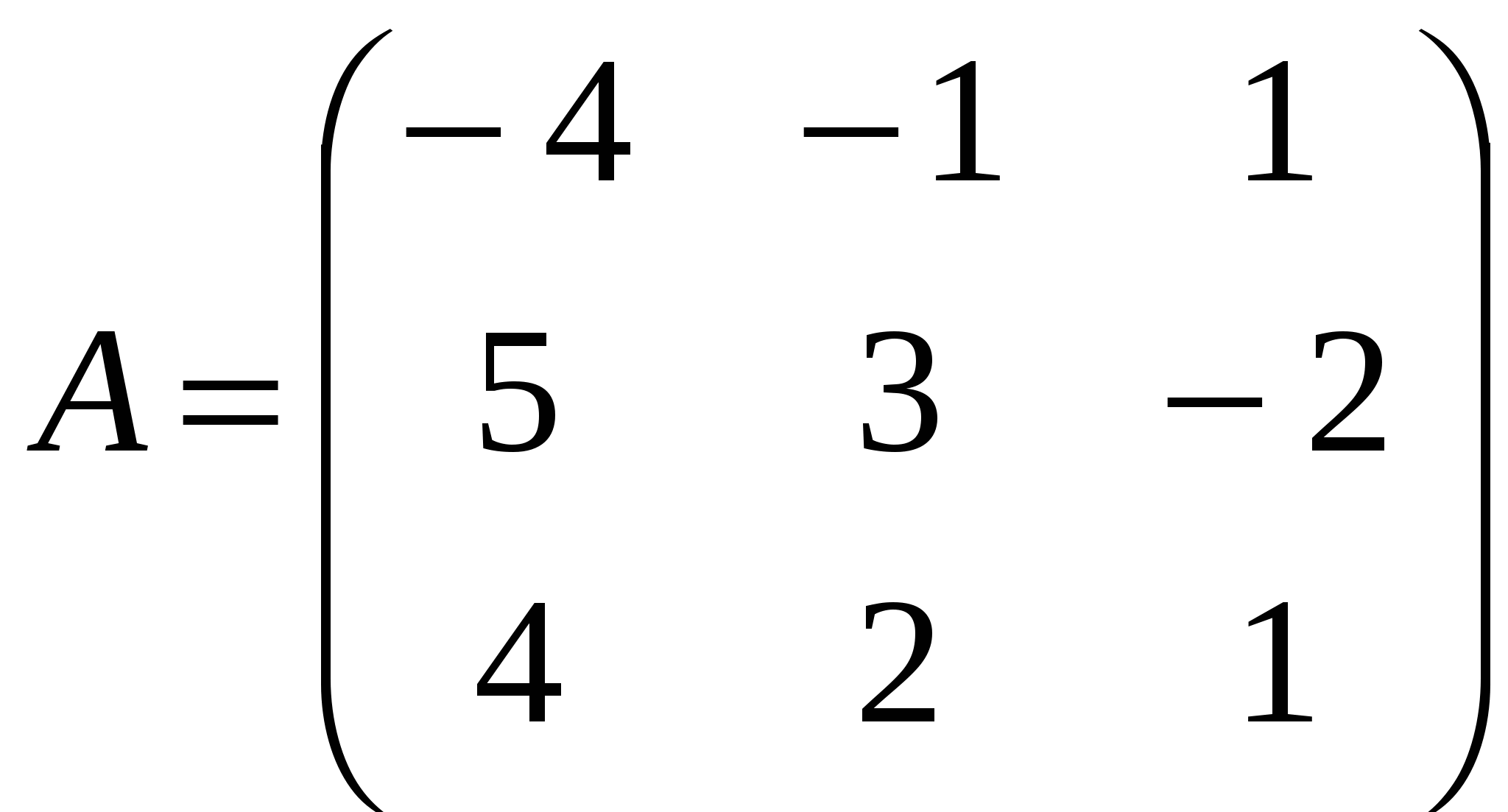 Решение: Находим обратную матрицу матрицы А по формуле:  , ,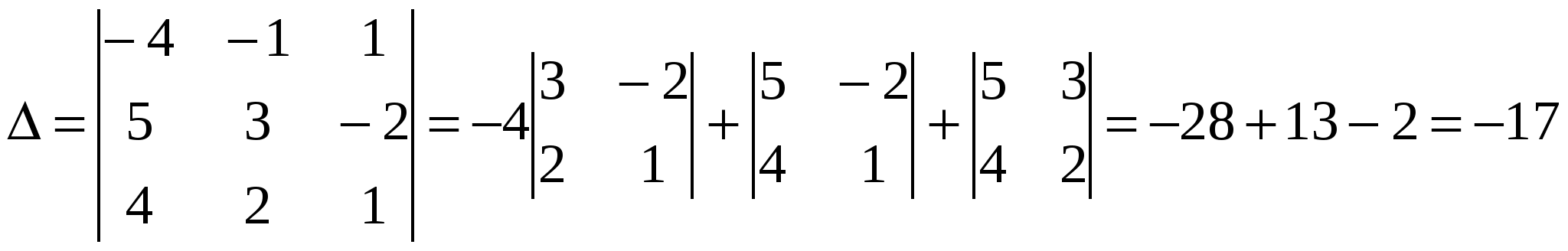 Отсюда 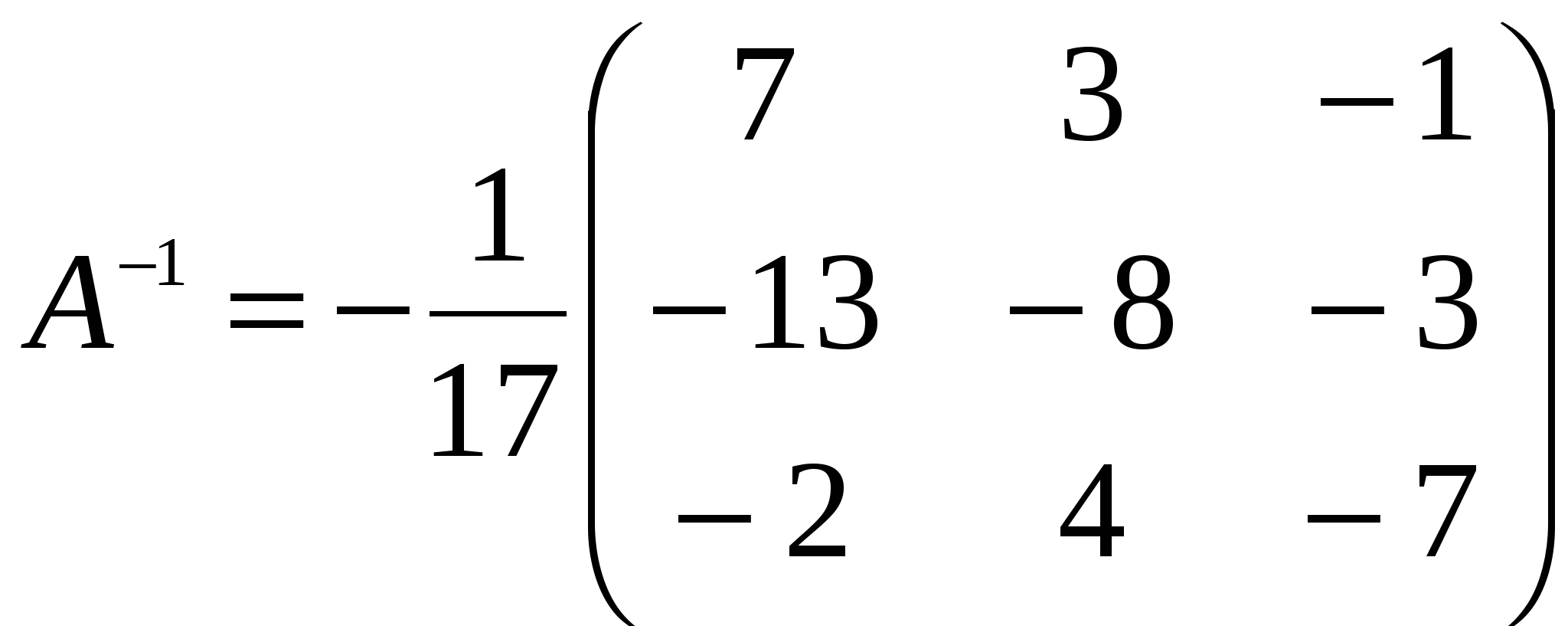 . . Проверим равенство:  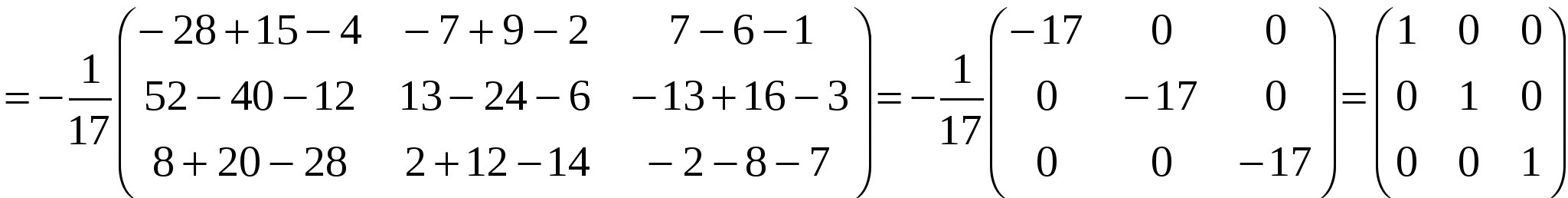 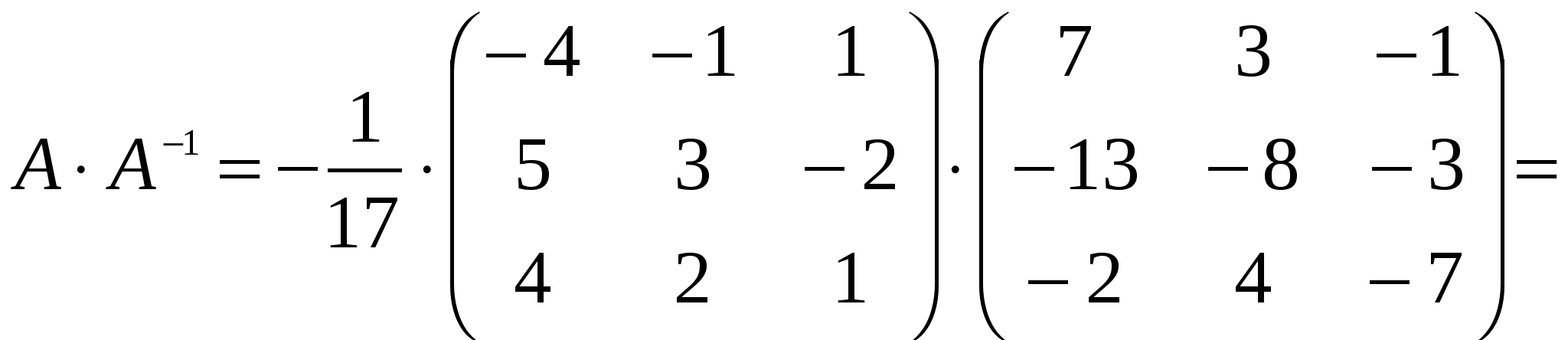 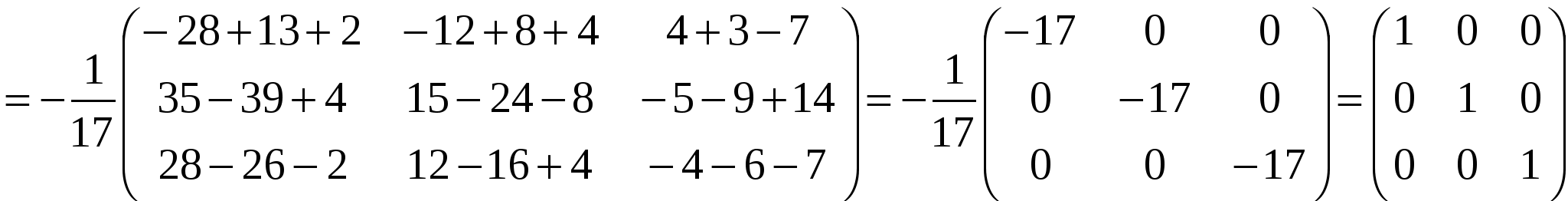 Задание №4 При заданных матрицах А и В найти неизвестную матрицу Х, удовлетворяющую уравнению АХ=В. Задание №5 Вычислить ранг заданной матрицы 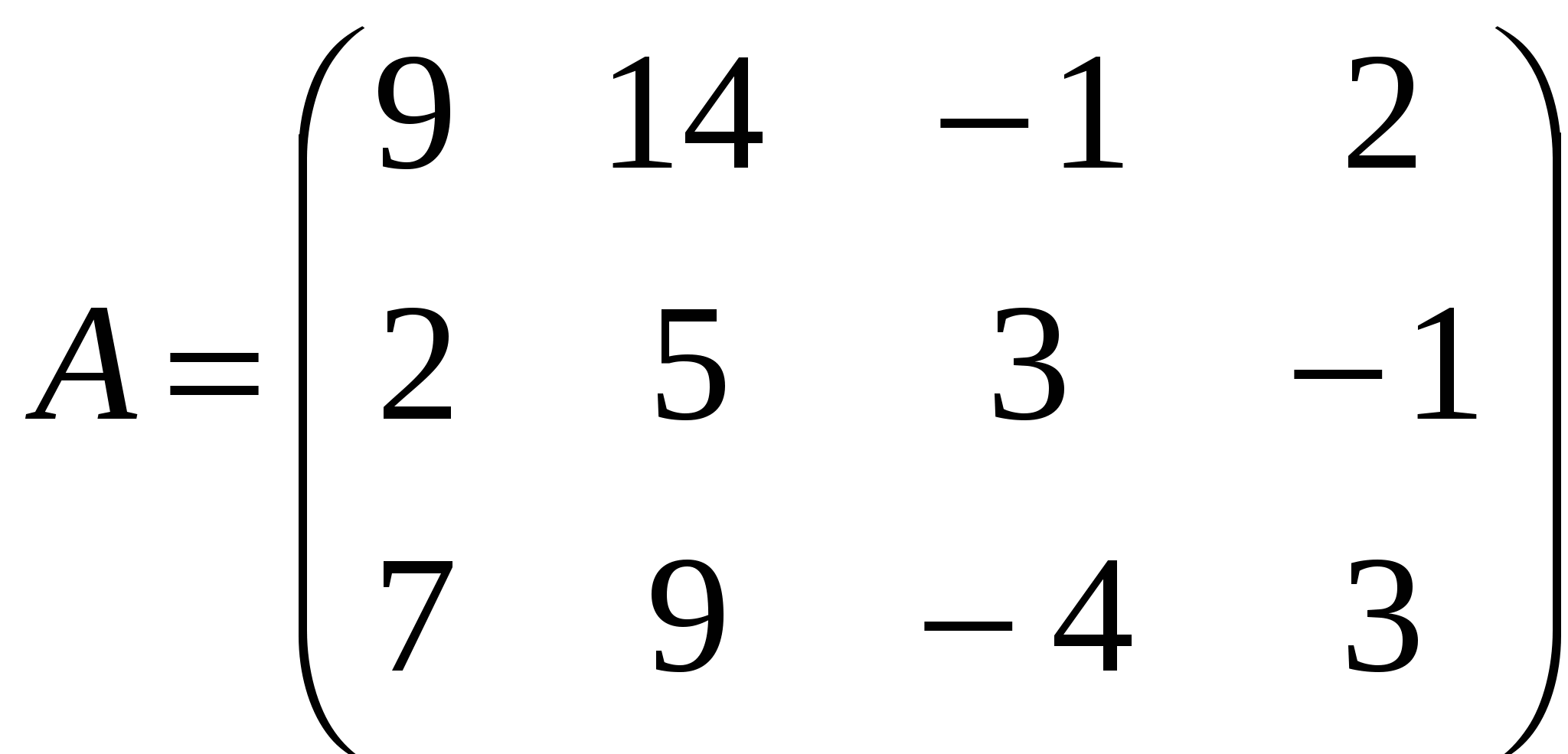 Решение: Сделаем элементарные преобразования матрица А, сложим вторую и третью строки, получим: 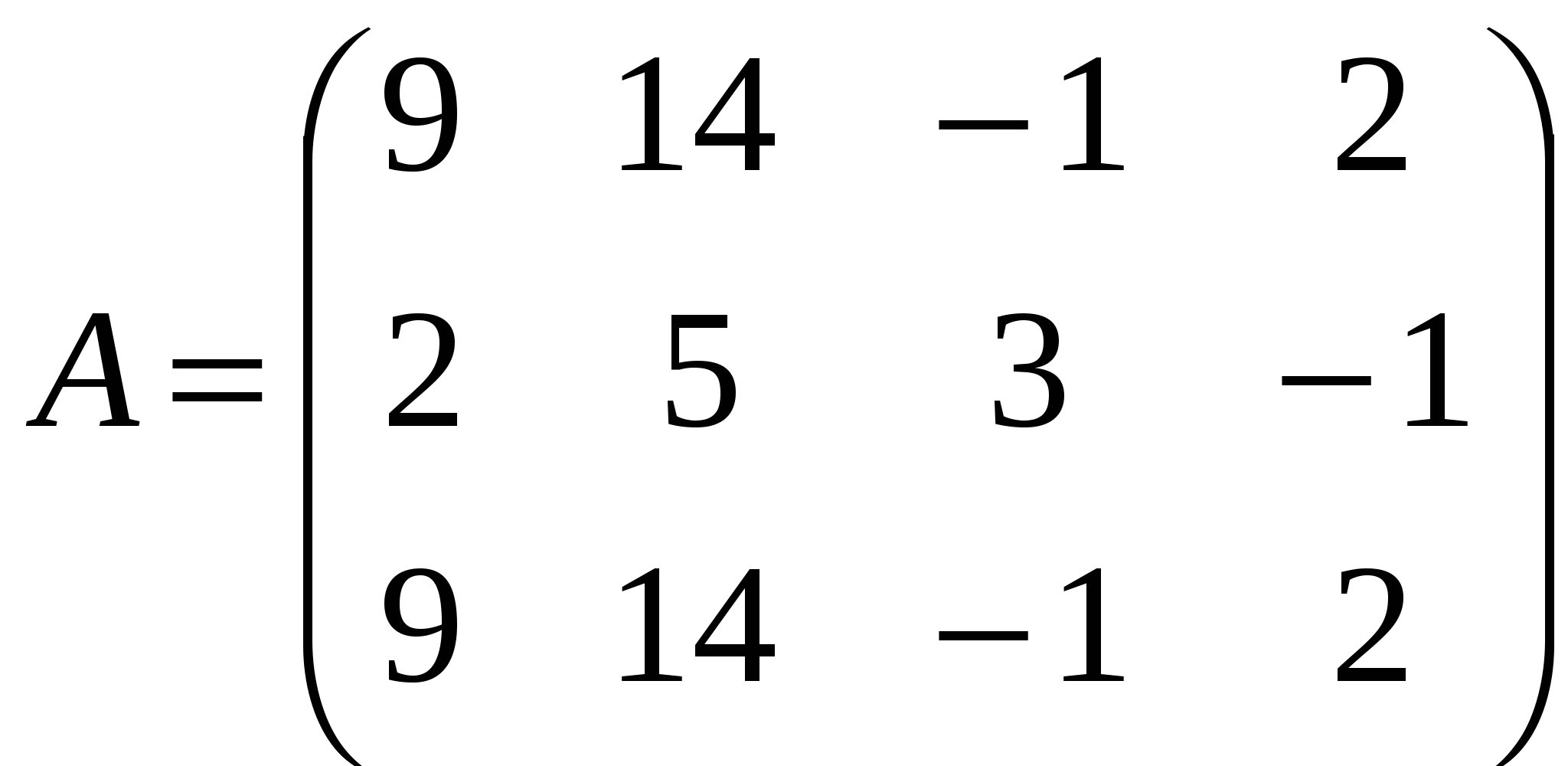 . Вычтем первую и третью строки, получим . Вычтем первую и третью строки, получим . Подсчитаем количество линейно независимых строк данной матрицы, (количество ненулевых строк) это и есть ранг. Таким образом, ранг равен 2. . Подсчитаем количество линейно независимых строк данной матрицы, (количество ненулевых строк) это и есть ранг. Таким образом, ранг равен 2.Ответ: 2 Задание №6 Заданную систему линейных уравнений исследовать на совместность по критерию совместности (по теореме Кронекера-Капелли) и на определённость. 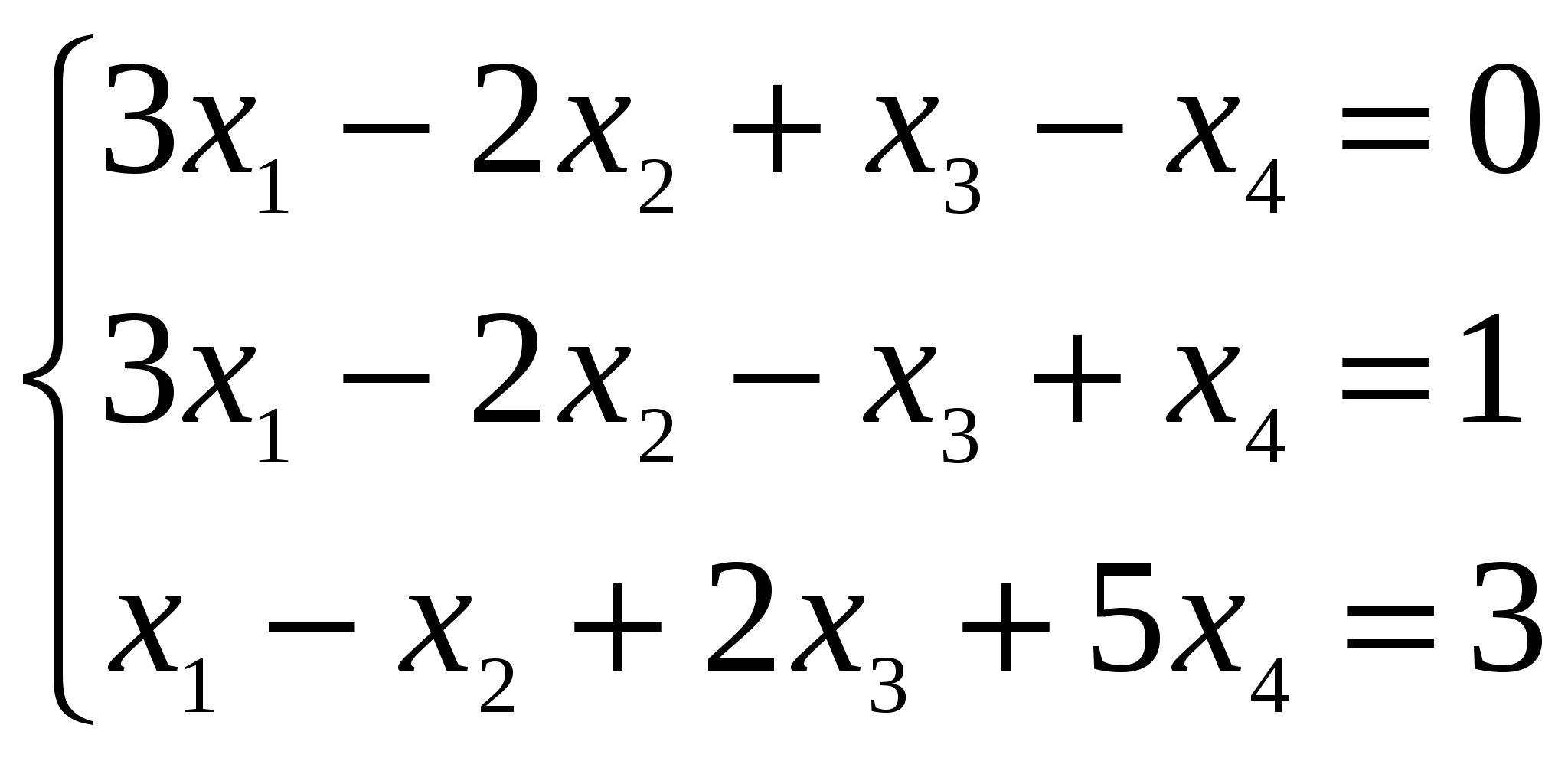 Выпишем основную и расширенную матрицу системы: 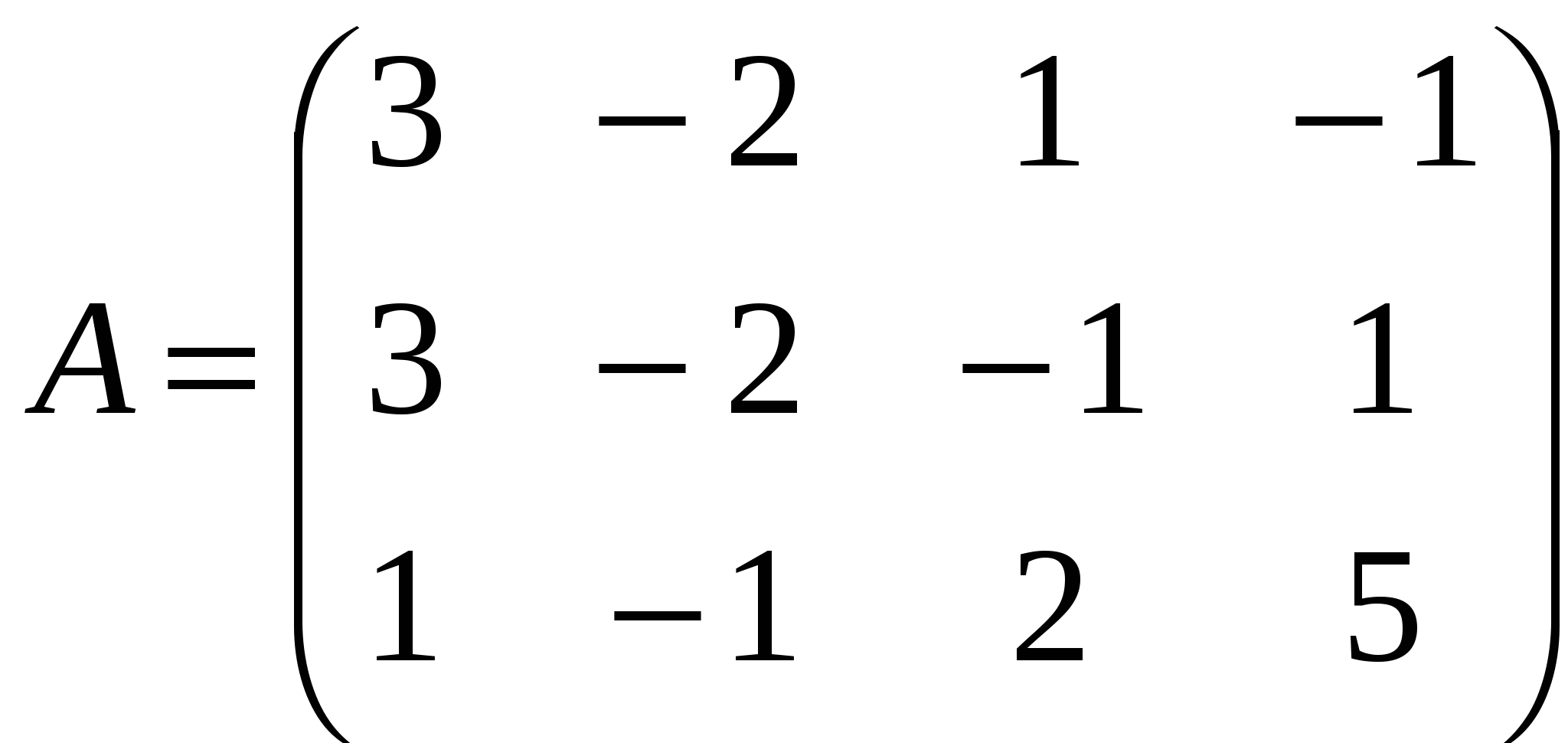 и и 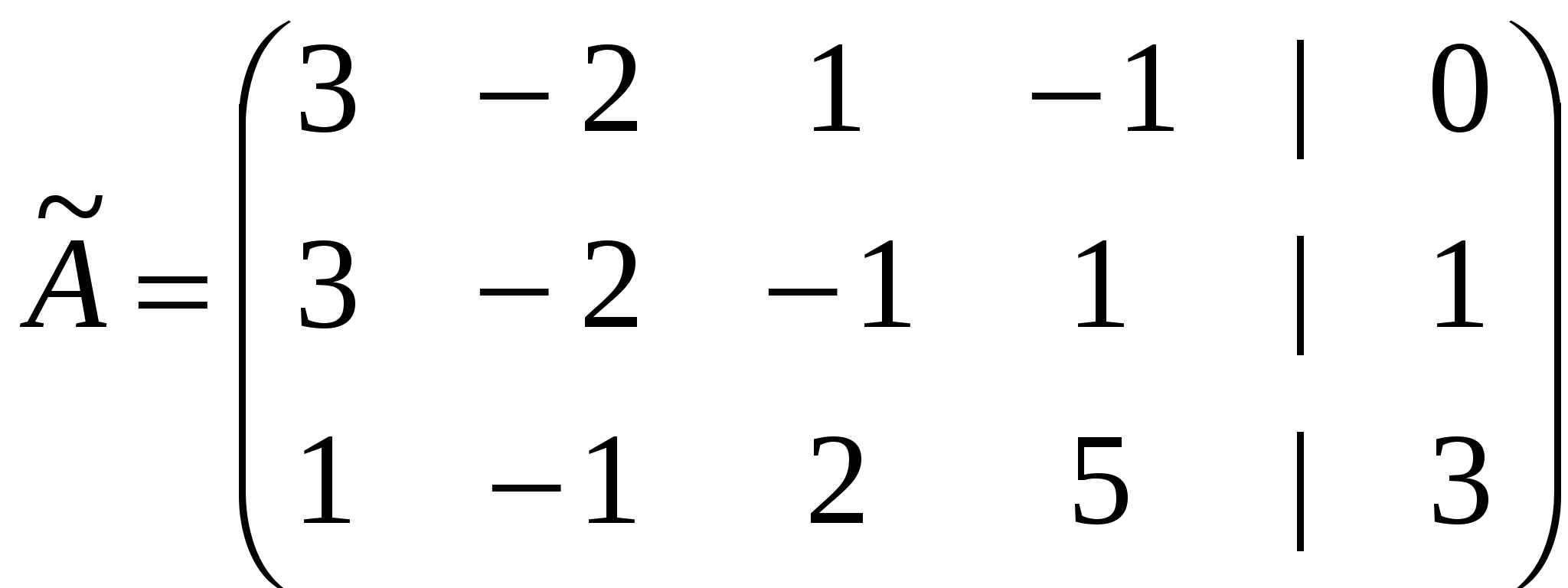 . .Если ранг основной матрицы равен рангу расширенной матрицы, то система совместна. Находим ранг основной матрицы: 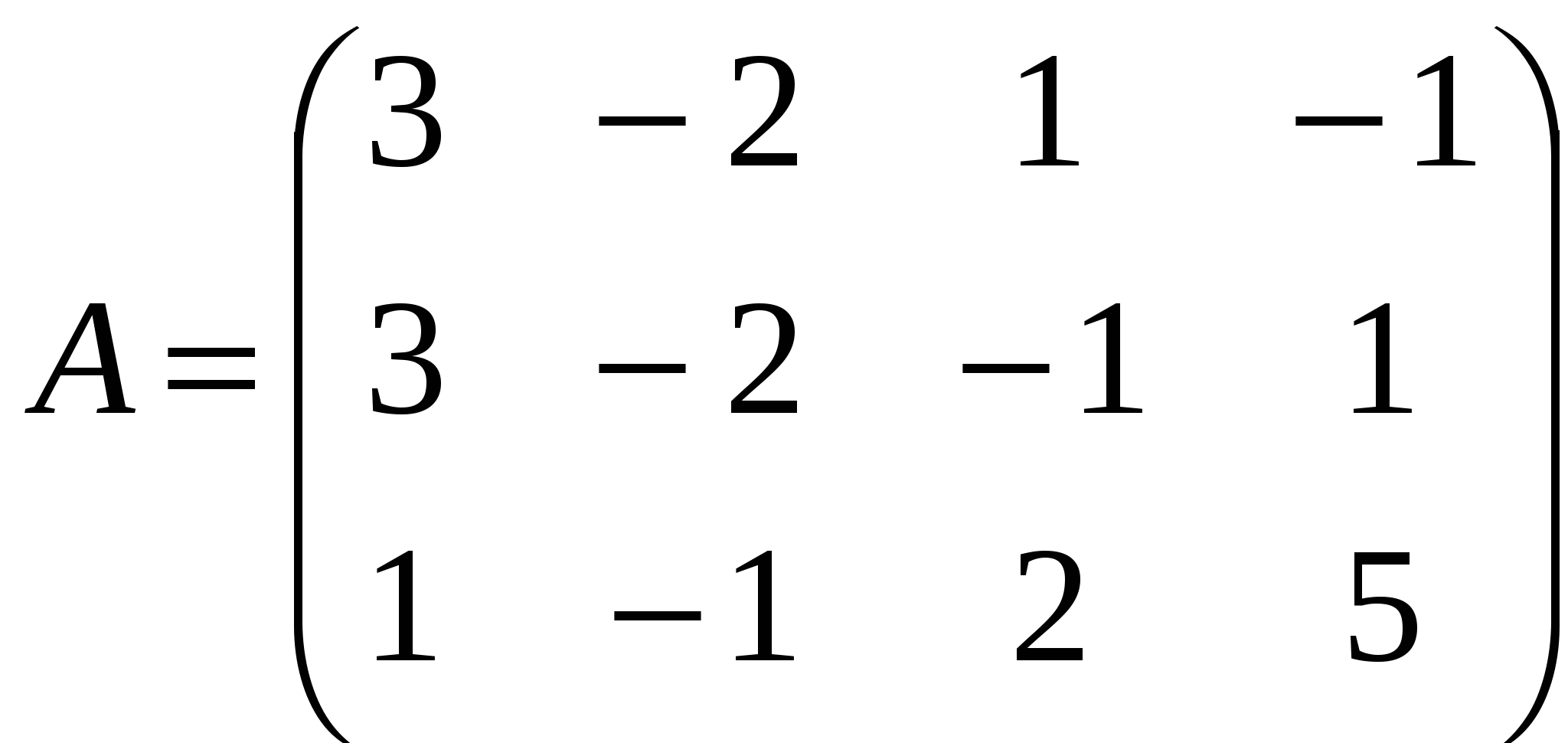 вторую строку вычтем с первой: вторую строку вычтем с первой: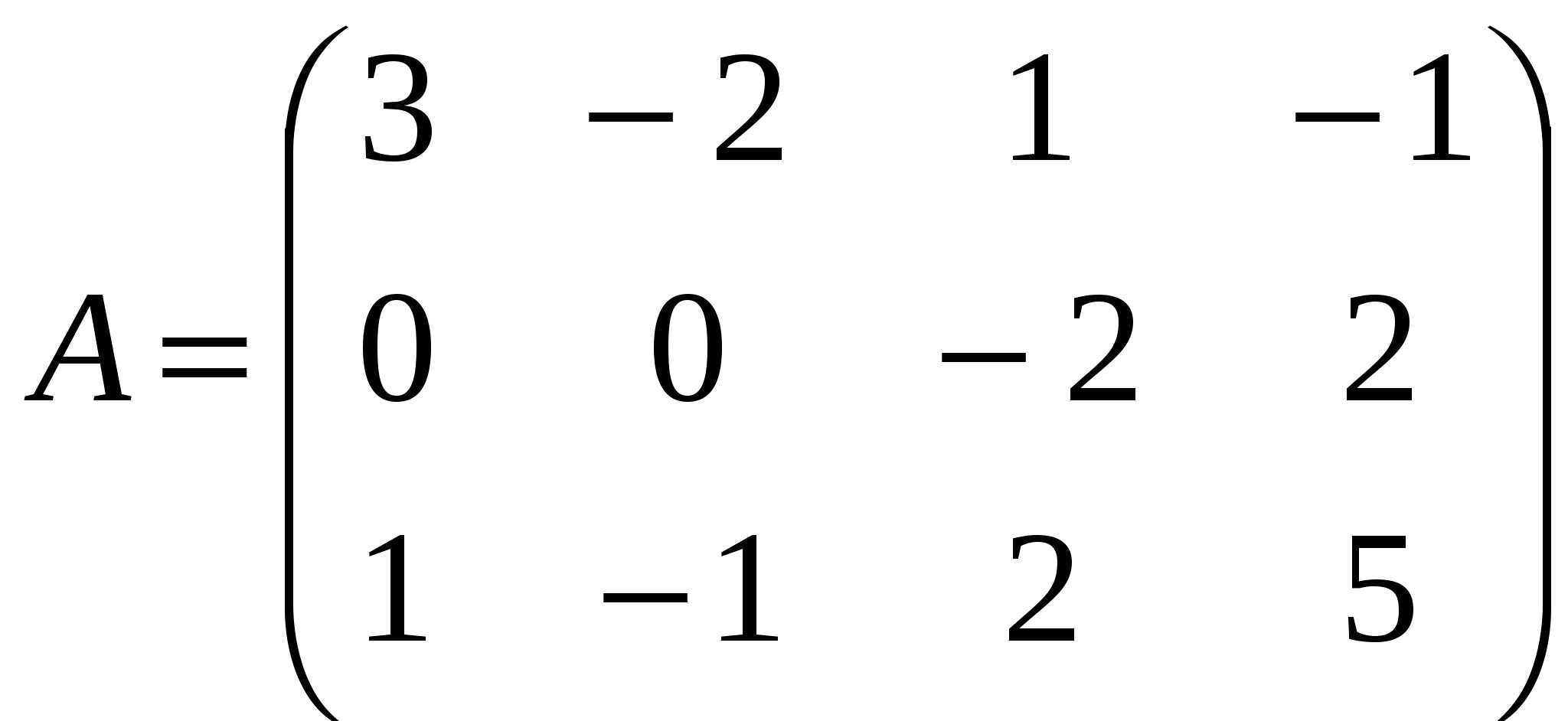 третью строку умножим на 3 и вычтем первую: третью строку умножим на 3 и вычтем первую: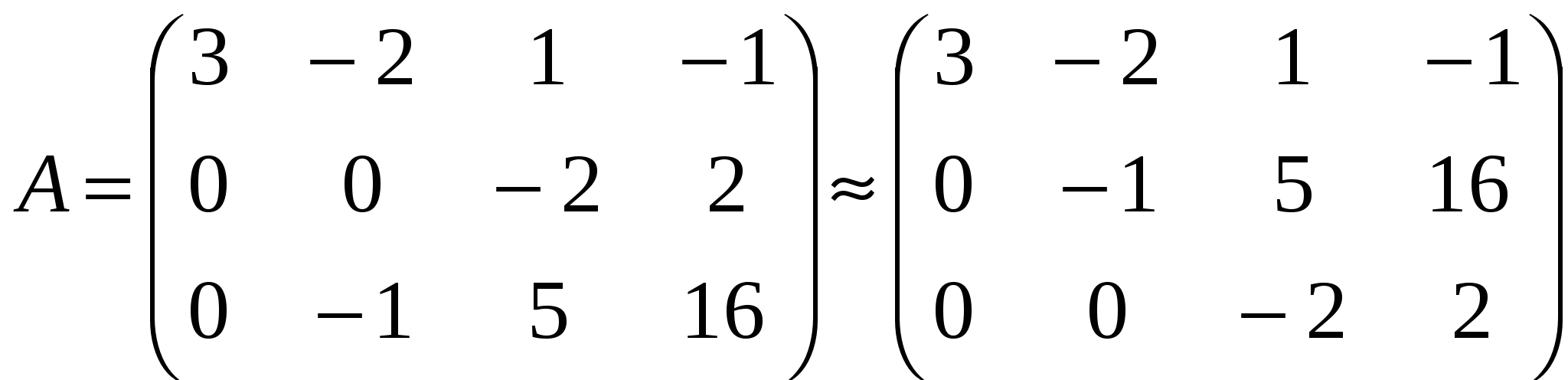 Количество ненулевых строк равно 3, следовательно, ранг основной матрицы равен 3. Следовательно, и ранг расширенной матрицы тоже равен 3. Таким образом по теореме Кронекера –Капелли система совместна. Так как ранг равен 3, а число неизвестных равно 4, то система уравнений имеет бесчисленное множество решений, т.е. система неопределенная. Задание №7 Решить систему линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса  Решение: 1) метод Гаусса Перепишем систему уравнений в матричном виде и решим его методом Гаусса 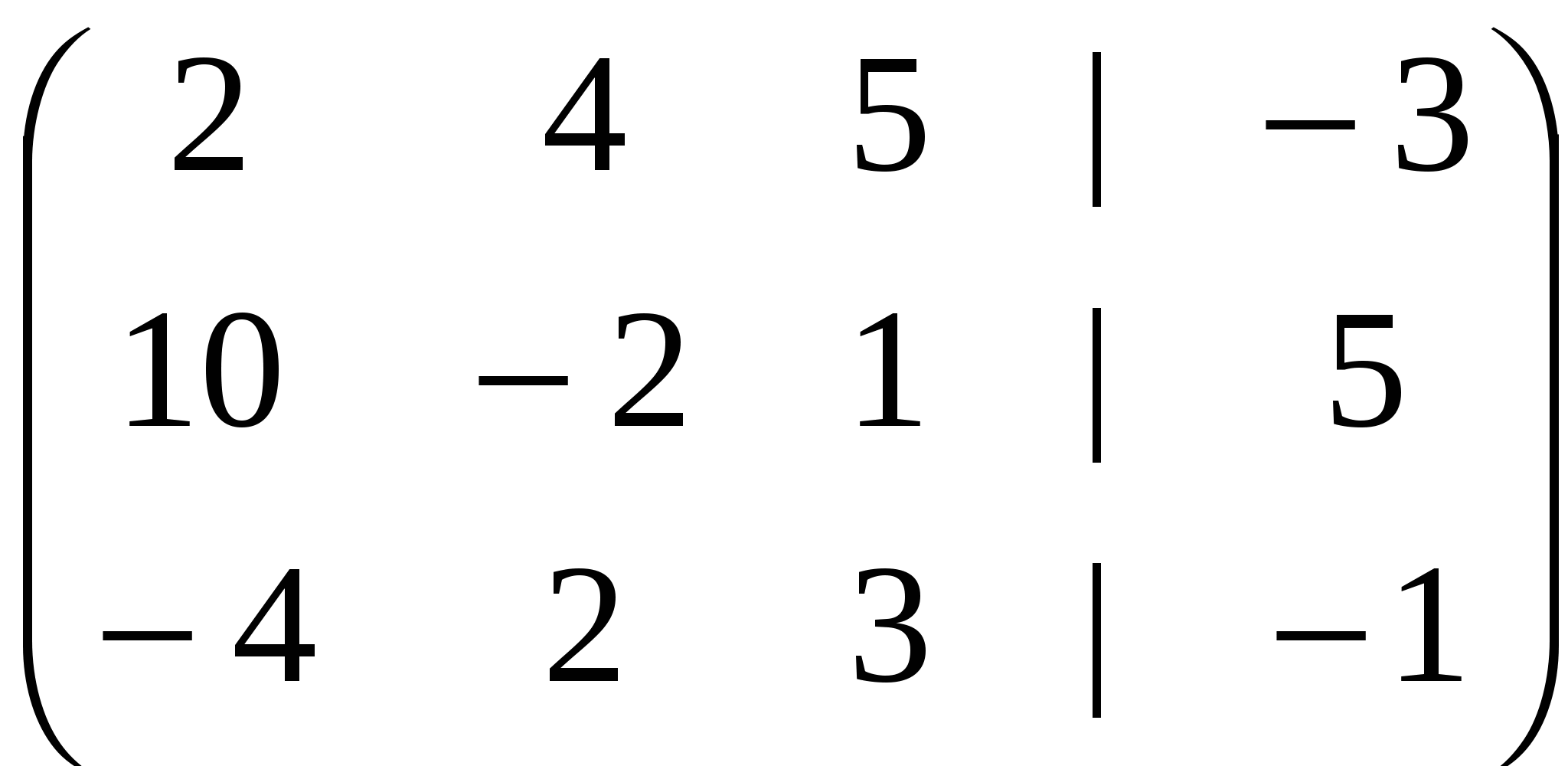 2-ую строку умножим на 0,2 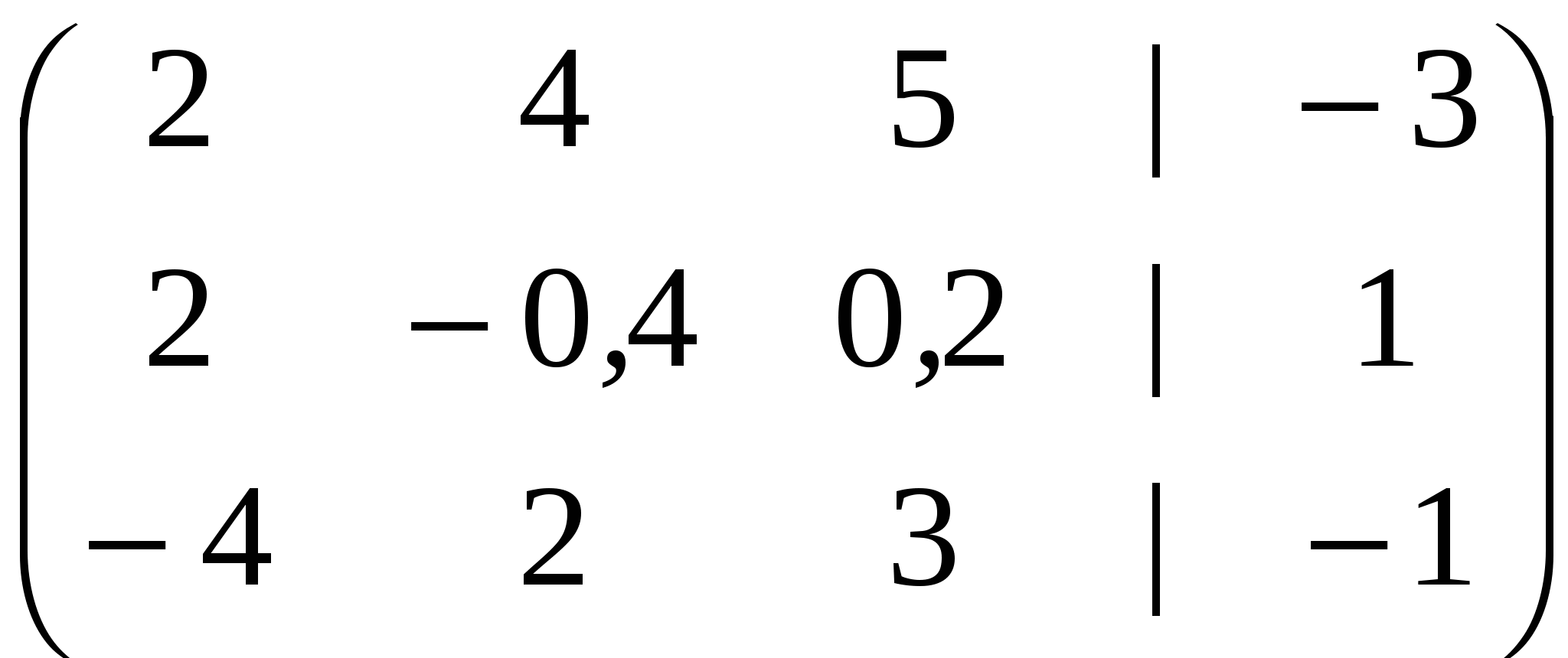 , вычтем первую строку , вычтем первую строку 3-ую строку умножаем на 0,5 и складываем 1-ую строку, получим: 3-ую строку умножаем на 0,5 и складываем 1-ую строку, получим:  ; 3-ую строку умножаем на 4,4 и складываем со 2-ой строкой, умноженную на 5 получим: ; 3-ую строку умножаем на 4,4 и складываем со 2-ой строкой, умноженную на 5 получим: 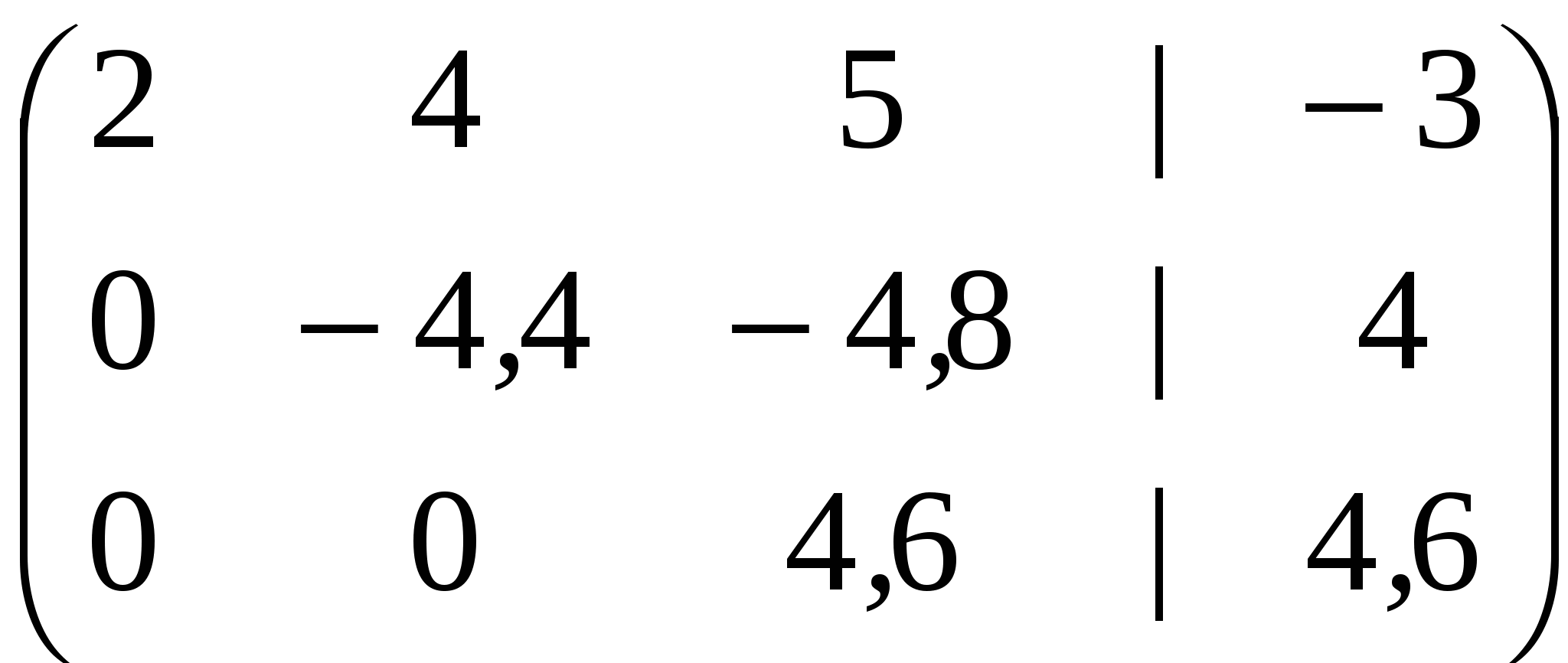 . Полученная матрица имеет треугольный вид. Отсюда . Полученная матрица имеет треугольный вид. Отсюда 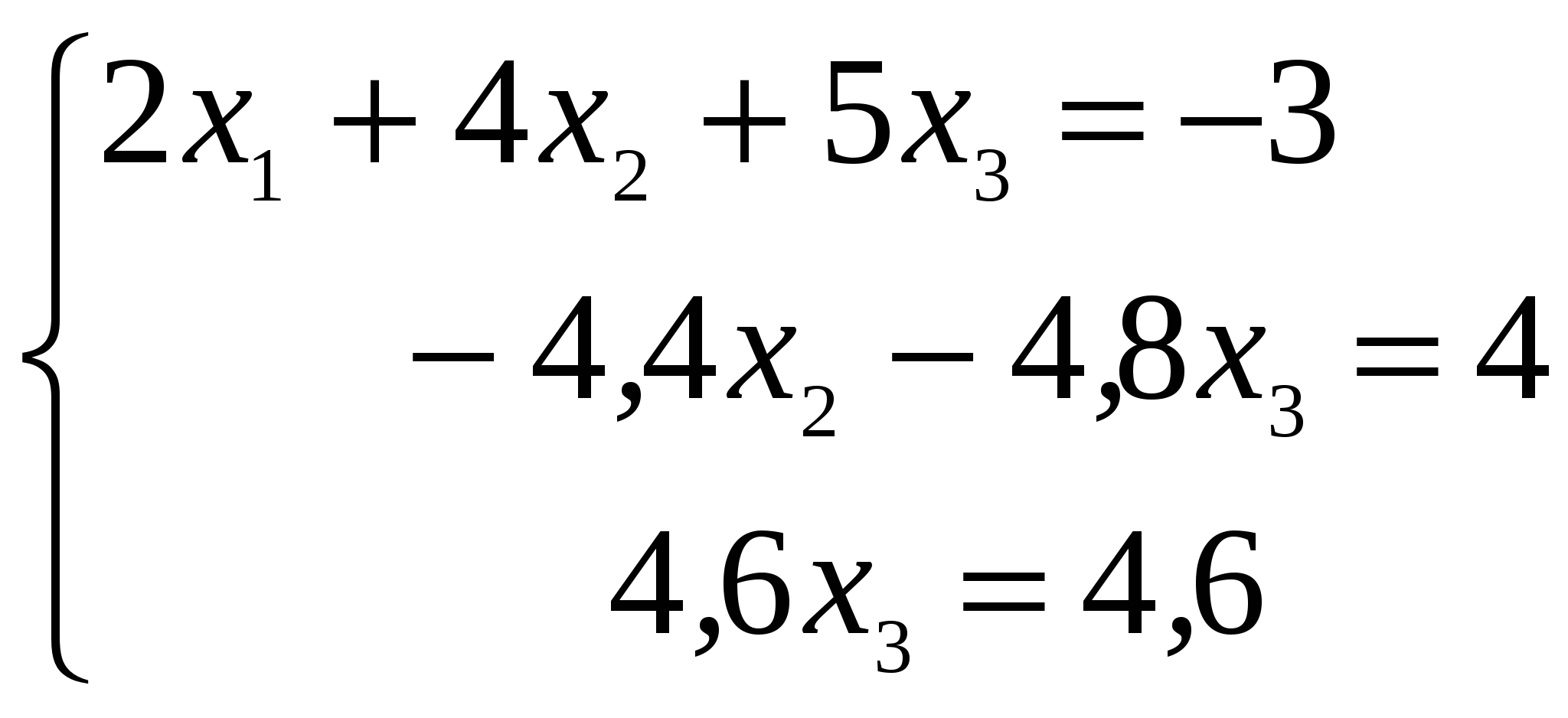 Следовательно, Следовательно,  отсюда отсюда 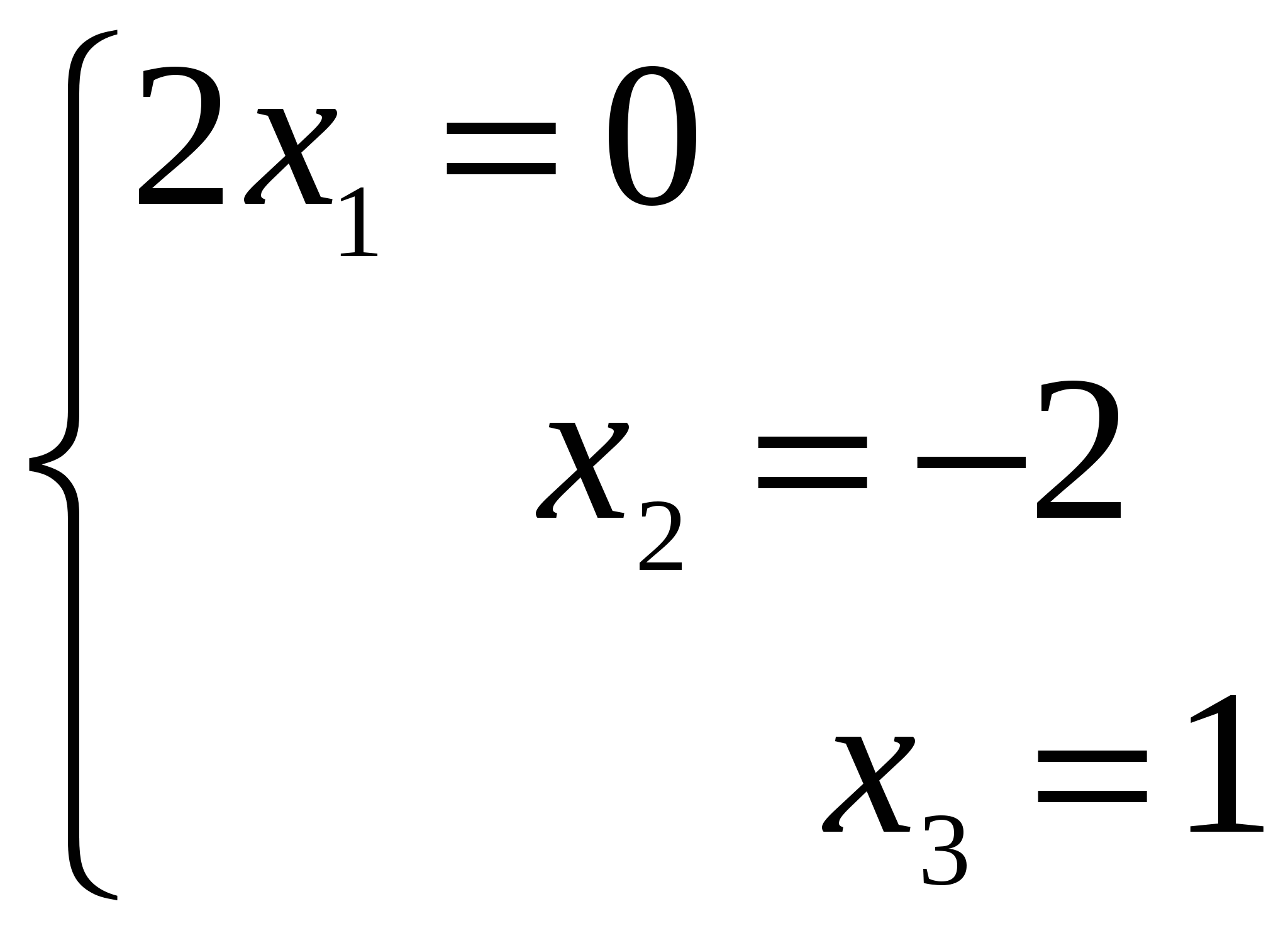 отсюда отсюда 2) средствами матричного исчисления Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:  Вектор B: BT=(-3,5,-1) Вектор B: BT=(-3,5,-1)С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B. Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е. Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1. Находим обратную матрицу матрицы А по формуле: 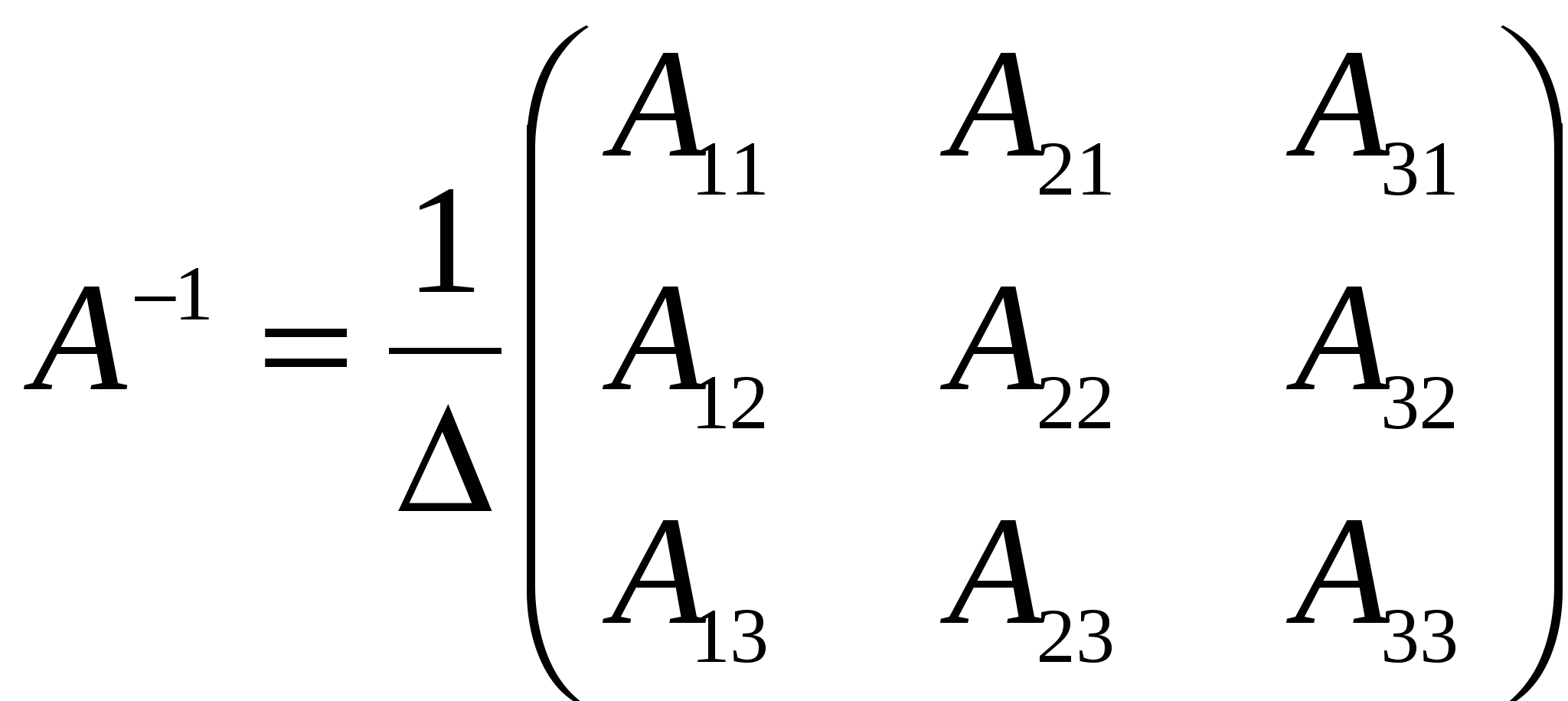 , , 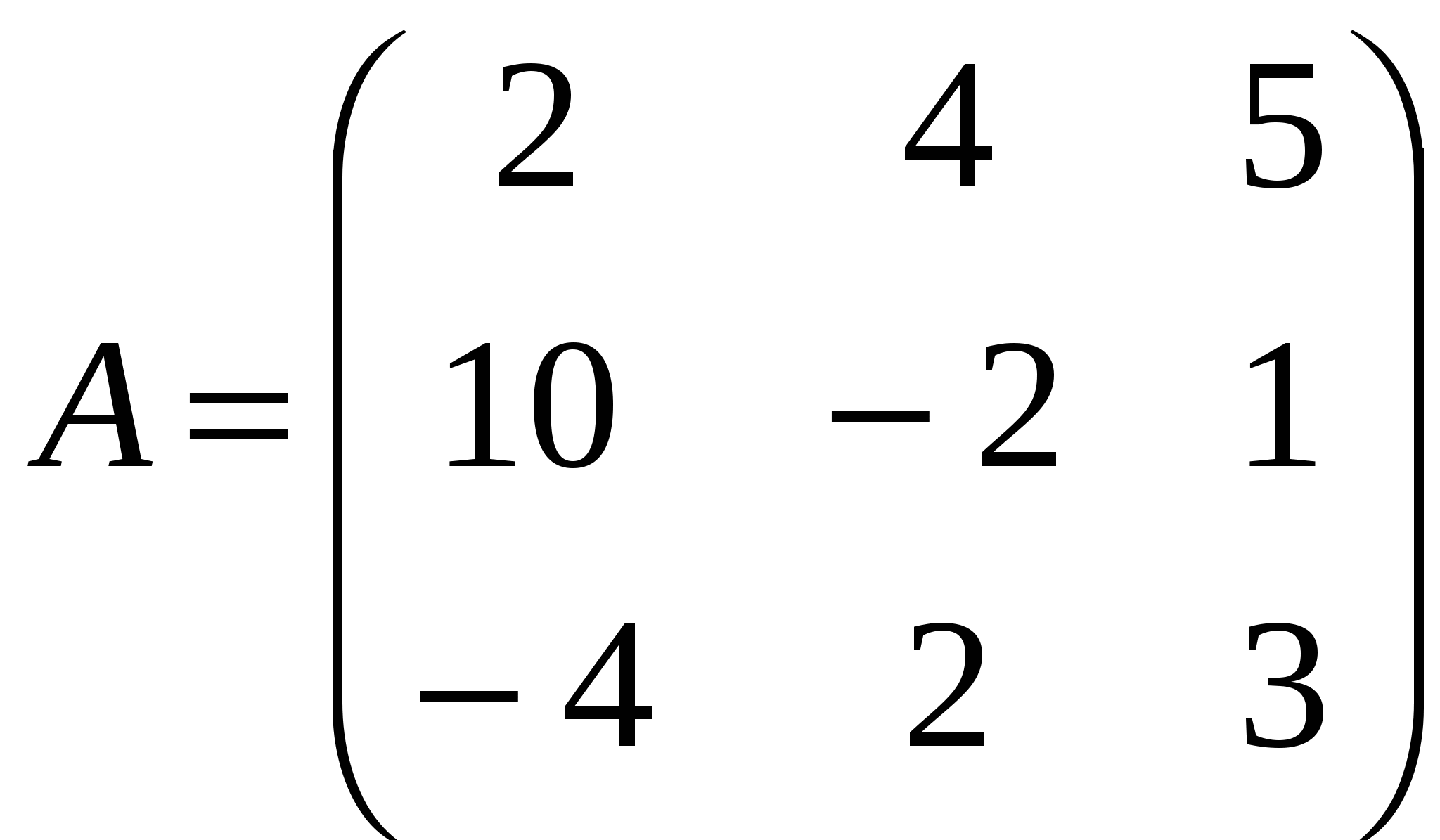 , , Отсюда 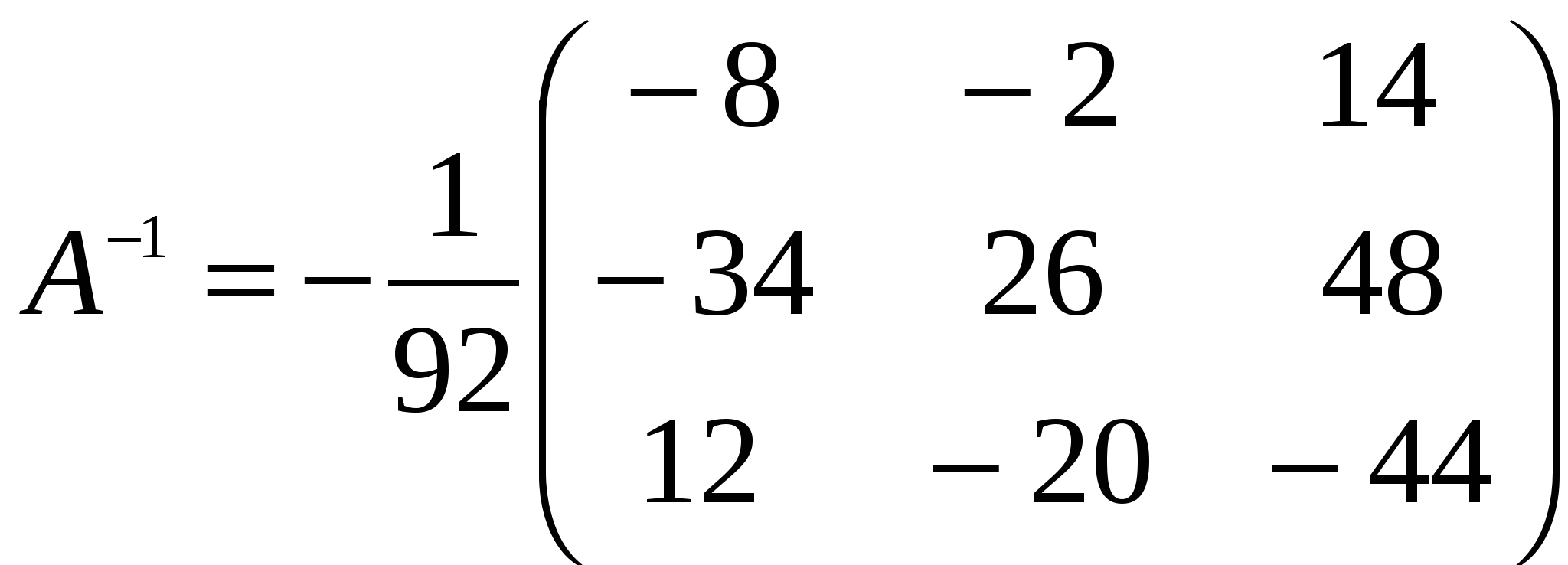 . Отсюда . Отсюда  , или , или 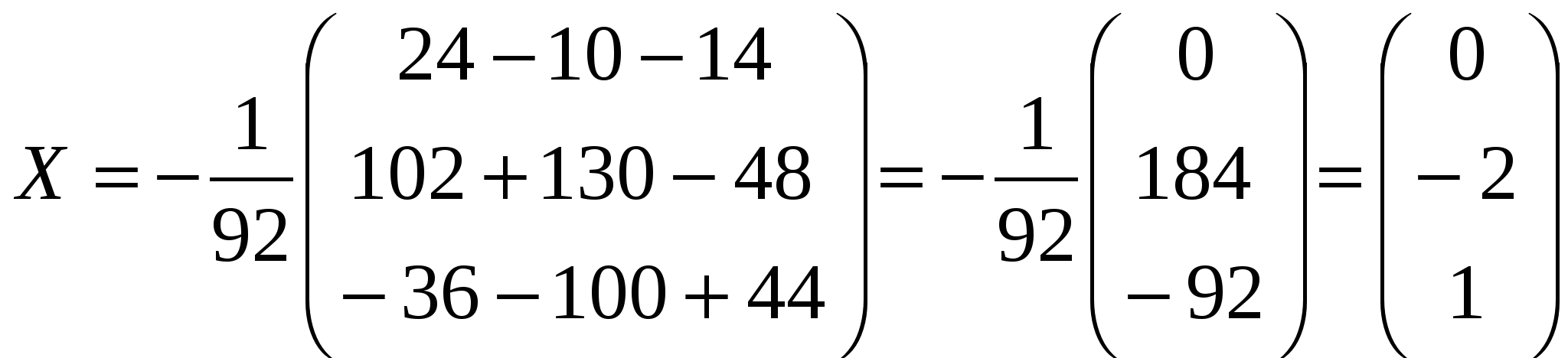 . Отсюда . Отсюда 3) по формулам Крамера Запишем систему в виде: 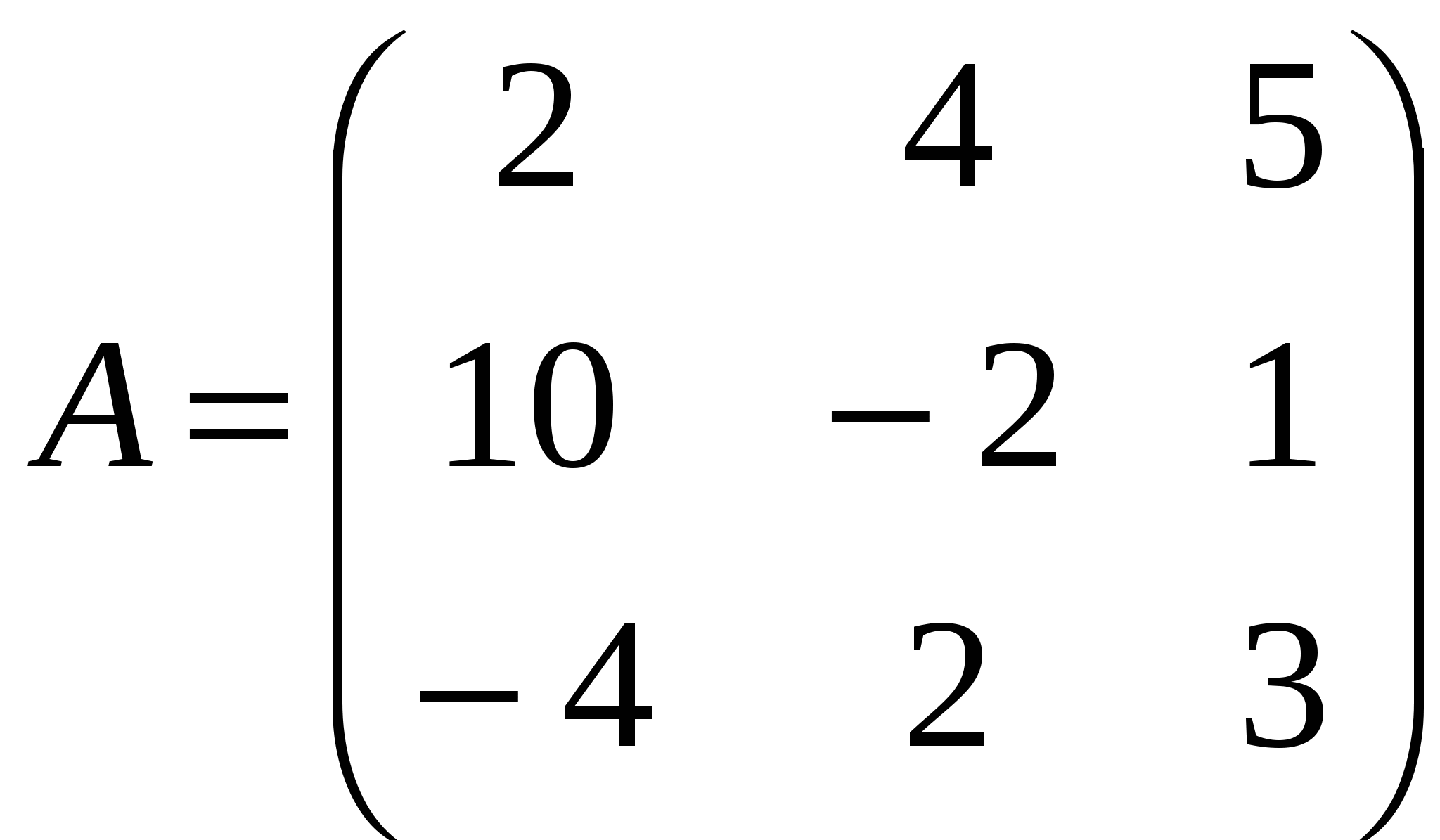 , , 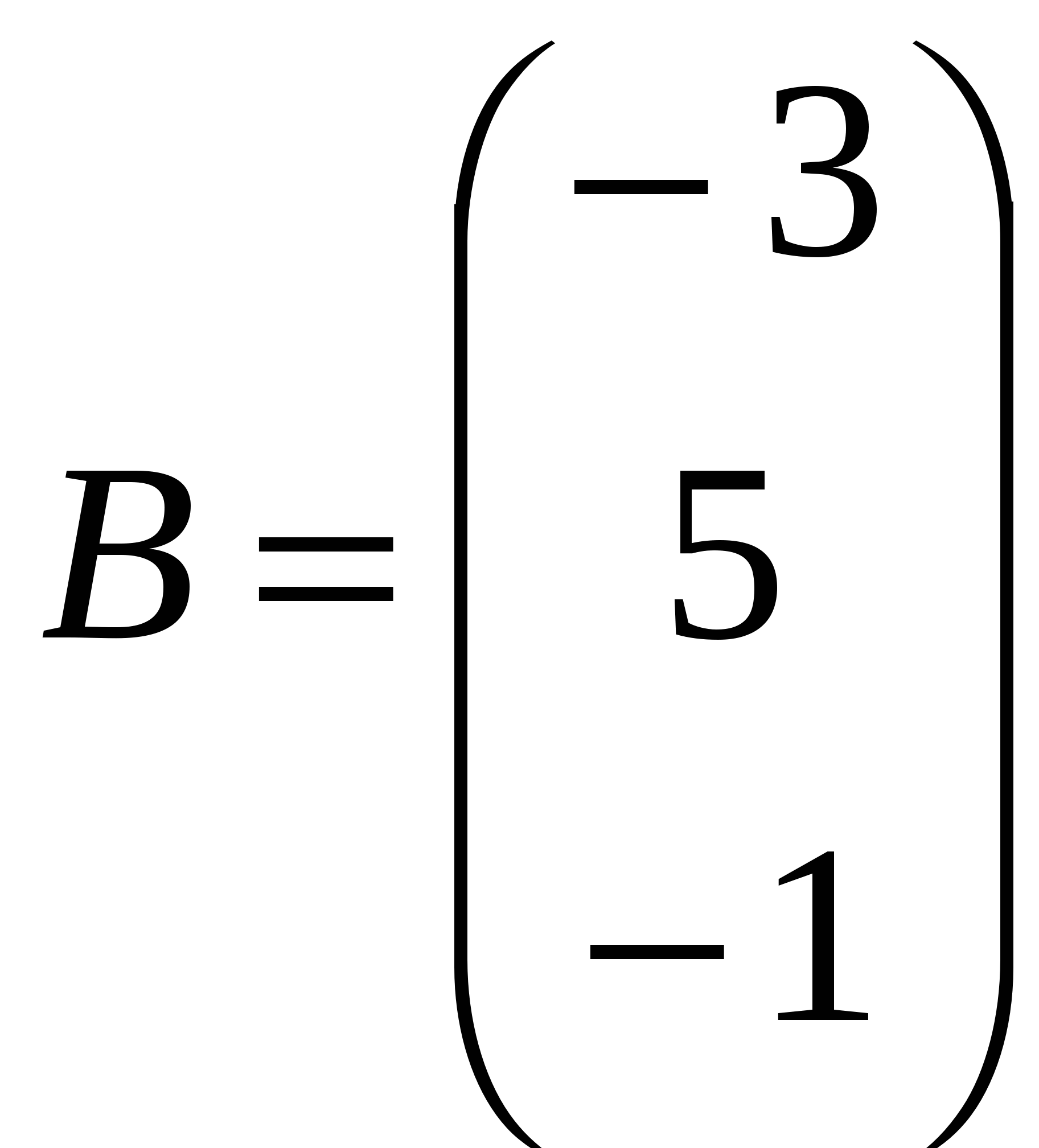  . Заменим первый столбец матрицы А, на вектор столбец В, получаем, . Заменим первый столбец матрицы А, на вектор столбец В, получаем, 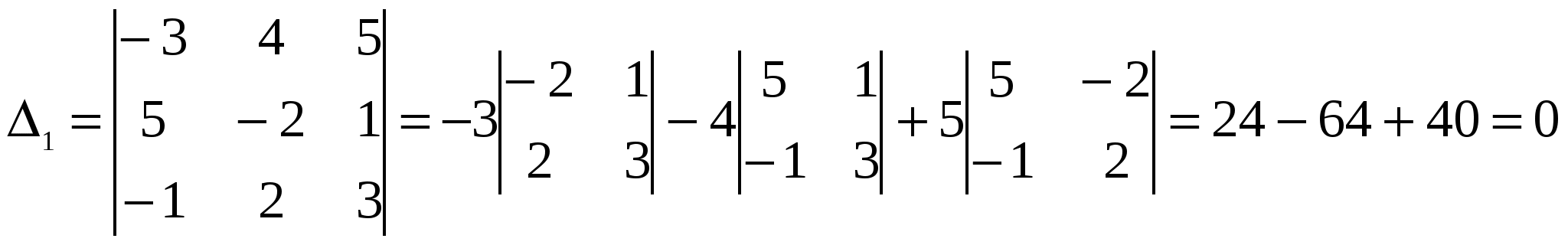 Заменим второй столбец матрицы А, на вектор столбец В, получаем, 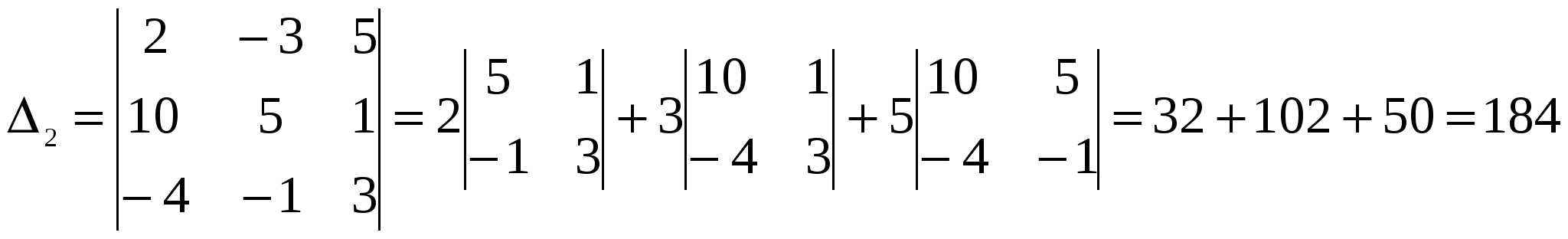 Заменим третий столбец матрицы А, на вектор столбец В, получаем, 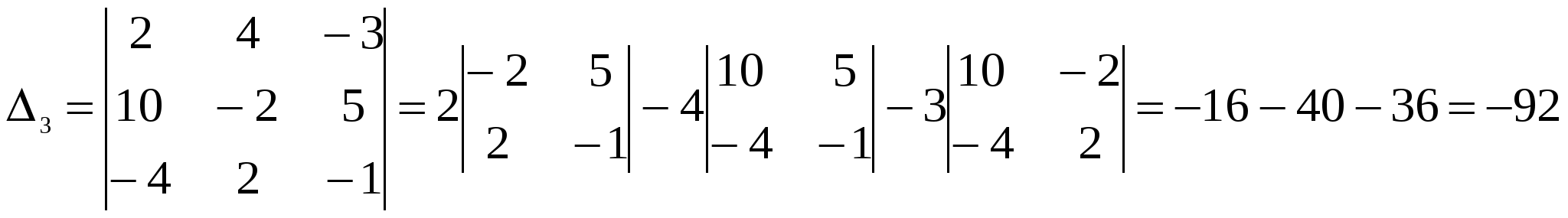 Ответ: Задание №8 Найти общее решение данной системы линейных алгебраических уравнений методом Гаусса.уравнений 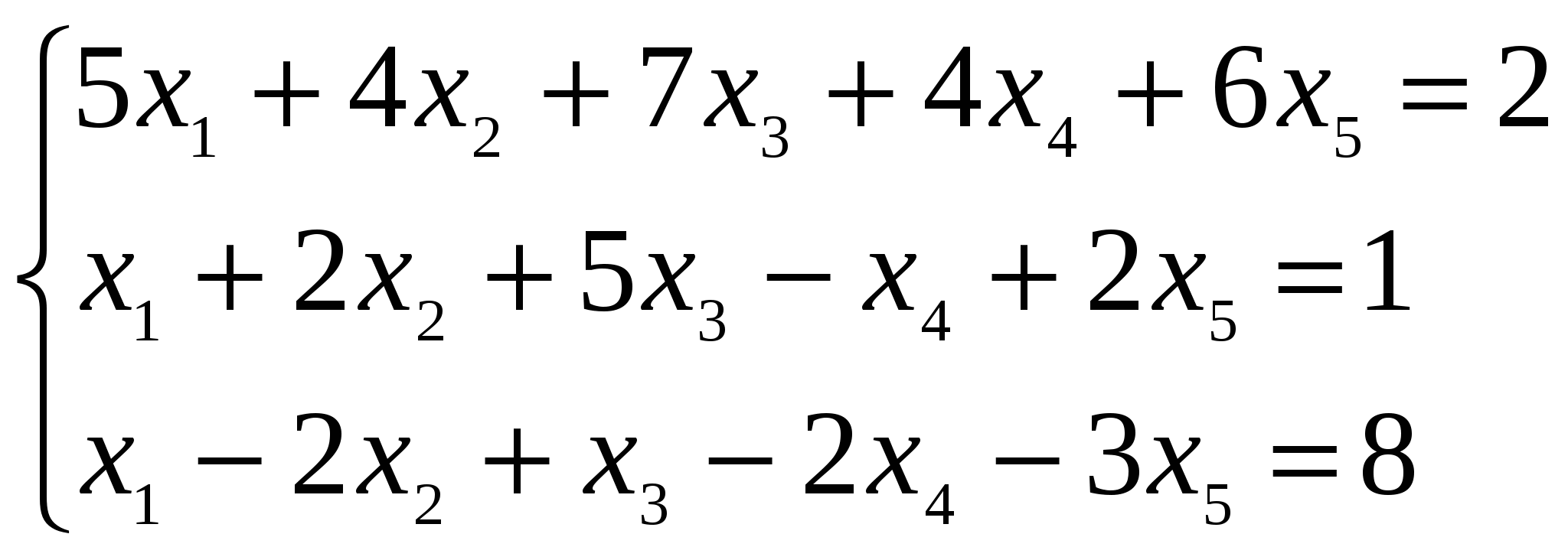 Решение: Расширенная матрица:  Вторую строку умножим на 5 и вычтем первую: 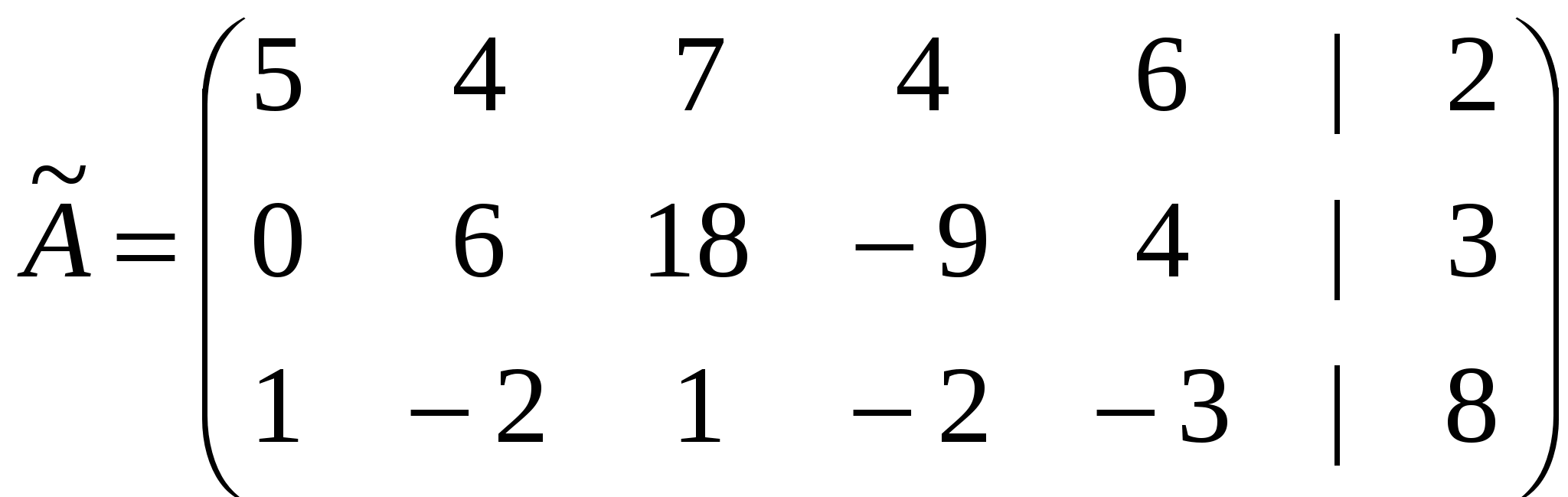 Третью строку умножим на 5 и вычтем первую: Третью строку умножим на 5 и вычтем первую: . Умножим третью строку на 3 и сложим со второй строкой умноженную на 7 . Умножим третью строку на 3 и сложим со второй строкой умноженную на 7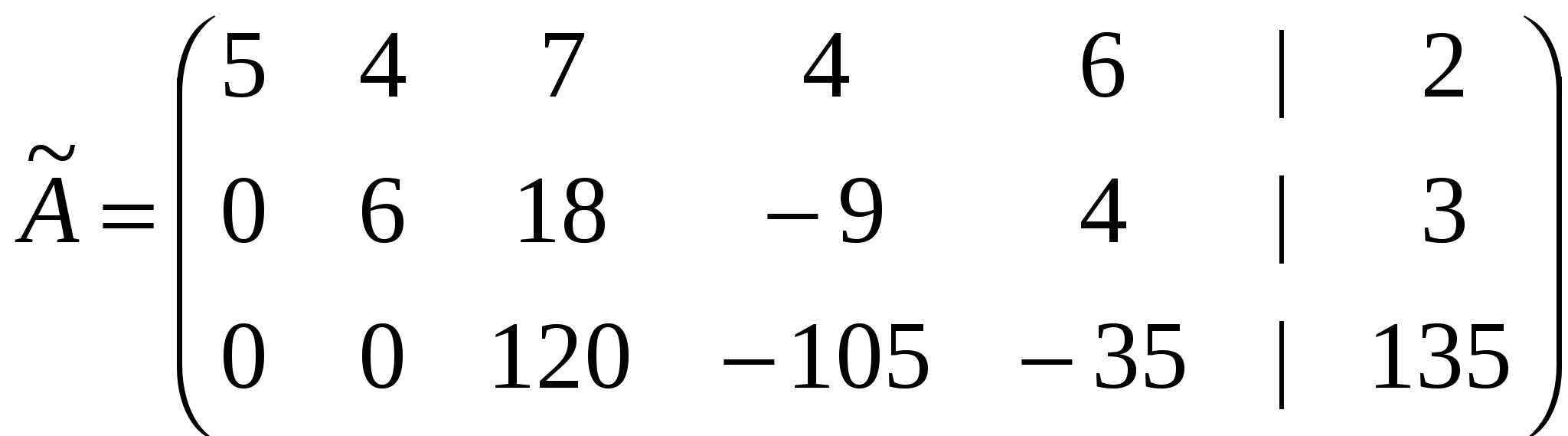 Первую строку делим на5, вторую на 6, третью на 120, получим: Первую строку делим на5, вторую на 6, третью на 120, получим: Таким образом:  После преобразований системы получим общее решение уравнения: 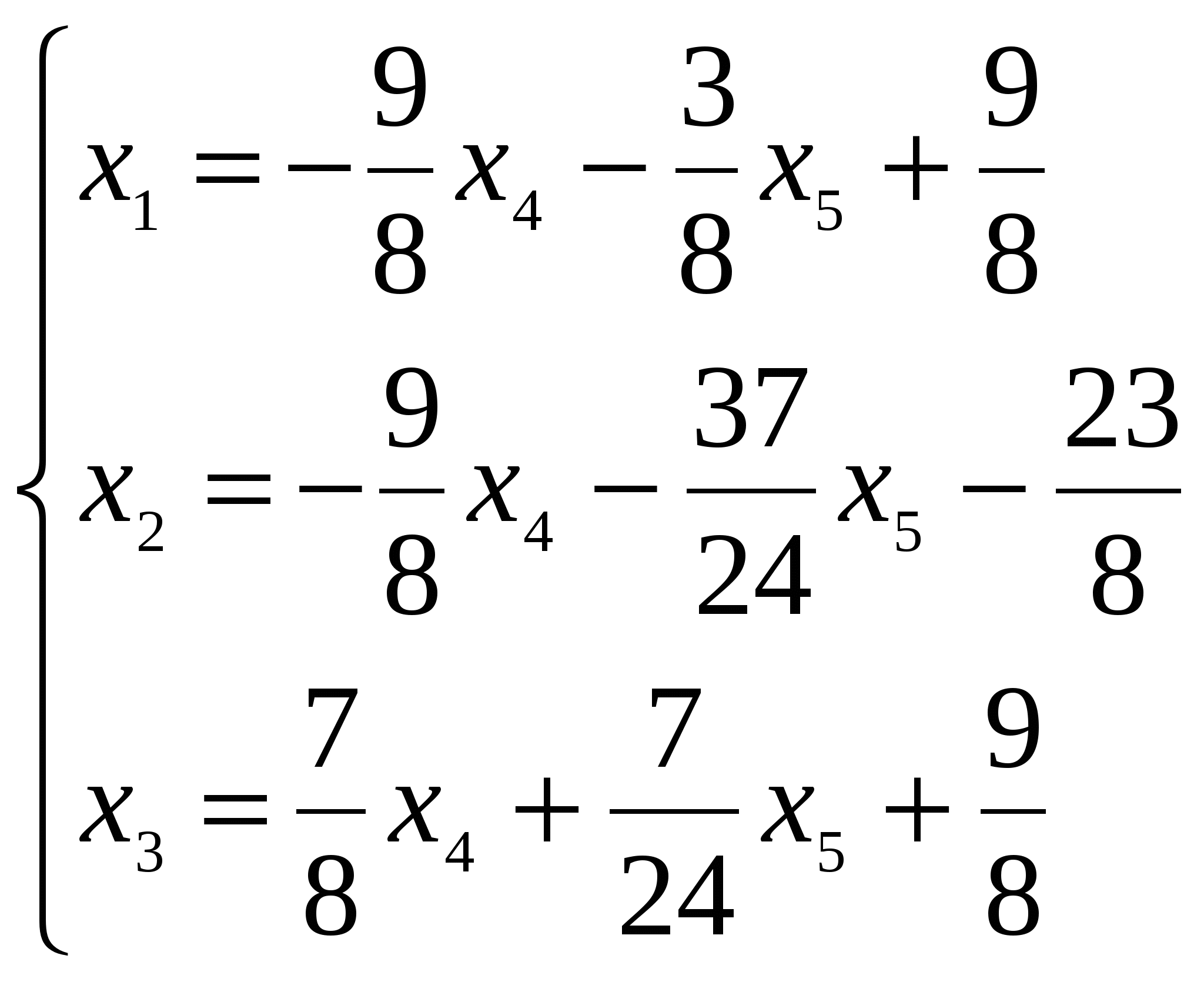 Задание №9 Задание №3 Показать, что векторы Решение: Итак, даны векторы а1(5;0;-2), а2(3;1;1), а3(-4;1;0), а4(32;1;-3). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора а в этом базисе. Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор а нельзя разложить по данному базису. Вычислим определитель матрицы:  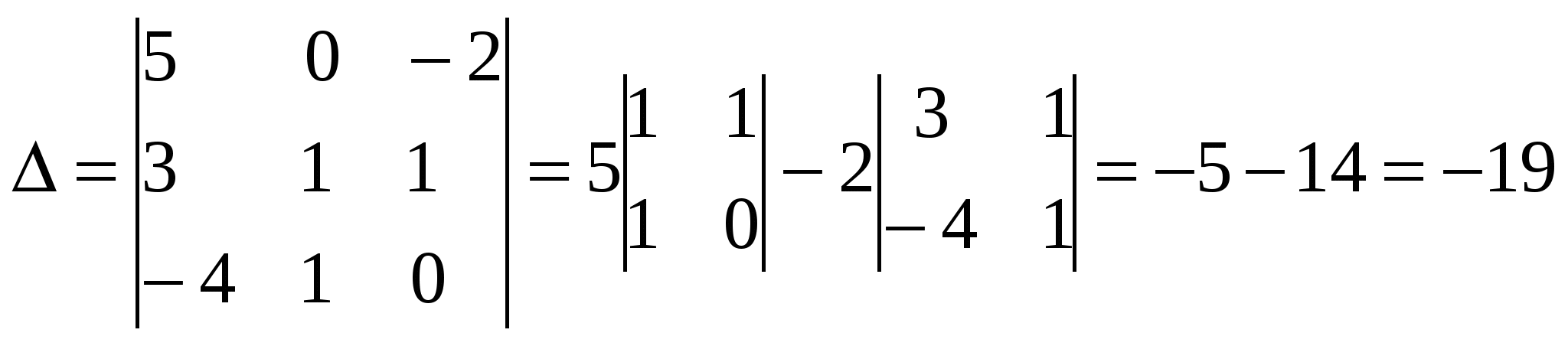 Определитель матрицы равен ∆ =-19 Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор а можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство: а = α1а1 + α2а2 + α3а3 Запишем данное равенство в координатной форме: (32;1;-3) = α(5;0;-2) + α(3;1;1) + α(-4;1;0) Используя свойства векторов, получим следующее равенство: (32;1;-3) = (5α1;0α1;-2α1;) + (3α2;α2;α2;) + (-4α3;α3;0α3;) (32;1;-3) = (5α1 +3α2 -4α3;α2 +α3;-2α1 +α2 ) По свойству равенства векторов имеем: 5α1 +3α2 -4α3 =32 α2 + α3 = 1 -2α1 +α2 =-3 Решаем полученную систему уравнений методом Гаусса или по формулам Крамера получим Ответ: 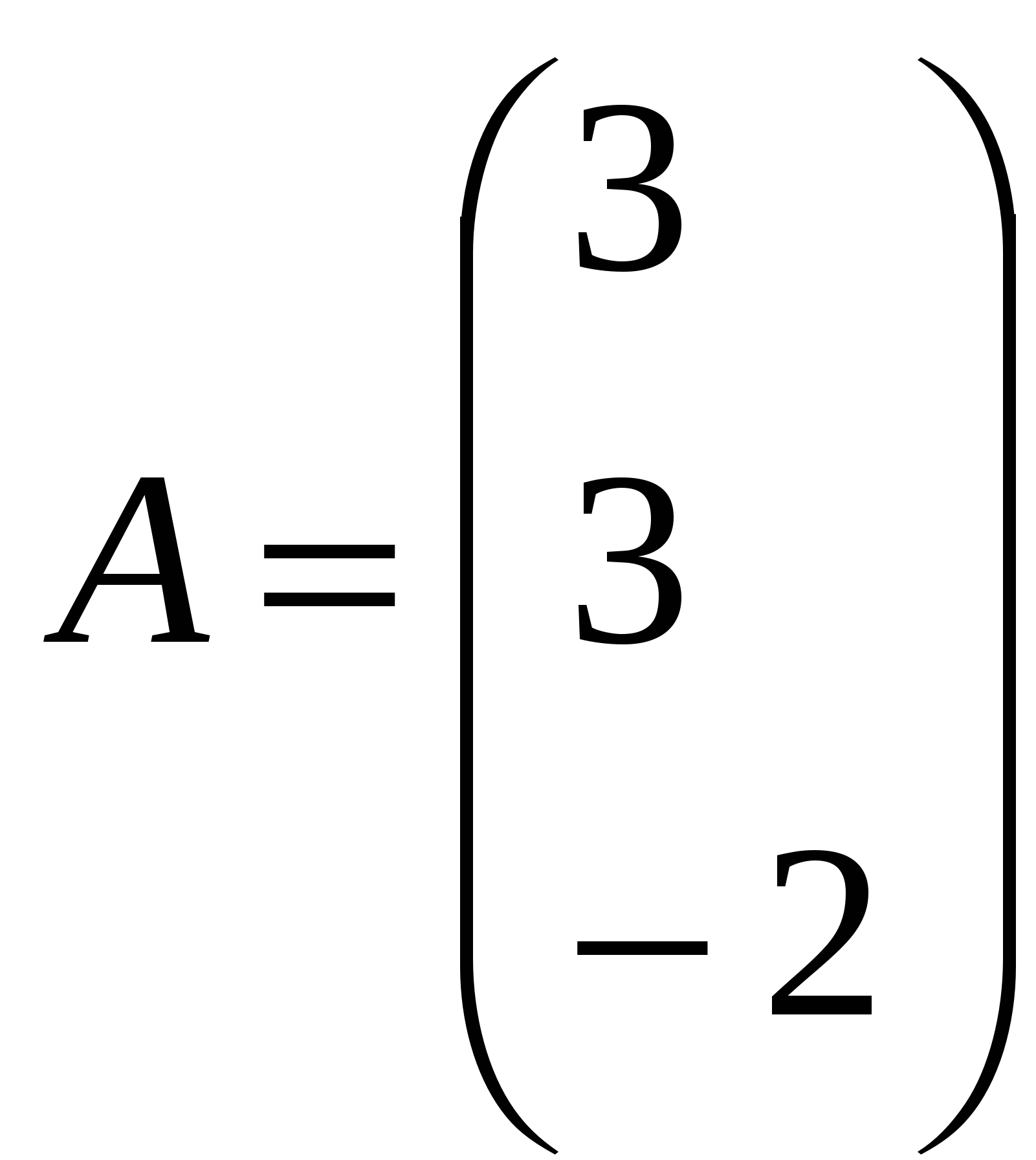 , а = 3а1 +3а2 -2а3 , а = 3а1 +3а2 -2а3 Задание №4 Задание №5 Привести систему к системе с базисом методом Жордана - Гаусса и найти одно базисное решение. 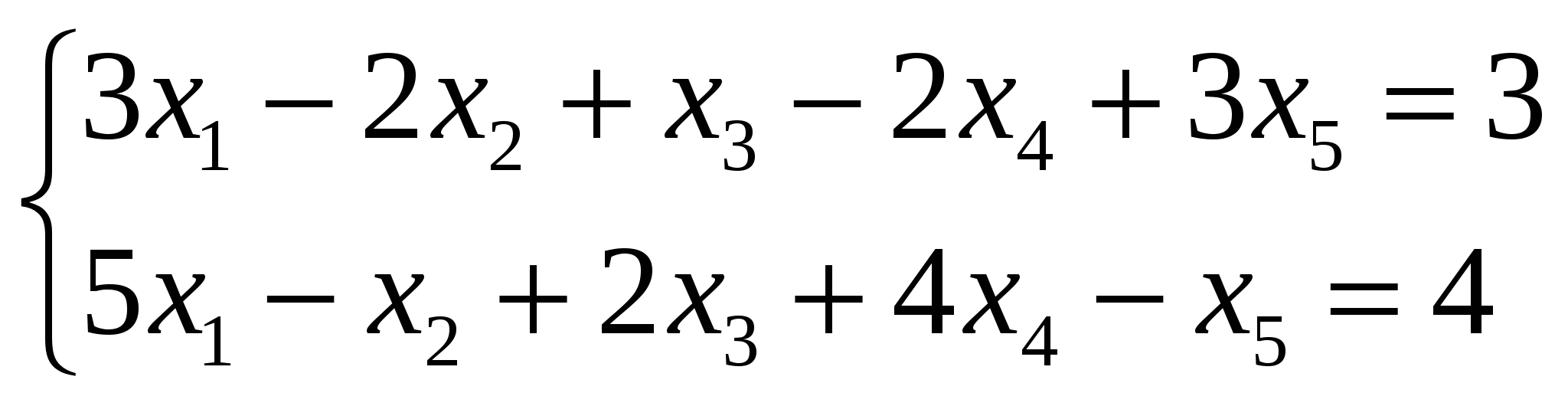 Решение Запишем систему в виде таблицы:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы. Разрешающий элемент равен (3). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ РЭ - разрешающий элемент (3), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
или
Разрешающий элемент равен 7/3 На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. Представим расчет каждого элемента в виде таблицы:
или
Теперь исходную систему можно записать как: 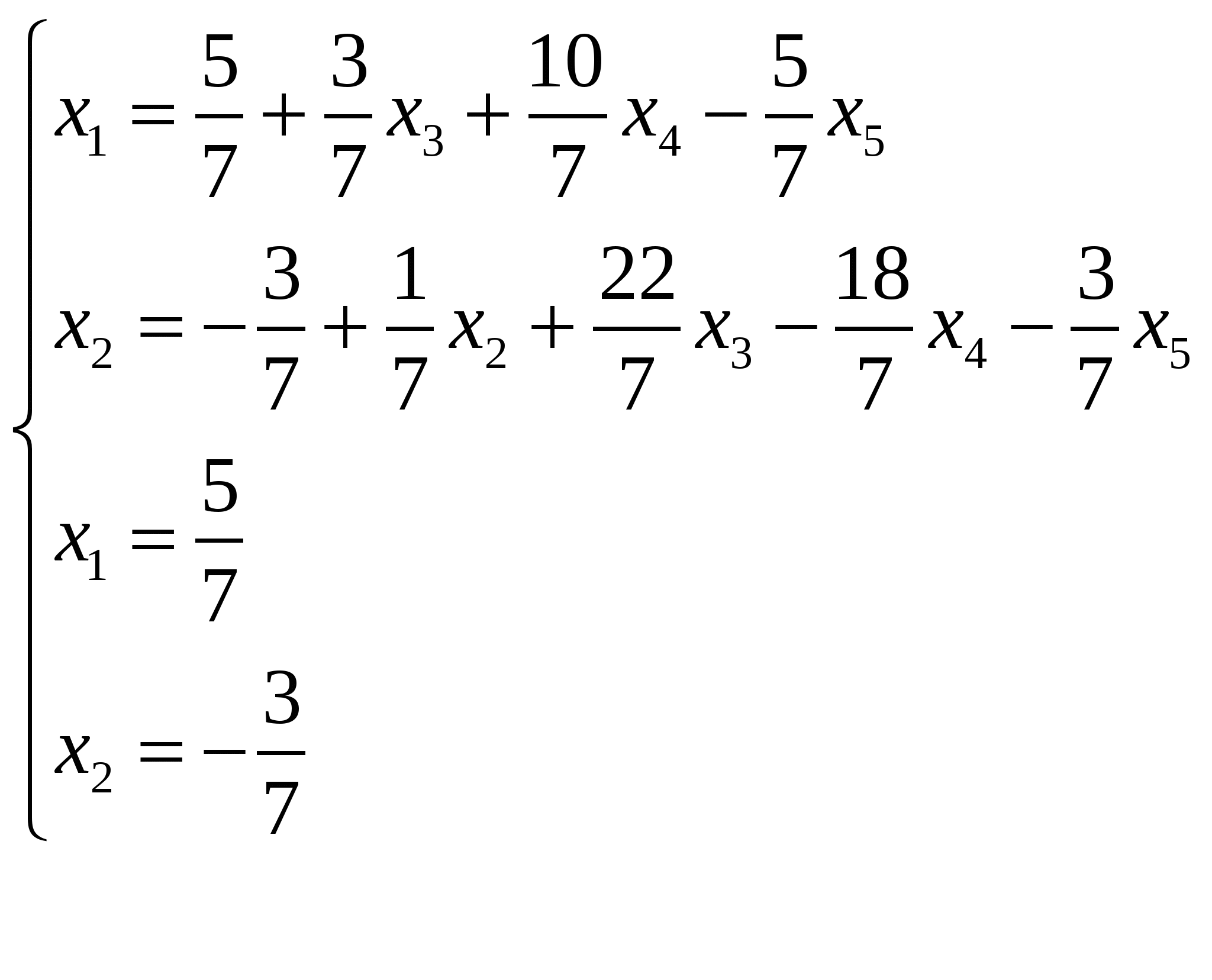 Необходимо переменные x3,x4,x5 принять в качестве свободных переменных и через них выразить остальные переменные. Приравняем переменные x3,x4,x5 к 0 , получим: Ответ: Задание №6 Найти два опорных решения канонической системы уравнений: 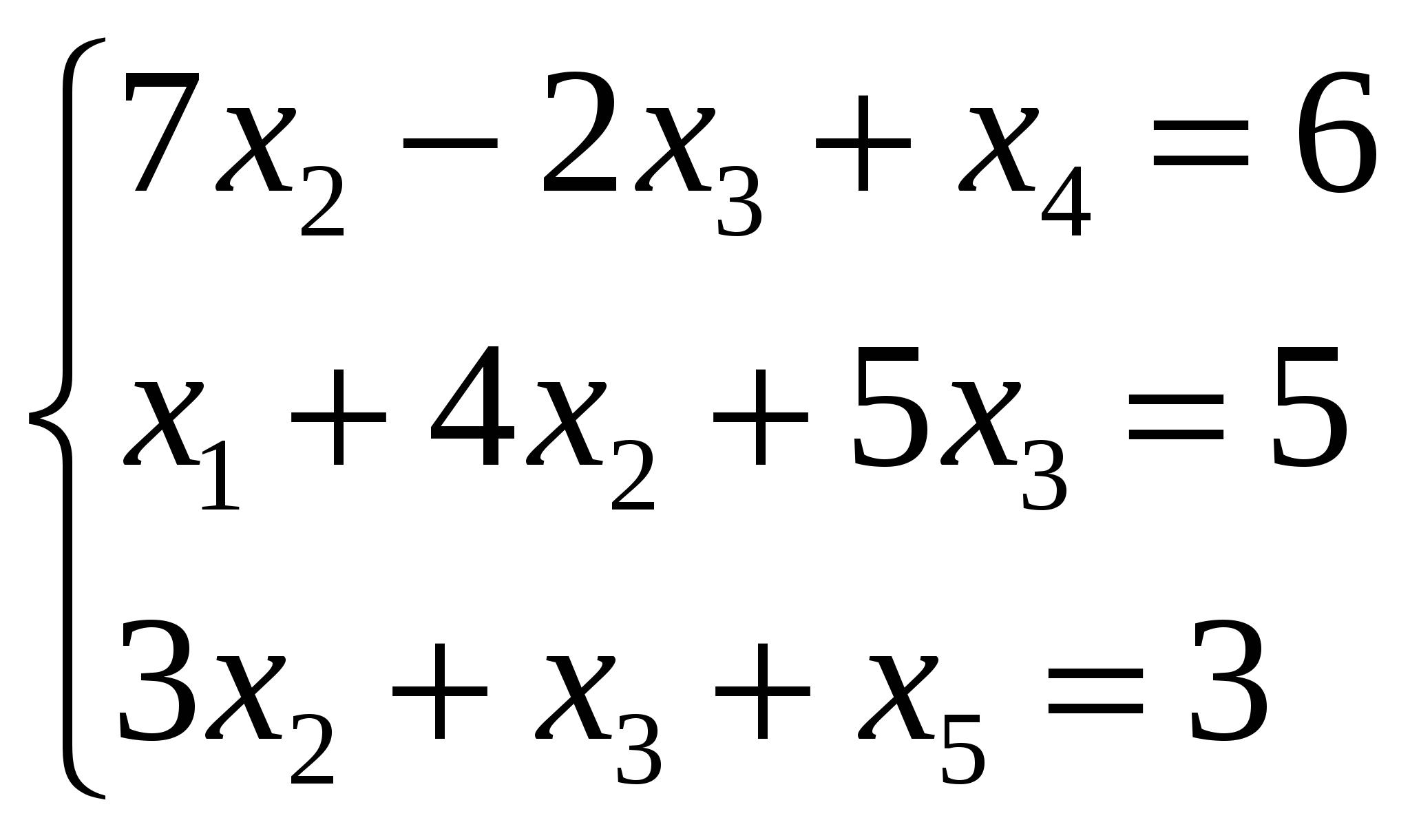 Решение: Данная система является системой с базисом относительно переменных Так как при свободных неизвестных имеются положительные коэффициенты, то возможен переход к эквивалентной канонической системе. Переход осуществим согласно алгоритму преобразования однократного замещения. Составляем таблицу
Таблица заполнена по виду системы, с учетом замены 1 и 2 строк. Базисные переменные записаны в левом столбце таблицы в том порядке, в котором они присутствуют в уравнениях исходной системы. За разрешающий столбец взяли столбец из коэффициентов под свободной переменной Преобразуем заполненную таблицу. В новой таблице свободная переменная В результате пересчета получим таблицу
Составляем ещё одну таблицу
В результате мы получаем систему: 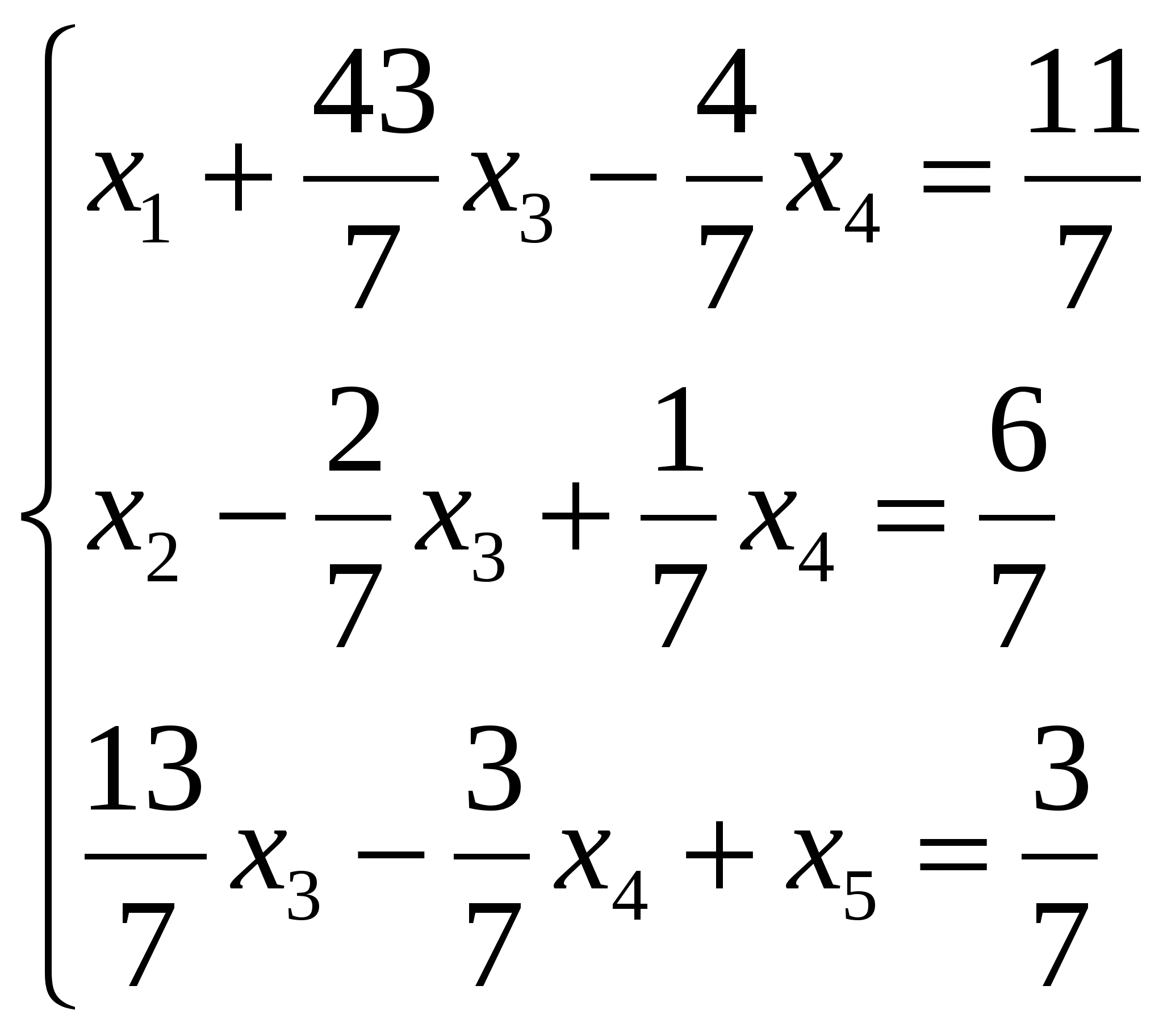 . Полагая, что . Полагая, что Ответ: Задание №7 Найти собственные значения и собственные векторы данной матрицы 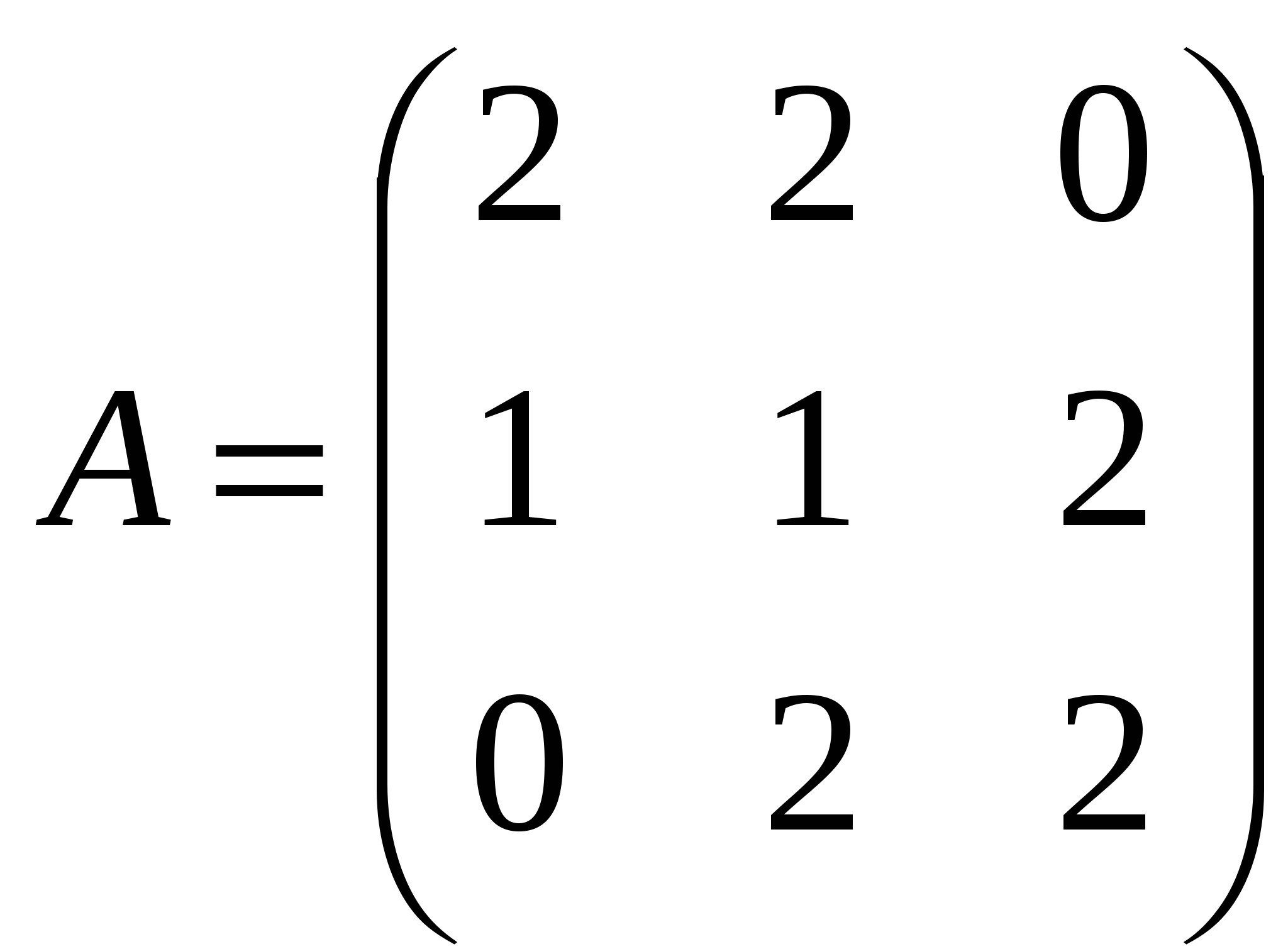 Решение: Составляем систему для определения координат собственных векторов: (2 - λ)x1 + 2x2 + 0x3 = 0 x1 + (1 - λ)x2 + 2x3 = 0 0x1 + 2x2 + (2 - λ)x3 = 0 Составляем характеристическое уравнение и решаем его. 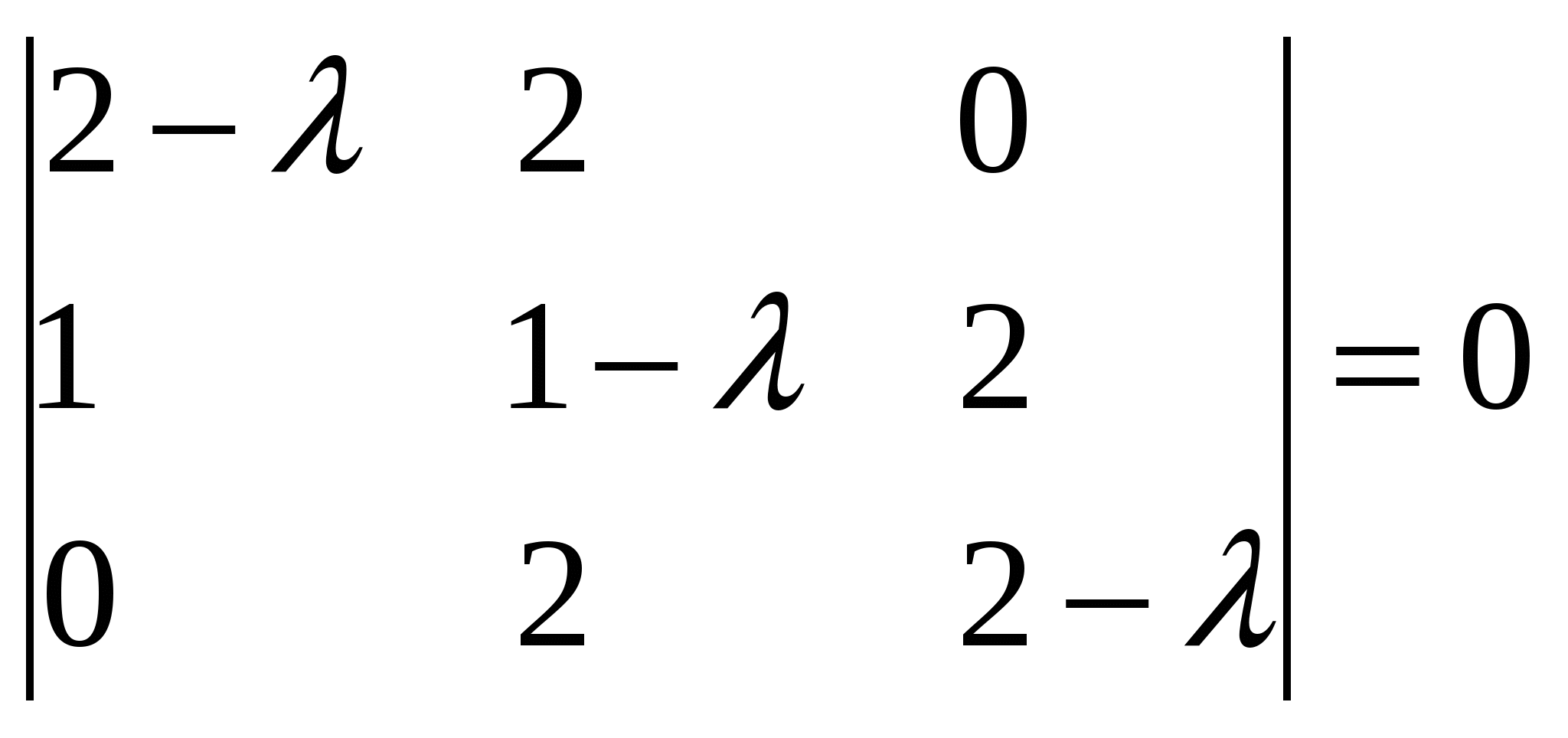 Для этого находим определитель матрицы и приравниваем полученное выражение к нулю. 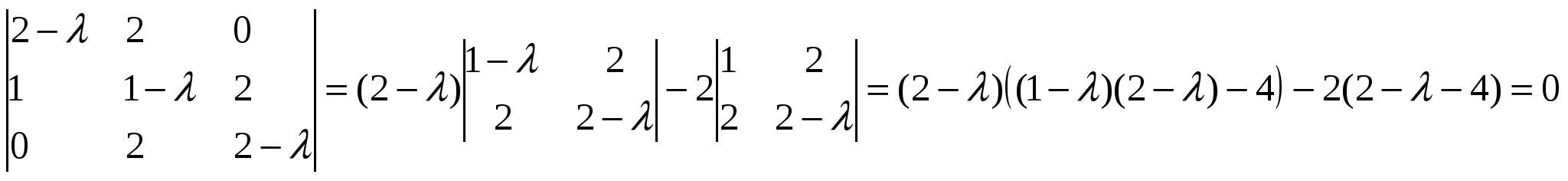 После преобразований, получаем: λ3 - 5λ2 +2λ +8 = 0 Один из корней уравнения равен λ1 = -1 Тогда характеристическое уравнение можно записать как (λ +1)( λ2 -6λ + 8)=0. λ2 -6 λ+8 = 0 Для собственного числа λ1 =-1 находим собственный вектор: Составляем систему для определения координат собственных векторов: Подставляя λ = -1 в систему, имеем: 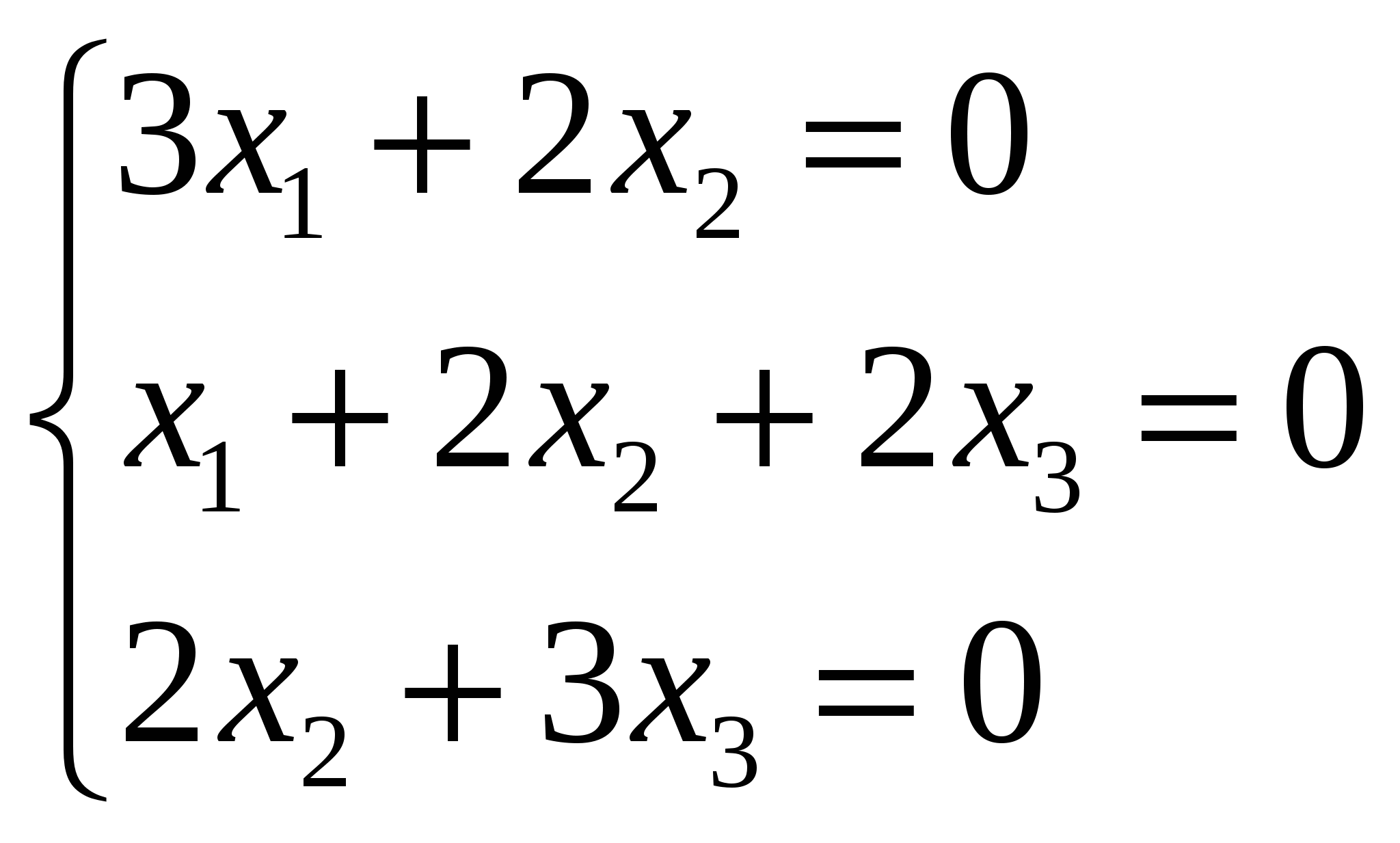 Пусть x1 - свободное неизвестное, тогда выразим через него все остальные 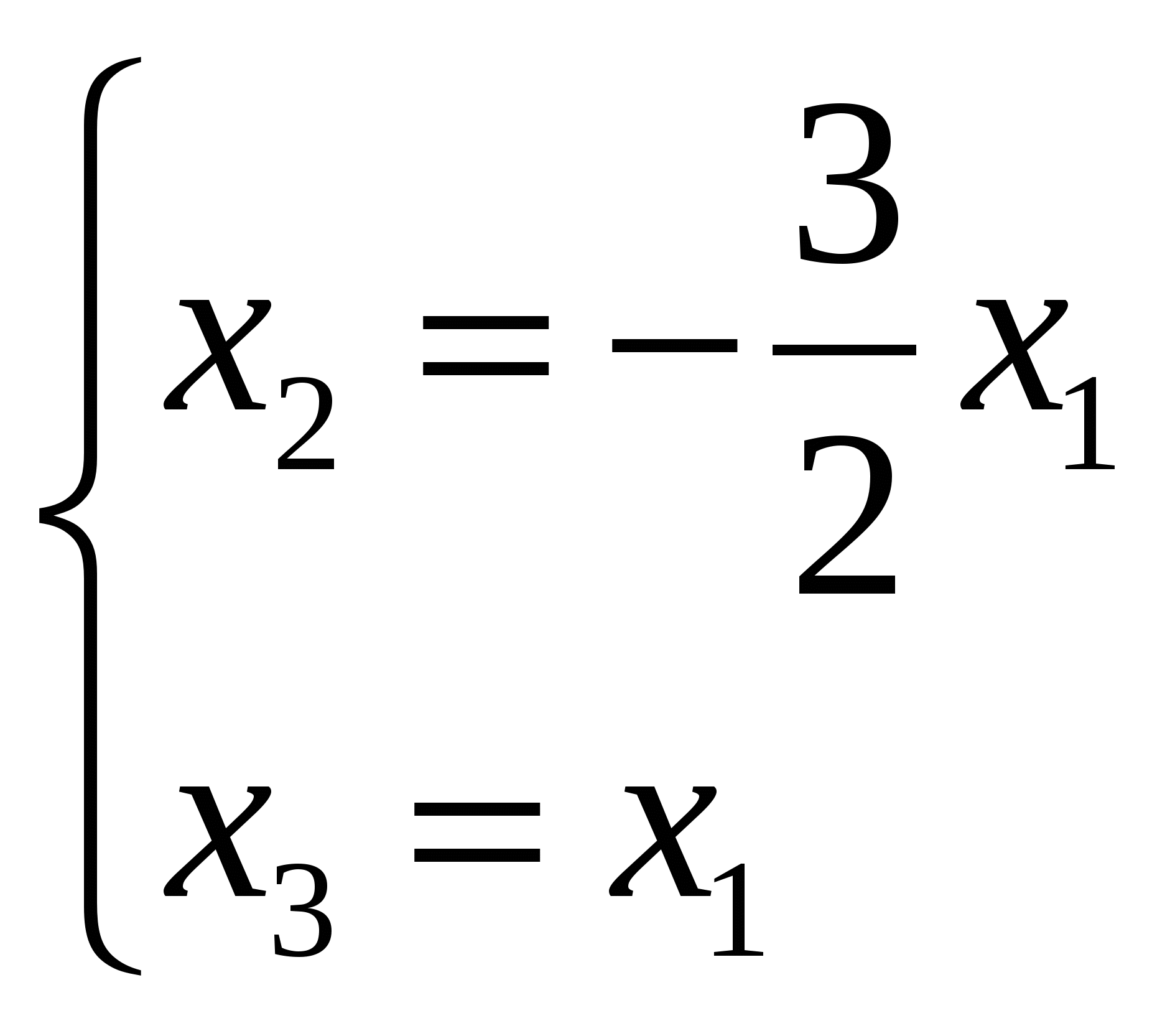 . Положим . Положим Для собственного числа λ2 =2 находим собственный вектор: 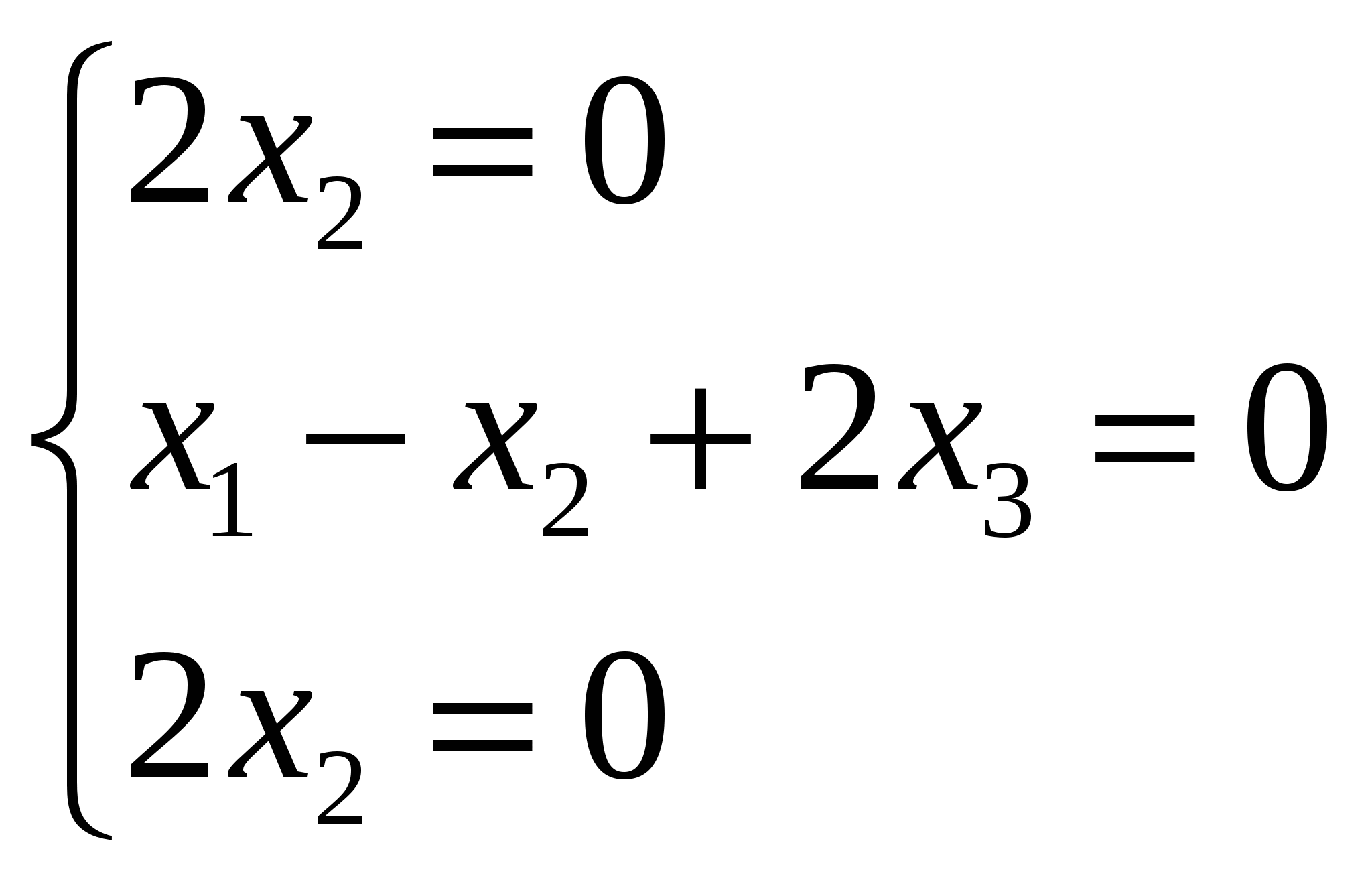 Отсюда собственный вектор Для собственного числа λ3 =4 находим собственный вектор:  Пусть x1 - свободное неизвестное, тогда выразим через него все остальные 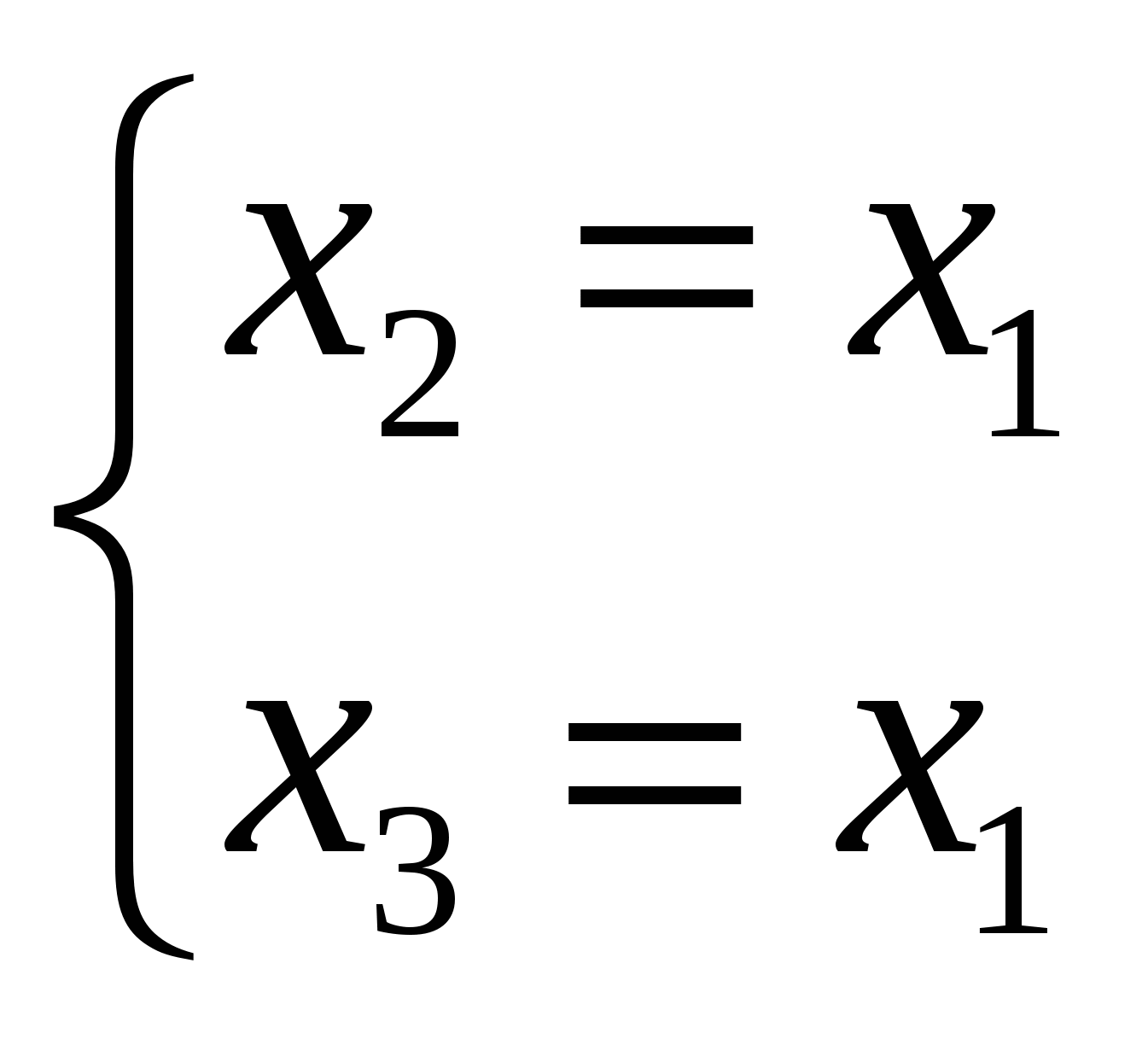 . Положим . Положим Ответ: Задание №8 Даны вершины треугольника АВС. Найти уравнение его сторон и точку пересечения высот. A(3,4), B(7,5), C(6,-4). Решение: Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле: Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: Чтобы найти точку пересечения высот, нужно сначала найти уравнения высот: Итак, уравнение высоты из вершины А(3,4) перпендикулярно прямой ВС: Итак, уравнение высоты из вершины В(7,5) перпендикулярно прямой АС: Итак, уравнение высоты из вершины С(6,-4) перпендикулярно прямой АВ: Чтобы найти точку пересечения высот нужно решить хотя бы одну систему уравнений:  Ответ: Задание №9 Привести уравнение кривой второго порядка к каноническому виду и построить линию. Решение: Сгруппируем переменные и выделим полные квадраты:  Задание №10 Построить график заданной кривой Решение: Приведем данное уравнение к следующему виду: 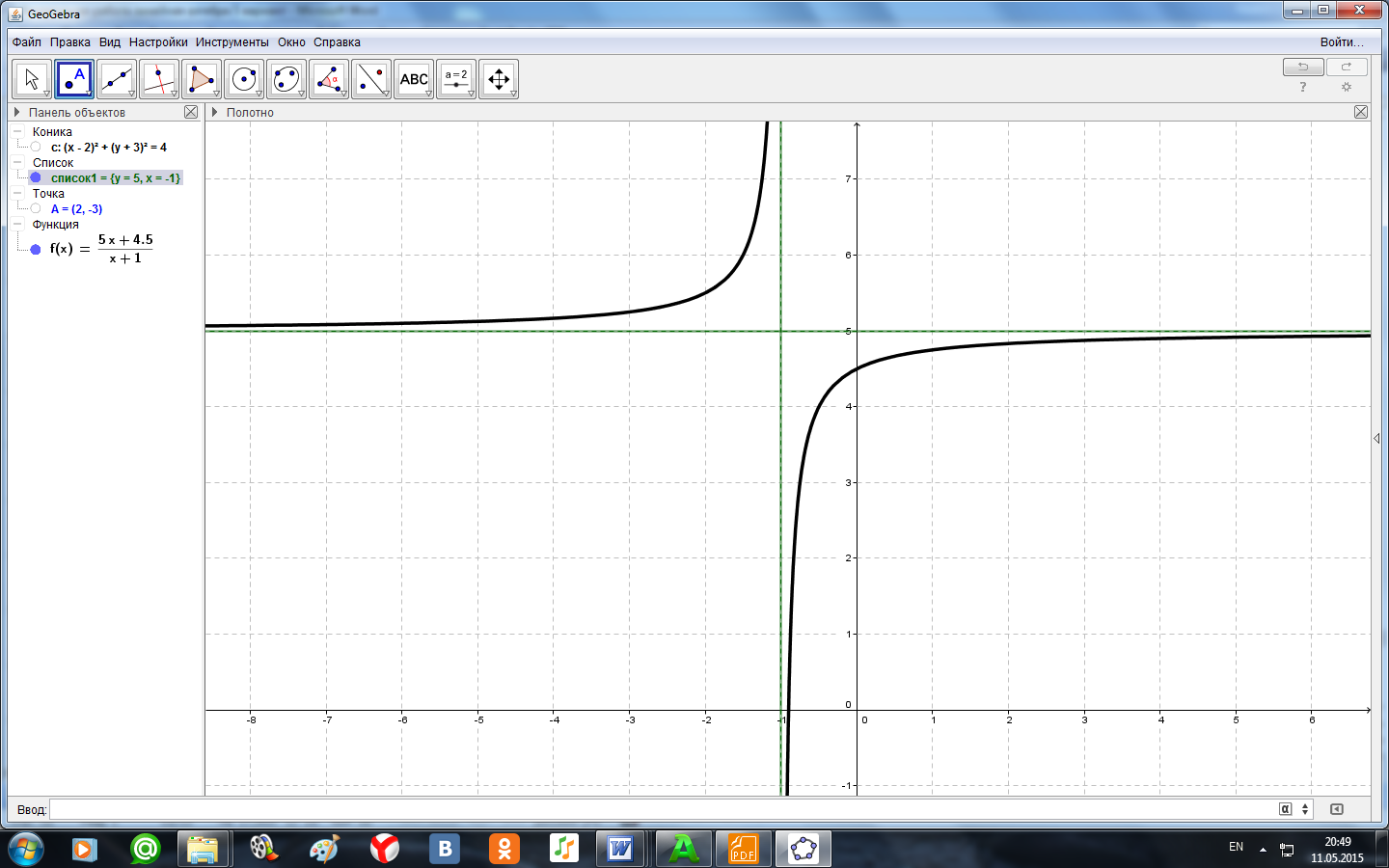 СПИСОК ЛИТЕРАТУРЫ 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.- М.: Наука, 1987.- 320с. 2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1975.- 272.с. 3. Карасев А.И. Аксютина З.М. Савельева Т.И. Курс высшей математики для экономических вузов. Ч.1, ч.2.-М.: Высшая школа, 1982.- 272с., 320с. 4. Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика. - Минск: Высшая школа, 1976.-720с. 5. Намм Р.В. Селезнева А.Н. Матричная алгебра: Учебное пособие.- Владивосток: Издательство дальневосточного университета, 1989.-116с. |