Решение. Заданная схема вала представлена на рисунке 1

• Название: Решение. Заданная схема вала представлена на рисунке 1
• Дата: 16.03.2022
• Размер: 6.07 Mb.
• Имя файла: Studbooks_140484.rtf
• Тип: Задача; #399264

Studlancer.net - закажи реферат, курсовую, диплом!

Задача 1
Определить из условий прочности необходимые размеры диаметров редукторного ступенчатого вала. Схема нагружения вала дана на рис. 1.

Исходные данные:

Мкр=0,2 кН·м.

a=30 мм.; b=60 мм.; c=100 мм.

D1=70 мм.; D2=120 мм.

[ϭ]p=120 МПа.

Требуется:

1. Вычертить в масштабе заданную схему вала с указанием размеров и величин нагрузок.

2. Определить окружные Р и радиальные усилия Т, приняв соотношение между ними Т=0.36Р.

3. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях.

4. Построить эпюру суммарных изгибающих моментов.

5. Построить эпюру крутящих моментов.

6. Используя энергетическую теорию прочности, определить диаметры вала на отдельных участках и округлить их до стандартных размеров.

7. Вычертить эскиз.

Решение.

1. Заданная схема вала представлена на рисунке 1.

2. Определим окружные Р и радиальные усилия Т.

Крутящий момент на валу вызывают силы Р1 и Р2.

Приведем силу P1 к центру тяжести сечения вала: тогда пара сил с моментом
М1 = P1D1/2

вызывает кручение, а сила P – изгиб вала в вертикальной плоскости.

В свою очередь, пара сил с моментом М2 =Р2D2/2 вызывает кручение в противоположную сторону, а сила в центре тяжести сечения вызывает изгиб.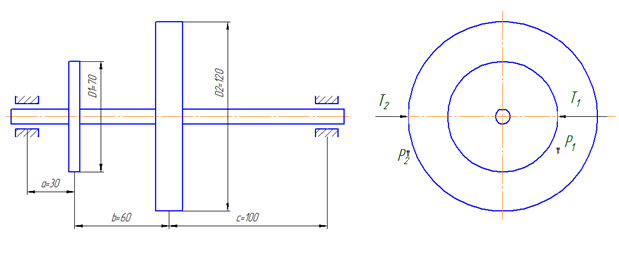


Рис. 1
Найдем окружные силы Р1 и Р2:

Радиальные усилия Т определим по формуле:

3. Построим эпюры изгибающих моментов.

Эпюра от действия сил в горизонтальной плоскости.

Определим опорные реакции:


Проверка:

Строим эпюру изгибающих моментов.

1-ый участок (0M=RB·z.
при z=0 M=0,

при z=0,1 M=0,002 кН·м.

2-ой участок (0M=RB·(0,1+z)+Т2·z.
при z=0 M=0,002 кН·м, при z=0,06 M=0,043 кН·м.

3-ий участок (0M=RА·z.

при z=0 M=0,

при z=0,03 M=0,043 кН·м.

Эпюра от действия сил в вертикальной плоскости.

Проверка:

Строим эпюру изгибающих моментов.

1-ый участок (0M=RB·z.
при z=0 M=0,

при z=0,1 M=0,25 кН·м.

2-ой участок (0M=RB·(0,1+z)-Р2·z.
при z=0 M=0,25 кН·м

при z=0,06 M=0,2 кН·м.

3-ий участок (0M=RА·z.
при z=0 M=0,

при z=0,03 M=0,2 кН·м.

Построим эпюру суммарных изгибающих моментов. Для этого нужно рассмотреть несколько сечений вала и определить в них суммарный изгибающий момент по формуле:

Отсюда получаем:

Моменты внутренних сил или крутящих моментов находят методом сечений. Сначала разбивают вал на участки (между соседними шкивами)

затем на каждом участке выбирают произвольное сечение. Крутящий момент в этом сечении равен алгебраической сумме моментов внешних сил, лежащих по одну сторону от сечения. В пределах каждого участка крутящий момент постоянен. Знак крутящего момента определяют по знаку внешних моментов: положительным считается направление против движения часовой стрелки при взгляде на сечение вала вдоль его оси. При этом можно рассматривать любую часть вала по одну сторону от сечения.

1) Для вала на рис.2 крутящие моменты по участкам:

1-ый участок:

М=0.

2-ой участок:

М=0,2 кН·м.

3-ий участок:

М=0.

Полученные эпюры изображены на рисунке 2.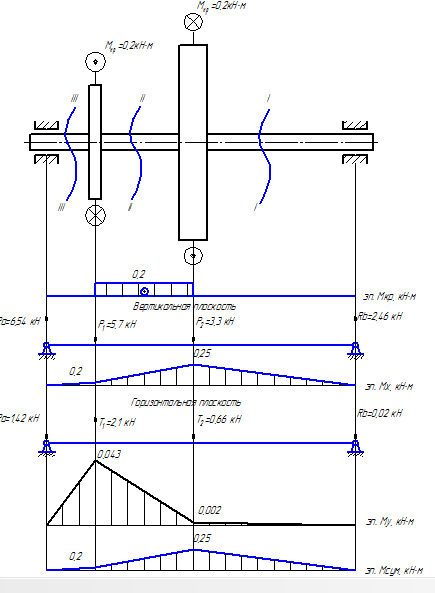


Рисунок 2 – Эпюры изгибающих и крутящих моментов.
Для подбора сечения применяем энергетическую гипотезу прочности:


Откуда

Принимаем d1=70 мм., d2=120 мм.
Задача 2
Стальной стержень (Е = 5 МПа) находится под действием продольной силы Р и собственного веса (γ = 7,8 т/м3). Найти перемещение сечения I-I (рис 3).


Рисунок 3 – Схема стального стержня

Исходные данные:

a=2,1 м.; b=2,1 м.; c=1,1 м.

F=11 см2.

Р=1,1 кН.

Решение:

Перемещение сечения I-I стержня при растяжении–сжатии определяется как сумма абсолютных деформаций 2 грузовых участков, заключенных между рассматриваемым и неподвижным (закрепленным) сечениями, т.е.

Для определения требуемых перемещений необходимо построить эпюру продольных сил.

1. В данной задаче нет необходимости определять реакцию заделки, так как один конец бруса свободный.

2. Разбиваем брус на грузовые участки 1, 2, 3.

3. В пределах каждого грузового участка проводим сечения на расстоянии zi от начала участка. (Рисунок 4)

4. В каждом сечении записываем функцию продольной силы Ni(zi). При этом рассматриваем свободную часть бруса.

5. Собственный вес стержней постоянного сечения учитывается как равномерно распределенная по длине каждого грузового участка нагрузка, направленная вниз. Интенсивность этой распределенной нагрузки равна весу части стержня единичной длины на данном участке.

1-ый участок (0≤z1≤1,1 м.)
N1= γFz1=78·103Н/м3·11·10-4м2· z1=85,8 z1;
при z1=0 N1=0

при z1=1,1 м. N1=94,4 Н.

2-ой участок (0≤z2≤2,1 м.)
N2= γF·1,1+ γ2F· z2=94,4+171,6 z2;
при z2=0 N2=94,4 Н;

при z2=2,1 м. N2=454,8 Н.

3-ий участок (0≤z3≤2,1 м.)
N3= γF·1,1+ γ2F· 2,1+Р+ γFz3=1554,8+85,8z3;
при z3=0 N3=1554,8 Н;

при z3=2,1 м. N3=1734,98 Н.

По вычисленным результатам строим эпюру N (рис. 4)


Рисунок 4 – Эпюра продольных сил

Определим перемещение сечения I-I стержня.

Так как при учете собственного веса на любом грузовом участке эпюра продольных сил имеет вид трапеции, то абсолютную деформацию этого участка можно вычислить по формуле:

где Ni(ср) – средняя линия трапеции.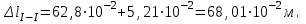





Задача 3
Для заданной сжатой стойки требуется:

1. Вычертить схему стойки.

2. Определить допускаемую нагрузку сжатой стойки, если требуемый коэффициент запаса устойчивости [ny] = 2. Материал стойки Ст. 3.

Е = 2,1·106 Па, [ϭ]= 1,4·108 Па.

Исследовать влияние изменения длины стойки на величину допускаемой нагрузки (определить допускаемую нагрузку при длине стойки 0,5l, 1,5l, 2l).

Схема стойки показана на рис. 5. Стойка представляет собой двутавр №10, длиной 2 м.



Рисунок 5 – Схема сжатой стойки.
Решение

Гибкость стержня определяется по формуле:

где μ - коэффициент приведения длины стержня, зависящий от способов закрепления концов. В данном случае μ=2.

imin - наименьший радиус инерции поперечного сечения стержня;

Jmin - наименьший осевой момент инерции поперечного сечения стержня; Jmin = 198 см4.

F - площадь поперечного сечения стержня; F = 12 см2.




При гибкости стержня, большей предельной: λ>λпред (для стали Ст.3, λпред = 100) критическую силу вычисляют по формуле Эйлера:

Если гибкость стержня λпред > λ > λ0 (для стали Ст.3 λ0 = 40) критическая сила вычисляется по эмпирической формуле Ясинского:


Ркр = F·ϭкр= F(a-bλ),
где а и b - коэффициенты, зависящие от материала. Для стали Ст.3 при гибкостях λ = 40-100, а = 310МПа, b =1,14МПа. Т.к. λпред > λ > λ0 (100 > 98 > 40), критическую силу вычисляем по эмпирической формуле Ясинского:
Ркр = 12(310-1,14·98)=237,9 кН.
Допускаемая нагрузка: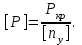



При длине стойки 0,5l = 1 м. гибкость равна:

Критическую силу вычисляем по эмпирической формуле Ясинского:

Ркр = 12(310-1,14·49)=304,9 кН.
Допускаемая нагрузка:

При длине стойки 1,5l = 3 м. гибкость равна:

При гибкости стержня, большей предельной: λ>λпред (147>100) критическую силу вычисляем по формуле Эйлера:

Допускаемая нагрузка:

При длине стойки 2l = 4 м. гибкость равна:

Критическую силу вычисляем по формуле Эйлера:


Допускаемая нагрузка:

На основании проведенных выше расчетов можно сделать вывод о том, что при увеличении длины стойки, величина допускаемой нагрузки уменьшается.
Задача 4
Стальной кубик (рис. 5) находится под действием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю). Требуется найти:

1. главные напряжения и направление главных площадок;

2. максимальные касательные напряжения, равные наибольшей полуразности главных напряжений;

3. относительные деформации εх, εy, εz;

4. относительное изменение объема;

5. удельную потенциальную энергию деформаций.

Исходные данные:
ϭх=10 МПа, ϭy=10МПа, τх=80 МПа.
1. Постановка знаков заданных нормальных и касательных напряжений:
σх = σу = 10 МПа, ("плюс" – растяжение),

τу = –80 МПа ("минус" – против хода часовой стрелки).



Рисунок 6
2. Вычисление главных напряжений.

Соблюдая условие σ1 ≥ σ2 ≥ σ3, выпишем числовые значения главных напряжений:
σ max = σ1 = 10 + 80 = 90 МПа,

σ min = σ3 = 10 – 80 = –70 МПа, σ2 = 0 (по условию задачи).
Проверка:
σx +σy =σ1 +σ3 = 10 + 10 = 90 – 70 = 20 МПа.
Определяем угол наклона главных площадок к заданным:


Угол положительный, поэтому заданные площадки должны быть повернуты против хода часовой стрелки и на полученных главных площадках показываем главные напряжения.

3. Определение максимального и минимального касательных напряжений на площадках сдвига по формуле:

4. Вычислим относительные деформации используя формулы обобщенного закона Гука:

5. Изменение объема определяется по формуле:

6. Удельная потенциальная энергия определяется по формуле:


Задача 5
Подобрать прочные размеры и оценить экономичность подобранных сечений. Схема балки приведена на рисунке 6.

Исходные данные:
a=2 м.; b=3,2 м.; c=1,8 м.; l=10 м.

М=10 кН·м.; Р=16 кН.; q=22 кН/м.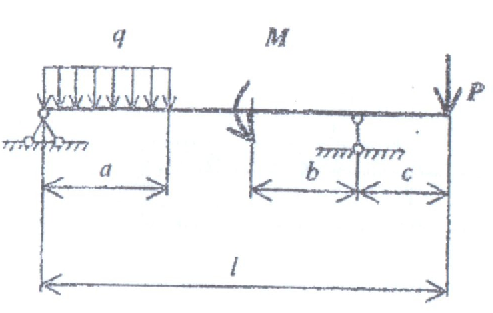


Рисунок 7 – Схема балки
Решение:

Построим эпюры M и Q:

1. Определим реакции опор:


Проверка:

Сечения проведем бесконечно близко в начале и в конце грузовых участков, на которых отсутствует распределенная нагрузка q. Дополнительное сечение проведем по середине участка, где имеется q.

Вычислим значения Q и М в этих сечениях. Для сечений 1–1, 2–2, 3–3, 4-4 будем рассматривать левую отсеченную часть, а для остальных – правую часть.
Q1-1=RA=37,25 кН.

Q3-3=RA-q2=37,25-22·2=-6,8 кН.

Q4-4= Q5-5= Q6-6= Q7-7=-RB+P=-23,65+16=-6,8 кН.

Q8-8= Q9-9=P=16 кН.

M1-1=0.

M2-2=RA1-q1·0,5=37,25·1-22·1·0,5=26,25 кН·м.

M3-3= M4-4=RA2-q2·1=37,25·2-22·2·1=30,5 кН·м.

M5-5=RA5-q2·4=37,25·5-22·2·4=10,25 кН·м.

M6-6=RВ3,2-Р·5=23,65·3,2-16·5=0,25 кН·м.

M7-7= M8-8=-Р·1,8=-16·1,8=-28,8 кН·м.

M9-9=0.
По полученным результатам строим эпюры М и Q (рисунок 8).


Рисунок 8 – Эпюры Q и M
Эпюру М строим со стороны растянутых волокон, т.е. значения М со знаком "минус" откладываем вверх. Из эпюры Q видно, что экстремальное значение изгибающего момента на 1-м грузовом участке будет в сечении на расстоянии х0, т.е. там, где Q(х0) = 0. Из этого условия находим величину х0:
Q(х0)=RA-qх0=37,25-22· х0=0. х0=37,25/22=1,7 м.
Вычисляем в этом сечении величину Мэкстр:


Для заданной балки рассмотрим четыре варианта сечений: круглое, прямоугольное(h/b=2), двутавровое и из двух швеллеров, приняв допустимое напряжение [ϭ]=160 МПа.

Из условия прочности по нормальным напряжениям ϭmax=Mmax/Wx≤[ϭ] определяем требуемый момент сопротивления поперечного сечения.

вал балка сечение нагрузка

Wx≥ Mmax/[ϭ]=31,5·103 /160·106=197 см3.
по которому подбираем конкретные сечения.

Круг.

По ГОСТ 6636-69 подбираем нормализованное значение d=130 мм. Тогда А=π d2/4= π·132/4=132,7 см2.

Прямоугольник.

Wx=b·(2b)2/6=2b3/3. Отсюда

Принимаем b=67 мм. Тогда А2=2b2=2·6,72=89,78 см2.

Двутавр.

По ГОСТ 8239-89 выбираем двутавр №22 с Wx=230 см3 и А3=30 см2.

Два швеллера.

По ГОСТ 8240-89 выбираем два швеллера №18 с Wx=2·121=242 см3 и А4=2·20,7=41,4 см2.

Масса балки определяется как произведение плотности материала на ее объем m=ρAl т.е. при прочих равных условиях расход материала зависти только от площади поперечного сечения. Сравнивая массы балок:

m1: m2: m3: m4= А1: А2: А3: А4=1:0,68:0,23:0,31,

заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера) достигается экономия, равная соответственно 32%, 77% и 69%.

Размещено на Studbooks.net