Динамика точки. Решение Запишем для этой точки дифференциальные уравнение в проекциях на декартовы оси координат
 Скачать 37.28 Kb.
|
|
Вариант №18 Материальная точка массой m, движется под действием сил, равнодействующая которых зависит от времени, координат точки и ее скорости: 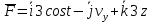 Определить уравнения движения точки в координатной форме при заданных начальных условиях. x0 = -1; y0 = 3; z0 = 2; vx0 = 2; vy0 = 3; vz0 = 2; m = 3 кг Решение Запишем для этой точки дифференциальные уравнение в проекциях на декартовы оси координат  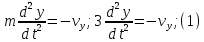  Первое уравнение системы (1) можно представить в виде двух уравнений первого порядка 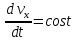 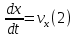 В первом уравнении связаны две переменные величины: проекция скорости на ось x и время. Разделяя переменные, получим 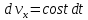 Слева и справа от знака равенства стоят дифференциалы некоторых функций. Если дифференциалы равны, то и интегралы равны с точностью до постоянной интегрирования  После интегрирования получим  т.е. зависимость проекции скорости точки на ось x от времени. Из второго уравнения системы (2) получим 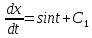 Снова, разделяя переменные, получим 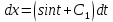 После интегрирования получим 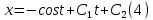 Постоянные C1 и C2 определим по начальным условиям. Подставляя в выражение (4) значение координаты x0 = -1 при t = 0, получаем 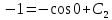 отсюда С2= 0 Постоянную C1 определим, подставляя в (3) значение Vx=2 при t = 0: 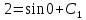 отсюда С1= 2 Таким образом, решение первого уравнения системы (1) имеет вид 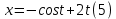 Второе уравнение системы (1) также представляем в виде двух уравнений 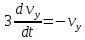 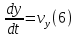 Разделяя переменные в первом уравнении, получим  Решая относительно Vy , получим  Учитывая второе уравнение системы (6), снова получаем 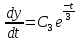 Разделяя переменные и интегрируя, получим 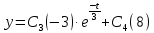 Постоянные C3 и C4 определяем по начальным условиям. Из (7) 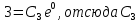 = 3Из (8) 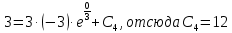 Таким образом, решение второго уравнения системы (1) имеет вид 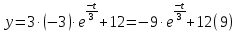 Третье уравнение системы (1) также представляем в виде двух уравнений 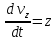  В первом уравнении системы (16), связаны три переменных величины: скорость, время и координата точки. Чтобы разделить переменные необходимо исключить одну из них. Произведем замену 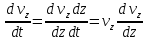 Тогда первое уравнение (10) примет вид 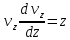 Теперь можно разделить переменные 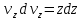 Интегрируя, получим  Решая относительно vz, получим  По начальным условиям найдем постоянную C5 . 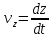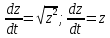Подставляя в (11) vz0 = 2 и z0 =2, получим  Учитывая, что  выражение (11) запишется в виде Разделив переменные, приведем его к виду 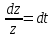 Интегрируя, получим  Решая относительно z, получим 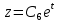 Постоянную C6 найдем по начальным условиям. При t = 0 z0 = 2 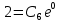 отсюда C6 =2 Таким образом, решение третьего уравнения системы (1) будет иметь вид   Окончательно уравнения движения точки в координатной форме имеют вид: 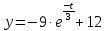 |