1образцы ВПР для 5 классаdocx. Решение. Запишем сначала все трехзначные числа меньше 201, кратные 20 100, 120, 140, 160, 180, 200. Из них кратны 30 числа 120, 180
 Скачать 332.03 Kb.
|
|
1. Задание 1 № 31 Приведите пример натурального трехзначного числа, меньшего 201, которое делится на 20 и 30. Решение. Запишем сначала все трехзначные числа меньше 201, кратные 20: 100, 120, 140, 160, 180, 200. Из них кратны 30 числа 120, 180. Ответ: 120 или 180. 2. Задание 2 № 58 Какое число нужно написать в числителе, чтобы равенство стало верным?  Решение. Сократим дробь:  Следовательно, это число 2. Ответ: 2. 3. Задание 3 № 890 Выберите и запишите наименьшую из десятичных дробей: 10,24; 9,08; 9,7; 9,18 Решение. Расставим числа в порядке возрастания:  Ответ: 9,08. 4. Задание 4 № 1369 В магазин завезли овощи. Три седьмых всех овощей — помидоры, а две седьмых всех овощей — огурцы. Сколько килограммов помидоров завезли в магазин, если огурцов завезли 84 кг? Решение. Заметим, что масса помидоров составляет  от массы огурцов. Вычислим, сколько килограммов помидоров завезли в магазин:  Ответ: 126. 5. Задание 5 № 153 Найдите значение выражения  Решение. Найдем значение выражения: 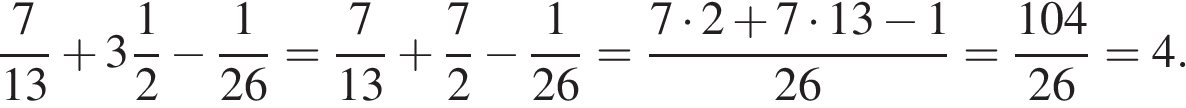 Ответ: 4. 6. Задание 6 № 179 В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа? Запишите решение и ответ. Решение. Выясним, сколько будет весить руда, содержащая 73,5 т железа:  т.Найдем теперь, сколько примесей будет содержаться в руде: 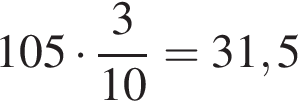 т.Допускается другая последовательность действий, обоснованно приводящая к верному ответу. Ответ: 31,5 т. Примечание. Задачу можно решить, составив пропорцию: 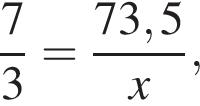 где х — количество примеси в руде. Таким образом:  тонна примесей.7. Задание 7 № 208 Пачка мороженого стоит 20 руб. Сколько денег было у Ани, если она купила 5 пачек мороженого и у неё осталось 11 руб? Ответ дайте в руб. Решение. Всего денег было у Ани:  руб.Ответ: 111. 8. Задание 8 № 233 Мама получила премию 180 руб. На подарок дочери она потратила 1% этой премии. Сколько рублей стоит подарок? Решение. Найдем 1% от 180 рублей:  руб.Ответ: 1,8. 9. Задание 9 № 269 Найдите значение выражения 7225 : 85 + 64 · 2345 − 248838 : 619. Запишите решение и ответ. Решение. Решение:   Ответ: 149763. 10. Задание 10 № 300 Килограмм масла стоил 240 рублей. После подорожания цена выросла на 1/8, но потом уменьшилась на 1/9. Сколько после этого стоит килограмм масла? Запишите решение и ответ. Решение. 1) 240 : 8 = 30 (1/8 прежней стоимости) 2) 240 + 30 = 270 (стоимость масла после подорожания) 3) 270 : 9 = 30 (1/9 новой стоимости масла) 4) 270 − 30 = 240 Ответ: 240 руб. 11. Задание 11.1 № 22 На диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте на вопрос.  Какое озеро занимает третье место по величине площади среди представленных на диаграмме? В ответе укажите одно слово — название озера. Решение. Необходимо считать от наибольшего значения. Из диаграммы видно, что третье место по величине занимает Светлое озеро. Ответ: Светлое. 12. Задание 11.2 № 450 На диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте на вопрос. Напишите названия самого маленького и самого большого по площади озёр. Ответ запишите без пробелов, запятых или других дополнительных символов. Решение. Из диаграммы видно, что самое маленькое по площади озеро — Круглое, самое большое — Глубокое. Ответ: Круглое Глубокое. 13. Задание 12.1 № 407 На плане одного из районов города клетками изображены кварталы, каждый из которых имеет форму квадрата со стороной 150 м. Ширина всех улиц в этом районе — 25 м.  Найдите длину пути от точки А до точки В, изображенных на плане.В ответе укажите только число. Решение. Длина пути равна: 25 + 150 + 25 + 150 + 150 + 25 + 150 + 150 + 25 + 25 = 875 м. Ответ: 875 м. 14. Задание 12.2 № 514 На плане одного из районов города клетками изображены кварталы, каждый из которых имеет форму квадрата со стороной 150 м. Ширина всех улиц в этом районе — 25 м. Изобразите на плане маршрут, который начинается и заканчивается в точке С и имеет длину не меньше 1 км 650 м и не больше 1 км 800 м. Решение. Один из возможных вариантов:  Длина данного маршрута составляет 1750 м. 15. Задание 13 № 24 Из одинаковых кубиков сложили фигуру, а затем положили на неё сверху еще две такие же фигуры (рисунок 1). После этого сверху вытащили ровно один кубик (рисунок 2).  Из скольких кубиков состоит фигура, изображенная на рисунке 2? Решение. В одном слое 4 · 3 = 12 кубиков. Таких слоев 3: 3 · 12 = 36. После вытаскивания одного кубика, получаем: 36 - 1 = 35 кубиков. Ответ: 35. 16. Задание 14 № 379 На карточках написаны различные двузначные числа. Сколько карточек нужно взять не глядя, чтобы по крайней мере одно из чисел делилось на 2 или на 7? Запишите решение и ответ. Решение. Решение: В худшем случае, выбирая карточки, мы можем иметь только нечётные числа — их 45, следовательно, 46 карточка будет наверняка делиться на 2. Двухзначных чисел, которые делятся на 7 — тринадцать. Из них 6 — нечетных. Следовательно, 45 - 6 = 39 неудачных исходов может быть до того, как мы вытянем число, которое делится на 7. Таким образом, достаточно вытянуть 40 карточек, так как в условии сказано или на 2, или на 7. Ответ: 40. Вариант № 1394428 1. Задание 1 № 36 Сколько уникальных цифр использовано для записи числа 640046? Решение. В записи числа 640046 использовано три уникальных цифры — 0, 4 и 6. Ответ: 3. 2. Задание 2 № 60 Какое число нужно написать в числителе, чтобы равенство стало верным?  Решение. Сократим дробь:  Следовательно, это число 1. Ответ: 1. 3. Задание 3 № 91 Запишите цифрами десятичную дробь: «ноль целых восемьсот четыре десятитысячных». Решение. Ответ: 0,0804. 4. Задание 4 № 121 Длина дороги 20 км. Заасфальтировали  дороги. Сколько километров осталось заасфальтировать?Решение. Для начала посчитаем длину заасфальтированной дороги. Так как заасфальтировали две части из пяти, то сначала найдём одну часть:  км. Тогда две части от всей дороги:  Если заасфальтировали 8 из 20 км, то осталось  км.Ответ: 12. 5. Задание 5 № 146 При каком значении x верно равенство:  Решение. Найдем х:  Ответ: 660. 6. Задание 6 № 176 Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени? Запишите решение и ответ. Решение. Вычислим, сколько масла можно получить из одного кг хлопкового семени:  Найдем теперь, сколько масла получится из 7 кг хлопкового семени: 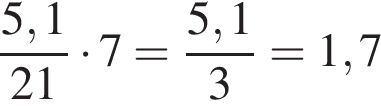 кг.Допускается другая последовательность действий, обоснованно приводящая к верному ответу. Ответ: 1,7 кг. 7. Задание 7 № 204 В коробку помещается дюжина вилок. В такие коробки надо разложить 250 вилок. Сколько полных коробок получится? Решение. Дюжина — это число 12. Получим:  Полных коробок получится 20.Ответ: 20. 8. Задание 8 № 1213 В пятницу на выставке было на 20% посетителей больше, чем в четверг. Сколько посетителей было на выставке в четверг, если в пятницу выставку посетило 1800 человек? Решение. Пусть в четверг на выставке было x человек. Так как в пятницу на выставке было на 20% посетителей больше, чем в четверг, то можно составить такое уравнение  Таким образом, в четверг посетителей было: Ответ: 1500. 9. Задание 9 № 268 Найдите значение выражения 8607 + 7605 + (376012 − 83314) : 414 : 7. Запишите решение и ответ. Решение. Решение:    Ответ: 16313. 10. Задание 10 № 298 2 пары туфель стоят в магазине 1380 рублей. Сколько нужно заплатить за 3 пары сапог, если стоимость пары сапог на 370 руб. дороже, чем пары туфель? Запишите решение и ответ. Решение. 1) 1380 : 2 = 690 (стоит 1 пара туфель) 2) 690 + 370 = 1060 (стоит 1 пара сапог) 3) 1060 · 3 = 3180 Ответ: 3180 руб. 11. Задание 11.1 № 322 На игре КВН судьи поставили оценки командам за конкурсы:
Какая команда набрала наибольшее число баллов в конкурсе «Приветствие»? В ответе укажите одно слово — название команды в именительном падеже. Решение. Наибольшее число баллов в конкурсе «Приветствие»набрала команда «Шарм». Ответ: Шарм. 12. Задание 11.2 № 477 На игре КВН судьи поставили следующие оценки командам за конкурсы.
Сколько суммарно баллов набрали команды за музыкальный конкурс? Решение. За музыкальный конкурс команды набрали: 25 + 23 + 27 + 29 = 104 балла. Ответ: 104. 13. Задание 12.1 № 410 На рисунке изображён план участка, вокруг которого нужно построить забор.  Какова должна быть длина забора (в м)? Решение. Найдем длину забора: 10 + 20 + 25 + 5 + 17 + 15 + 30 + 15 + (25 + 17 − 30 − 10) + 15 = 154 м. Ответ: 154. 14. Задание 12.2 № 521 На рисунке изображён план сада. Штриховой линией показана деревянная дорожка, которую нужно выложить, её ширина 0,5 м.  Сколько брусков потребуется для того, чтобы выложить дорожку, если один брусок имеет размеры 0,5 x 0,5 м? Решение. Найдем площадь дорожки:   м2. Тогда понадобится брусков:  Ответ: 67. Примечание. Обращаем внимание читателей, что часть верхней границы сада, примыкающей к левой границе, находится выше, чем часть верхней границы, примыкающей к правой границе сада. Разность уровней составляет 1 метр. Рисунок корректен и позволяет верно решить задачу. 15. Задание 13 № 375  От куба отрезали часть так, как это показано на рисунке. Сколько у получившегося многогранника граней? Решение. У данного многогранника 7 граней. Ответ: 7. 16. Задание 14 № 380 Два охотника отправились одновременно навстречу друг другу из двух деревень, расстояние между которыми 18 км. Первый шёл со скоростью 5 км/ч, а второй — 4 км/ч. Первый охотник взял с собой собаку, которая бежала со скоростью 8 км/ч. Собака сразу же побежала навстречу второму охотнику, встретила его, повернула и с той же скоростью побежала навстречу своему хозяину. Встретила его, повернула и побежала навстречу второму охотнику и т. д. Так она бегала от одного охотника к другому, пока те не встретились. Сколько километров пробежала собака? Запишите решение и ответ. Решение. Решение: скорость сближения охотников равна 5 + 4 = 9 км/ч. Следовательно, встретятся они через 18 : 9 = 2 часа. За 2 часа собака пробежит: 2 · 8 = 16 км. Ответ: 16 км. Вариант № 1394429 1. Задание 1 № 34 Напишите число, в котором 7 тысяч 8 единиц 0 сотен 0 десятков. Решение. Запишем число в виде: a · 1000 + b · 100 + c · 10 + d. Получаем: 7 · 1000 + 0 · 100 + 0 · 10 + 8 = 7000 + 0 + 0 + 8 = 7008. Ответ: 7008. 2. Задание 2 № 62 Какое число нужно написать в числителе, чтобы равенство стало верным?  Решение. Сократим дробь:  Следовательно, это число 2. Ответ: 2. 3. Задание 3 № 112 Запишите в виде десятичной дроби частное 61 : 1000. Решение. Запишем в виде десятичной дроби:  Ответ: 0,061. 4. Задание 4 № 127 На приобретение костюма покупатель израсходовал  своих денег. Сколько рублей было у покупателя, если костюм стоил 120 р?Решение. Костюм стоил 120 р, и это составляет всех денег. Тогда получим:  р было у покупателя.Ответ: 150. 5. Задание 5 № 147 При каком значении x верно равенство:  Решение. Найдем х:  Ответ: 3036. 6. Задание 6 № 1291 Из двух городов одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 40 км/ч, другой — со скоростью 60 км/ч. На сколько километров больше проехал второй автомобиль до места их встречи, если расстояние между городами 400 км? Запишите решение и ответ. Решение. Найдём скорость сближения двух автомобилей: 40 + 60 = 100 км/ч. Значит, автомобили ехали до места встречи  часов. Первый автомобиль проехал 40 · 4 = 160 км. Второй автомобиль проехал 60 · 4 = 240 км. Следовательно, второй автомобиль проехал на 240 − 160 = 80 км больше, чем первый.Ответ: 80 км. 7. Задание 7 № 209 На пошив одного костюма нужно 3 м ткани. Сколько метров ткани было в рулоне, если пошили 5 костюмов и осталось 2 м ткани? Решение. В рулоне было  м ткани.Ответ: 17. 8. Задание 8 № 242 Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге? Решение. Получим:  страниц в книге.Ответ: 600. 9. Задание 9 № 1154 Найдите значение выражения 162 + 20 · 37− 5621 : 11. Запишите решение и ответ. Решение. 1) 20 · 37 = 740; 2) 5621 : 11= 511; 3) 162 + 740 = 902; 4) 902 − 511 = 391. Ответ: 391. 10. Задание 10 № 315 В магазине продается несколько видов куриного филе в различных упаковках и по различной цене. Какова наименьшая цена в расчёте на 1 кг куриного филе среди данных в таблице видов?
Запишите решение и ответ. Решение. Рассчитаем цену за 1 г и умножим её на 1000. Для первого вида: 54 : 300 · 1000 = 180 рублей. Для второго вида: 43 : 250 · 1000 = 172 рубля. Для третьего вида: 41 : 250 · 1000 = 164 рубля. Для четвёртого вида: 33 : 200 · 1000 = 165 рублей. Таким образом, наименьшая цена составляет 164 рубля. Ответ: 164 руб. 11. Задание 11.1 № 326 Баскетбольная команда детской спортивной школы встречалась с командами нескольких школ. Количество очков, набранных игроками, тренер записывал в таблицу. Используя таблицу, ответьте на вопрос.
Сколько очков набрал Владимир в третьей игре? Решение. Владимир в третьей игре набрал 7 очков. Ответ: 7. 12. Задание 11.2 № 457 Баскетбольная команда детской спортивной школы встречалась с командами нескольких школ. Количество очков, набранных игроками, тренер записывал в таблицу. Используя таблицу, ответьте на вопрос.
В какой игре мальчики вместе набрали больше всего очков? В ответе укажите одно число — номер игры. Решение. Найдем общее количество очков в каждой из игр: Первая игра: 2 + 9 + 9 = 20 очков. Вторая игра: 6 + 5 + 8 = 19 очков. Третья игра: 8 + 2 + 7 = 17 очков. Четвертая игра: 4 + 10 + 9 = 23 очка. Таким образом, наибольшее количество очков мальчики набрали в четвёртой игре. Ответ: 4. 13. Задание 12.1 № 414 На рисунке изображён план сада, вдоль периметра которого нужно вырыть канаву. Какова будет длина канавы? В ответе укажите только число в метрах. Решение. 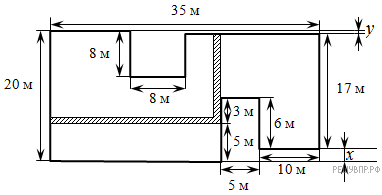 Введём обозначения как показано на рисунке. Заметим, что длина x = 3 + 5 − 6 = 2 м. Тогда длина y = 20 − 17 − 2 = 1 м. Найдем длину канавы: 20 + 35 + 8 + (8 − 1) + 17 + 10 + 5 + 6 + 3 + 5 + (35 − 5 − 10) = 136 м.Ответ: 136. 14. Задание 12.2 № 515 На плане одного из районов города клетками изображены кварталы, каждый из которых имеет форму квадрата со стороной 120 м. Ширина всех улиц в этом районе — 40 м.  Изобразите на плане маршрут, который начинается и заканчивается в точке С и имеет длину не меньше 1 км 120 м и не больше 1 км 220 м. Решение. Один из возможных вариантов: 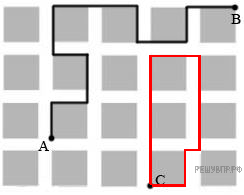 Длина данного маршрута составляет 1 км 200 м. 15. Задание 13 № 352 Найдите объём коробки, имеющей форму прямоугольного параллелепипеда. Ответ дайте в см3.  Решение. Объём коробки равен произведению всех трёх её измерений, т. е. 9 · 30 · 4 = 1080 см3. Ответ: 1080. 16. Задание 14 № 393 К двузначному числу прибавили 5, и сумма оказалась кратной 5. Когда от него отняли 3, то разность оказалась кратной 3. Когда его поделили на 2, то оказалось, что и частное делится на 2. Найдите это число. Запишите решение и ответ. Решение. Решение: если число стало делиться на 5 при прибавлении 5, оно и было кратно 5. Если от числа отняли 3, и разность делится на 3, значит, оно и было кратно 3. Если число поделили на 2, и его частное тоже поделили на 2, это значит, что число кратно 4. Таким образом, число кратно 5, 3 и 4. Следовательно:  Ответ: 60. |