Контрольная. Онлайн. Симплексметод Определим максимальное значение целевой функции
 Скачать 84.16 Kb. Скачать 84.16 Kb.
|
|
Симплекс-метод Определим максимальное значение целевой функции F(X) = 126x1+118x2+108x3 при следующих условиях-ограничений. 0.6x1+0.5x2+0.8x3≤800 0.3x1+0.4x2+0.4x3≤600 0.1x1+0.1x2≤108 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 0.6x1+0.5x2+0.8x3+x4 = 800 0.3x1+0.4x2+0.4x3+x5 = 600 0.1x1+0.1x2+x6 = 108 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана. Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,800,600,108) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (800 : 0.6 , 600 : 0.3 , 108 : 0.1 ) = 1080 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (0.1) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x6 в план 1 войдет переменная x1. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 1080, x3 = 325 F(X) = 126*0 + 118*1080 + 108*325 = 162540 Задание №2 Математическая модель транспортной задачи: F = ∑∑cijxij, (1) при условиях: ∑xij = ai, i = 1,2,…, m, (2) ∑xij = bj, j = 1,2,…, n, (3) xij ≥ 0 Запишем экономико-математическую модель для нашей задачи. Переменные: x11 – количество груза из 1-го склада в 1-й магазин. x12 – количество груза из 1-го склада в 2-й магазин. x13 – количество груза из 1-го склада в 3-й магазин. x21 – количество груза из 2-го склада в 1-й магазин. x22 – количество груза из 2-го склада в 2-й магазин. x23 – количество груза из 2-го склада в 3-й магазин. x31 – количество груза из 3-го склада в 1-й магазин. x32 – количество груза из 3-го склада в 2-й магазин. x33 – количество груза из 3-го склада в 3-й магазин. x41 – количество груза из 4-го склада в 1-й магазин. x42 – количество груза из 4-го склада в 2-й магазин. x43 – количество груза из 4-го склада в 3-й магазин. x51 – количество груза из 5-го склада в 1-й магазин. x52 – количество груза из 5-го склада в 2-й магазин. x53 – количество груза из 5-го склада в 3-й магазин. Ограничения по запасам: x11 + x12 + x13 ≤ 280 (для 1 базы) x21 + x22 + x23 ≤ 140 (для 2 базы) x31 + x32 + x33 ≤ 80 (для 3 базы) x41 + x42 + x43 ≤ 70 (для 4 базы) x51 + x52 + x53 ≤ 210 (для 5 базы) Ограничения по потребностям: x11 + x21 + x31 + x41 + x51 = 300 (для 1-го магазина) x12 + x22 + x32 + x42 + x52 = 150 (для 2-го магазина) x13 + x23 + x33 + x43 + x53 = 330 (для 3-го магазина) Целевая функция: 7x11 + 10x12 + 10x13 + 5x21 + 4x22 + 8x23 + 6x31 + 6x32 + 9x33 + 6x41 + 6x42 + 8x43 + 3x51 + 2x52 + 3x53 → min Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 280 + 140 + 80 + 70 + 210 = 780 ∑b = 300 + 150 + 330 = 780 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Занесем исходные данные в распределительную таблицу. 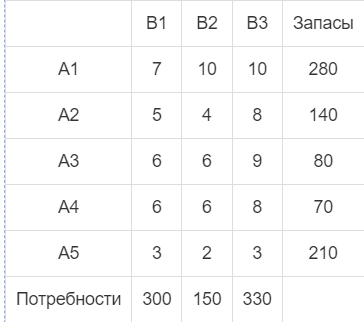 1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Искомый элемент равен c52=2. Для этого элемента запасы равны 210, потребности 150. Поскольку минимальным является 150, то вычитаем его. x52 = min(210,150) = 150.
Искомый элемент равен c51=3. Для этого элемента запасы равны 60, потребности 300. Поскольку минимальным является 60, то вычитаем его. x51 = min(60,300) = 60.
Искомый элемент равен c21=5. Для этого элемента запасы равны 140, потребности 240. Поскольку минимальным является 140, то вычитаем его. x21 = min(140,240) = 140.
Искомый элемент равен c31=6. Для этого элемента запасы равны 80, потребности 100. Поскольку минимальным является 80, то вычитаем его. x31 = min(80,100) = 80.
Искомый элемент равен c41=6. Для этого элемента запасы равны 70, потребности 20. Поскольку минимальным является 20, то вычитаем его. x41 = min(70,20) = 20.
Искомый элемент равен c43=8. Для этого элемента запасы равны 50, потребности 330. Поскольку минимальным является 50, то вычитаем его. x43 = min(50,330) = 50.
Искомый элемент равен c13=10. Для этого элемента запасы равны 280, потребности 280. Поскольку минимальным является 280, то вычитаем его. x13 = min(280,280) = 280.
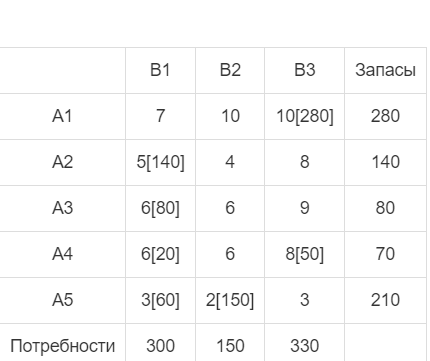 В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи. 2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным. Значение целевой функции для этого опорного плана равно: F(x) = 10*280 + 5*140 + 6*80 + 6*20 + 8*50 + 3*60 + 2*150 = 4980 Задание №3
Критерий Байеса (максимального математического ожидания) По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r. Считаем значения ∑(aijpj) ∑(a1,jpj) = 40*0.35 + 50*0.3 + 30*0.35 = 39.5 ∑(a2,jpj) = 50*0.35 + (-48)*0.3 + 20*0.35 = 10.1 ∑(a3,jpj) = 30*0.35 + 56*0.3 + (-24)*0.35 = 18.9 ∑(a4,jpj) = 18*0.35 + 60*0.3 + 80*0.35 = 52.3
Выбираем из (39.5; 10.1; 18.9; 52.3) максимальный элемент max=52.3 Вывод: выбираем стратегию N=4. Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: a = min(max rij) Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы. 1. Рассчитываем 1-й столбец матрицы рисков. r11 = 50 - 40 = 10; r21 = 50 - 50 = 0; r31 = 50 - 30 = 20; r41 = 50 - 18 = 32; 2. Рассчитываем 2-й столбец матрицы рисков. r12 = 60 - 50 = 10; r22 = 60 - (-48) = 108; r32 = 60 - 56 = 4; r42 = 60 - 60 = 0; 3. Рассчитываем 3-й столбец матрицы рисков. r13 = 80 - 30 = 50; r23 = 80 - 20 = 60; r33 = 80 - (-24) = 104; r43 = 80 - 80 = 0;
Результаты вычислений оформим в виде таблицы.
Выбираем из (50; 108; 104; 32) минимальный элемент min=32 Вывод: выбираем стратегию N=4. Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A4. |
