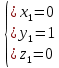Системой линейных алгебраических уравнений (СЛАУ) с n неизвестными называется система вида:
 (1) (1)
где  – неизвестные, – неизвестные,  – коэффициенты при неизвестных и – коэффициенты при неизвестных и  – свободные члены системы уравнений. – свободные члены системы уравнений.
Во все уравнения неизвестные входят в первой степени, поэтому уравнения называются линейными. Каждый коэффициент  системы имеет два индекса, первый iуказывает номер уравнения, а второй j – номер неизвестного, при котором находится данный коэффициент. В рассматриваемой системе (1) будем считать, что коэффициенты являются постоянными числами. системы имеет два индекса, первый iуказывает номер уравнения, а второй j – номер неизвестного, при котором находится данный коэффициент. В рассматриваемой системе (1) будем считать, что коэффициенты являются постоянными числами.
Свободные члены  могут принимать различные значения. могут принимать различные значения.
Система линейных алгебраических уравнений (1) называется однородной, если все ее свободные члены равны нулю
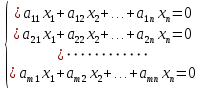 (2) (2)
Если не все свободные члены системы раны нулю, то система называется неоднородной.
Пример 1. Система линейных уравнений с двумя неизвестными:
 (3) (3)
является неоднородной.
Система линейных уравнений (1) состоит из m уравнений сn неизвестными. В зависимости от количества уравнений и неизвестных система (1) может быть квадратной или неквадратной.
Система линейных алгебраических уравнений (1) называется квадратной, если количество ее уравнений и неизвестных равны, то есть 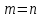 . .
Например, система, рассмотренная в примере 1, является квадратной.
Пример 2. Система линейных уравнений с двумя неизвестными:
 (4) (4)
не является квадратной, так как число уравнений  , а число неизвестных , а число неизвестных  , то есть , то есть 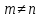 . .
Решением системы линейных алгебраических уравнений (1) называется упорядоченный набор  чисел чисел  , при подстановке которых в систему (1), вместо соответствующих неизвестных, каждое уравнение системы обращается в верное равенство. , при подстановке которых в систему (1), вместо соответствующих неизвестных, каждое уравнение системы обращается в верное равенство.
Пример 3. Найти решение система линейных уравнений:

Решение. Данная система имеет единственное решение 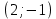 . В этой совокупности чисел предпологается, что . В этой совокупности чисел предпологается, что
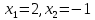 . .
При подстановке этих значений неизвестных в уравнения системы, выполняются все равенства:

Замечание. Решение является упорядоченной парой чисел. Если в паре 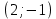 числа поменять местами, то полученная пара числа поменять местами, то полученная пара  уже не удовлетворяет систему уравнений: уже не удовлетворяет систему уравнений:

то есть 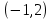 не является решением данной системы. не является решением данной системы.
Не всякая система имеет решение.
Система линейных алгебраических уравнений (1) называется совместной, если она имеет хотя бы одно решение.
Если система не имеет ни одного решения, то она называется несовместной.
Например, система (3) имеет единственное решение 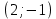 и является совместной, а система (4) не имеет ни одного решения и является несовместной. и является совместной, а система (4) не имеет ни одного решения и является несовместной.
Пример 4. Проверить на совместность систему линейных уравнений:
 (5) (5)
Решение. Данная система имеет бесконечное множество решении вида 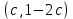 , где , где  – произвольное число. Действительно, при подстановке в систему получим следующие равенства: – произвольное число. Действительно, при подстановке в систему получим следующие равенства:

Следовательно, рассматриваемая система имеет бесконечное множество решении и является совместной.
Из приведенных примеров видим, что совместная система может иметь лишь одно решение или бесконечное множество решений.
Если совместная система линейных алгебраических уравнений (1) имеет только одно решение, то она называется определенной.
Если совместная система имеет более одного решения, то она называется неопределенной.
Например, система (3) – определенная, так как имеет единственное решение 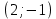 , а система (5) – неопределенной, так как она имеет бесконечное множество решении. При этом решение , а система (5) – неопределенной, так как она имеет бесконечное множество решении. При этом решение 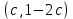 или или
 , ,
при произвольном числе  , называется общим решением системы, а при конкретном значении , называется общим решением системы, а при конкретном значении  , например , например  , решение , решение

называется частным решением рассматриваемой системы.
При рассмотрении системы линейных алгебраических уравнений главная задача – решить данную систему, то есть
определить совместность или несовместность системы;
если система совместна, то найти общее решение.
Для решения системы линейных алгебраических уравнений (1) очень удобно рассматривать систему в матричной форме.
Матричной формой системы линейных алгебраических уравнений (1) называется представление системы в виде
 , (6) , (6)
где
 , ,
матрица размерности  , составленная из коэффициентов , составленная из коэффициентов  при неизвестных; при неизвестных;

матрица размерности  , составленная из неизвестных; , составленная из неизвестных;

матрица размерности 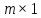 , составленная из свободных членов системы. , составленная из свободных членов системы.
Замечание.
При составлении матричной формы системы должны строго соблюдаться правила умножения матриц.
Матрица  , составленная из коэффициентов , составленная из коэффициентов  при неизвестных, называется основной матрицей. при неизвестных, называется основной матрицей.
Пример 5. Записать систему (3)

в матричной форме.
Решение. Составим матрицы данной системы:
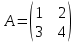 , ,  , ,  . .
Тогда матричная форма системы (3) запишется в следующим виде:

Пример 6. Записать систему (4)

в матричной форме.
Решение. Составим матрицы данной системы:
 , ,  , ,  . .
Тогда матричная форма системы (4) запишется в следующим виде:
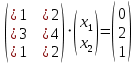
Пример 7. Записать систему (5)

в матричной форме.
Решение. Составим матрицы данной системы:
 , ,  , , 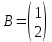 . .
Тогда матричная форма системы (5) запишется в следующим виде:

Матричная форма системы (1) позволяет проводить исследование и решение системы с помощью матриц.
Решение произвольной системы (1) с помощью матричной формы (6) сводится к нахождению ранга основной матрицы и , если система совместна, к построению решении квадратной системы линейных уравнений, образованной базисным минором.
Поэтому, для начала, рассмотрим случай, когда основная матрица  системы является квадратной матрицей системы является квадратной матрицей  -го порядка. -го порядка.
Система линейных алгебраических уравнений (1) называется невырожденной, если
система квадратная;
основная матрица системы является невырожденной, то есть 
Система линейных алгебраических уравнений (1) называется вырожденной, если
система квадратная;
основная матрица системы является вырожденной, то есть  . .
Пример 8. Исследовать на вырожденность систему (3):

Решение. Составим основную матрицы данной системы:
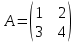 , ,
и вычислим ее определитель:

Следовательно, система является невырожденной.
Пример 9. Исследовать на вырожденность систему (5):

Решение. Составим основную матрицы данной системы:

и вычислим ее определитель:

Система вырожденная.
Методы решения невырожденных систем линейных алгебраических уравнений. Невырожденные системы уравнений можно решить матричным методом, методом Крамера и методом элементарных преобразовании Гаусса.
Метод Гаусса является универсальным методом, который можно использовать как для невырожденных, так и для вырожденных систем линейных уравнений.
Матричный метод решения системы линейных уравнений.
Рассмотрим невырожденную систему линейных алгебраических уравнений (1) в матричной форме (6):
 . .
Следовательно,  и существует обратная матрица и существует обратная матрица  . .
Теорема 1. Невырожденная система линейных алгебраических уравнений имеет единственное решение, которое находится по формуле:
 . (7) . (7)
Следствие. Невырожденная система линейных алгебраических уравнений является совместной и определенной системой.
Правило нахождения решений невырожденной системы матричным методом:
найти обратную матрицу по формуле

где  – присоединенная матриц;. – присоединенная матриц;.
обе части матричного уравнения (6) системы умножить слева на обратную матрицу  и найти решение по формуле: и найти решение по формуле:
 . .
Пример 10. Используя матричный метод найти решение системы (3):

Решение. Составим матрицы данной системы:
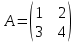 , ,  , ,  . .
Тогда матричная форма системы (3) запишется в следующим виде:

Данная система является невырожденной и определитель ее основной матрицы отличен от нуля и равен:

Как было показано в примере 15 из темы №1, обратная матрица имеет вид:

Тогда решение системы найдем по формуле (7):
 , ,
то есть 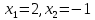 . Данный результат полностью подтверждает верность решения примера 3. . Данный результат полностью подтверждает верность решения примера 3.
Решение невырожденной системы алгебраических уравнений можно построить другим способом, который называется правилом Крамера.
Правило Крамера
Теорема 2. Пусть система линейных алгебраических уравнений является
квадратной, с основной матрицей  -го порядка -го порядка  ; ;
невырожденной, то есть  ; ;
 – определитель матрицы, полученной из основной матрицы – определитель матрицы, полученной из основной матрицы  системы, заменой i-го столбца столбцом свободных членов системы. системы, заменой i-го столбца столбцом свободных членов системы.
Тогда данная невырожденная система линейных алгебраических уравнений имеет единственное решение, которое находится по формуле:
 , ,  . (8) . (8)
Эти формулы называются формулами Крамера.
Правило решения системы линейных алгебраических уравнений с помощью формулы Крамера:
построить основную матрицу данной системы;
вычислить определитель основной матрицы системы;
если определитель основной матрицы системы отличен от нуля,  , то вычислить определители , то вычислить определители  , ,  , и найти неизвестные переменные , и найти неизвестные переменные  по формуле Крамера: по формуле Крамера:
 , ,  . .
если определитель основной матрицы системы равен нулю,  , то необходимо исследовать систему на совместность. , то необходимо исследовать систему на совместность.
Пример 11. Найти решение системы (3) по правилу Крамера:

Решение. 1) Построим основную матрицу системы:
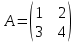 . .
2) Вычислим определитель основной матрицы:

3) Найдем дополнительные определители:

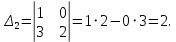
4) Вычислим неизвестные переменные  по формуле Крамера: по формуле Крамера:
 
Замечание. Матричный метод и правило Крамера обладают двумя существенными недостатками:
Они применимы только для систем с невырожденной квадратной матрицей и не работают в случае, когда  . .
С ростом порядка  основной матрицы объём вычислений для этих методов очень быстро возрастает и для основной матрицы объём вычислений для этих методов очень быстро возрастает и для  они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать более универсальный метод Гаусса. они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать более универсальный метод Гаусса.
Эти недостатки никак не умоляют значимость этих методов. Любые произвольные системы линейных уравнений, после нахождения базисного минора, сводятся к решению невырожденных систем.
Вопрос 2. Метод Гаусса решения произвольных систем линейных уравнений.
Метод Гаусса является универсальным методом и применим для любой системы линейных уравнений. Он основан на элементарных преобразованиях матрицы данной системы уравнений и позволяет определить совместность или несовместность системы и найти ее решения.
Пусть задана произвольная система линейных алгебраических уравнений (1), состоящая из  линейных уравнений с линейных уравнений с  неизвестными. Для системы (1) сотавим ее основную матрицу неизвестными. Для системы (1) сотавим ее основную матрицу  , из коэффициентов , из коэффициентов  при неизвестных при неизвестных  , ,
 , ,
расширенную матицу  , полученную присоедрнением к матрице , полученную присоедрнением к матрице  стобца из свободных членов, стобца из свободных членов,

Элементарными преобразованиями матрицы  называются следующие действия: называются следующие действия:
1) Перестановка строк или столбцов местами.
2) Умножение строки или столбца на ненулевой коэффициент.
3) Прибавление к одной строке или столбцу матрицы другой её строки или столбца, умноженной на некоторое число  . .
4) Зачёркивание нулевой строки или столбца матрицы.
Методом Гаусса решения произвольной системы линейных алгебраических уравнений (1) называется приведение расширенной матрицы  этой системы к ступенчатому виду, с помощью элементарных преобразовании ее строк, и последовательное определение неизвестных из этой ступенчатой системы. этой системы к ступенчатому виду, с помощью элементарных преобразовании ее строк, и последовательное определение неизвестных из этой ступенчатой системы.
Метод Гаусса состоит из двух частей:
прямой ход – приведение системы к ступенчатому виду;
обратный ход – определение неизвестных из полученной ступенчатой системы.
Замечание. В отличие от процесса определения ранга матрицы, в методе Гаусса элементарные преобразования матрицы проводятся над ее строками.
Пример 16. Исследовать и решить систему
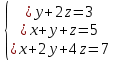
Решение. 1) В первом уравнении отсутствует неизвестная 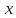 . Это означает, что ее коэффициент равен нулю, то есть система в полном виде записывается следующим образом: . Это означает, что ее коэффициент равен нулю, то есть система в полном виде записывается следующим образом:

Запишем расширенную матрицу  : :
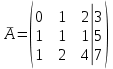
2) Первую строку переставляем со второй
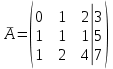 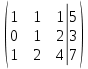
3) К третьей строке преобразованной матрицы прибавим первую строку, умноженную на (-1):
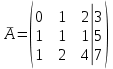
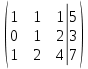
 . .
4) К третьей строке преобразованной матрицы прибавим вторую, умноженную на (-1):
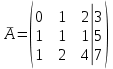
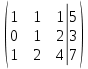

 . .
5) Расширенная матрица приведена к ступенчатому виду. Противоречивых записей нет. Ранг матрицы равен количеству неизвестных:  . Следовательно, система совместная и определенная, имеет единственное решение. . Следовательно, система совместная и определенная, имеет единственное решение.
6) Перепишем исходную систему уравнений с помощью полученной ступенчатой матрицы:
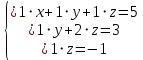
7) Начиная с последнего уравнения, последовательно находим значения неизвестных:
  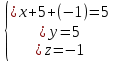 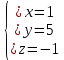
Это единственное решение системы.
Пример 17. Исследовать и решить систему

Решение. 1) Запишем расширенную матрицу  : :

2) Первую строку переставляем со второй

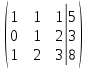
3) К третьей строке преобразованной матрицы прибавим первую строку, умноженную на (-1):

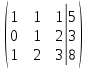

4) К третьей строке преобразованной матрицы прибавим вторую, умноженную на (-1):

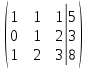

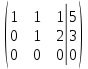
5) Расширенная матрица приведена к ступенчатому виду. Противоречивых записей нет. Система совместна. Ранг матрицы равен  ,количество неизвестных ,количество неизвестных  , то есть , то есть  . Следовательно, система совместная и неопределенная, имеет бесконечное множество решений. . Следовательно, система совместная и неопределенная, имеет бесконечное множество решений.
6) Перепишем исходную систему уравнений с помощью полученной ступенчатой матрицы, отбросив нулевую строку:

7) Количество базисных неизвестных равно рангу  . В данном примере, базисные неизвестные: . В данном примере, базисные неизвестные:  . Свободная неизвестная: . Свободная неизвестная:  . Перенесем свободную неизвестную на правую часть уравнений: . Перенесем свободную неизвестную на правую часть уравнений:

Придав свободной неизвестной произвольное значение  , начиная с последнего уравнения, последовательно находим значения базисных неизвестных , начиная с последнего уравнения, последовательно находим значения базисных неизвестных  : :
 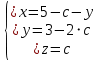 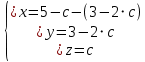 
Это общее решение системы.
Пример 18. Исследовать и решить систему

Решение. 1) Запишем расширенную матрицу  : :
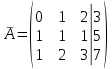
2) Первую строку переставляем со второй
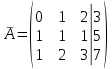

3) К третьей строке преобразованной матрицы прибавим первую строку, умноженную на (-1):
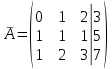


4) К третьей строке преобразованной матрицы прибавим вторую, умноженную на (-1):
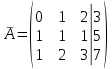



5) В последней строке получили противоречие: 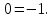
Следовательно, система несовместна.
Пример 19. Исследовать и решить систему

Решение. Данную задачу решим методом Гаусса.
1. Запишем основную матрицу  : :

2. К второй строке прибавим первую строку, умноженную на (-1):


3. К третьей строке прибавим первую строку, умноженную на (-2):



4. К третьей строке прибавим вторую, умноженную на (-1):



 . .
5. Основная матрица приведена к ступенчатому виду. Противоречивых записей нет. Система совместна. Ранг матрицы равен  ,количество неизвестных ,количество неизвестных  , то есть , то есть 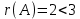 . Следовательно, система неопределенная, имеет бесконечное множество решений. . Следовательно, система неопределенная, имеет бесконечное множество решений.
6. Перепишем исходную систему уравнений с помощью полученной ступенчатой матрицы, отбросив нулевую строку:
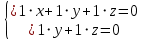
7. Количество базисных неизвестных равно рангу  . В данном примере, базисные неизвестные: . В данном примере, базисные неизвестные:  . Свободная неизвестная: . Свободная неизвестная:  . Перенесем свободную неизвестную на правую часть уравнений: . Перенесем свободную неизвестную на правую часть уравнений:

Придав свободной неизвестной произвольное значение  , начиная с последнего уравнения, последовательно находим значения базисных неизвестных , начиная с последнего уравнения, последовательно находим значения базисных неизвестных  : :
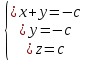   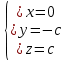
Свойство 5. Однородная система n линейных уравнений с n неизвестными имеет ненулевое решение тогда и только тогда, когда определитель ее основной матрицы равен нулю, то есть  . .
Свойство 6. Если упорядоченный набор чисел  является решение однородной системы линейных уравнений (10), то для произвольного числа является решение однородной системы линейных уравнений (10), то для произвольного числа  набор чисел набор чисел  также решение этой системы. также решение этой системы.
Свойство 7. Сумма любых двух решений однородной системы линейных уравнений (10) также является решением этой системы, то есть если  и и  решение системы (7), то решение системы (7), то

также решение этой системы.
Свойство 8. Любая линейная комбинация решений однородной системы линейных уравнений также является решением этой системы, то есть если  и и  решение системы (7), то для произвольных чисел решение системы (7), то для произвольных чисел 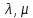 линейная комбинация этих решений линейная комбинация этих решений

также является решением этой системы.
Свойство 9. Сумма любого решения неоднородной системы линейных уравнений с любым решением соответствующей ей однородной системы также является решением неоднородной системы.
Свойство 10. Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей ей однородной системы.
Свойство 11. Общее решение неоднородной системы линейных уравнений равна сумме ее частного решения с общим решением соответствующей ей однородной системы.
Пример 20. Найти общее решение системы

Решение. 1) Исследуем неоднородную систему на совместность. Для этого составим основную и расширенную матрицу
 , , 
Согласно свойству, ранг матрицы не меняется при элементарном преобразовании. Если в расширенной матрице  из четвертого столбца отнять третью (меняется тот столбец с которого вычитают!), то четвертый столбец расширенной матрицы будет равен нулю, а остальные столбцы совпадают со столбцами основной матрицы из четвертого столбца отнять третью (меняется тот столбец с которого вычитают!), то четвертый столбец расширенной матрицы будет равен нулю, а остальные столбцы совпадают со столбцами основной матрицы  . Нулевой столбец на ранг расширенной матрицы не влияет. Следовательно, . Нулевой столбец на ранг расширенной матрицы не влияет. Следовательно, 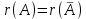 и, по теореме Кронекера-Капелли, рассматриваемая система совместна. и, по теореме Кронекера-Капелли, рассматриваемая система совместна.
Частным решением неоднородной системы является
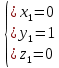
2) Найдем общее решение приведенной системы

3) После элементарных преобразовании система принимает следующий вид (пример 19)



 . .
4) Основная матрица приведена к ступенчатому виду. Противоречивых записей нет. Система совместна. Ранг матрицы равен  ,количество неизвестных ,количество неизвестных  , то есть , то есть 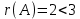 . Следовательно, система неопределенная, имеет бесконечное множество решений. Как показано в примере 19, общее решение этой однородной системы имеет вид: . Следовательно, система неопределенная, имеет бесконечное множество решений. Как показано в примере 19, общее решение этой однородной системы имеет вид:

5) Тогда общее решение неоднородной системы можно определить следующим образом:
  
6) Подставим полученное общее решение в неоднородную систему:
  
Все уравнения системы выполнены одновременно. Следовательно, общее решение найдено правильно.
ДОМАШНЕЕ ЗАДАНИЕ
РЯБУШКО 1 ТОМ
ИДЗ 1.1 (ЗАДАНИЕ 2)
ИДЗ 1.2 (ЗАДАНИЕ 1, 2, 3) |
 Скачать 48.02 Kb.
Скачать 48.02 Kb.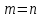 .
. чисел
чисел  , при подстановке которых в систему (1), вместо соответствующих неизвестных, каждое уравнение системы обращается в верное равенство.
, при подстановке которых в систему (1), вместо соответствующих неизвестных, каждое уравнение системы обращается в верное равенство.  , составленная из коэффициентов
, составленная из коэффициентов  при неизвестных, называется основной матрицей.
при неизвестных, называется основной матрицей.
 .
. и найти решение по формуле:
и найти решение по формуле: -го порядка
-го порядка  ;
; ;
; – определитель матрицы, полученной из основной матрицы
– определитель матрицы, полученной из основной матрицы  системы, заменой i-го столбца столбцом свободных членов системы.
системы, заменой i-го столбца столбцом свободных членов системы.  , то вычислить определители
, то вычислить определители  ,
,  , и найти неизвестные переменные
, и найти неизвестные переменные  по формуле Крамера:
по формуле Крамера: , то необходимо исследовать систему на совместность.
, то необходимо исследовать систему на совместность. .
.  основной матрицы объём вычислений для этих методов очень быстро возрастает и для
основной матрицы объём вычислений для этих методов очень быстро возрастает и для  они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать более универсальный метод Гаусса.
они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать более универсальный метод Гаусса. линейных уравнений с
линейных уравнений с  неизвестными. Для системы (1) сотавим ее основную матрицу
неизвестными. Для системы (1) сотавим ее основную матрицу  , из коэффициентов
, из коэффициентов  при неизвестных
при неизвестных  ,
,  называются следующие действия:
называются следующие действия: этой системы к ступенчатому виду, с помощью элементарных преобразовании ее строк, и последовательное определение неизвестных из этой ступенчатой системы.
этой системы к ступенчатому виду, с помощью элементарных преобразовании ее строк, и последовательное определение неизвестных из этой ступенчатой системы.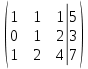
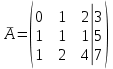
 .
.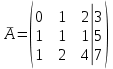

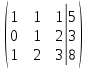





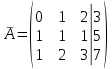

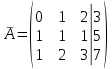







 .
. ,количество неизвестных
,количество неизвестных  , то есть
, то есть 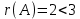 . Следовательно, система неопределенная, имеет бесконечное множество решений. Как показано в примере 19, общее решение этой однородной системы имеет вид:
. Следовательно, система неопределенная, имеет бесконечное множество решений. Как показано в примере 19, общее решение этой однородной системы имеет вид:







 (1)
(1) – неизвестные,
– неизвестные,  – коэффициенты при неизвестных и
– коэффициенты при неизвестных и  – свободные члены системы уравнений.
– свободные члены системы уравнений. 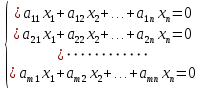 (2)
(2) (3)
(3) (4)
(4) , а число неизвестных
, а число неизвестных  , то есть
, то есть 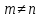 .
.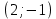 . В этой совокупности чисел предпологается, что
. В этой совокупности чисел предпологается, что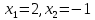 .
.
 уже не удовлетворяет систему уравнений:
уже не удовлетворяет систему уравнений:
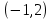 не является решением данной системы.
не является решением данной системы. (5)
(5)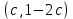 , где
, где  – произвольное число. Действительно, при подстановке в систему получим следующие равенства:
– произвольное число. Действительно, при подстановке в систему получим следующие равенства:
 ,
, , решение
, решение
 , (6)
, (6) ,
,  , составленная из коэффициентов
, составленная из коэффициентов 
 , составленная из неизвестных;
, составленная из неизвестных;
 , составленная из свободных членов системы.
, составленная из свободных членов системы.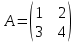 ,
,  ,
,  .
.
 ,
,  .
.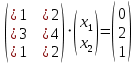
 ,
, 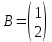 .
.


 . (7)
. (7)
 – присоединенная матриц;.
– присоединенная матриц;.

 ,
, ,
, 
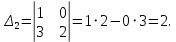



 .
.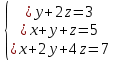
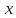 . Это означает, что ее коэффициент равен нулю, то есть система в полном виде записывается следующим образом:
. Это означает, что ее коэффициент равен нулю, то есть система в полном виде записывается следующим образом:
 .
. . Следовательно, система совместная и определенная, имеет единственное решение.
. Следовательно, система совместная и определенная, имеет единственное решение. 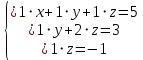


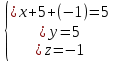
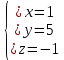

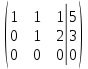
 ,количество неизвестных
,количество неизвестных  . Следовательно, система совместная и неопределенная, имеет бесконечное множество решений.
. Следовательно, система совместная и неопределенная, имеет бесконечное множество решений. 
 . Свободная неизвестная:
. Свободная неизвестная:  . Перенесем свободную неизвестную на правую часть уравнений:
. Перенесем свободную неизвестную на правую часть уравнений:
 , начиная с последнего уравнения, последовательно находим значения базисных неизвестных
, начиная с последнего уравнения, последовательно находим значения базисных неизвестных 
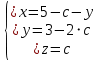
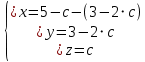



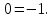

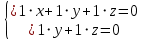
 . В данном примере, базисные неизвестные:
. В данном примере, базисные неизвестные: 
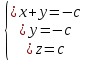


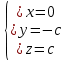
 .
. является решение однородной системы линейных уравнений (10), то для произвольного числа
является решение однородной системы линейных уравнений (10), то для произвольного числа  набор чисел
набор чисел  также решение этой системы.
также решение этой системы. и
и  решение системы (7), то
решение системы (7), то 
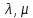 линейная комбинация этих решений
линейная комбинация этих решений

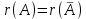 и, по теореме Кронекера-Капелли, рассматриваемая система совместна.
и, по теореме Кронекера-Капелли, рассматриваемая система совместна.