Итоговая по математике. ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА. Задача Найти матрицу, обратную матрице. Решение. Найдем а 1 Вычислим определитель матрицы
 Скачать 64.68 Kb. Скачать 64.68 Kb.
|
|
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА Задача 1. Найти матрицу, обратную матрице 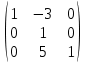 . .Решение. Найдем А-1 Вычислим определитель матрицы: 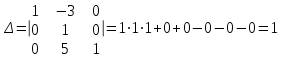 Вычислим алгебраические дополнения: А11 = 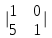 = 1; А21 = – = 1; А21 = – 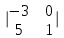 = 3; А31 = = 3; А31 = 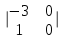 = 0; А12 = – = 0; А12 = – 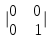 = 0; = 0; А22 = 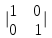 = 1; А32 = – = 1; А32 = – 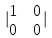 = 0; А13 = = 0; А13 = 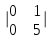 = 0; А23 = – = 0; А23 = – 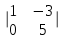 = – 5; = – 5; А33 = 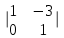 = 1. = 1.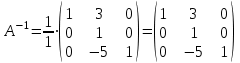 Ответ. 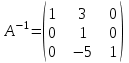 Задача 2. Решить СЛАУ 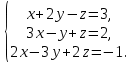 Решение. Проверим систему на совместимость. Составим расширенную матрицу системы и приведем эту матрицу к треугольному виду путем элементарных преобразований 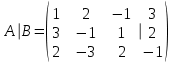 . . Первую строку прибавим ко второй строке, умножив на (-3): 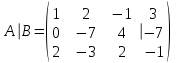 Первую строку, умножив на (-2), прибавим к третьей строке: 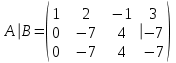 Вторую строку, умножив на (-1), прибавим к третьей строке: 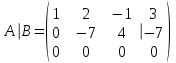 . .Нулевую строку вычеркиваем. Преобразованная матрица имеет треугольный вид, причем ранг матрицы А равен рангу расширенной матрицы  ( (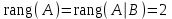 ). ). Следовательно, согласно теореме Кронекера-Капелли, система совместна. Система имеет бесконечное множество решений, так как ранг меньше числа неизвестных. Получаем равносильную систему: 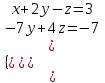 Пусть z = U. Тогда: 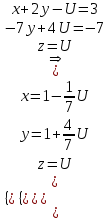 Ответ: 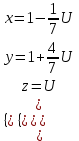 Задача 3. Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен: а) ровно 6-ти изделиям; б) более чем 7-ми изделиям; в) хотя бы одному изделию; г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность. Решение. n = 9, p = 0,2, q = 1 – 0,2 = 0,8 По формуле Бернулли 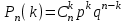 находим искомые вероятности: находим искомые вероятности:а) ровно 6-ти изделиям, k = 6 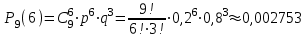 б) более чем 7-ми изделиям 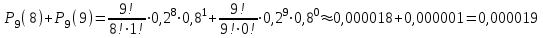 в) хотя бы одному изделию 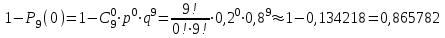 г) укажем наивероятнейшее число изделий, получивших знак высшего качества, и найдем соответствующую ему вероятность. Наивероятнейшее число k0 определяют из двойного неравенства 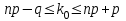 . .Получим 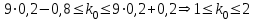 . .Двойному неравенству удовлетворяют два числа, следовательно существуют два наивероятнейших числа 1 и 2. 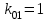 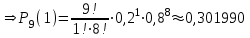 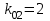 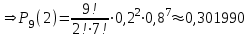 Ответ. а) 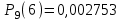 б) 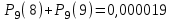 в) 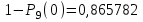 г) 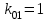 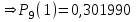 , , 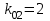 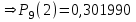 |
