конспект урока. Конспект урока по геометрии на тему _Скалярное произведение вект. Скалярное произведение векторов. Решение задач (урок 5)
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
5. ПЛАН-КОНСПЕКТ УРОКА МАТЕМАТИКИ Тип урока: урок ознакомления с новым материалом. Тема: «Скалярное произведение векторов. Решение задач» (урок № 5) Цели: образовательные: ввести понятие угла между векторами, ввести понятие «скалярное произведение векторов», его свойств и формировать умение применять скалярное произведение векторов при решении геометрических задач; развивающие: способствовать формированию умения определять угол между векторами, научить применять формулу для нахождения скалярного произведения векторов, способствовать развитию математического кругозора и логического мышления; воспитательные: содействовать воспитанию интереса к теме «векторы», воспитывать чувство коллективизма, самоконтроля, ответственности. Оборудование: тетрадь, учебник (Атанасян Л.С.), ручка, карандаш, линейка, доска, мел и цветные мелки, проектор и презентация «скалярное произведение векторов». Структура урока Организационный момент (1 мин). Проверка домашнего задания (5 мин). Мотивация учебной деятельности. (1 мин). Подготовительный этап (4 мин). Объяснение нового материала (17 мин). Физкультминутка (1 мин) Закрепление (11 мин). Подведение итогов урока (4 мин). Рефлексия (1 мин). Постановка домашнего задания (1 мин). ХОД УРОКА 1. Организационный момент Учитель приветствует учащихся, проверяет их готовность к уроку и отмечает в журнале отсутствующих. 2. Проверка домашнего задания Тема предыдущего урока: «Соотношения между сторонами и углами треугольника. (Теорема синусов. Теорема косинусов)» Домашнее задание, заданное учащимся на предыдущем уроке: прочитать § 2, выучить теорему о площади треугольника, теорему синусов и теорему косинусов, уметь отвечать на вопросы 7-12 на с. 271. Решить задачи № 1020 (в), № 1025 (б, и), № 1029, № 1031 (б). Решения задач из домашнего задания. № 1020 (в) Найдите площадь треугольника  , если , если  см, см, 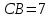 см, см,  . .Решение:  см2. см2.№ 1025 (б, и) С помощью теорем синусов и косинусов решите треугольник  , если: , если:б)  , , 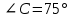 , ,  ; ;и)  , ,  , ,  . .Решение: Б)  . .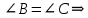 треугольник равнобедренный и треугольник равнобедренный и  . .По теореме синусов:  ; ; , , 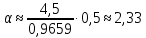 . .И) Применим теорему косинусов:  ; ; ; ; ; ;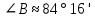 . . ; ; ; ; ; ;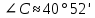 . . . .№ 1029 Найдите биссектрисы треугольника, если одна из его сторон равна 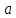 , а прилежащие к этой стороне углы равны , а прилежащие к этой стороне углы равны  и и 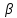 . .Р 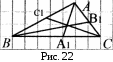 ешение: ешение: Дано:  , ,  , ,  , , . .Найти: 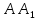 , ,  , , 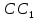 . .Рассмотрим  . .По теореме синусов:  ; ;  ; ;  . .Рассмотрим  . .По теореме синусов:  ; ;  ; ;  . .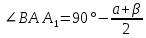 . .Рассмотрим  . .По теореме синусов: 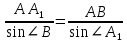 ; ;  ; ;  . .№ 1031 (б) Выяснить, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны 17, 8 и 15. Решение:  , ,  , ,  . .По теореме косинусов:  ; ;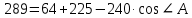 ; ; ; ; ; ; – прямоугольный. – прямоугольный.Домашнее задание проверяется в комбинированной форме «взаимная проверка во время сверки с проектором». Ученики обмениваются тетрадями с соседом по парте. Правильный вариант выполнения домашнего задания выводится учителем на экран проектора. Ученики сверяются с ним, исправляют допущенные ошибки своего соседа. Ставят оценку и объясняют какие ошибки были допущены. Обсуждаются спорные вопросы с учителем и всем классом. После этого доску делят на 3 половины (количество рядов в классе), на каждой половине выписывают оценки учеников за домашнее задание соответствующего ряда (если домашнее задание отсутствует у какого-то ученика, то вместо оценки ставится 0). Потом каждый из рядов вычисляет среднюю оценку своего ряда и эти средние балы сравниваются. Таким образом, класс делает вывод, какой из рядов лучше выполнил домашнее задание. Такая форма оценивания позволяет смотивировать учеников более старательнее выполнять (и вообще выполнять) домашнее задание, вырабатывает коллективный дух (более успевающие будут помогать неуспевающим при выполнении задания, тем самым не подозревая, что подтягивают отстающих), мотив соперничества, стремление к лучшему. 3. Мотивация учебной деятельности Начать урок хотелось бы словами американского физика Юджина Пола Вигнера: «Математика – это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями». Сегодня как раз мы и будем заниматься такими хитроумными операциями над специально разработанными понятиями. А полученные знания нам пригодятся в дальнейшем. Шарада: Мой первый слог – почтенный срок, Коль прожит он недаром; Модель второго на столе, Румяна, с пылу с жару. Меня вы встретите везде – Такой я вездесущий. А имя громкое мое – Латинское «несущий». (Век-тор) Тема нашего сегодняшнего урока «Скалярное произведение векторов». Дети записывают тему в тетрадь. Итак, сегодня на уроке мы узнаем, что такое угол между векторами и скалярное произведение векторов; научимся находить скалярное произведение, если известны координаты векторов; познакомимся со свойствами скалярного произведения. Но, прежде чем, перейти к новой теме, мы должны привести в систему и наши знания по ранее изученным темам геометрии. 4. Подготовительный этап Повторим то, что вы уже знаете. Табличные значения косинуса и синуса углов  , ,  , ,  . .Что такое вектор? (Отрезок, который имеет направление) Чем характеризуется отрезок? (Направлением и длиной) По какой формуле вычисляется длина вектора? (  ) )Какие координаты имеет нулевой вектор? (  ) )Могут ли нулевые координаты быть у ненулевого вектора? (У ненулевого вектора может быть только одна из координат нулевая) Посмотрите на рисунок и скажите, какие векторы коллинеарные (  ), какие неколлинеарные ( ), какие неколлинеарные ( ), какие векторы соноправленные ( ), какие векторы соноправленные ( и и  , ,  и и  ), какие противоположно направленные ( ), какие противоположно направленные (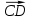 и и 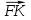 , , 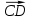 и и  , , 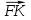 и и  , ,  и и )? )? Рис. 23 Какие действия вы умеете уже выполнять над векторами? (Сложение, вычитание и умножение на число) Что получается в результате этих операций? (Вектор) Какую операцию вы ещё не рассматривали? (Умножение вектора на вектор) Сегодня мы и займёмся произведением векторов. 5. Объяснение нового материала Прежде чем определить скалярное произведение векторов, давайте построим угол между векторами. Пусть нам даны два ненулевых вектора  и и  . Отложим от произвольной точки . Отложим от произвольной точки  векторы векторы 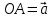 и и  (рис. 24). Если эти векторы не являются сонаправлеными, то угол между (рис. 24). Если эти векторы не являются сонаправлеными, то угол между  и и  образуют угол образуют угол  и градусную меру этого угла обозначим через и градусную меру этого угла обозначим через  и будем говорить, что угол между векторами и будем говорить, что угол между векторами  и и  равен равен  , принято, что , принято, что  . .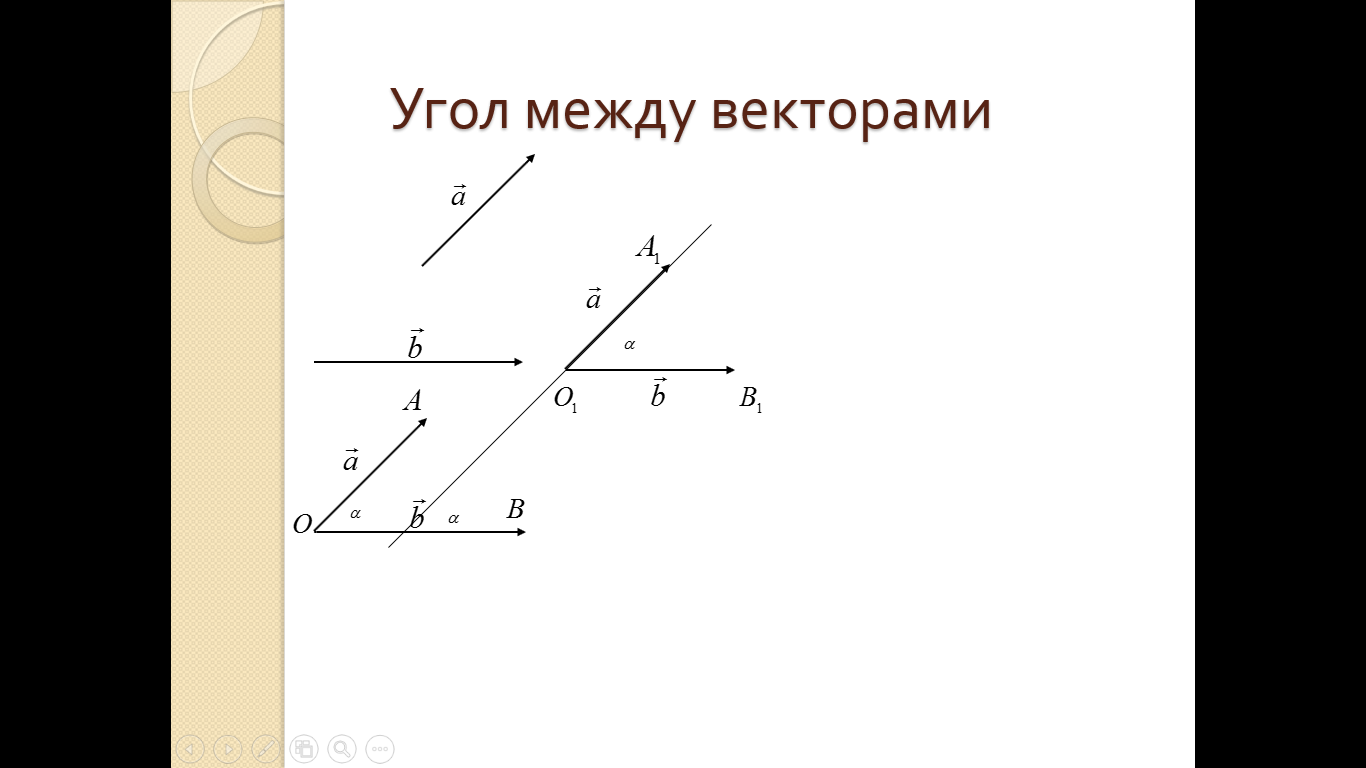 Рис. 24 Таким образом, углом между любыми двумя ненулевыми векторами  и и  называется угол между равными им векторами с общим началом. Обратите внимание, что угол называется угол между равными им векторами с общим началом. Обратите внимание, что угол  не зависит от выбора точки не зависит от выбора точки  от которой откладываются вектора. от которой откладываются вектора.Если же вектора параллельны или один из них равен нулю, то угол  по определению. по определению. Угол между векторами  и и  обозначается так: обозначается так:  . .Рассмотрим примеры (рис. 25).  Рис. 25 Два вектора называются перпендикулярными, если угол между ними равен  . .Скажите, глядя на рисунок, какие вектора будут перпендикулярными? (  и и  , ,  и и  , ,  и и  ) )Теперь, зная, как определить угол между векторами, мы можем определить скалярное произведение векторов. Скалярным произведением векторов называется произведение их длин на косинус угла между ними: 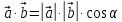 Запишите формулу в тетрадь и обведите в рамку. Таким образом, чтобы найти скалярное произведение нужно знать длины векторов и угол между ними. Решим пример. Дано: 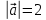 , ,  , ,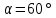 . .Найти: 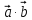  = = ; ;  . .Обратите внимание, что в результате скалярного произведение обязательно будет число. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Если  (сонаправлены), то получаем (сонаправлены), то получаем  . В частности, . В частности, 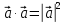 . Скалярное произведение . Скалярное произведение  называется скалярным квадратом вектора называется скалярным квадратом вектора  и обозначается и обозначается  . Таким образом, скалярный квадрат вектора равен квадрату его длины. . Таким образом, скалярный квадрат вектора равен квадрату его длины.Скалярное произведение двух векторов можно вычислить, зная координаты векторов. Запишем теорему. Теорема. В прямоугольной системе координат скалярное произведение векторов  и и  выражается формулой выражается формулой 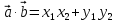 . .Доказательство рассмотрите дома самостоятельно. Давайте теперь посмотрим какими свойствами обладает скалярное произведение. Из теоремы следует два утверждения. Следствие 1: Ненулевые векторы  и и  перпендикулярны тогда и только тогда, когда перпендикулярны тогда и только тогда, когда  . .Следствие 2: Косинус угла  между ненулевыми векторами векторов между ненулевыми векторами векторов  и и  выражается формулой выражается формулой 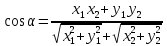 . .Давайте теперь посмотрим какими свойствами обладает скалярное произведение. Запишите подзаголовок: свойства скалярного произведения. Для любых векторов  , ,  , ,  и любого числа и любого числа  справедливы соотношения: справедливы соотношения: 1о.  , причем , причем  при при  . . 2о.  (переместительный закон). (переместительный закон). 3о.  (распределительный закон). (распределительный закон). 4о. 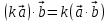 (сочетательный закон). (сочетательный закон).Давайте докажем с вами эти свойства. Свойство 1о непосредственно следует из формулы 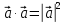 , а свойство 2о – из определения скалярного произведения. , а свойство 2о – из определения скалярного произведения.Докажем свойства 3о и 4о. Введём прямоугольную систему координат и обозначим координаты векторов  , ,  , ,  так: так:  , ,  , ,  . .Используя формулу скалярного произведения в координатах, получаем  . .Свойство 3о доказано. Докажем теперь свойство 4о. Вектор  имеет координаты имеет координаты  , поэтому , поэтому  . .6. Физкультминутка Учащиеся выполняют за учителем. Упражнение 1. Сжать пальцы в кулак и сделать круговые движения кистью влево, затем вправо. Упражнение 2. С силой сжимать и разжимать пальцы, пока они не устанут. Упражнение 3. Выпрямить пальцы, большой палец отвести в сторону и проделать им круговые движения сначала влево, затем вправо. Также и упражнения для глаз.  Рис. 26 7. Закрепление Теперь давайте выполним с вами задания. № 1039. Диагонали квадрата  пересекаются в точке пересекаются в точке  . Найдите угол между векторами: а) . Найдите угол между векторами: а) и и  ; б) ; б) и и  ; в) ; в) и и  ; г) ; г) и и  . .Выполняют у доски (а) и (б) с пояснением, (в) и (г) выполняют самостоятельно в тетради. № 1041 (а, б). Вычислите скалярное произведение векторов  и и  , если , если 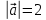 , ,  , а угол между ними равен: а) , а угол между ними равен: а)  ; б) ; б)  . .Какую формулу будем использовать? А) выполняют у доски, а б) самостоятельно в тетради. № 1044 (а, б). Вычислите скалярное произведение векторов  и и  , если: а) , если: а)  и и  ; б) ; б)  и и  . . Как будем находить? (а) выполняют у доски, а (б) самостоятельно в тетради. № 1048. Найдите косинусы углов треугольника с вершинами  , ,  и и  . .По какой формуле будем вычислять? Выполняют у доски. 8. Подведение итогов Учитель предлагает вспомнить цель и задачи урока. Ответить на вопрос: «Достигнута ли цель урока?» Сегодня на занятии мы вспомнили понятие вектора, виды векторов, а также познакомились со скалярным произведением, с их свойствами, научились решать простейшие задачи на данную тему. Я думаю, что у вас сложилось более полное представление о векторах. И у меня появилась уверенность, что с решением простейших задач на данную тему вы справитесь. Фронтальным опросом вместе с учащимися подводятся итоги занятия: Какие операции теперь мы можем выполнять над векторами? (Сложение, вычитание, умножение на число и скалярное произведение векторов) Скажите, что нужно знать для нахождения скалярного произведения? (Длины векторов и угол между ними) Чем отличаемся изученное действие от предыдущих? (В результате получается всегда число) А если векторы заданы в координатах, мы можем найти скалярное произведение? (Да, по формуле, данной в теореме) 9. Рефлексия Учитель раздаёт всем учащимся карточки-анкеты под названием «Насытились?», которые в совокупности объединяются в книгу жалоб и пожеланий ресторана «Скалярное произведение векторов», посетителями которого только что были учащиеся. Ученикам предлагается поделиться своими ощущениями. «Насытились?» Я съел бы еще этого … ________________________________________________________________________________________________________________________________________ Больше всего мне понравилось … ________________________________________________________________________________________________________________________________________ Я почти переварил … ________________________________________________________________________________________________________________________________________ Этот ресторан … ____________________________________________________________________ ____________________________________________________________________ Я переел … ____________________________________________________________________ ____________________________________________________________________ Пожалуйста, добавьте … ________________________________________________________________________________________________________________________________________В ваш ресторан я приду ещё раз, потому что … ________________________________________________________________________________________________________________________________________ 10. Постановка домашнего задания Учащиеся записывают домашнее задание: прочитать по учебнику §3, выучить определения угла между векторами, скалярного произведения векторов, теорему о скалярном произведении в координатах, свойства скалярного произведения. Решить задачи: № 1039 (ж, з). Диагонали квадрата  пересекаются в точке пересекаются в точке  . Найдите угол между векторами: ж) . Найдите угол между векторами: ж) и и  ; з) ; з) и и  . .№ 1041 (в). Вычислите скалярное произведение векторов  и и  , если , если 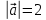 , ,  , а угол между ними равен , а угол между ними равен  . .№ 1044 (в). Вычислите скалярное произведение векторов  и и  , если , если  и и  . .№ 1047 (а, б). При каком значении  векторы векторы  и и  перпендикулярны, если: а) перпендикулярны, если: а) 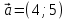 и и  ; б) ; б)  и и 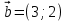 . .№ 1049. Найдите углы треугольника с вершинами  , ,  и и  . .Спасибо за урок! Тема урока: Скалярное произведение векторов. Цели урока: Познакомить учащихся с понятием угла между векторами; ввести понятие скалярного произведения двух векторов, скалярного квадрата вектора; рассказать о применении скалярного произведения векторов в физике, механике; показать применение скалярного произведения векторов при решении задач; развивать логическое мышление учащихся. Тип урока: Изучение нового материала Оборудование: компьютер, презентация, таблицы. Ход урока: Организационный момент Учитель приветствует детей. Ставит цель урока. Актуализация знаний Математический диктант ( презентация – слайд 3) ( учащиеся выполняют работу и с помощью ключа оценивают свою деятельность) Дано: АВСD – параллелограмм Найти: 1) векторы, коллинеарные вектору ОС; 2) векторы, сонаправленные вектору АВ; 3) векторы, противоположно направленные вектору ВС; 4) векторы, равные вектору ВО; 5) ВD, если АВ = 4, АД = 5, < ВАD = 600; Изучение нового материала (презентация – слайд4) Обозначение угла между векторами Слайд 5 (Возьмите на заметку) Два вектора называются перпендикулярными, если угол между ними равен 900. Слайд 6 (Ответьте на вопросы) Повторить по настольным таблицам сложение и вычитание векторов, умножение вектора на число. Введём ещё одно действие над векторами – скалярное умножение векторов. В отличии от суммы и разности векторов скалярное произведение есть число (скаляр) –именно это и обусловило название операции. Слайд 7 (определение скалярного произведения) Учащиеся делают записи в тетради Слайд 8 Закрепление изученного материала Решение задач по учебнику № 1041(а) –у доски (б) – I вар. (в) – II вар. 2) № 1039(а,б,ж,з) по готовым чертежам ( на партах листочки с чертежами) №1040 (а, д, е) Сайд 9 ( Применение скалярного произведения векторов в физике) 3) Выполнение тестовых заданий Слайд (10, 11,12) 5) Итог урока 6) Дом.задание п.101,102 повт.п.87 № 1039(в,г), 1040(г), 1042(а,б) |
