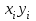Контрольная. Эконометрика МУ им. Витте РР Вариант 12 (копия). Содержание Задание 2 Выполнение Задания 3 Построение линейной модели парной регрессии 3 Расчет коэффициента корреляции 5 Расчет коэффициента эластичности 6 Прогноз

Название	Содержание Задание 2 Выполнение Задания 3 Построение линейной модели парной регрессии 3 Расчет коэффициента корреляции 5 Расчет коэффициента эластичности 6 Прогноз
Анкор	Контрольная
Дата	13.09.2022
Размер	57 Kb.
Формат файла
Имя файла	Эконометрика МУ им. Витте РР Вариант 12 (копия).docx
Тип	Документы #674857

Титульный лист

Эконометрика

Рейтинговая работа

Вариант 12

Содержание

Задание 2

Выполнение Задания 3

1. Построение линейной модели парной регрессии 3

2. Расчет коэффициента корреляции 5

3. Расчет коэффициента эластичности 6

4. Прогноз на следующий шаг 6

Список использованной литературы 8

Задание

1. Построить модель парной линейной регрессии y = a + bx +e.

2. Изобразить на графике исходные и модельные значения.

3. Рассчитать коэффициенты корреляции и эластичности, коэффициенты эластичности сопоставить с коэффициентами регрессии.

4. Сделать прогноз на следующий шаг.

Таблица 1

Исходные данные

X	19,6	34,1	39,2	34,2	26,9	43,2	34,1	39,2	24,1	27,4	50,9
Y	43	76	91	66	53	87	76	91	49	54	102

Выполнение Задания

1. Построение линейной модели парной регрессии

Общий вид линейного уравнения парной регрессии:

, где

- расчетные теоретические значения результативного признака для i-го наблюдения;

a и b – параметры линейного уравнения парной регрессии;

b– коэффициент регрессии, который показывает на сколько в среднем изменяется значение результативного признака у при увеличении фактора х на единицу измерения;

x_i– значение факторного признака для i-го наблюдения.

Параметры линейного уравнения найдем с помощью метода наименьших квадратов (МНК). Для определения параметров необходимо решить систему линейных уравнений /(систему нормальных уравнений):

Вспомогательные расчеты приведены в таблице 2.

Таблица 2

Вспомогательная таблица для расчета коэффициента корреляции и

построения модели

№
1	19,6	43	384,16	842,8	1849	41,41
2	34,1	76	1162,81	2591,6	5776	72,06
3	39,2	91	1536,64	3567,2	8281	82,84
4	34,2	66	1169,64	2257,2	4356	72,27
5	26,9	53	723,61	1425,7	2809	56,84
6	43,2	87	1866,24	3758,4	7569	91,29
7	34,1	76	1162,81	2591,6	5776	72,06
8	39,2	91	1536,64	3567,2	8281	82,84
9	24,1	49	580,81	1180,9	2401	50,92
10	27,4	54	750,76	1479,6	2916	57,90
11	50,9	102	2590,81	5191,8	10404	107,57
Итого	372,9	788	13464,9	28454	60418	788
Среднее	33,900	71,636	1224,085	2586,727	5492,545

Для расчета параметров можно использовать готовые формулы, которые вытекают из данной системы:

= 71,636 – 2,114×33,9 = -0,015

Получили линейное уравнение парной регрессии:

-0,015 + 2,114

Вывод. Коэффициент регрессии b показывает, что при увеличении факторного признака х на 1 единицу значение результативного признака у в среднем возрастает на 2,114 единицы. Поскольку значение положительное, то связь между признаками прямая.

Свободный член а= -0,015 оценивает влияние прочих факторов, оказывающих воздействие на результативный признак. Т.е. воздействие прочих факторов уменьшает значение результативного признака.

Теоретические (расчетные) значения результативного признака

получаем путем последовательной подстановки значений факторного признака

в уравнение регрессии.

Расчет представлен в последнем столбце таблицы 2.

График фактических значений (поле корреляции) и линия регрессии приведены на рисунке 1.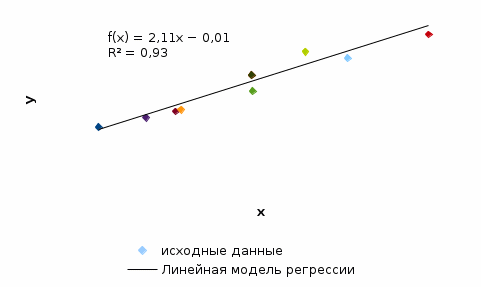

Рисунок 1 – Результаты моделирования

2. Расчет коэффициента корреляции

Коэффициент корреляции показывает тесноту и направление линейной связи между переменными. Чем ближе значение коэффициента к единице (по модулю), тем более тесная связь между признаками.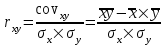

, где

- средние квадратические отклонения признаков.

Расчет средний квадратических отклонений:

Расчет коэффициента корреляции: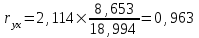

Вывод. Коэффициент корреляции показывает, что связь между признаками очень тесная и прямая.

Коэффициент детерминации характеризует долю вариации результативного признака под влиянием фактора, включенного в модель.

Вывод. 92,7% вариации результативного признака у происходит под влиянием факторного признака х. Остальные 7,3% вариации результативного признака у объясняется влиянием прочих случайных факторов, неучтенных в модели.

3. Расчет коэффициента эластичности

Коэффициент эластичности показывает, на сколько процентов в среднем изменяется значение результативного признака у при увеличении факторного признака х на 1%.

Расчет коэффициента эластичности: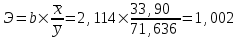

Вывод. Коэффициент эластичности показывает, что при увеличении факторного признака х на 1 % значение результативного признака у в среднем возрастает на 1,002%.

4. Прогноз на следующий шаг

Рассчитаем средний абсолютный прирост факторного признака:

Прогнозное значение фактора: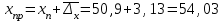

Прогнозное значение результативного признака (точечный прогноз):

Вывод. По построенной линейной модели регрессии можно ожидать, что в следующем периоде значение результативного признака составит 114,183 единицы.

Список использованной литературы

Басовский, Л.Е. Эконометрика [Электронный ресурс] : учеб. пособие / Л.Е. Басовский. — М.: РИОР: ИНФРА-М, 2017. — 48 с. – Режим доступа: http://znanium.com/bookread2.php?book=559446
Елисеева: учебник для магистров / И.И. Елисеева [и др]; под ред. И.И. Елисеевой. – М.: Издательство Юрайт, 2014. – 453 с.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред.проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный уцрс: Учеб. – 6-е изд., перераб. и доп. – М.: дело, 2004. – 576 с.
Новиков А.И. Эконометрика: Учебное пособие. – М.: Российский университет кооперации, 2008. – 137 с.