Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb.
|
|
Тема 2. Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии Термином регрессия (лат. regressio – обратное движение, отход) обозначают зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Этот термин впервые был использован Френсисом Гальтоном при исследовании вопросов наследования физических характеристик человека. В качестве одной из характеристик был взят рост человека; при этом было обнаружено, что в целом сыновья высоких отцов оказались более высокими, чем сыновья отцов с низким ростом, притом, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения роста сыновей к среднему (regression to mediocrity), то есть «регресс». Функцией регрессии y по X=(x1,…,xn) называют функцию, которая описывает изменение условного математического ожидания (среднего значения) зависимой переменной yв зависимости от изменения независимых переменныхX, принимающих фиксированные значения Х*:  Функцию регрессии также называют уравнением регрессии, моделью регрессии или просто регрессией. Ее математическую запись также часто приводят в упрощенном виде:  Учитывая, что зависимость между переменными y и X мы рассматриваем как стохастическую, модель регрессии можно записать в следующем виде:  где ε – случайная ошибка модели. В регрессионных моделях эту величину отождествляют с влиянием факторов, не включенных в модель. Случайная ошибка определяется как разность между фактическим значением зависимой переменной yи значением ее математического ожидания  , которое в моделях регрессии обычно обозначают  : Таким образом, построение модели регрессии включает в себя с одной стороны спецификацию и идентификацию функции , а с другой – оценку свойств значений случайной ошибки ε, соответствующих этой функции.Рассмотрим проблему спецификации модели регрессии, включающей одну зависимую переменную (результат) y и одну независимую переменную (фактор) x. С учетом того, что X=(x), модель регрессии y по X примет вид:  В этом случае задача спецификации сводиться к определению вида математической функции  , что может быть осуществлено тремя методами:графическим; аналитическим (теоретическим); экспериментальным (эмпирическим). Неверный выбор вида математической функции используемой при построении модели регрессии является одной из причин возникновения ошибок спецификации. Другой причиной выступает недоучет влияния факторов, оказывающих существенное воздействие на результативную переменную, но не включенных в модель. Следствием наличия ошибок спецификации является искажение величины регрессионных остатков, особенности анализа которых, а также методы определения целесообразности включения дополнительных факторов в модель будут рассмотрены нами позже. Графический метод определения вида математической функции заключается в построении и анализе поля корреляции (диаграммы рассеяния). Поле корреляции представляет собой графическое изображение совместного распределения двух переменных в ортогональной системе координат. При этом каждая пара наблюдений, характеризующая отдельные значения переменных x и y изображается на графике в виде точки (или аналогичного символа). Пример 2.1. В качестве примера построения поля корреляции используем данные о среднедушевых денежных доходах населения и среднемесячном обороте розничной торговли на душу населения регионов центрального федерального округа Российской Федерации за 2010 г. (таблица 2.1.1). Таблица 2.1.1 Среднедушевые денежные доходы оборот розничной торговли на душу населения регионов центрального федерального округа Российской Федерации за 2010 г.
Учитывая, что доходы населения выступают фактором, определяющим величину оборота розничной торговли, отложим значения доходов по оси абсцисс (x), а значения оборота – по оси ординат (y) (рисунок 2.1.1).  Рис. 2.1.1. Поле корреляции (диаграмма рассеяния) оборота розничной торговли на душу населения и величины среднедушевых денежных доходов населения На представленном графике каждая точка соответствует определенному региону. Общее количество точек равно 18, то есть совпадает с числом наблюдений, в нашем конкретном случае – с числом регионов в центральном федеральном округе. Рассмотрим построение поля корреляции в программе для работы с электронными таблицами Microsoft Office Excel: Шаг 1. На вкладке «Вставка» выбираем блок «Диаграммы», тип диаграммы «Точечная», вид диаграммы «Точечная с маркерами»:  Альтернативным вариантом может быть выбор кнопки «Создание диаграммы»:  Выбор в появившемся диалоговом окне вида диаграммы «Точечная с маркерами»:  Шаг 2. Для добавления данных на график можно воспользоваться кнопкой «Выбрать данные»:  Или вызвать контекстное меню, щелкнув правой кнопкой мыши на поле диаграммы:  В появившемся диалоговом окне «Выбор источника данных» следует нажать на кнопку «Добавить»:  В диалоговом окне «Изменение ряда» в поле «Значения Х» следует указать ссылку на столбец содержащий значения независимой переменной, откладываемые на оси абсцисс, а в поле «Значения Y» - на столбец содержащий значения зависимой переменной, откладываемые по оси ординат:  Построенное поле корреляции подвергают визуальному анализу. Если точки на нем расположены вдоль воображаемой кривой (заметим, что и прямая линия – это математическая кривая) то это означает, что между исследуемыми переменными существует зависимость. Вид полученной кривой характеризует форму зависимости (линейную или нелинейную) и чаще всего способен подсказать какая именно математическая функция будет использована для построения модели регрессии. При визуальном анализе наиболее часто определяются зависимости между экономическими переменными, которые описываются следующими функциями:  Рис. 2.1.2. Линейная функция 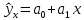 . Рис. 2.1.2. Функция  (гипербола). Рис. 2.1.2. Квадратичная функция (парабола)  . Рис. 2.1.2. Степенная функция  .По виду поля корреляции можно судить о тесноте зависимости между исследуемыми переменными – чем ближе точки расположены к воображаемой кривой, тем теснее связь между переменными. Если на основе визуального анализа установлено, что зависимость между исследуемыми переменными линейна, то есть воображаемая кривая является прямой линией, то количественно тесноту такой зависимости можно охарактеризовать при помощи ковариации и линейного коэффициента корреляции. Ковариация или корреляционный момент определяется по формуле:  .Ковариация имеет размерность, равную произведению размерности исследуемых переменных, то есть величина ковариации зависит от их единиц измерения. Это существенно затрудняет использование ковариации при исследовании зависимости между экономическими величинами. Этого недостатка лишен линейный коэффициент корреляции (коэффициент Пирсона), рассчитываемый по формуле:  где  – стандартное (среднее квадратическое) отклонение переменной x; – стандартное (среднее квадратическое) отклонение переменной y.Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Знак коэффициента характеризует направление связи: «+» означает, что связь прямая, «-» – что связь обратная. Прямая или положительная корреляционная связь означает, что при увеличении или уменьшении одной переменной среднее значение другой переменной изменяется с тем же знаком. Если при изменении одной переменной среднее значение другой переменной изменяется с противоположным знаком – то такая связь называется обратной или отрицательной. Направление связи можно оценить при визуальном анализе поля корреляции: если точки на нем расположены «слево-направо» и «снизу-вверх», то можно предположить наличие прямой зависимости, а если «слево-направо» и «сверху-вниз», то – обратной. Примеры проявления прямой и обратной связи на корреляционном поле представлены на рисунке:  Рис. 2.1.4. Прямая (левый график) и обратная (правый график) зависимость между переменными Абсолютное значение коэффициента корреляции характеризует тесноту связи. Чем ближе оно к 1, тем теснее зависимость между переменными. Для качественной интерпретации значений коэффициента корреляции часто используют шкалу Чеддока:
|