Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Аналитический метод выбора вида математической функции при спецификации модели регрессии основан на изучении теоретических основ возникновения взаимосвязи между исследуемыми переменными. Как правило, в эконометрике эти теоретические основы являются предметом изучения экономической теории. Например, нам известно, что зависимость спроса от цены, изображенная графически, имеет вид гиперболы, зависимость потребления от дохода имеет предел насыщения и поэтому ее можно представить в виде логистической кривой. Величина налоговых поступлений в бюджет зависит от ставки налогов, что описывается кривой Лаффера, имеющей форму параболы. Мы привели лишь малую часть зависимостей между экономическими переменными, зная качественное содержание которых можно априорно выбрать вид математической функции для модели регрессии. Однако не будем забывать, что одной из целей эконометрики как раз и является эмпирическая проверка положений экономической теории на реальных статистических данных. Поэтому даже если вид функции был выбран при помощи аналитического метода, абсолютно не лишним будет визуальный анализ исходных данных и проверка спецификации экспериментальным методом. Экспериментальный метод выбора математической функции, используемой при построении модели регрессии заключается в сравнении сумм квадратов регрессионных остатков рассчитанных для различных видов функций. Пример таких расчетов мы рассмотрим позднее, когда будем уметь рассчитывать оценки параметров линейных и нелинейных моделей. Применение экспериментального метода не требует высокой квалификации исследователя, и в этой связи пользуется значительной популярностью. Однако следует заметить, что вид математической функции выбранный при помощи экспериментального метода, должен находиться во множестве видов функций допустимых и объясняемых в рамках аналитического метода. Другими словами – если вид функции выбранный на основе минимизации суммы квадратов регрессионных остатков не может быть содержательно интерпретирован в границах теоретической базы исследования, то от этой функции следует отказаться. В общем случае можно говорить, что если отсутствуют теоретические предпосылки к использованию нелинейных функций, то целесообразно использовать линейные модели, даже если они обладают несколько худшими характеристиками регрессионных остатков. Если форма распределения исследуемых переменных делает невозможным использование линейной модели, то построение нелинейной модели должно сопровождаться формированием нового теоретического обоснования взаимосвязи между экономическими величинами. 2. Оценка параметров модели парной линейной регрессии Моделью парной линейной регрессии называют уравнение вида: 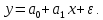 Название парной данная модель получила в силу того, что в ней содержатся лишь две переменные: зависимая или результатирующая переменная yи независимая или факторная переменнаяx. Модель называется линейной, поскольку при ее спецификации используется линейная функция (уравнение прямой). Величины 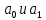 являются параметрами модели. являются параметрами модели. Параметр 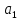 называют коэффициентом регрессии. Он характеризует среднее изменение результата yпри изменении фактораxна единицу. называют коэффициентом регрессии. Он характеризует среднее изменение результата yпри изменении фактораxна единицу.Параметр 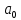 называют свободным членом. Он характеризует значение результата yпри нулевом значении фактораx. Следует отметить, что не всегда эта величина имеет экономический смысл, в частности невозможно интерпретировать значение называют свободным членом. Он характеризует значение результата yпри нулевом значении фактораx. Следует отметить, что не всегда эта величина имеет экономический смысл, в частности невозможно интерпретировать значение 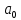 если фактор xв принципе не может обращаться в ноль. Содержательной интерпретации поддается знак параметра если фактор xв принципе не может обращаться в ноль. Содержательной интерпретации поддается знак параметра 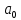 , так если он положительный, то относительное изменение результата происходит медленнее, чем изменение фактора, при этом справедливо и обратное утверждение. , так если он положительный, то относительное изменение результата происходит медленнее, чем изменение фактора, при этом справедливо и обратное утверждение. Графически параметры модели парной линейной регрессии можно представить следующим образом: 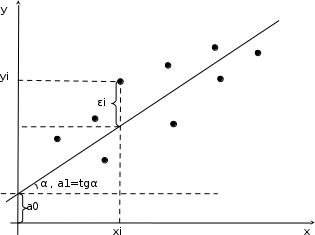 Рис. 2.2.1. Графическое представление модели парной линейной регрессии Мы видим, что параметр 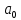 определяет смещение по вертикали линии регрессии, задаваемой уравнением определяет смещение по вертикали линии регрессии, задаваемой уравнением 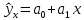 . В свою очередь, параметр . В свою очередь, параметр 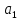 равен тангенсу угла α между линией регрессии и осью абсцисс. Параметр равен тангенсу угла α между линией регрессии и осью абсцисс. Параметр 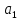 часто называют угловым коэффициентом. часто называют угловым коэффициентом. Ошибки регрессии ε представляют собой разницу ординат точек соответствующих фактическим значением переменной yи лежащих на линии регрессии при одних и тех же значениях фактора x. Значение ошибки для конкретного наблюдения можно определить по формуле: 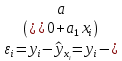 . .Для нахождения оценок (приближенных значений) параметров модели регрессии необходимо выбрать критерий, по которому мы будем определять их оптимальность. Наиболее распространенными являются следующие критерии: Критерий суммы квадратов отклонений фактических значений зависимой переменной (y) от ее теоретических или расчетных значений ( 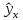 ): ):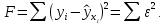 Достоинствами данного критерия выступают простота вычислительных процедур и доступность математических выводов, в то время как основным недостатком – излишняя чувствительность оценок параметров к выбросам в исходных данных. Критерий суммы модулей отклонений фактических значений зависимой переменной (y) от ее теоретических или расчетных значений ( 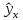 ): ):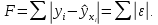 Преимуществом данного критерия является устойчивость к резким выбросам в исходных данных, а недостатком – сложности в процессе вычислений. Критерий суммы отклонений фактических значений зависимой переменной (y) от ее теоретических или расчетных значений ( 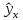 ) с учетом заданных весов g: ) с учетом заданных весов g: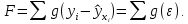 Для задания весов gможет использоваться функция Хубера:  где с – ограничение функции. Данная функция при небольших значениях регрессионных остатков является квадратичной, а при больших – линейной. Наиболее распространенным критерием, используемым при оценке параметров модели регрессии является критерий суммы квадратов отклонений, а метод оценки параметров основанный на его использовании называется методом наименьших квадратов (МНК). Содержание МНК состоит в нахождении оценок неизвестных параметров ( 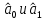 ) минимизирующих функцию: ) минимизирующих функцию: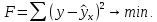 Учитывая, что 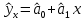 получим следующее выражение: получим следующее выражение: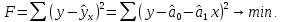 Для нахождения минимума функции F необходимо определить и прировнять к нулю частные производные функции по 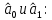 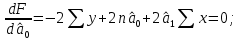 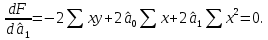 Приведенное выражение сводится к системе нормальных уравнений, имеющей следующий вид: 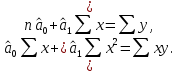 Решением системы нормальных уравнений являются оценки параметров модели регрессии, рассчитываемые по следующим формулам: 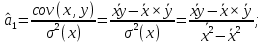 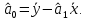 Таким образом, при заданной спецификации модели значения оценок ее параметров зависят, во-первых, от выбранного критерия оптимизации, а, во-вторых, от числовых характеристик выборки из генеральной совокупности ( 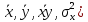 используемых при расчетах. используемых при расчетах. Эконометрика имеет дело с выборочными данными. Даже если используемые данные охватывают всю совокупность наблюдений, доступных для анализа, то реализация эконометрических задач, а именно имитации и прогноза, неизбежно предполагает выход за границы имеющихся наблюдений. Поэтому при заданном критерии оптимизации (в качестве которого мы будем использовать МНК) число оценок параметров равно числу возможных выборок из генеральной совокупности. Пример 2.4. Рассмотрим расчет оценок параметров модели парной линейной регрессии на примере данных о среднедушевых денежных доходах населения и среднемесячном обороте розничной торговли на душу населения регионов центрального федерального округа Российской Федерации за 2010 г. с учетом устранения выбросов. Для удобства вычислений составим рабочую таблицу (таблица 2.2.1). 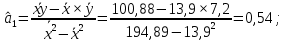  Таким образом, модель регрессии примет вид: 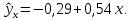 Таблица 2.2.1 Данные для расчета оценок параметров модели парной линейной регрессии оборота розничной торговли по величине денежных доходов населения
Графическое изображение линии регрессии представлено на рисунке 2.2.1. 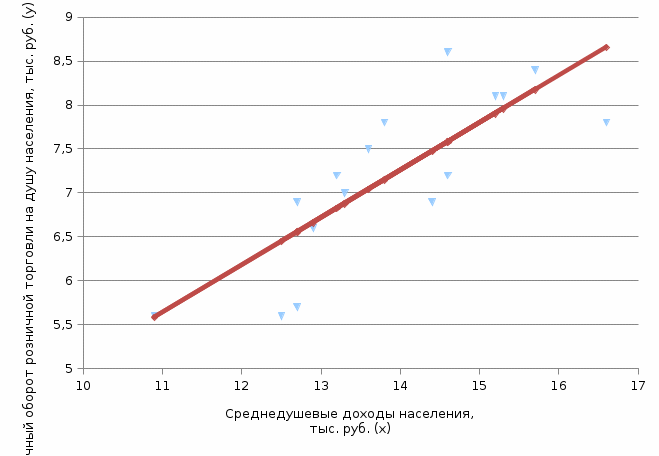 Рис. 2.2.1. Линия регрессии оборота розничной торговли на душу населения по величине среднедушевых денежных доходов населения Параметр 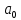 , оценка которого составила -0,29, в нашем примере не будет иметь экономического смысла, поскольку фактор x (доходы населения региона) не может принимать нулевое значение. В то же время отрицательный знак параметра показывает, что изменение результата (оборота розничной торговли) происходит быстрее, чем изменение названного фактора. , оценка которого составила -0,29, в нашем примере не будет иметь экономического смысла, поскольку фактор x (доходы населения региона) не может принимать нулевое значение. В то же время отрицательный знак параметра показывает, что изменение результата (оборота розничной торговли) происходит быстрее, чем изменение названного фактора.Параметр 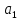 , оценка которого составила 0,54, свидетельствует о том, что при изменении доходов населения на 1 руб. (тыс. руб.), среднее изменение оборота розничной торговли составит 0,54 руб. (тыс. руб.). , оценка которого составила 0,54, свидетельствует о том, что при изменении доходов населения на 1 руб. (тыс. руб.), среднее изменение оборота розничной торговли составит 0,54 руб. (тыс. руб.).Расчет оценки коэффициента регрессии возможен также на основе значения выборочного коэффициента корреляции: 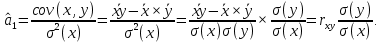 Относительное изменение результативной переменной при изменении факторной переменной на 1% характеризует коэффициент эластичности:  где 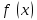 - первая производная функции - первая производная функции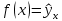 . .Учитывая, что для линейной функции 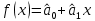 равен равен 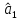 , коэффициент эластичности для модели парной линейной регрессии можно рассчитать по формуле: , коэффициент эластичности для модели парной линейной регрессии можно рассчитать по формуле: Поскольку коэффициент эластичности линейной функции не является постоянной величиной, так как зависит от значений переменной x, на практике обычно рассчитывают средний коэффициент эластичности который показывает на сколько процентов в среднем изменится значение результативной переменной y при изменении факторной переменной x на 1%: 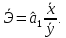 Расчет коэффициента эластичности не имеет экономического смысла в том случае когда нецелесообразно измерять изменение исследуемых переменных при помощи темпов прироста (например возраст человека, число членов семьи, стаж работы и т.п.). Пример 2.5. В нашем примере средний коэффициент эластичности равен: 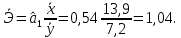 Таким образом при изменении среднедушевых денежных доходов населения на 1%, оборот розничной торговли на душу населения в среднем изменяется на 1,04%. 3. Свойства оценок параметров модели регрессии полученных по МНК Оценки параметров модели регрессии полученные при использовании МНК (МНК-оценки) являются BLUE, что расшифровывается как наилучшая (Best) линейная (Linear) несмещенная (Unbiased) оценка (Estimator). Альтернативной формулировкой требований к оценкам параметров являются свойства состоятельности, эффективности и несмещенности оценок. Рассмотрим формулировку этих свойств. |
