Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Проверка статистической значимости параметра модели регрессии 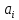 заключается в проверке нулевой гипотезы о равенстве нулю его значения в генеральной совокупности: заключается в проверке нулевой гипотезы о равенстве нулю его значения в генеральной совокупности: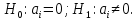 Для проверки выдвинутой гипотезы используется t-критерий, подчиняющийся распределению Стьюдента: 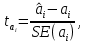 где 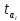 – t-критерий для параметра – t-критерий для параметра 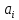 ; ;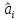 – оценка параметра – оценка параметра 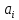 в выборочной совокупности; в выборочной совокупности;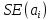 – стандартная ошибка параметра – стандартная ошибка параметра 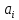 . .t-критерий показывает во сколько раз разность между оценкой параметра и его истинным значением больше стандартной ошибки параметра. Учитывая, что согласно выдвинутой гипотезе 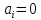 , а стандартная ошибка параметра представляет собой стандартное отклонение его выборочной оценки , а стандартная ошибка параметра представляет собой стандартное отклонение его выборочной оценки 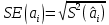 , формулу для расчета t-критерия можно представить в следующем виде: , формулу для расчета t-критерия можно представить в следующем виде: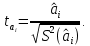 Критическое значение t-критерия ( 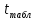 ) определяется по таблицам распределения Стьюдента для проверки двусторонних (two tailed) гипотез при заданном уровне значимости ) определяется по таблицам распределения Стьюдента для проверки двусторонних (two tailed) гипотез при заданном уровне значимости 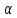 и числе степеней свободы и числе степеней свободы 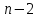 . Если используются таблицы распределения Стьюдента для проверки односторонних (one tailed) гипотез, следует указывать уровень значимости . Если используются таблицы распределения Стьюдента для проверки односторонних (one tailed) гипотез, следует указывать уровень значимости 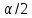 . .Область допустимых значений задается условием 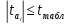 , а критическая область – условием , а критическая область – условием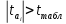 . . Таким образом, если рассчитанное по выборочным данным значение t-критерия больше критического значения ( 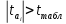 ), то нулевая гипотеза о равенстве нулю параметра регрессии отвергается с вероятностью ошибки ), то нулевая гипотеза о равенстве нулю параметра регрессии отвергается с вероятностью ошибки 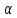 и параметр считается статистически значимым. и параметр считается статистически значимым.Если рассчитанное по выборочным данным значение t-критерия меньше или равно критическому значению ( 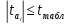 ), то нулевая гипотеза о равенстве нулю параметра регрессии принимается и параметр регрессии считается статистически незначимым. ), то нулевая гипотеза о равенстве нулю параметра регрессии принимается и параметр регрессии считается статистически незначимым.С учетом рассмотренных выше формул оценки дисперсии МНК-оценок параметров парной линейной регрессии, формулы для расчета t-критерия будут иметь следующий вид: 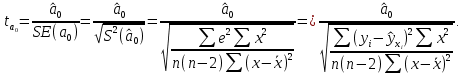 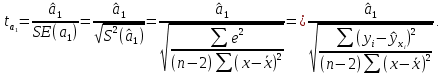 Пример 2.8. Рассмотрим оценку статистической значимости параметров модели парной линейной регрессии на примере зависимости между оборотом розничной торговли и доходами населения регионов Центрального федерального округа. Исходные данные для анализа представлены в таблице 2.6.3. Таблица 2.6.3 Исходные данные для анализа статистической значимости параметров регрессии
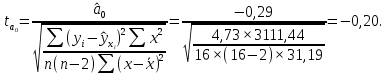 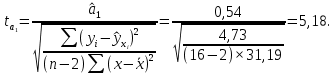 Определим критическое значение t-критерия по таблице распределения Стьюдента для проверки двусторонних гипотез: 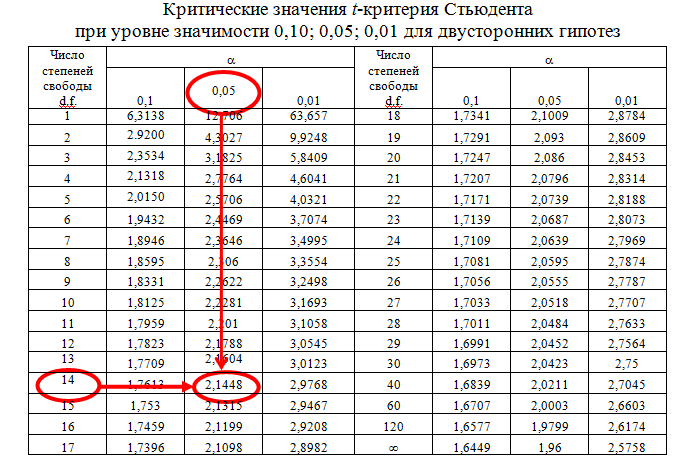 Расчетное значение t-критерия для параметра 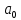 попадает в область принятия гипотезы попадает в область принятия гипотезы 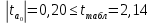 , следовательно мы не можем отклонить нулевую гипотезу о его равенстве нулю с приемлемой вероятностью ошибки. Однако ранее мы отмечали, что в построенной нами модели параметр , следовательно мы не можем отклонить нулевую гипотезу о его равенстве нулю с приемлемой вероятностью ошибки. Однако ранее мы отмечали, что в построенной нами модели параметр 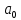 не имеет экономического смысла и, соответственно, мы можем не делать никаких предположений относительно его значения. не имеет экономического смысла и, соответственно, мы можем не делать никаких предположений относительно его значения.Расчетное значение t-критерия для параметра 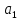 попадает в критическую область попадает в критическую область 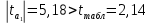 , следовательно с вероятностью 95% мы отвергаем нулевую гипотезу о равенстве нулю коэффициента регрессии и считаем его статистически значимым. , следовательно с вероятностью 95% мы отвергаем нулевую гипотезу о равенстве нулю коэффициента регрессии и считаем его статистически значимым.Табличное значение t-критерия можно получить используя функцию СТЬЮДРАСПОБР из категории «Статистические» в Microsoft Office Excel: 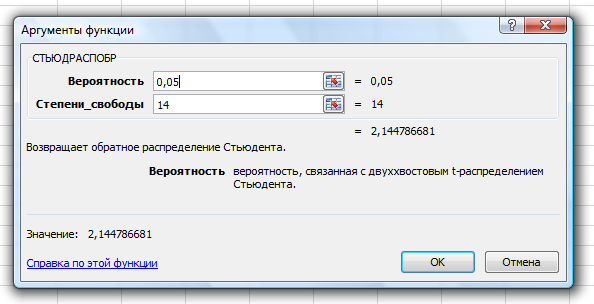 В диалоговом окне функции необходимо: в поле «Вероятность» - ввести уровень значимости (обычно 0,05 или 5%); в поле «Степени_свободы» ввести число степеней свободы для объясненной суммы квадратов отклонений (в модели парной линейной регрессии – 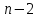 , в нашем примере 16-2=14). , в нашем примере 16-2=14).Полученное значение t-критерия равное 2,14 совпадает с тем значением, которое мы определили по таблице t-распределения. С помощью функции СТЬЮДРАСПР входящей в категорию «Статистические» Microsoft Office Excel возможно по рассчитанному значению t-критерия определить соответствующую ему р-величину: 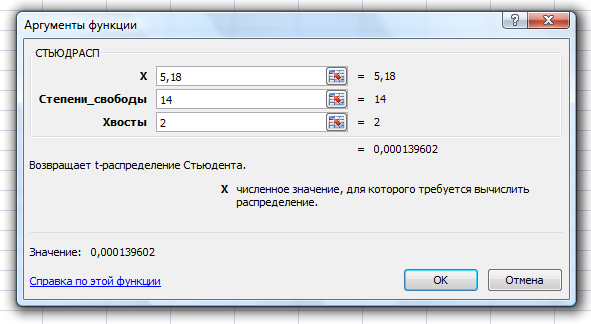 В диалоговом окне функции необходимо: в поле «Х» - ввести рассчитанное по выборочным данным значение t-критерия (в нашем примере 5,18); в поле «Степени_свободы» ввести число степеней свободы для объясненной суммы квадратов отклонений (в модели парной линейной регрессии – 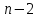 , в нашем примере 16-2=14); , в нашем примере 16-2=14);в поле «Хвосты» ввести число 2, поскольку t-критерий используется для проверки двухсторонней гипотезы. р-значение  говорит нам о том, что вероятность ошибки при отклонении нулевой гипотезы составляет говорит нам о том, что вероятность ошибки при отклонении нулевой гипотезы составляет 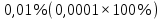 . Таким образом, вероятность того, что коэффициент регрессии принимает значение, отличное от нуля, составляет 99,99%. . Таким образом, вероятность того, что коэффициент регрессии принимает значение, отличное от нуля, составляет 99,99%.Проверка статистической значимости линейного коэффициента корреляции 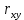 заключается в проверке нулевой гипотезы о равенстве нулю его значения в генеральной совокупности: заключается в проверке нулевой гипотезы о равенстве нулю его значения в генеральной совокупности: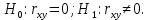 Учитывая, что стандартная ошибка коэффициента корреляции определяется по формуле: 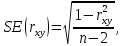 расчетное значение t-критерия составит: 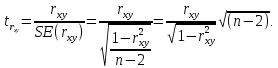 Порядок проверки нулевой гипотезы относительно значения коэффициента корреляции с использованием t-критерия аналогичен проверке гипотезы о значении параметров модели регрессии. Применение t-критерия для проверки гипотезы о равенстве нулю коэффициента корреляции целесообразно при выполнении следующих условий: значительное число наблюдений (объем выборки 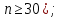 абсолютное значение коэффициента корреляции значительно меньше 1 ( 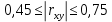 ). ).Если указанные условия не выполняются, то распределение оценок коэффициента корреляции не подчиняется нормальному распределению, в силу того, что их значения ограничены интервалом 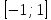 . .Для решения данной проблемы Р. Фишером было предложено использовать вспомогательную нормально распределенную величину 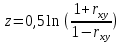 , имеющую стандартную ошибку , имеющую стандартную ошибку 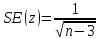 . .Рассчитанное значение критерия: 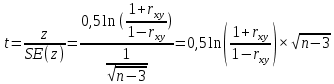 сопоставляют с табличным значением, определенным по таблице нормального распределения с заданным уровнем значимости 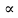 . . Пример 2.9. Рассмотрим пример оценки статистической значимости коэффициента корреляции между оборотом розничной торговли и величиной доходов населения, рассчитанным по данным 16 регионов Центрального федерального округа: 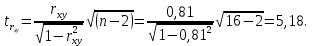 Рассчитанное значение 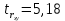 превышает табличное значение превышает табличное значение 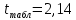 при при 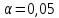 , и следовательно коэффициент корреляции между оборотом розничной торговли и величиной доходов населения является статистически значимым. , и следовательно коэффициент корреляции между оборотом розничной торговли и величиной доходов населения является статистически значимым.Однако исходные данные не удовлетворяют условиям использования t-критерия. Поэтому проведем оценку статистической значимости коэффициента корреляции с использованием преобразования Фишера: 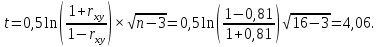 Табличное значение критерия определим, используя функцию НОРМСТОБР входящую в категорию «Статистические» Microsoft Office Excel: 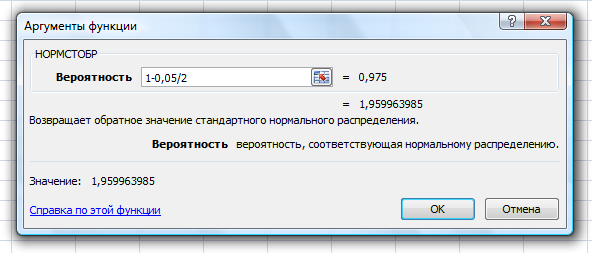 Поскольку проверяемая гипотеза является двухсторонней, а нормальное распределение – симметричным, в поле «Вероятность» необходимо указать величину 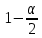 . .Поскольку рассчитанное значение критерия (4,06) превышает табличное (1,96), нулевая гипотеза о равенстве нулю коэффициента корреляции отвергается с вероятностью ошибки 5%, и коэффициент корреляции между оборотом розничной торговли и доходами населения является статистически значимым. Учитывая, что 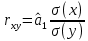 , а , а 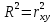 мы можем признать равносильными гипотезы мы можем признать равносильными гипотезы 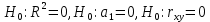 . Таким образом, если уравнение парной регрессии в целом статистически значимо, то статистически значимыми являются коэффициент регрессии и коэффициент корреляции. Поскольку квадрат случайной величины имеющей распределение Стьюдента имеет распределение Фишера можно записать следующее соотношение: . Таким образом, если уравнение парной регрессии в целом статистически значимо, то статистически значимыми являются коэффициент регрессии и коэффициент корреляции. Поскольку квадрат случайной величины имеющей распределение Стьюдента имеет распределение Фишера можно записать следующее соотношение: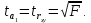 Действительно: 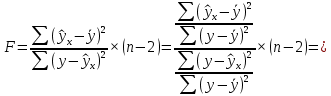 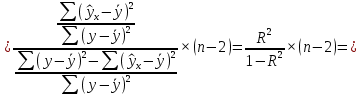 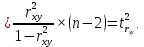 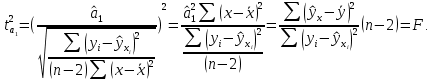 |