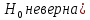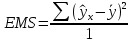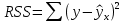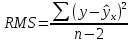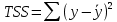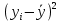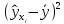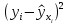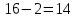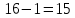Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
6. Оценка статистической значимости модели регрессии Оценка статистической значимости модели регрессии заключается в проверке статистических гипотез об истинных значениях параметров модели и показателей тесноты связи между исследуемыми переменными. Параметрической статистической гипотезой (далее статистической гипотезой) называют предположение о величине параметров известного распределения (генеральной совокупности). Проверка статистической гипотезы заключается в проверке соответствия выборочных данных выдвинутой гипотезе. Параллельно с выдвигаемой гипотезой рассматривают и противоречащую ей гипотезу, которая считается справедливой, если выдвинутая гипотеза отвергается. Выдвигаемую гипотезу называют нулевой, основной или проверяемой гипотезой и обозначают 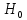 . .Гипотезу, противоречащую первоначальной, называют конкурирующей или альтернативной гипотезой и обозначают 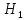 . .При проверке статистических гипотез можно допустить ошибки первого и второго рода. Ошибка первого рода возникает при опровержении верной гипотезы. Ошибка второго рода заключается в принятии ложной гипотезы:
Уровнем статистической значимости (или просто уровнем значимости) называют вероятность совершения ошибки первого рода. Уровень значимости обозначают буквой 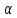 . Величину уровня значимости обычно принимают близкой к нулю, поскольку, чем меньше его значение, тем меньше вероятность совершения ошибки первого рода, состоящей в опровержении верной нулевой гипотезы. В экономических исследованиях уровень значимости обычно принимают равным 0,05 или 5%. . Величину уровня значимости обычно принимают близкой к нулю, поскольку, чем меньше его значение, тем меньше вероятность совершения ошибки первого рода, состоящей в опровержении верной нулевой гипотезы. В экономических исследованиях уровень значимости обычно принимают равным 0,05 или 5%. Проверка статистических гипотез осуществляется с использованием статистических критериев. Статистическим критерием называют случайную величину, подчиняющуюся определенному закону распределения. Названия статистических критериев соответствуют законам распределения: F-критерий соответствует распределению Фишера-Снедекора, 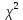 -критерий – -критерий – 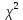 -распределению, t-критерий – распределению Стьюдента, U-критерий – нормальному распределению. -распределению, t-критерий – распределению Стьюдента, U-критерий – нормальному распределению.Множество всех возможных значений статистического критерия можно разделить на два непересекающихся подмножества. Первое подмножество (область допустимых значений или область принятия гипотезы) включает в себя те значения критерия, при которых нулевая гипотеза принимается, а второе подмножество (критическая область) охватывает те значения критерия, при которых нулевая гипотеза отвергается. Значения статистического критерия, разграничивающие критическую область и область принятия гипотезы, называют критическими точками (значениями) или квантилями. Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности. Если наблюдаемое значение статистического критерия принадлежит критической области, то нулевая гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то нулевая гипотеза принимается. Проверка статистической значимости модели регрессии в целом осуществляется путем проверки нулевой гипотезы о равенстве нулю коэффициента детерминации в генеральной совокупности: 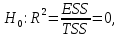 при конкурирующей гипотезе: 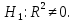 Содержание нулевой гипотезы означает, что объясненная сумма квадратов отклонений ESS равна нулю, то есть в генеральной совокупности 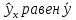 и не зависит от х. Очевидно, что в этой ситуации моделирование зависимости между выбранными переменными не имеет никакого смысла. и не зависит от х. Очевидно, что в этой ситуации моделирование зависимости между выбранными переменными не имеет никакого смысла.Сумма квадратов отклонений зависимой переменной TSS(а, следовательно, и ESS и RSS) является абсолютной величиной, которая среди прочего зависит от числа наблюдений. Для устранения влияния этого фактора при проверке нулевой гипотезы рассчитывают среднюю сумму квадратов отклонений (MiddleSumofSquare, MSS) которая получила название дисперсии на одну степень свободы. Степень свободы (degreeoffreedom, df) это количество значений в итоговом вычислении выборочного показателя, способных варьироваться. Применительно к регрессионному анализу, число степеней свободы показывает сколько независимых отклонений из n возможных необходимо для образования их суммы квадратов. Число степеней свободы различно для каждой из сумм квадратов отклонений. Так число степеней свободы для TSSсоставляет n-1. Действительно, в силу 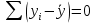 необходимо знать только n-1 значение отклонений, чтобы рассчитать сумму их квадратов. Например, пусть необходимо знать только n-1 значение отклонений, чтобы рассчитать сумму их квадратов. Например, пусть 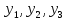 значения переменной y, тогда сумму значения переменной y, тогда сумму 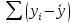 можно определить как можно определить как 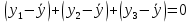 , откуда , откуда 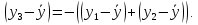 Число степеней свободы для ESSв модели парной линейной регрессии равно 1. Для доказательства этого утверждения запишем уравнение регрессии в следующем виде: 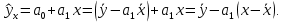 Таким образом, в модели парной регрессии величина 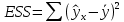 определяется значением определяется значением 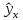 , которое при заданном наборе значений переменных xи yявляется функцией только одного параметра , которое при заданном наборе значений переменных xи yявляется функцией только одного параметра 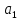 . .Следует отметить, что в общем случае, число степеней свободы для факторной суммы квадратов отклонений равно числу факторов, включенных в модель. Число степеней свободы для RSSв модели парной линейной регрессии равно n-2. Эта величина определяется как разность между числом наблюдений и числом оцениваемых параметров, которое в модели парной линейной регрессии равно 2 ( 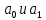 ). ).Число степеней свободы, как и суммы квадратов отклонений, можно складывать между собой: 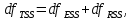 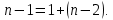 Расчет дисперсии на одну степень свободы приводит суммы квадратов отклонений к сопоставимому виду: - общая дисперсия на одну степень свободы (TotalMiddleSumofSquare, TMS): 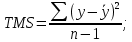 факторная дисперсия на одну степень свободы (ExplainedMiddleSumofSquare, EMS): 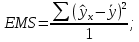 остаточная дисперсия на одну степень свободы (ResidualMiddleSumofSquare, RMS): 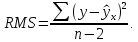 Разложение общей дисперсии признака на составляющее получило название дисперсионного анализа или ANOVA(ANalysisOfVAariance). Результаты дисперсионного анализа обычно оформляют в виде таблицы:
Однако, величина дисперсии на одну степень свободы, даже после устранения влияния числа наблюдений, зависит от размерности результативной переменной. Поэтому для оценки значимости модели регрессии используют отношение факторной и остаточной дисперсии на одну степень свободы. Эта величина, подчиняющаяся распределению Фишера-Снедекора, в эконометрике называется F-критерием или F-критерием Фишера: 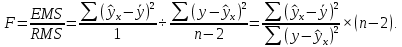 Критическое (табличное) значение F-критерия ( 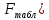 определяется по таблице распределения Фишера-Снедекора с учетом заданного уровня значимости определяется по таблице распределения Фишера-Снедекора с учетом заданного уровня значимости 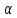 и числа степеней свободы и числа степеней свободы 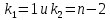 . .Область допустимых значений задается условием 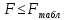 , а критическая область – условием , а критическая область – условием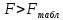 . . Таким образом, если рассчитанное по выборочным данным значение F-критерия больше критического значения ( 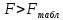 ), то нулевая гипотеза о равенстве нулю коэффициента детерминации, а, следовательно, случайном характере связи между переменными отвергается с вероятностью ошибки ), то нулевая гипотеза о равенстве нулю коэффициента детерминации, а, следовательно, случайном характере связи между переменными отвергается с вероятностью ошибки 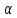 и модель регрессии в целом считается статистически значимой. и модель регрессии в целом считается статистически значимой.Если рассчитанное по выборочным данным значение F-критерия меньше или равно критическому значению ( 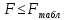 ), то нулевая гипотеза о равенстве нулю коэффициента детерминации, а, следовательно, случайном характере связи между переменными принимается и модель регрессии в целом считается статистически незначимой. ), то нулевая гипотеза о равенстве нулю коэффициента детерминации, а, следовательно, случайном характере связи между переменными принимается и модель регрессии в целом считается статистически незначимой.Проверка статистических гипотез о значимости модели регрессии осуществляется при помощи параметрических критериев основанных на нормальном распределении. Следовательно, к предпосылкам применения МНК для оценки параметров регрессии добавляется еще одно допущение – о нормальном распределении ошибок регрессии. Статистические критерии, используемые для проверки нормальности распределения, будут рассмотрены нами далее. Сейчас же мы предполагаем, что рассматриваемая предпосылка выполняется. Пример 2.7. Рассмотрим оценку статистической значимости модели парной линейной регрессии на примере зависимости между оборотом розничной торговли и доходами населения регионов Центрального федерального округа. Исходные данные для дисперсионного анализа результатов регрессии представлены в таблице 2.6.1. Таблица 2.6.1 Исходные данные для дисперсионного анализа результатов регрессии
Составим таблицу показателей дисперсионного анализа результатов регрессии (табл. 2.6.2). Таблица 2.6.2 Дисперсионный анализ результатов регрессии
Рассчитаем значение F-критерия по данным дисперсионного анализа: 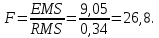 Тот же результат получим, используя значения факторной и остаточной сумм квадратов отклонений: 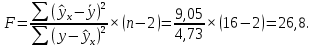 Определим критическое значение F-критерия используя таблицу распределения Фишера-Снедекора с учетом заданного уровня значимости 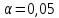 и числа степеней свободы и числа степеней свободы 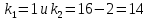 : :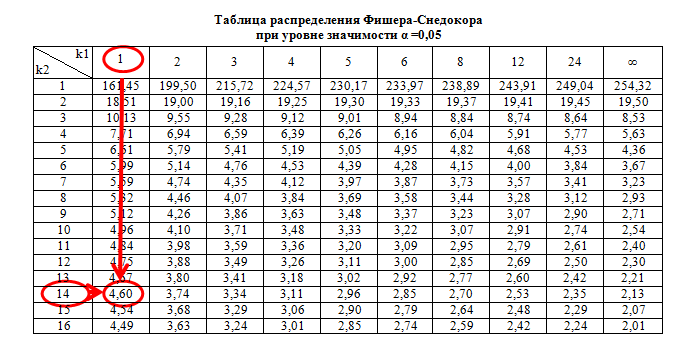 Табличное и фактическое значение F-критерия можно представить графически:  Рис.2.6.1. Подмножества значений F-критерия Рассчитанное по выборочным данным значение F-критерия равное 26,8 попадает в критическую область 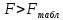 . Следовательно, нулевая гипотеза . Следовательно, нулевая гипотеза 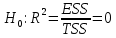 отвергается с вероятностью 95% (что равнозначно вероятности ошибки отвергается с вероятностью 95% (что равнозначно вероятности ошибки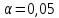 ). Это позволяет нам говорить о том, что связь между оборотом розничной торговли и доходами населения является неслучайной и построенное уравнение регрессии является статистически значимым. ). Это позволяет нам говорить о том, что связь между оборотом розничной торговли и доходами населения является неслучайной и построенное уравнение регрессии является статистически значимым.Табличное значение F-критерия можно получить используя функцию FРАСПОБР из категории «Статистические» в Microsoft Office Excel: 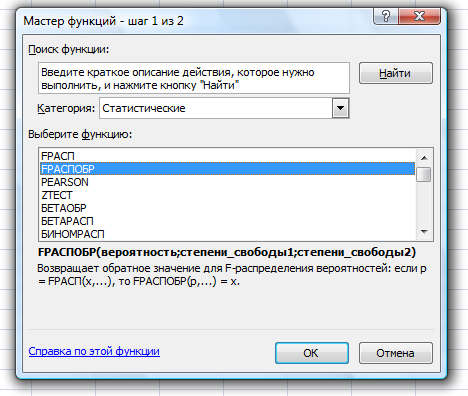 В диалоговом окне функции необходимо: в поле «Вероятность» - ввести уровень значимости (обычно 0,05 или 5%); в поле «Степени_свободы1» ввести число степеней свободы для объясненной суммы квадратов отклонений (в модели парной линейной регрессии – 1); в поле «Степени_свободы2» ввести число степеней свободы для остаточной суммы квадратов отклонений (в модели парной линейной регрессии – n-2, в нашем примере 16-2=14). 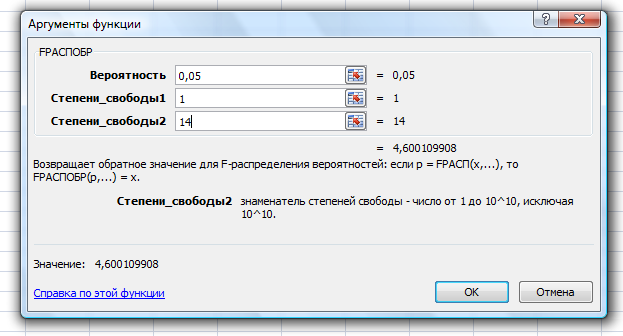 Полученное значение F-критерия равное 4,6 совпадает с тем значением, которое мы определили по таблице F-распределения. С помощью функции FРАСПР входящей в категорию «Статистические» Microsoft Office Excel возможно по рассчитанному значению F-критерия определить соответствующий ему уровень значимости 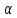 (р – значение): (р – значение):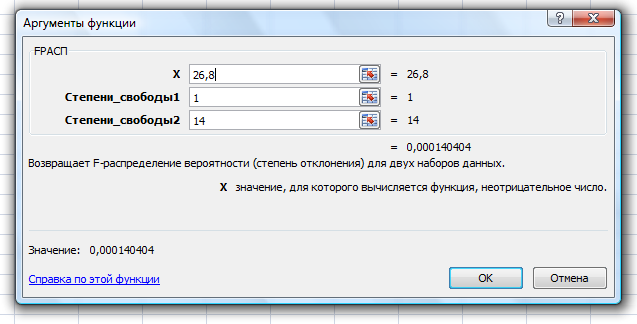 В диалоговом окне функции необходимо: в поле «Х» - ввести рассчитанное по выборочным данным значение F-критерия (в нашем примере 26,8); в поле «Степени_свободы1» ввести число степеней свободы для объясненной суммы квадратов отклонений (в модели парной линейной регрессии – 1); в поле «Степени_свободы2» ввести число степеней свободы для остаточной суммы квадратов отклонений (в модели парной линейной регрессии – n-2, в нашем примере 16-2=14). p-величина представляет собой накопленную вероятность наблюдения рассчитанного уровня статистического критерия при принятии нулевой гипотезы. Если p-значение меньше выбранного нами уровня значимости 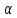 , то нулевая гипотеза отвергается. , то нулевая гипотеза отвергается.p-значение  говорит нам о том, что вероятность ошибки при отклонении нулевой гипотезы составляет говорит нам о том, что вероятность ошибки при отклонении нулевой гипотезы составляет 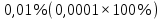 . Таким образом, вероятность того, что связь между оборотом торговли и доходами населения имеет неслучайный характер, составляет 99,99%. . Таким образом, вероятность того, что связь между оборотом торговли и доходами населения имеет неслучайный характер, составляет 99,99%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||