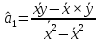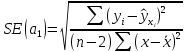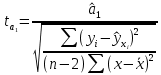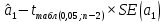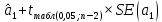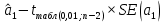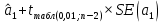Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Пример 2.10. В нашем примере: 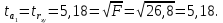 При этом p-величина для рассчитанных значений критериев 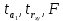 составила 0,0001 или 0,1%. составила 0,0001 или 0,1%.Поскольку t-критерий характеризует возможное отношение оценки параметра к его стандартной ошибке при заданном уровне значимости, табличное значение t-критерия можно построить использовать для построения доверительных интервалов параметров модели регрессии: 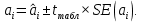 Тогда для модели парной линейной регрессии: 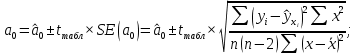 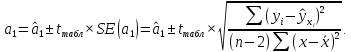 Пример 2.11. Рассчитаем интервальные оценки параметров модели регрессии оборота розничной торговли по величине доходов населения при уровне значимости 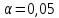 : :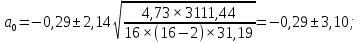 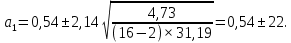 Таким образом, с вероятностью 95% можно утверждать, что значения параметров модели регрессии находятся в следующих пределах: 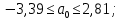  Если доверительный интервал параметра модели регрессии включает в себя нулевое значение, то это говорит о том, что гипотеза о статистической незначимости параметра не может быть отвергнута при заданном уровне значимости 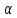 . . 7. Точечный и интервальный прогнозы для модели парной линейной регрессии Одной из задач эконометрического моделирования выступает прогнозирование социально-экономических явлений и процессов. Эта задача может решаться на основе регрессионных моделей, с помощью которых прогнозируется поведение результативной переменной в зависимости от поведения факторных переменных, включенных в модель. Точечный прогноз значения результативной переменной ( 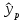 ) при заданном значение факторной переменной ( ) при заданном значение факторной переменной (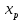 ) будет определяться по формуле: ) будет определяться по формуле: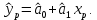 При этом действительная величина 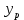 будет определяться как: будет определяться как: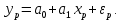 Таким образом, истинное значение результативной переменной будет отклоняться от расчетного значения под влиянием ошибок параметров модели и случайной ошибки регрессии. Запишем модель регрессии, используемую для прогнозирования, в следующем виде: 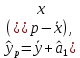 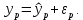 Отсюда следует, что стандартная ошибка регрессии 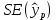 в точке в точке 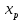 зависит от стандартной ошибки результативной переменной зависит от стандартной ошибки результативной переменной 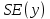 и стандартной ошибки коэффициента регрессии и стандартной ошибки коэффициента регрессии 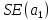 : :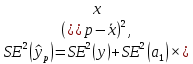 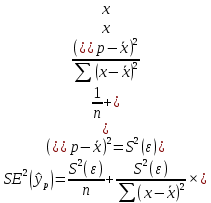 Теоретическое значение (математическое ожидание) результативной переменной в точке 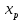 с вероятностью с вероятностью 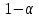 будет находиться в интервале, определяемом как: будет находиться в интервале, определяемом как: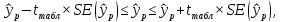 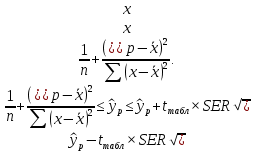 В свою очередь, ошибка истинного значения результативной переменой будет зависеть от ошибки регрессии в точке 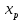 и дисперсии ошибок регрессии: и дисперсии ошибок регрессии: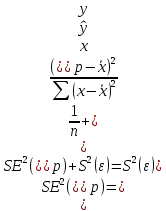 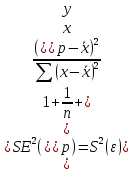 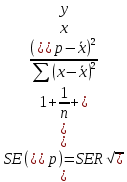 Таким образом, истинное значение результативной переменной в точке 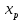 с вероятностью с вероятностью 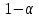 будет находиться в интервале, определяемом как: будет находиться в интервале, определяемом как: 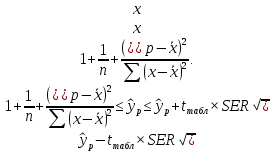 Другими словами 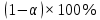 фактических значений результативной переменной в генеральной совокупности будут находиться в пределах указанного интервала. фактических значений результативной переменной в генеральной совокупности будут находиться в пределах указанного интервала. Из приведенных формул мы видим, что ошибка как теоретического, так и фактического значения результативной переменной зависят от трех параметров: Значение стандартной ошибки регрессии 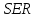 . Стандартная ошибка регрессии представляет собой корень из остаточной дисперсии на одну степень свободы. Следовательно, чем выше качество регрессионной модели, тем точнее сделанный по ней прогноз. . Стандартная ошибка регрессии представляет собой корень из остаточной дисперсии на одну степень свободы. Следовательно, чем выше качество регрессионной модели, тем точнее сделанный по ней прогноз.Отклонение точки 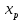 для которой рассчитывается прогнозное значение от среднего значения факторной переменной. Чем ближе для которой рассчитывается прогнозное значение от среднего значения факторной переменной. Чем ближе 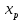 к к 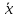 , тем точнее прогноз. Максимальная точность достигается в точке , тем точнее прогноз. Максимальная точность достигается в точке 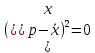 , то есть , то есть 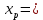 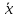 . .Дисперсии факторной переменной. Чем больше дисперсия xпри фиксированном числе наблюдений, тем точнее прогноз зависимой переменной. Пример 2.12. Рассмотрим пример нахождения доверительных интервалов для построенной нами модели парной линейной регрессии, описывающей зависимость оборота розничной торговли от доходов населения. Необходимо найти прогнозное значение оборота розничной торговли на душу населения в регионе, при заданной величине среднедушевых денежных доходов населения 15,6 тыс. руб. Занесем исходные данные в таблицу 2.7.1. Таблица 2.7.1 Исходные данные для прогнозирования оборота розничной торговли
Теоретическое значение оборота розничной торговли на душу населения при среднедушевых доходах населения в размере 15,6 тыс. руб. составит: 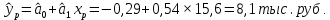 Найдем 95% доверительные интервалы для этого значения: 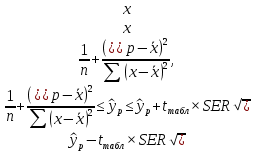 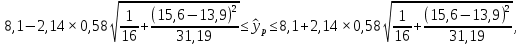  Таким образом, в 95% выборок (и соответственно в построенных по этим данным моделях регрессии) прогнозное значение оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб. будет находиться в пределах от 7,6 тыс. руб. до 8,5 тыс. руб. Определим 95% доверительные интервалы для фактического значения оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб.: 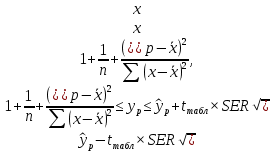 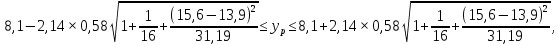 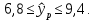 Следовательно, с вероятностью 0,95 мы можем утверждать, что фактическое значение оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб. будет находиться в пределах от 6,8 тыс. руб. до 9,4 тыс. руб. Рассмотрим графическое изображение найденных доверительных интервалов значений результативной переменной (рис. 2.7.1). 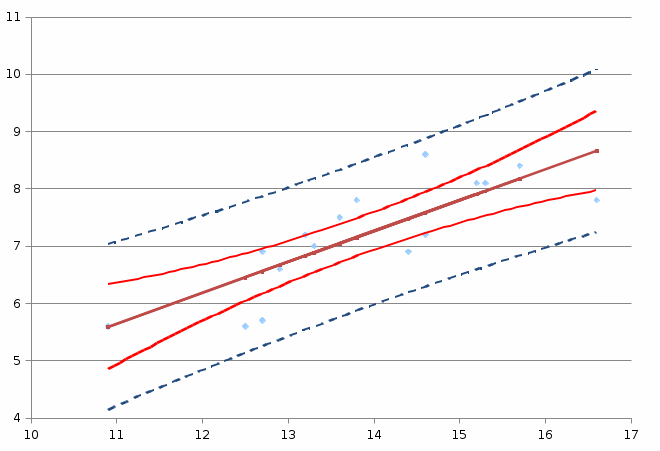 Линия регрессии   Доверительный интервал для линии регрессии    Рис. 2.7.1. Доверительные интервалы для теоретических и фактических значений результативной переменной (оборота розничной торговли на душу населения) На рисунке 2.6.1 мы видим, что границы доверительных интервалов расширяются по мере удаления от центра распределения факторной переменной. При этом все фактические значения оборота розничной торговли на душу населения попадают в 95% доверительный интервал. 8. Построение модели парной линейной регрессии средствами MS Office Excel Оценки параметров модели регрессии, а также показатели качества и статистической значимости модели можно рассчитать, используя возможности модуля «Анализ данных», входящего в блок надстроек «Пакет анализа». Для вызова команды «Анализ данных» необходимо нажать на соответствующую кнопку в меню «Данные»: 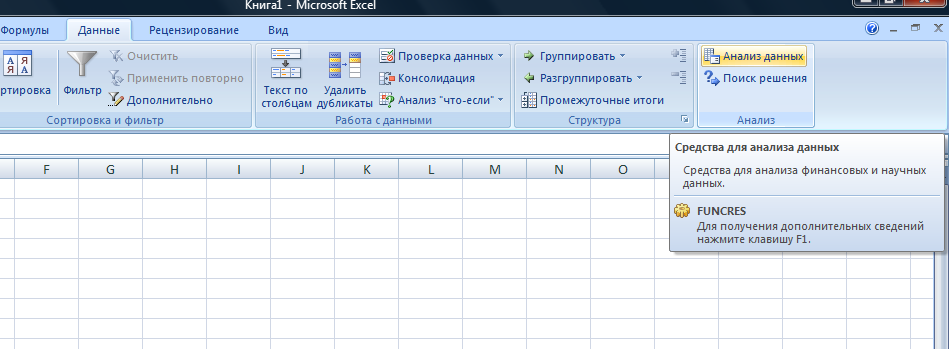  В меню «Анализ данных» необходимо выбрать инструмент анализа «Регрессия»: 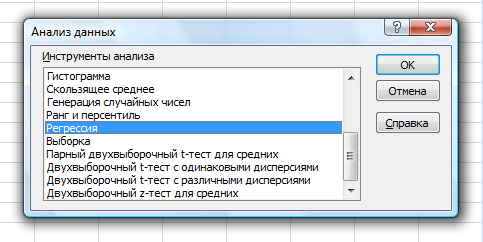 В диалоговом окне «Регрессия» возможно установить следующие параметры анализа: 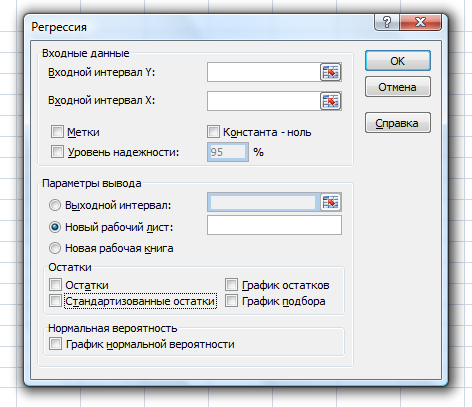 «Входной интервал Y» - ссылка на диапазон значений результативной переменной. Диапазон должен состоять из одного столбца. «Входной интервал X» - ссылка на диапазон значений факторной переменной. «Метки» - необходимо установить флажок, если выделенный диапазон содержит заголовки столбцов. «Уровень надежности» - необходимо установить флажок, если доверительные интервалы для параметров модели регрессии должны быть дополнительно рассчитаны для вероятности отличной от 95%, применяемой по умолчанию. Обычно используют уровень надежности 99% для проверки нулевых гипотез при уровне значимости 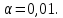 «Константа – ноль» - необходимо установить флажок, если теоретическое обоснование модели предполагает 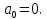 «Параметры вывода» - необходимо выбрать расположение таблицы с результатами регрессионного анализа. «Остатки» - при установке флажка в результаты регрессии будут включены значения регрессионных остатков. «Стандартизированные остатки» - при установке флажка в результаты регрессии будут включены стандартизированные значения регрессионных остатков (со средней равной 0 и дисперсией равной 1). «График остатков» - при установке флажка будет показана диаграмма рассеяния для значений регрессионных остатков и факторной переменной. Данный график используется для визуальной проверки предпосылок МНК о гомоскедастичности остатков и экзогенности факторной переменной. «График подбора» - при установке флажка будет показан график зависимости фактических и теоретических значений результативной переменной. Данный график используется для визуальной оценки качества построенной модели. «График нормальной вероятности» - при установке флажка будут показаны таблица и график распределения результативной переменной. Пример 2.13. Проведем анализ данных, характеризующих среднедушевые денежные доходы населения и среднемесячный оборот розничной торговли на душу населения регионов Центрального федерального округа Российской Федерации за 2010 г. с использованием инструмента «Регрессия» пакета анализа MSOfficeExcel: 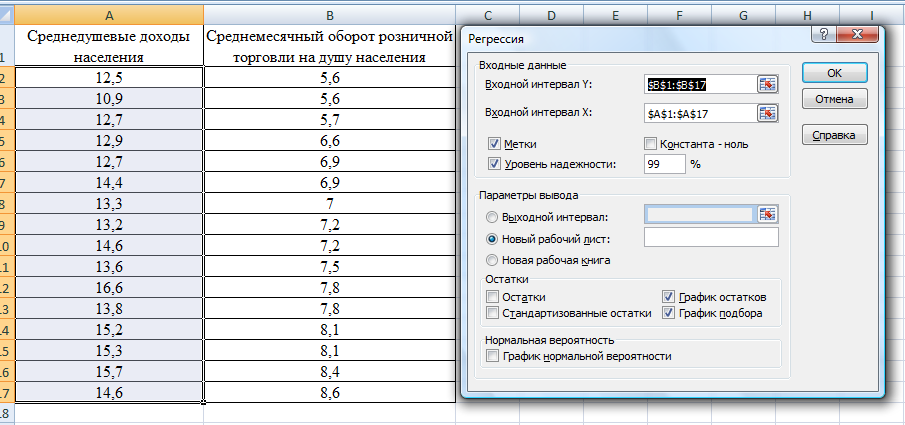 Полученная в результате использования инструмента «Регрессия» таблица «Вывод итогов» состоит из следующих элементов: Таблица «Регрессионная статистика»
Для модели парной линейной регрессии доступна интерпретация следующих показателей:
Таблица «Дисперсионный анализ»
Для модели парной линейной регрессии доступна интерпретация всех показателей:
Таблица «Оценка параметров»
Для модели парной линейной регрессии доступна интерпретация всех показателей:
Значения показателей, полученные с использованием инструмента «Регрессия» пакета анализа MSOfficeExcelсовпадают со значениями, полученными нами ранее при самостоятельных расчетах, с учетом ошибок округления. Рассмотрим графики, построенные с использованием инструмента «Регрессия» пакета анализа MSOfficeExcel: График остатков: 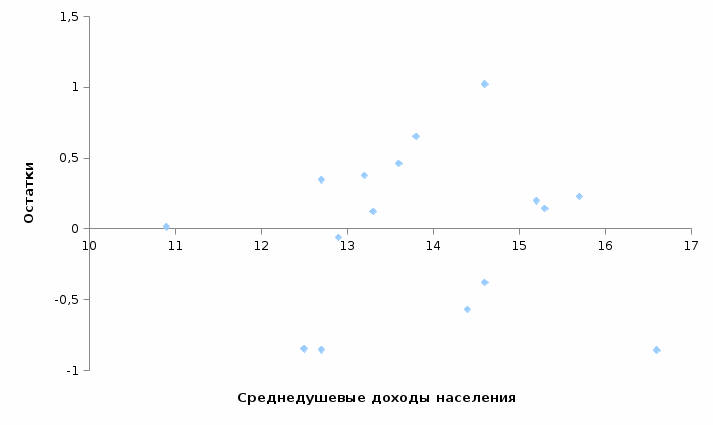 Рис. 2.8.1. График остатков модели регрессии оборота розничной торговли на душу населения по величине среднедушевых денежных доходов населения Вид графика остатков говорит нам о том, что: - величина остатков равномерно распределена вокруг нулевого среднего значения (то есть остатки гомоскедастичны); - значения остатков не зависят от значений факторной переменной. График подбора: 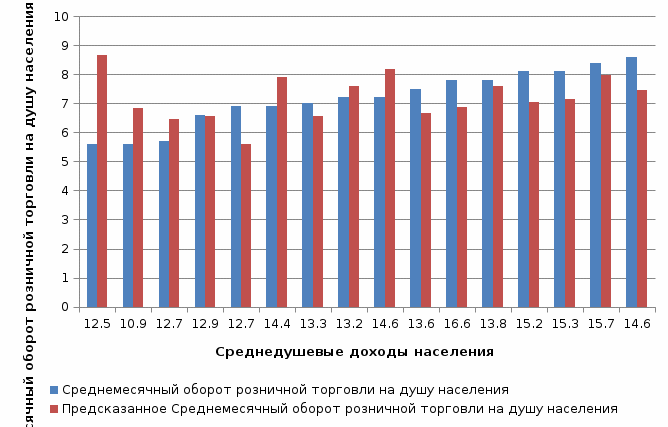 Рис. 2.8.2. График наблюдаемых и предсказанных значений оборота розничной торговли на душу населения Вид графика подбора говорит нам о том, что: - расчетные (предсказанные) значения результативной переменой незначительно отличаются от фактических (наблюдаемых) значений; - значения остатков (разность между столбцами) не зависят от значений факторной переменной. Ранее мы говорили о том, что для корректного использования параметрических критериев и построения доверительных интервалов необходимо, чтобы ошибки регрессии подчинялись нормальному распределению. Для проверки соблюдения данной предпосылки оценивают гипотезу о нормальном распределении регрессионных остатков. При этом обычно используют критерии согласия Пирсона, Колмогорова-Смирнова и др. Однако использование указанных критериев сопряжено с трудностями вычислений, при отсутствии специализированного программного обеспечения. Этого недостатка лишен тест Жарка-Бера при помощи которого проверяется гипотеза вида: 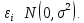 Если нулевая гипотеза верна, то величина: 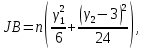 имеет распределение 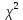 с числом степеней свободы равным 2. с числом степеней свободы равным 2.Величину 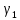 называют коэффициентом асимметрии и рассчитывают как: называют коэффициентом асимметрии и рассчитывают как: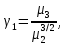 где 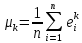 – центральный момент регрессионных остатков порядка k. – центральный момент регрессионных остатков порядка k.Величину 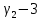 называют коэффициентом эксцесса и рассчитывают как: называют коэффициентом эксцесса и рассчитывают как: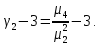 Пример 2. 14. Используем тест Жарка-Бера для проверки гипотезы о нормальном распределении остатков модели регрессии оборота розничной торговли по доходам населения. Значения регрессионных остатков получим при использовании инструмента «Регрессия» модуля «Анализ данных» MSOfficeExcel, установив флажок «Остатки». Значения коэффициентов асимметрии и эксцесса определим используя инструмент «Описательная статистика» модуля «Анализ данных» MSOfficeExcel: 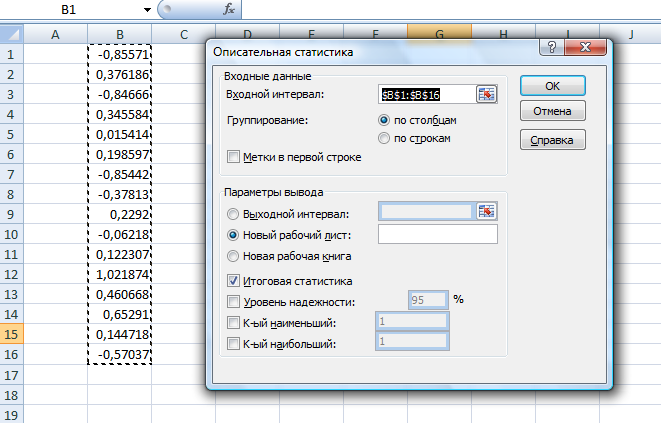 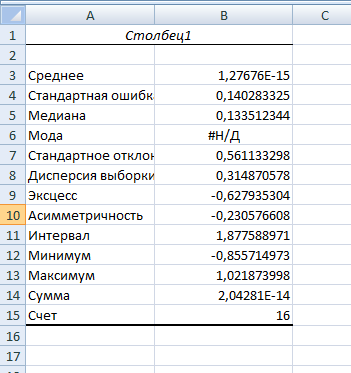  Коэффициент асимметрии  Коэффициент эксцесса Рассчитаем значение статистики Жарка-Бера: 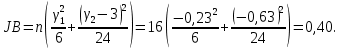 Табличное значение распределения 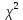 с числом степеней свободы равным 2 при уровне значимости с числом степеней свободы равным 2 при уровне значимости 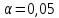 определим используя формулу «ХИ2ОБР» MSOfficeExcel: определим используя формулу «ХИ2ОБР» MSOfficeExcel: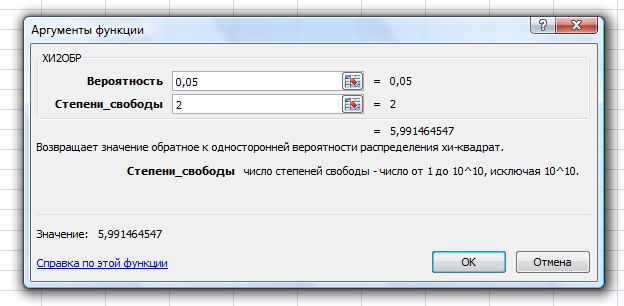 Поскольку 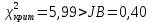 нулевая гипотеза о нормальном распределении ошибки регрессии не может быть отвергнута при заданном уровне значимости. нулевая гипотеза о нормальном распределении ошибки регрессии не может быть отвергнута при заданном уровне значимости.Следовательно, использование нами для оценки статистической значимости модели регрессии распределений Фишера и Стьюдента является корректным. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

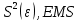
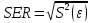
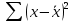
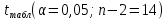
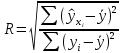
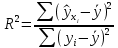
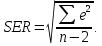
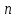
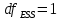
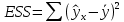
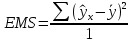
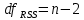
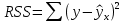
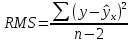
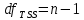
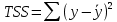
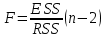
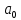 , свободный член
, свободный член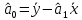
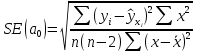
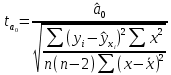
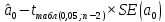
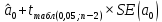
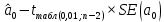
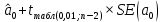
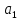 , коэффициент регрессии
, коэффициент регрессии