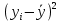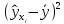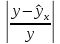Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Наилучшей называют оценку параметра в том случае, если она имеет наименьшую дисперсию из всех возможных оценок. В этом же состоит и свойство эффективности. То есть если оценка параметра является наилучшей, то она является эффективной. Следует пояснить, что под дисперсией оценки параметра мы понимаем средний квадрат отклонений различных оценок данного параметра, полученных для различных выборок, от истинного значения параметра в генеральной совокупности. Дисперсия МНК-оценки параметра 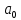 определяется по формуле: определяется по формуле: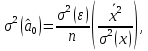 где  - дисперсия случайной ошибки; - дисперсия случайной ошибки;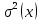 - дисперсия фактора x. - дисперсия фактора x.Однако генеральная дисперсия случайной ошибки  является неизвестной величиной, что обуславливает необходимость получения ее выборочной оценки является неизвестной величиной, что обуславливает необходимость получения ее выборочной оценки 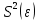 (исправленной дисперсии): (исправленной дисперсии):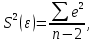 где 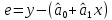 – регрессионные остатки. – регрессионные остатки.Стандартная ошибка регрессии (SER, StandardErrorofRegression) при этом будет рассчитываться по формуле: 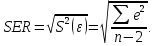 Таким образом, следует различать ошибку регрессии (Error, ε), которая является неизвестной случайной величиной, и регрессионный остаток (Residual, e), рассчитываемый на основе известных оценок параметров модели: 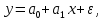 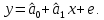 Значение знаменателя формулы оценки дисперсии случайной ошибки равное n-2 обусловлено тем, что по выборке объемом n единиц мы оцениваем два параметра 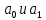 . .Учитывая вышесказанное, формулу для оценки дисперсии МНК-оценки параметра 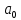 мы можем представить в следующем виде: мы можем представить в следующем виде: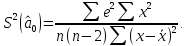 Дисперсия МНК-оценки параметра 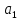 определяется по формуле: определяется по формуле: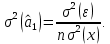 В свою очередь оценка дисперсии МНК-оценки параметра 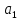 определяется по формуле: определяется по формуле: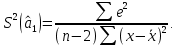 Оценка параметра является линейной если она находится в линейной функциональной зависимости от выборочных данных. На практике это означает что зависимость между исследуемыми переменными имеет линейный вид. Оценка параметра является несмещенной если ее выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности:  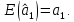 Другими словами оценка параметра является несмещенной если при любом объеме выборки, результат ее осреднения по всем возможным выборкам такого же объема равен истинному значению оцениваемого параметра в генеральной совокупности. Оценка параметра является состоятельной если при увеличении объема выборки значение оценки стремится к значению оцениваемого параметра генеральной совокупности, то есть для сколь угодно малой положительной величины  вероятность вероятность 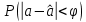 стремиться к нулю при увеличении объема выборки n: стремиться к нулю при увеличении объема выборки n: 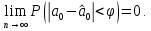 Таким образом, состоятельная оценка параметра модели регрессии удовлетворяет закону больших чисел. 4. Предпосылки МНК при оценивании параметров модели регрессии Для того чтобы оценки параметров модели регрессии полученные с использованием МНК обладали свойствами состоятельности, эффективности и несмещенности необходимо соблюдение ряда предпосылок или допущений МНК. Первые предпосылки формулируются относительно природы исходных данных: Истинная форма зависимости между результатирующей переменной y и факторной переменной x является линейной. Факторная переменная x является нестохастической (неслучайной), то есть в анализе используется фиксированный набор ее значений. Предположение о нестохастической природе факторной переменной означает, что в ходе контролируемого эксперимента при одном и том же наборе значений переменной xбудут получены различные наборы значений случайной ошибки 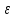 и, следовательно, различные наборы значений результативной переменной y. и, следовательно, различные наборы значений результативной переменной y. На практике нарушение предпосылки о нестохастической природе факторной переменной чаще всего возникает в ходе проведения статистического наблюдения за исследуемыми переменными. Рассмотрим ситуацию, когда переменная x является стохастической переменной вследствие возникновения ошибки наблюдения 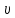 . Пусть наблюдаемое значение факторной переменной xскладывается из истинного значения исследуемого признака . Пусть наблюдаемое значение факторной переменной xскладывается из истинного значения исследуемого признака  и ошибки измерения и ошибки измерения 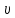 : : тогда тогда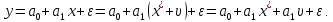 В силу тождества 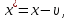 между x*и между x*и 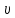 существуетзависимость, что делает МНК-оценки параметров рассмотренной модели смещенными и несостоятельными. Причины этого явления будут рассмотрены нами в разделе посвященном изучению проблемы мультиколлинеарности. существуетзависимость, что делает МНК-оценки параметров рассмотренной модели смещенными и несостоятельными. Причины этого явления будут рассмотрены нами в разделе посвященном изучению проблемы мультиколлинеарности.Вторая группа предпосылок МНК формулируется относительно свойств случайных ошибок модели регрессии: 1. Математическое ожидание (средняя величина) случайных ошибок модели регрессии равно 0: 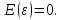 Для модели регрессии содержащей свободный член данная предпосылка никогда не нарушается. Если теоретическое обоснование модели требует приравнивания свободного члена к нулю, то есть перехода к регрессионной модели вида 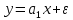 , то несоблюдение рассматриваемой предпосылки ведет к существенному смещению оценки параметра , то несоблюдение рассматриваемой предпосылки ведет к существенному смещению оценки параметра 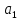 . .Дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений: 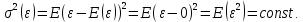 Учитывая, что регрессионные остатки представляют собой выборочные оценки случайной ошибки модели, говорят о гомоскедастичных остатках или гомоскедастичности, когда остатки имеют одинаковую дисперсию, и о гетероскедастичных остатках или гетероскедастичности – когда дисперсия остатков различна. Примеры отображения гетероскедастичных и гомосскедастичных остатков на диаграмме рассеяния представлены на рисунке 2.4.1. 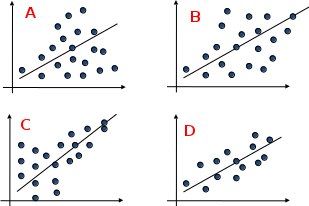 Рис. Примеры гетероскедастичности (A-C) и гомоскедастичности (D) остатков Гетероскедастичность остатков ведет к смещению стандартных ошибок параметров модели регрессии, что затрудняет проверку их статистической значимости. 3. Ковариация между значениями случайной ошибки для любой пары наблюдений равна 0: 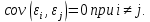 Нарушение данной предпосылки называют автокорреляцией случайной ошибки или автокорреляцией остатков. Данная проблема возникает при построении моделей регрессии по данным, представленным в виде временных рядов. Автокорреляция остатков, как и их гетероскедастичность обуславливает смещение стандартных ошибок параметров модели регрессии. 4. Случайная ошибка 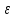 и факторная переменная x независимы друг от друга: и факторная переменная x независимы друг от друга: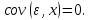 Данная предпосылка представляет собой частный случай допущения о нестохастической природе факторной переменной. В случае несоблюдения предпосылки говорят о проблеме эндогенности. При этом МНК-оценки параметров регрессии являются несостоятельными и смещенными: 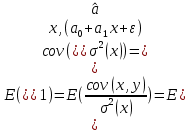 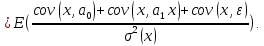 Учитывая, что 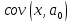 =0, =0, 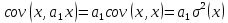 получим: получим: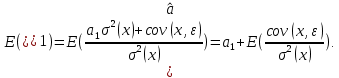 Таким образом при 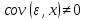 , а следовательно , а следовательно 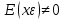 не выполняется условие несмещенности оценки параметра не выполняется условие несмещенности оценки параметра 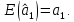 5. Оценка качества модели парной линейной регрессии Качеством регрессионной модели называется адекватность построенной модели исходным данным. Для оценки качества модели регрессии используют следующие показатели: Линейный коэффициент корреляции: 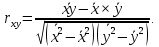 Как уже отмечалось ранее, этот коэффициент характеризует тесноту и направление связи между исследуемыми переменными. Расчет линейного коэффициента парной корреляции можно осуществить на основе использования оценки коэффициента регрессии:  Средняя ошибка аппроксимации: 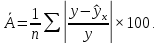 Средняя ошибка аппроксимации показывает на сколько процентов в среднем расчетные (теоретические) значения результативной переменной у отклоняются от ее фактических значений. Коэффициент детерминации. Расчет коэффициента детерминации основан на декомпозиции отклонений результативной переменной y, пример которой приведен на рисунке 2.5.1. Согласно проведенной декомпозиции, отклонение фактических значений результативной переменной от теоретических можно представить в следующем виде: 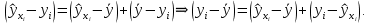 Разность 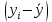 называют общим отклонением, поскольку она полностью описывает вариацию результативной переменной. Разность называют общим отклонением, поскольку она полностью описывает вариацию результативной переменной. Разность  называют объясненным отклонением, поскольку его значение можно объяснить исходя из модели регрессии. Действительно, поскольку называют объясненным отклонением, поскольку его значение можно объяснить исходя из модели регрессии. Действительно, поскольку  является постоянной величиной мы можем найти значение объясненного отклонения зная только параметры модели регрессии и изменение фактора является постоянной величиной мы можем найти значение объясненного отклонения зная только параметры модели регрессии и изменение фактора  . Разность . Разность 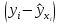 называют необъясненным отклонением в силу того, что его значение невозможно объяснить располагая лишь моделью регрессии. называют необъясненным отклонением в силу того, что его значение невозможно объяснить располагая лишь моделью регрессии. 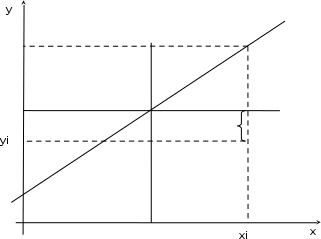 Рис. 2.5.1. Декомпозиция отклонений результативной переменной Таким образом, общее отклонение 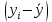 характеризующее изменение результативной переменной под влиянием всех возможных факторов разлагается на объясненное или факторное отклонение характеризующее изменение результативной переменной под влиянием всех возможных факторов разлагается на объясненное или факторное отклонение  характеризующее вариацию результативной переменной под влиянием факторов, включенных в модель регрессии, и необъясненное или остаточное отклонение характеризующее вариацию результативной переменной под влиянием факторов, включенных в модель регрессии, и необъясненное или остаточное отклонение 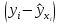 характеризующее вариацию результативной переменной под влиянием всех факторов не включенных в регрессионную модель. характеризующее вариацию результативной переменной под влиянием всех факторов не включенных в регрессионную модель.Возведя в квадрат и просуммировав элементы равенства отклонений и учитывая, что 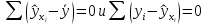 получим: получим: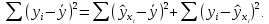 Данное выражение обычно называют разложением общей суммы квадратов отклонений результативной переменной от среднего значения и записывают в следующем виде: 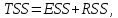 где  - общая сумма квадратов отклонений результативной переменной от среднего значения; - общая сумма квадратов отклонений результативной переменной от среднего значения;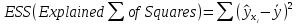 – объясненная (факторная) сумма квадратов отклонений; – объясненная (факторная) сумма квадратов отклонений;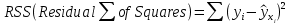 – остаточная сумма квадратов отклонений. – остаточная сумма квадратов отклонений.Коэффициентом детерминации ( 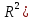 называют отношение объясненной суммы квадратов отклонений к общей: называют отношение объясненной суммы квадратов отклонений к общей: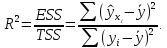  Коэффициент детерминации характеризует долю вариации результативной переменной y объясняемую вариацией факторов X включенных в регрессионную модель. В силу того, что 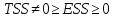 значение коэффициента детерминации находятся в пределах от 0 до 1 или от 0 до 100%. Причем если значение коэффициента детерминации находятся в пределах от 0 до 1 или от 0 до 100%. Причем если 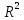 – доля вариации результативной переменной объясняемая вариацией факторов включенных в модель, то – доля вариации результативной переменной объясняемая вариацией факторов включенных в модель, то 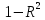 – доля вариации результативной переменной объясняемая вариацией факторов, не включенных в модель. – доля вариации результативной переменной объясняемая вариацией факторов, не включенных в модель.В линейных регрессионных моделях коэффициент детерминации численно равен квадрату линейного коэффициента корреляции: 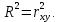 Пример 2.6. Рассчитаем показатели качества модели регрессии, построенной по данным характеризующим оборот розничной торговли и среднедушевые денежные доходы населения Центрального федерального округа. Таблица 2.5.1 Данные для показателей качества модели парной линейной регрессии оборота розничной торговли по величине денежных доходов населения
В соответствии с данными, приведенными в таблице: 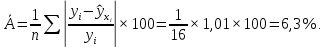 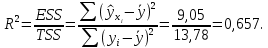 Таким образом, расчетные значения оборота розничной торговли в среднем отличаются от фактических значений на 6,3%. Вариация оборота розничной торговли на 65,7% (  объясняется вариацией доходов населения, а на 34,3% ( объясняется вариацией доходов населения, а на 34,3% (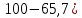 - вариацией прочих факторов, не включенных в модель. - вариацией прочих факторов, не включенных в модель. |