Тема Модель парной линейной регрессии Понятие регрессии. Спецификация модели регрессии
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Если линейный коэффициент корреляции принимает абсолютное значение равное 1, то это свидетельствует о том, что между исследуемыми переменными существует линейная функциональная связь: 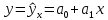 . .Пример 2.2. Покажем пример расчета линейного коэффициента на основе данных, приведенных в таблице 2.1.1. Для удобства дополним эту таблицу расчетными строками и графами (таблица 2.2.2). Таблица 2.1.2 Данные для расчета линейного коэффициента корреляции между денежными доходами населения и оборотом розничной торговли на душу населения регионов центрального федерального округа Российской Федерации за 2010 г.
 . .Значение линейного коэффициента корреляции можно рассчитать, используя встроенную функцию «КОРЕЛЛ» Microsoft Office Excel: Шаг 1. Открываем «Мастер функций» нажав кнопку fxв строке формул:   или нажав на кнопку «Вставить функцию» на вкладке «Формулы»:  Шаг 2. В диалоговом окне «Мастер функций» выбрать функцию «КОРРЕЛ» из категории «Статистические»:  В диалоговом окне «Аргументы функции» указать ссылки на столбцы с исходными данными: 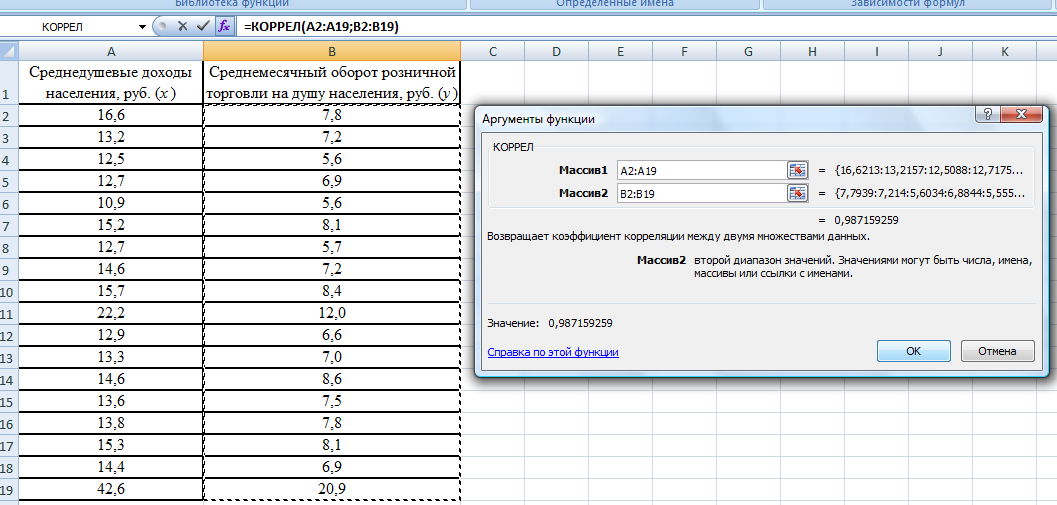 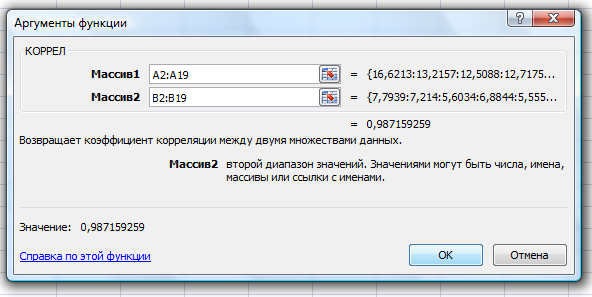 Полученное значение линейного коэффициента корреляции равное 0,987 совпадает с результатом наших самостоятельных расчетов. Оно свидетельствует о том, что между денежными доходами населения и оборотом розничной торговли на душу населения существует линейная прямая очень тесная связь. Зная как рассчитывается линейный коэффициент корреляции, мы можем рассмотреть примеры того, как взаимосвязаны его значения и вид поля корреляции, построенного по тем же данным. Во-первых, чем тесней точки поля корреляции сгруппированы относительно воображаемой прямой, тем выше теснота связи и, следовательно, больше абсолютное значение коэффициента корреляции. Если все точки расположены точно на одной прямой, то наблюдается линейная функциональная связь и модуль коэффициента корреляции равен 1. Примеры того, как выглядит поле корреляции при различных значениях линейного коэффициента корреляции представлены на рисунке 2.1.5. 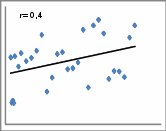 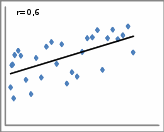 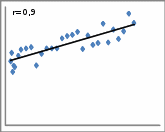 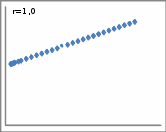 Рис. 2.1.5. Поле корреляции при различных значениях коэффициента корреляции Во-вторых, следует помнить, что при помощи линейного коэффициента корреляции можно оценить тесноту только линейной связи. Если связь не линейна, этот коэффициент не может адекватно измерить ее тесноту. Вернемся к рисунку 2.1.2. Если на основе представленного распределения мы рассчитаем линейный коэффициент корреляции, то его значение равное 0,23 свидетельствует, по шкале Чеддока, о слабой связи между переменными. Это утверждение ошибочно. Чтобы убедиться в этом, нанесем на график прямую линию, проходящую вдоль точек графика (рис. 2.1.6.). Мы видим, что точки графика нельзя упорядочить относительно прямой, однако они легко упорядочиваются вокруг параболы. Таким образом, связь между исследуемыми переменными есть, она достаточно тесная, но не линейная. 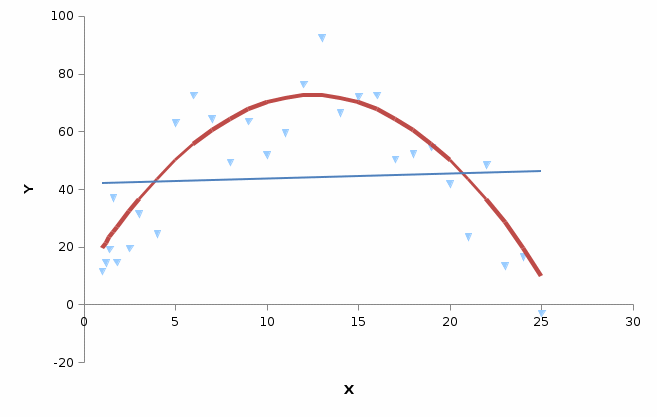 Рис. 2.1.6. Выбор между прямой и параболой при описании тесноты связи В-третьих, на значения коэффициента корреляции существенное влияние оказывают выбросы, наглядное изображение которых можно увидеть на поле корреляции. Выбросы – это результаты наблюдений, выделяющиеся из рассматриваемой совокупности или не попадающие под общее распределение. Пример 2.3. Рассмотрим вновь поле корреляции оборота розничной торговли на душу населения и величины среднедушевых денежных доходов населения регионов центрального федерального округа (рис. 2.1.7). 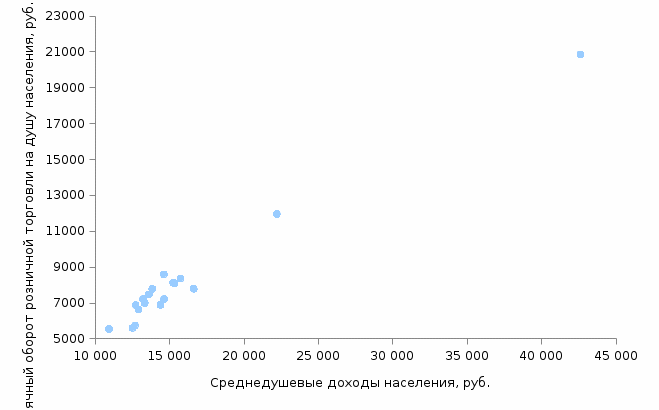 Рис. 2.1.7. Поле корреляции (диаграмма рассеяния) оборота розничной торговли на душу населения и величины среднедушевых денежных доходов населения На рисунке мы видим, что два региона (Московская область и г. Москва) по своим характеристикам заметно отличаются от остальных. Посмотрим, как выглядело бы поле корреляции при устранении указанных наблюдений из анализируемой совокупности (рис. 2.1.8). 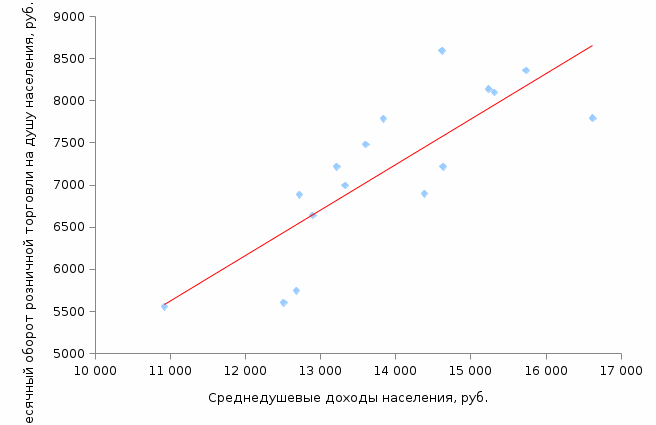 Рис. 2.1.8. Поле корреляции (диаграмма рассеяния) оборота розничной торговли на душу населения и величины среднедушевых денежных доходов населения с учетом устранения выбросов Устранение выбросов существенно изменило вид поля корреляции. Между доходами населения и оборотом розничной торговли по прежнему наблюдается прямая линейная связь, однако судя по разбросу точек вокруг воображаемой прямой ее теснота уменьшилась. Проверим это, рассчитав линейный коэффициент корреляции. Действительно, значение коэффициента уменьшилось с 0,99 до 0,82, что соответствует о тесной связи по шкале Чеддока, против очень тесной, наблюдавшейся до устранения выбросов. Наиболее простым, и в то же время действенным методом анализа выбросов является использование квартильного размаха (межквартильного расстояния). При этом экстремальными выбросами считаются наблюдения большие величины Q3+3IQR или меньшие величины Q1-3IQR, где IQR = Q3-Q1 – квартильный размах; Q3 – третий квартиль распределения исследуемой переменной; Q1 – первый квартиль распределения исследуемой переменной. В свою очередь умеренные выбросы заключены в диапазоны (Q3+1,5IQR,Q3+3IQR)и(Q1-1,5IQR,Q1-3IQR). Следовательно наблюдения не являющиеся выбросами будут находиться в интервале (Q1-1,5IQR,Q3+1,5IQR). Достоинством данного метода является робастность (то есть действенность в условиях наличия выбросов) показателей первого и третьего квартилей. Это проявляется в том, что численные характеристики приведенного правила оценки выбросов, рассчитываемые по исследуемой совокупности, не зависят от наличия в ней выбросов. Применим приведенные формулы к данным нашего примера, установив тем самым правомерность удаления двух регионов из анализируемой совокупности. Для расчета структурных характеристик (первый и третий квартили) каждой из совокупностей значений переменных x и y воспользуемся встроенной функцией «КВАРТИЛЬ» Microsoft Office Excel, находящейся в категории «Статистические функции»: 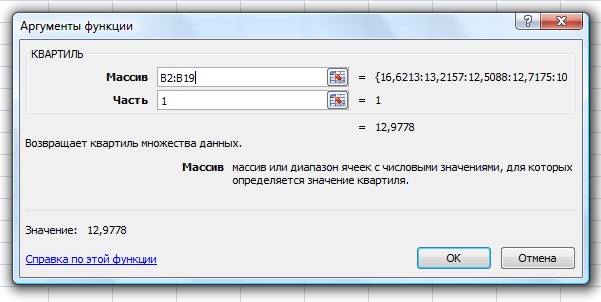 В строке «Массив» необходимо указать ссылку на столбец с анализируемыми данными, в строке «Часть» необходимо указать аргумент «1» для расчета первого квартиля и аргумент «3» для расчета третьего квартиля. Результаты расчетов представлены в таблице 2.1.3. Таблица 2.1.3 Структурные характеристики распределения регионов центрального федерального округа по величине денежных доходов населения и обороту розничной торговли на душу населения в 2010 г.
Согласно данным приведенным в таблице к экстремальным выбросам следует отнести регионы со среднедушевыми доходами населения большими чем 22,2 тыс. руб. или меньшими чем 6,1 тыс. руб. Следовательно, к экстремальным выбросам по величине доходов населения мы относим два отмеченных нами региона – г. Москву (42591,8 руб.) и Московскую область (22200,1 руб.). Соответственно умеренными выбросами будут являться регионы, в которых значения среднедушевых доходов будут находиться в интервалах (18,8;22,2)и (6,0;9,5) тыс. руб. В исследуемой совокупности таких регионов нет. К экстремальным выбросам по величине оборота розничной торговли на душу населения следует отнести регионы в которых значение данного показателя превышает 11,8 тыс. руб. или находится ниже отметки в 3,2 тыс. руб. Как и в случае с величиной доходов населения к экстремальным выбросам мы относим г. Москву (20868,8 руб.) и Московскую область (11964,9руб.). Умеренными выбросами будут являться регионы, в которых значения оборота торговли на душу населения будут находиться в интервалах (10,0;11,8)и (3,2;5,0) тыс. руб. В исследуемой совокупности таких регионов нет. Таким образом, проведенный анализ подтвердил правоверность исключения из рассматриваемой совокупности двух наблюдений, установленных при визуальном анализе поля корреляции. Удобным инструментом анализа выбросов являются графики «Box&Whiskers Plot». Дословный перевод этого термина означает «Ящик с усами», наиболее приближенным по смыслу переводом является «Коробковая диаграмма». Покажем построение этого графика средствами Microsoft Office Excel. Шаг 1. Сформируем таблицу с границами интервалов выбросов в следующем порядке:
Шаг 2. Выделим все ячейки сформированной таблицы, после чего на вкладке «Вставка» выберем в категории «Диаграммы», подкатегории «Биржевые» вид диаграммы «Открытие-максимальный-минимальный-закрытие». Полученный график имеет вид (рис. 2.1.9): 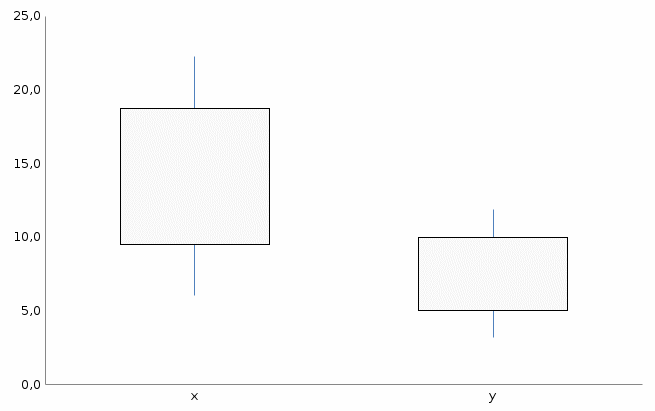 Рис. 2.1.9. Коробковая диаграмма распределения доходов населения и оборота розничной торговли Полученный график интерпретируют следующим образом. Наблюдения попадающие в «ящик» не являются выбросами. Наблюдения расположенные на «усах» представляют собой умеренные выбросы. И наконец наблюдения выходящие за пределы усов представляют собой экстремальные выбросы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
