Главная страница
Навигация по странице:

  • Свойство биссектрисы угла

  • Окружность, описанная около треугольника

  • Признаки равнобедренного треугольника

    		•

    геометрия. Сумма углов многоугольника


    Скачать 56.54 Kb.
    НазваниеСумма углов многоугольника
    Дата08.02.2018
    Размер56.54 Kb.
    Формат файлаdocx
    Имя файлагеометрия.docx
    ТипДокументы
    #36100

    Сумма углов многоугольника

    Теорема

    (о сумме углов выпуклого многоугольника)

    Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

    (n — количество сторон многоугольника).

    Другой вариант формулировки этой теоремы:

    Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

    Дано: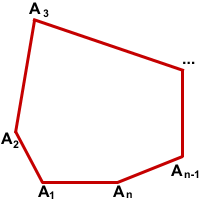summa-uglov-mnogougolnika

    \[{a_1}{a_2}{a_3}...{a_{n - 1}}{a_n}\] — выпуклый n -угольник.

    Доказать: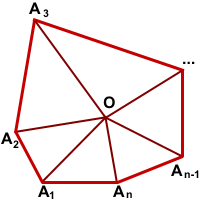

    \[\angle {a_1} + \angle {a_2} + \angle {a_3} + ... + \angle {a_{n - 1}} + \angle {a_n} = \] \[ = {180^o}(n - 2)\]

    summa-uglov-n-ugolnika

    Доказательство:

    1-й способ

    Обозначим внутри многоугольника произвольную точку O.

    Соединим точку O с вершинами многоугольника.

    Получили n треугольников.

    \[\angle {a_1} + \angle {a_2} + \angle {a_3} + ... + \angle {a_{n - 1}} + \angle {a_n} = \]\[ + \angle o{a_{n - 1}}{a_n} + \angle o{a_n}{a_{n - 1}}.\]

      Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O. Так как сумма углов при вершине O составляет 360º\[ = \angle o{a_1}{a_2} + \angle o{a_2}{a_1} + ... + \]

    \[\angle {a_1}o{a_2} + \angle {a_2}o{a_3} + ... + \angle {a_{n - 1}}o{a_n} = {360^o},\]

    то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

    Сумма углов каждого треугольника равна 180º.

    Таким образом, искомая сумма углов n угольника равна

    Что и требовалось доказать. \[ = {180^o} \cdot 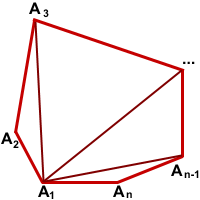n - {360^o} = {180^o}(n - 2).\]\[\angle {a_1} + \angle {a_2} + \angle {a_3} + ... + \angle {a_{n - 1}} + \angle {a_n} = \]

    2-й способteorema-o-summe-uglov-mnogougolnika

    Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

    Сумма всех углов этих треугольников равна сумме углов многоугольника.

    Сумма углов углов каждого из треугольников равна 180º.

    Следовательно, сумма углов многоугольника

    \[ = {180^o}(n - 2).\]\[\angle {a_1} + \angle {a_2} + \angle {a_3} + ... + \angle {a_{n - 1}} + \angle {a_n} = \]

    Что и требовалось доказать.

    Свойство биссектрисы угла

    Любая точка биссектрисы неразвёрнутого угла равноудалена от сторон этого угла.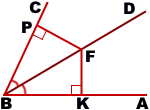svojstvo-bissektrisy-ugla

    Дано: BD — биссектриса ∠ABC, F∈BD,

    \[fk \bot ab,fp \bot bc\]

    Доказать: FK=FP

    Доказательство:

    Рассмотрим треугольники BFK и BFP.

    ∠BKF=∠BPF=90º, ∠KBF=∠PBF (так как по условию BD — биссектриса ∠ABC).

    BF — общая сторона.

    Значит, ∆BFK=∆BFP (по гипотенузе и острому углу).

    Из равенства треугольников следует равенство соответствующих сторон: FK=FP.

    Что и требовалось доказать.

    Обратно:

    Любая точка внутри неразвёрнутого угла, равноудалённая от сторон этого угла, лежит на его биссектрисе.

    Треугольники BFK и BFP в этом случае равны по катету и гипотенузе (FK=FP по условию, BF — общая сторона). Из равенства треугольников следует равенство соответствующих углов:∠KBF=∠PBF, а значит, BD — биссектриса ∠ABC.

    Окружность, описанная около треугольника

    Что такое окружность, описанная около треугольника? Что является центром этой окружности? Как расположение центра описанной окружности зависит от вида треугольника?

    Определение.

    Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.

    При этом треугольник называется вписанным в окружность.

    Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.okruzhnost, opisannaya okolo treugolnika

    Окружность можно описать около любого треугольника.

    Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).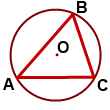okruzhnost, opisannaya okolo ostrougolnogo treugolnika

    Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.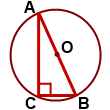

    okruzhnost, opisannaya okolo pryamougolnogo treugolnika

    Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.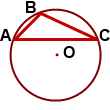

    okruzhnost, opisannaya okolo tupougolnogo treugolnika

    Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной).

    Признаки равнобедренного треугольника:

    • если в треугольнике два угла равны, то он равнобедренный;

    • если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;

    • если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;

    • если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.

    написать администратору сайта