Числа и векторы. Тема Действительные числа
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
|
Числа и векторы Тема 1. Действительные числа Развитие понятия числа Наиболее общие закономерности и законы экономических явлений выясняются путем качественного анализа, но конкретное выражение их возможно лишь с помощью меры и числа.  Число — важнейшее математическое понятие, меняющееся на протяжении веков. Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4, ... При счете отдельных предметов единица есть наименьшее число и делить ее на доли не нужно, а иногда и нельзя, однако уже при грубых измерениях величин приходится делить 1 на доли. Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел. Дробью называется часть (доля) единицы или несколько равных ее частей. Обозначаются: Среди десятичных дробей особое место занимают периодические дроби: Дальнейшее расширение понятия числа вызвано уже развитием самой математики (алгебры). Декарт в XVII в. вводит понятие отрицательного числа. Числа целые (положительные и отрицательные), дробные (положительные и отрицательные) и нуль получили название рациональных чисел. Всякое рациональное число может быть записано в виде дроби конечной и периодической. Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа — введение действительных (вещественных) чисел — присоединением к рациональным числам иррациональных: иррациональные числа — это бесконечные десятичные непериодические дроби. Иррациональные числа появились при измерении несоизмеримых отрезков (сторона и диагональ квадрата), в алгебре — при извлечении корней Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — Режим доступа к курсу: http://e-college.ru. — П. 2.1. Числа натуральные (1, 2, 3, ...), целые (..., –3, –2, –1, 0, 1, 2, 3, ...), рациональные (представимые в виде m / n, где m и n ≠ 0 — целые числа) и иррациональные (не представимые в виде m / n) образуют множество действительных (вещественных) чисел. Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 24. Все действительные числа можно изобразить на числовой оси. Числовая ось (числовая прямая): а) горизонтальная прямая с выбранным на ней направлением; б) начало отсчета — точка 0; в) единица масштаба. Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — Режим доступа к курсу: http://e-college.ru. — П. 2.1. Свойства действительных чисел a + b = b + a. а + (b + с) = (а + b) + с. а + 0 = а. а + (–а) = 0. ab = b а. a (bc) = (ab) с. а · 0 = 0. а · 1 = a. a (b + c) = ab + ac . Комплексные числа возникают в связи с задачей решения квадратных и других алгебраических уравнений. Комплексным числомназывается выражение вида z = x + iy , где x и y — действительные числа, i - мнимая единица. Число x называется действительной частью, а y - мнимой частью числа z (обозначаются соответственно x = Re (z), y = Im (z)). Действительное число x является частным случаем комплексного числа z = x + iy при y = 0. Если y ≠ 0, то комплексные числа вида z = x + iy называются мнимыми, а при x = 0, y ≠ 0, т.е. числа вида z = iy , — чисто мнимыми. Числа z = x + iy и z = x – iy называются комплексно-сопряженными. Два комплексных числа z1 = x1 + i y1 и z2 = x2 + i y2 pавны, если x1 = x2, y1 = y2. Число z = 0, если x = 0, y = 0. Отношений «больше», «меньше» для комплексных чисел не существует. Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 25. 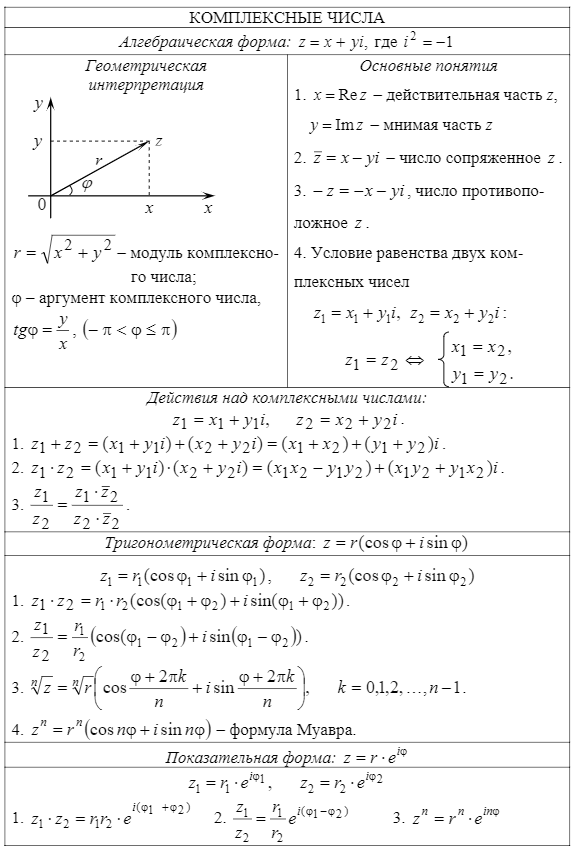 Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 46. Степенью где В частности, 1n = 1; 0n = 0 (n ≠ 0). По определению Правила действий со степенями (а ≥ 0, b > 0, с ≥ 0) (2.2). (abc)n = an bn cn; am × an = am + n; (am)n = amn; Основные алгебраические формулы: а2 – b2 = (а – b) (а + b); (а ± b)3 = а3 ± 3а2b + 3а b2 ± b3; (а ± b)2 = a2 ± 2ab + b2 ; a3 ± b3 = (а ± b) (a2 ± ab + b2); (2.3) (а + b + ... + k + l)2 = а2 + b2 + ... + k2 + l2 + 2 (ab + ... + ak + al + bc +...+ bk + bl + ... + kl); an – bn = (a – b)(an–1 + an–2 b + an–3 b2 + ... + a bn–2+ bn–1). (Например, (a + b + c)2 = a2 + b2 + c2 + 2 (ab + ac + bc); a5 – b5 = (a – b) (a4 + a3b + a2b2 + ab3 + b4). Корнем степени n из числа а называется число, n-я степень которого равна заданному числу где (Например, По определению Действие нахождения корня называется извлечением корня. Арифметическим корнем, или арифметическим значением корня, n-й степени называется неотрицательное число Выражения, содержащие знак корня (радикал), называются иррациональными. Правила действий с корнями (а ≥ 0, b > 0, с ≥ 0; n ≥ 2, p ≥ 2 (n, m ∈ N)): 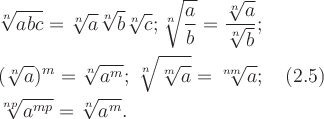 (Например, 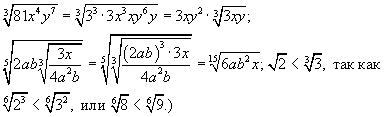 Указанные правила безоговорочно верны для арифметических корней. (Например, а не Для четного n = 2k. т.е. (например, так как так как По определению степень с рациональным (дробным) показателем где (Например, Для степеней с дробным показателем сохраняются те же правила действий со степенями (2.2), приведенные выше. Формула сложного радикала 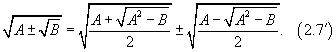 Пример 2.1. Упростить выражения:  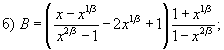 Решение, а) Учитывая формулы (2.2), (2.3), получаем: 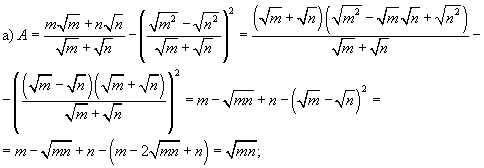 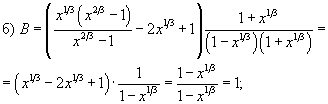  или по формуле (2.7′) 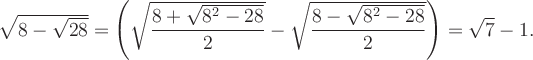 Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 34–37. Запись n ∈ N означает, что n принадлежит множеству натуральных чисел. Z означает множество целых чисел. Тема 2. Скалярные величины и векторы. Действия над векторами. Величины, которые полностью характеризуются своим численным значением, называются скалярными (скалярами): t °, V , m , время, ... Векторы — величины, для характеристики которых необходимо знать не только их числовые значения, но и направление: F , скорость, ускорение. Цит. по: Математика [Электронный ресурс]: учебный курс / Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — Режим доступа к курсу: http://e-college.ru. — П. 3.1. Вектором называется направленный отрезок 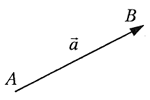 Рис. 4.4 Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например Длиной (модулем, или нормой) Векторы, лежащие на одной прямой или параллельных прямых, называются коллинеарными. Векторы, лежащие в одной плоскости или параллельных плоскостях, называются компланарными. Если начало и конец вектора совпадают, например Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 119. Произведением вектора 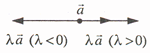 Рис. 4.5 Вектором, противоположным вектору Суммой двух векторов 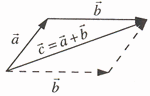 Рис. 4.6 Очевидно, что вектор Аналогично определяется сумма нескольких векторов. Так, например, сумма трех векторов  Рис. 4.7 Если же векторы 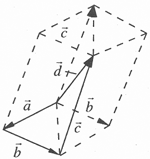 Рис. 4.8 Разностью двух векторов Координатами вектора 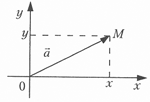 Рис. 4.9 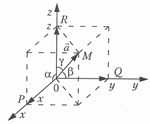 Рис. 4.10 Вектор где Длина вектора (см. рис. 4.9 и 4.10) равна корню квадратному из суммы квадратов его координат: или Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 119–121. Направляющими косинусами вектора при этом Цит. по: Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. — М.: Высшее образование, 2009. — (Основы наук) — С. 121. 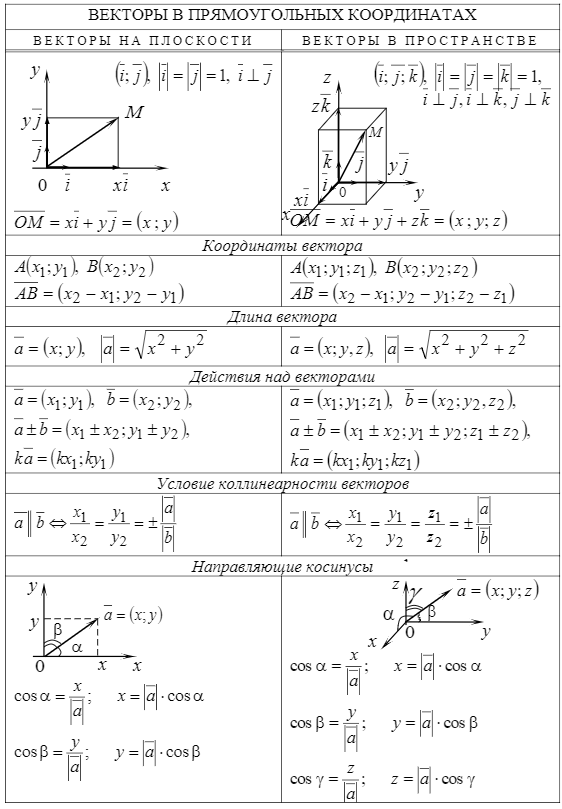 Цит. по: Высшая математика в схемах и таблицах / Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 16. |
