Числа и векторы. Тема Действительные числа
 Скачать 2.01 Mb.
|
|
Тема 2. Прямая и плоскость в пространстве Пример 19* Найти расстояние от точки P (2; 3; –1) до прямой  План решения 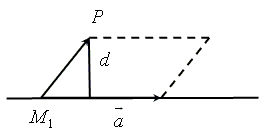 1. Определить координаты направляющего вектора прямой, заданной уравнением  и координаты точки M1 (x0; y0; z0). 2. Найти векторное произведение векторов 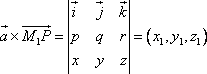 и    3. Найти площадь параллелограмма, построенного на векторах и  4. Найти расстояние d, которое является высотой параллелограмма:  , где  — длина вектора  Решение
Пример 21 Найдите координаты точки K пересечения прямой  с плоскостью x + 2y – 3z – 4 = 0.План решения 1. Уравнение прямой записать в параметрическом виде: 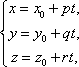 где M0 (x0; y0; z0) — координаты точки,  — координаты направляющего вектора.2. Решить систему уравнений: 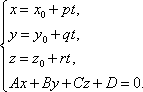 Решение Из канонического уравнения прямой 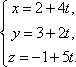возьмем точку M0 (2; 3; –1) и направляющий вектор  и запишем уравнение прямой в параметрическом виде: Решим систему уравнений, состоящую из параметрических уравнений и уравнения плоскости: 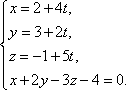 Выражения для x, y и z подставим в последнее уравнение и найдем t : (2 + 4 t) + 2 (3 + 2t) – 3 (–1 + 5 t) – 4 = 0, 2 + 4 t + 6 + 4 t + 3 – 15 t – 4 = 0, –7 t + 7 = 0, t = 1. Делая обратную подстановку, найдем x, y и z:  ,  ,  .Таким образом, координаты точки пересечения прямой и плоскости K (6; 5; 4). Пример 23 Найти острый угол между прямыми  План решения 1. Найти координаты направляющих векторов  2. Воспользоваться формулой 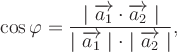 где  — модуль скалярного произведения векторов  и   — длины векторов и Решение Из уравнения прямых имеем 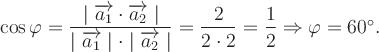   Пример 25 Составить канонические уравнения прямой  План решения 1. Записать канонические уравнения прямой  Чтобы их составить нужно знать координаты точки M0 (x0; y0; z0) и координаты направляющего вектора  2. Найти координаты точки M0. Для этого одну из переменных приравнять к нулю и решить полученную систему. 3. Найти координаты направляющего вектора. В качестве направляющего вектора взять вектор  где  — координаты нормальных векторов плоскостей, определяющих прямую как линию их пересечения, т.е.если  то  Тогда 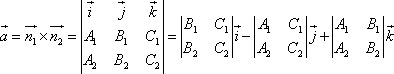 Решение 1. Найдем координаты точки M0. Для этого приравняем в данной системе z к нулю, т.е. пусть z = 0. Тогда система примет вид 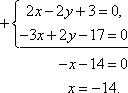  Подставим найденное значение x в первое уравнение системы. 2(–14) – 2y + 3 = 0, –28 – 2y + 3 = 0, – 2y – 25 = 0,  Таким образом, M0 (–14; –12,5; 0) . Замечание Точка M0 может иметь другие координаты. Всё зависит от того, какое значение и какой переменной придается. 2. Найдем координаты направляющего вектора. Для этого определим координаты нормальных векторов:  и  Тогд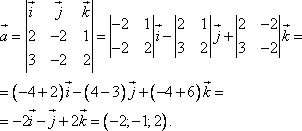а  Таким образом, канонические уравнения имеют вид  Пример 27 Составить канонические уравнения прямой, проходящей через точки с координатами (3; –4; 2) и (2; 5; –1). План решения 1. Воспользоваться уравнением прямой, проходящей через две точки M1 (x1; y1; z1) и M2 (x2; y2; z2):  Решение  и  .  Пример 29 Составить канонические уравнения прямой, проходящей через точку M1 (5; –3; 2) и параллельно вектору  План решения 1. Воспользоваться уравнением  где M0 (x0; y0; z0) — координаты точки; — координаты направляющего вектора.Решение  Пример 31* Составить уравнение плоскости, которая проходит через ось Oy и точку M1 (3; –2; 5). План решения Для составления данного уравнения плоскости следует воспользоваться условием компланарности трех векторов. 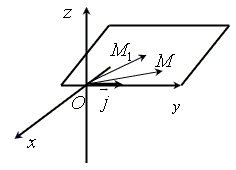 1. Взять точку M (x; y; z) с текущими координатами, лежащую в искомой плоскости. 2. Найти координаты векторов  и  3. На оси Oy взять единичный вектор  4. Составить уравнение плоскости в виде 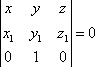 т.е.  .Решение Возьмем точку M (x; y; z). Найдем координаты векторов и    Составим уравнение 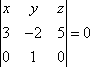 , ,–5x + 3z = 0. Цит. по: Методическое пособие-тренажер решения задач по высшей математике / Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 11–16. Тема 3. Взаимное расположение прямых Пример 33* Вычислить кратчайшее расстояние между прямым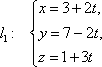и  и 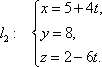 План решения 1. Найти координаты точек, лежащих на прямых. Если прямая задана параметрическими уравнениям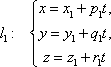и  и 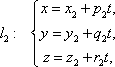 то M 1 (x 1 ; y 1 ; z 1) и M 2 (x 2 ; y 2 ; z 2).2. Найти координаты направляющих векторов  3. Воспользоваться формулой 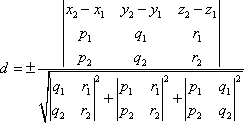 ,знак «+» берется, если определитель третьего порядка положителен, «–» — в противном случае. Решение M1 (3; 7; 1), M 2 (5; 8; 2), 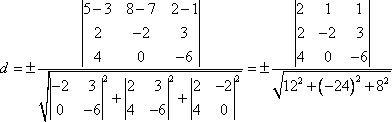  ;вычислим отдельно 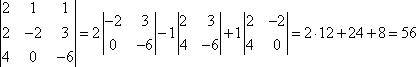 .Таким образом,  Цит. по: Методическое пособие-тренажер решения задач по высшей математике / Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 16–17. |
координаты точки M1 (1; 2; 13), координаты направляющего вектора 
.
.
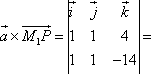
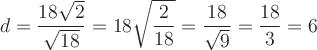— расстояние от точки P до прямой.
и 
- это вектор, координаты которого определяются формулой
, т.е. площадь параллелограмма равна длине вектора векторного произведения.