Математика. Решение. 1 Расстояние между двумя точками и вычисляют по формуле Тогда длина ребра
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
11–20. Даны координаты вершин пирамиды A1,A2,A3,A4. Найти: 1) длину ребра A1A2; 2) угол между ребрами A1A2 и A1A4; 3) площадь грани A1A2A3; 4) объем пирамиды; 5 уравнения прямой A1A2; 6) уравнение плоскости A1A2A3; 4) уравнения высоты, опущенной из вершины A4 на грань A1A2A3. Сделать схематический чертеж. 13. Решение. 1) Расстояние между двумя точками Тогда длина ребра 2) Угол φ между векторами 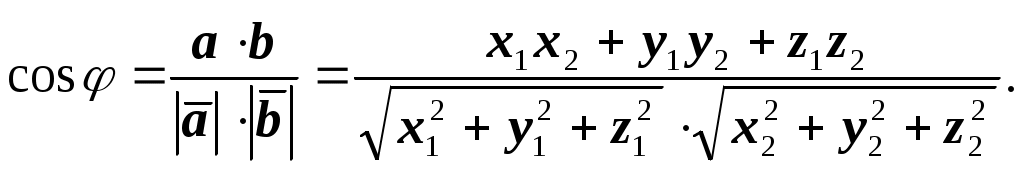 Найдем координаты векторов 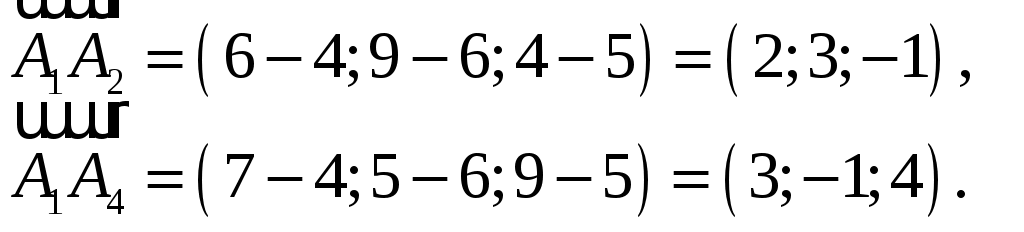 Тогда 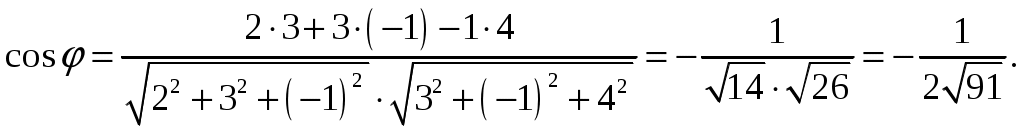 3) Площадь грани находится по формуле 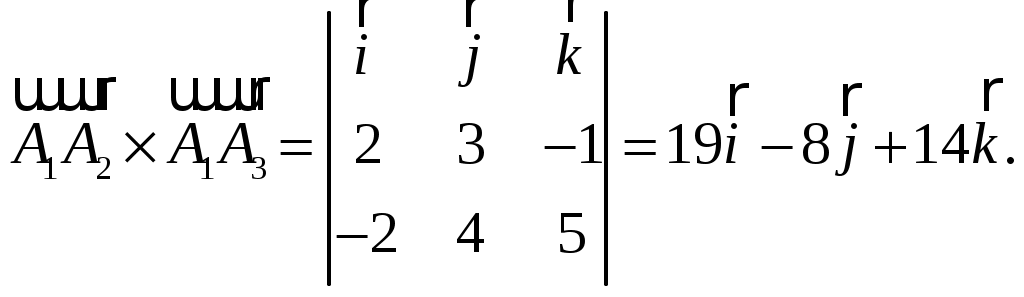 4) Объем пирамиды находят по формуле 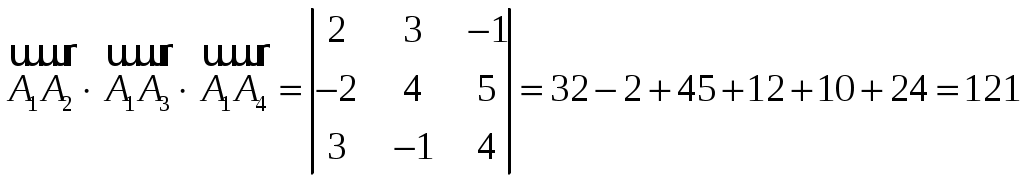 5) Канонические уравнения прямой, проходящей через две точки, имеют вид: Подставив координаты точек 6) Составим уравнение плоскости 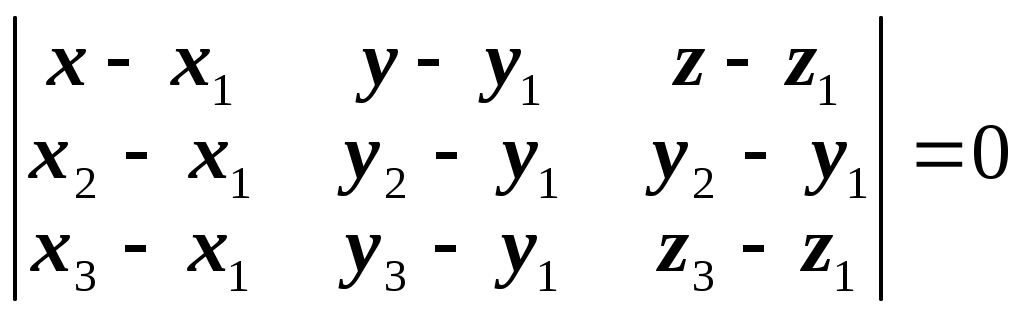 , где , где В нашем случае для плоскости 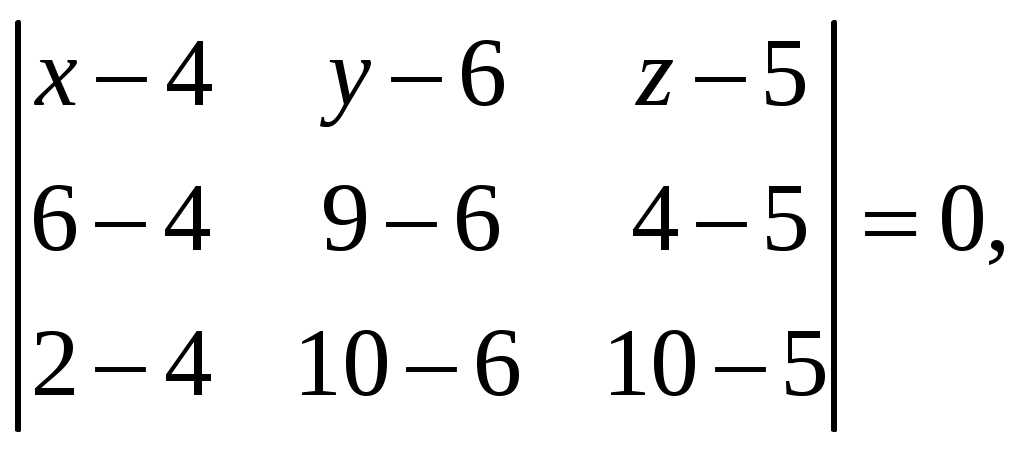 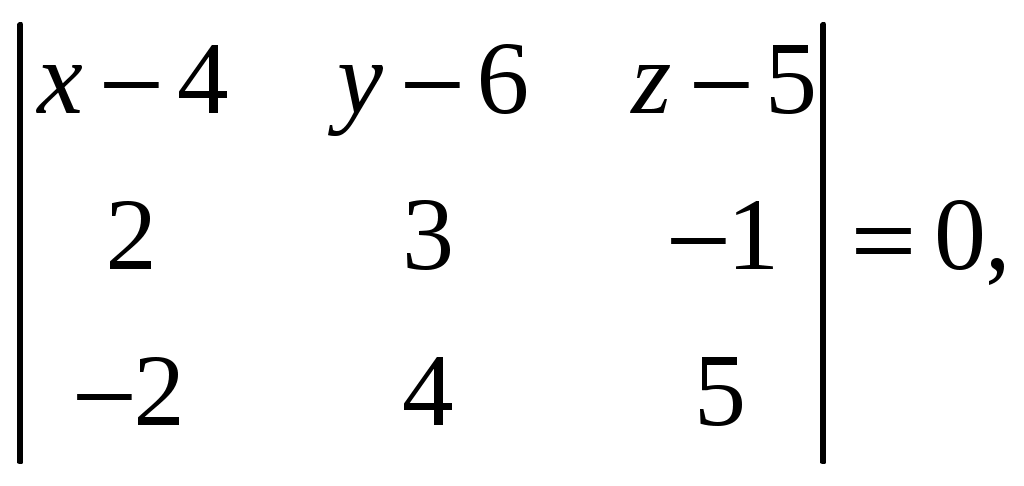 7) Канонические уравнения прямой, проходящей через точку Направляющим вектором высоты, опущенной из вершины Тогда Делаем чертёж.  21-30. Найдите точку 23. Решение. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку Каноническое уравнение прямой: Так прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е. Поэтому уравнение прямой будет Найдем точку пересечения прямой и плоскости. Пусть: 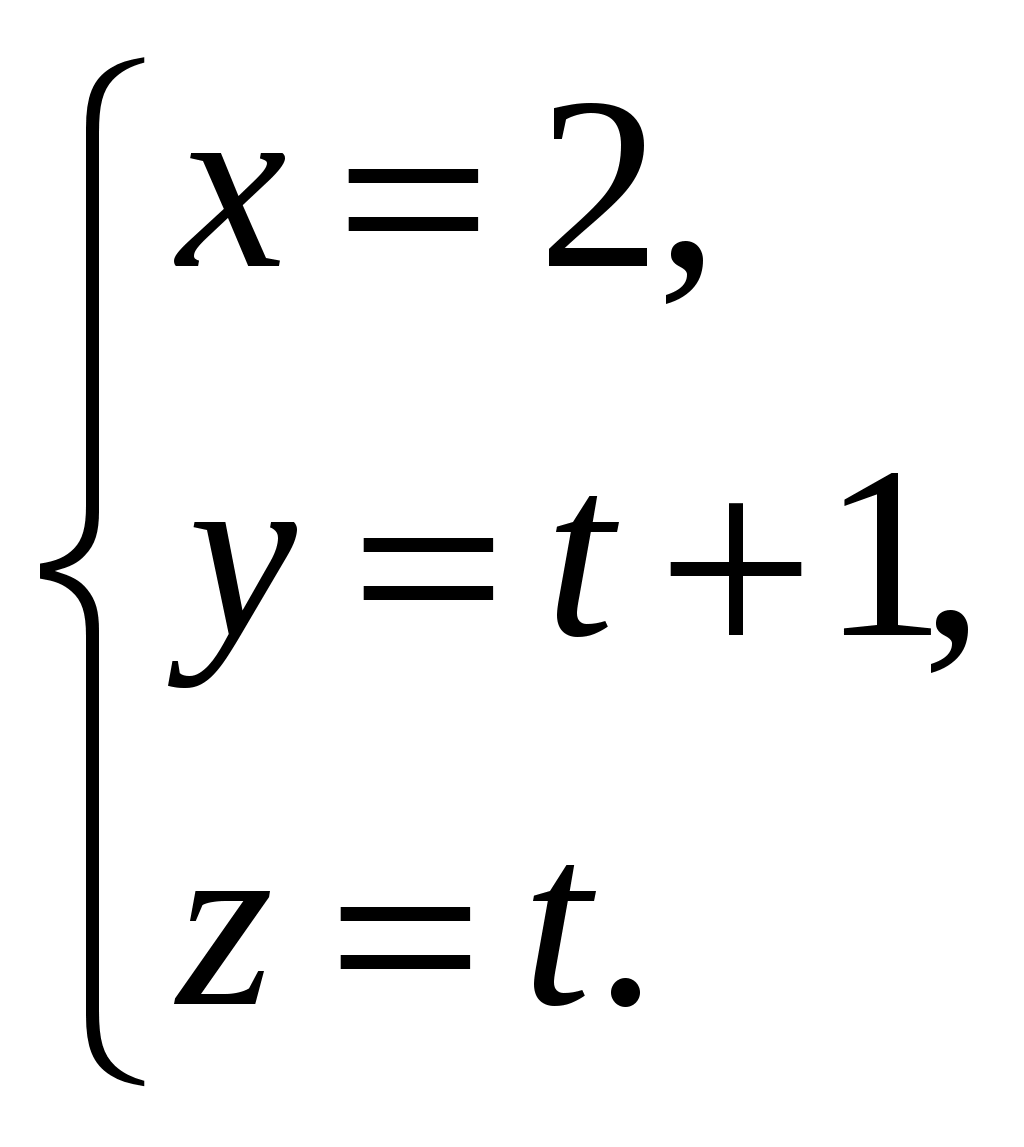 Подставляем в уравнение плоскости: Откуда Т.е. Ответ: 31—40. Дана система линейных уравнений. Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления. 33. 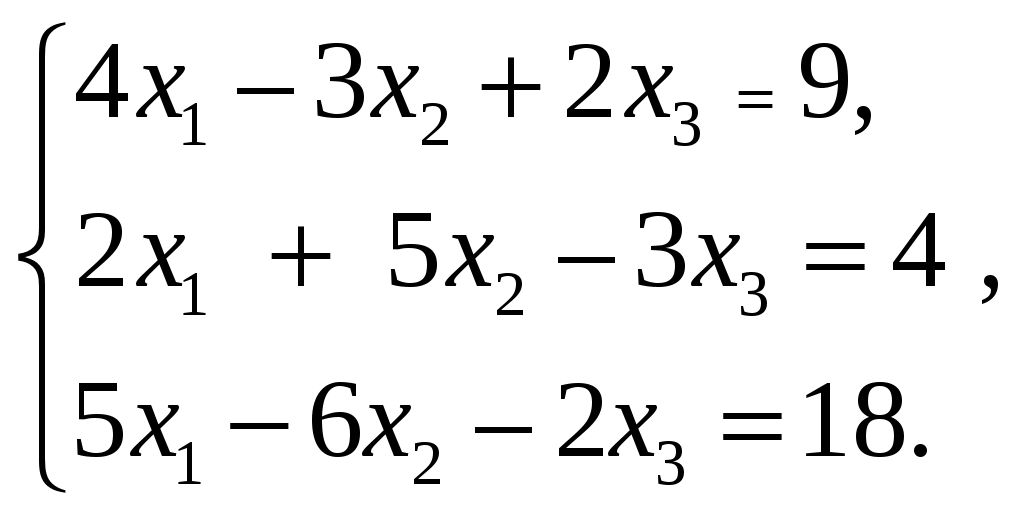 Решение. Совместность данной системы докажем, используя теорему Крамера, а именно: если главный определитель отличен от нуля, то система имеет единственное решение. Находим главный определитель системы: 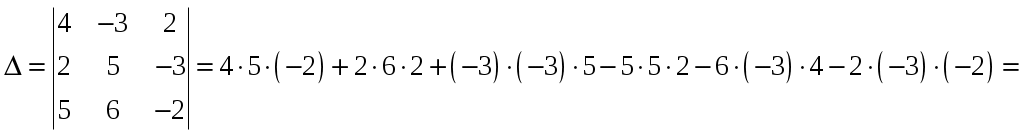 Решим заданную систему: 1) методом Гаусса. C помощью элементарных преобразований строк расширенную матрицу системы 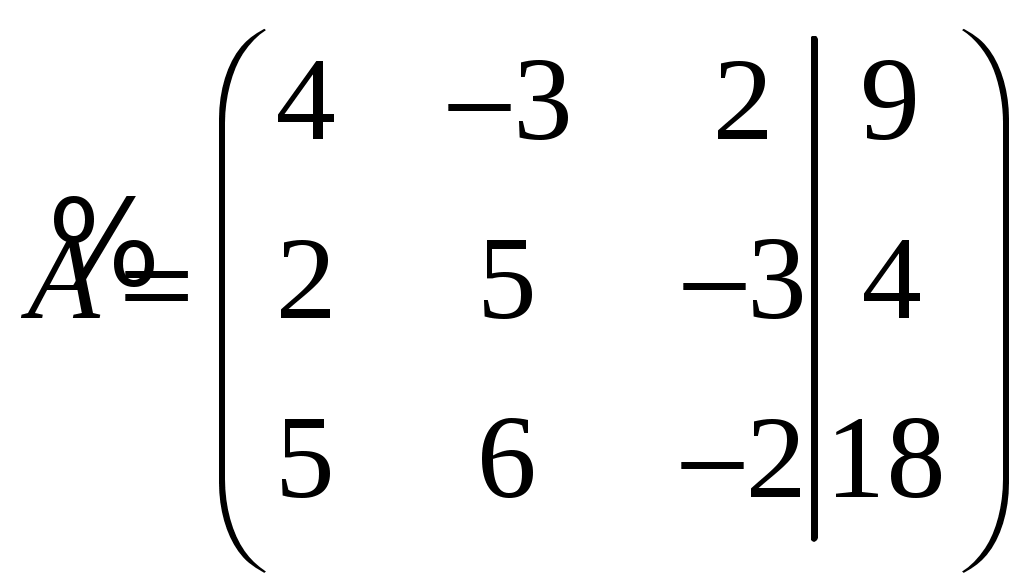 приведем к следующему виду: приведем к следующему виду: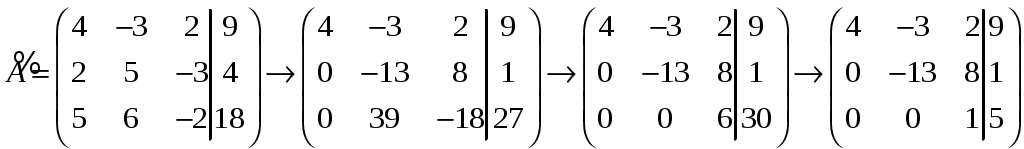 Изменяем вторую, третью строки: ко второй строке, умноженной на (-2) по элементам прибавляем первую строку, к третьей, умноженной на 4– первую строку, умноженную на (-5). Изменяем третью строку: к третьей строкепо элементам прибавляем вторую строку, умноженную на 3. Делим последнюю строку на 6. Т.к. 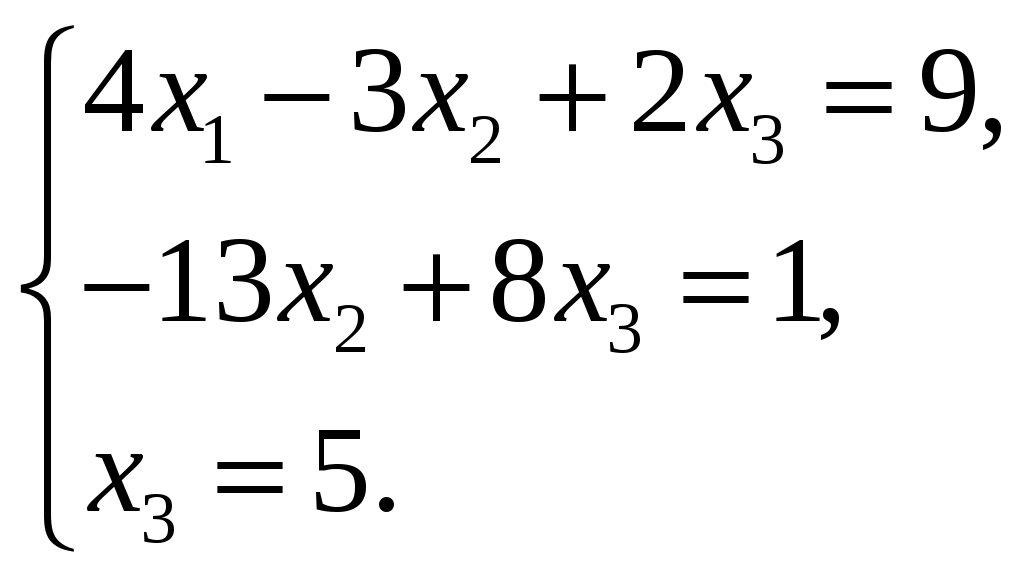 Которая эквивалентна исходной. Из данной системы следует, что 2) Средствами матричного исчисления: Для нахождения решения СЛАУ с помощью обратной матрицы запишем систему уравнений в матричной форме AX=B, где 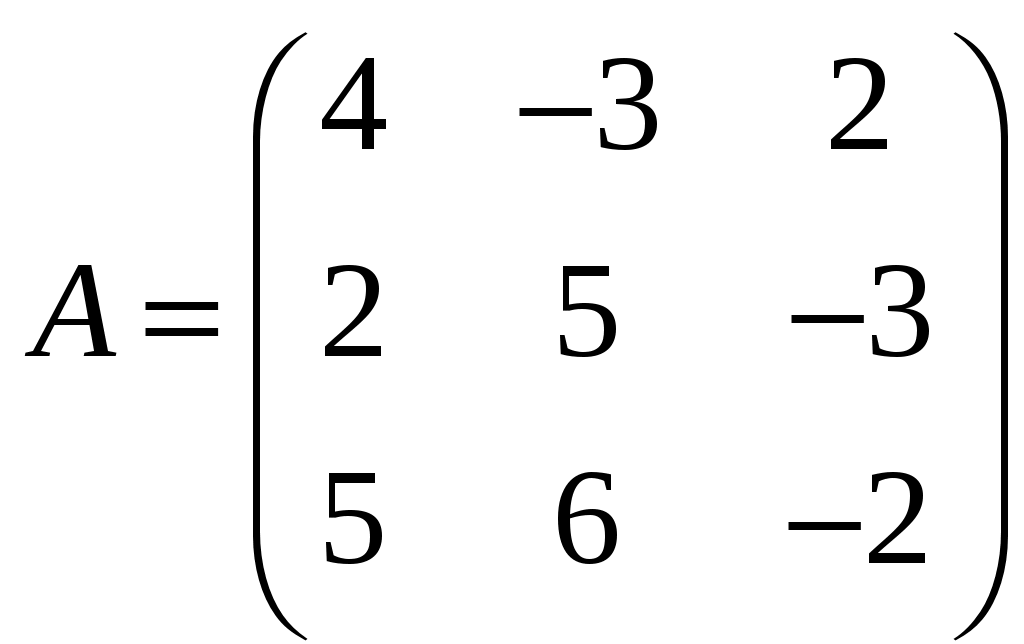 , , 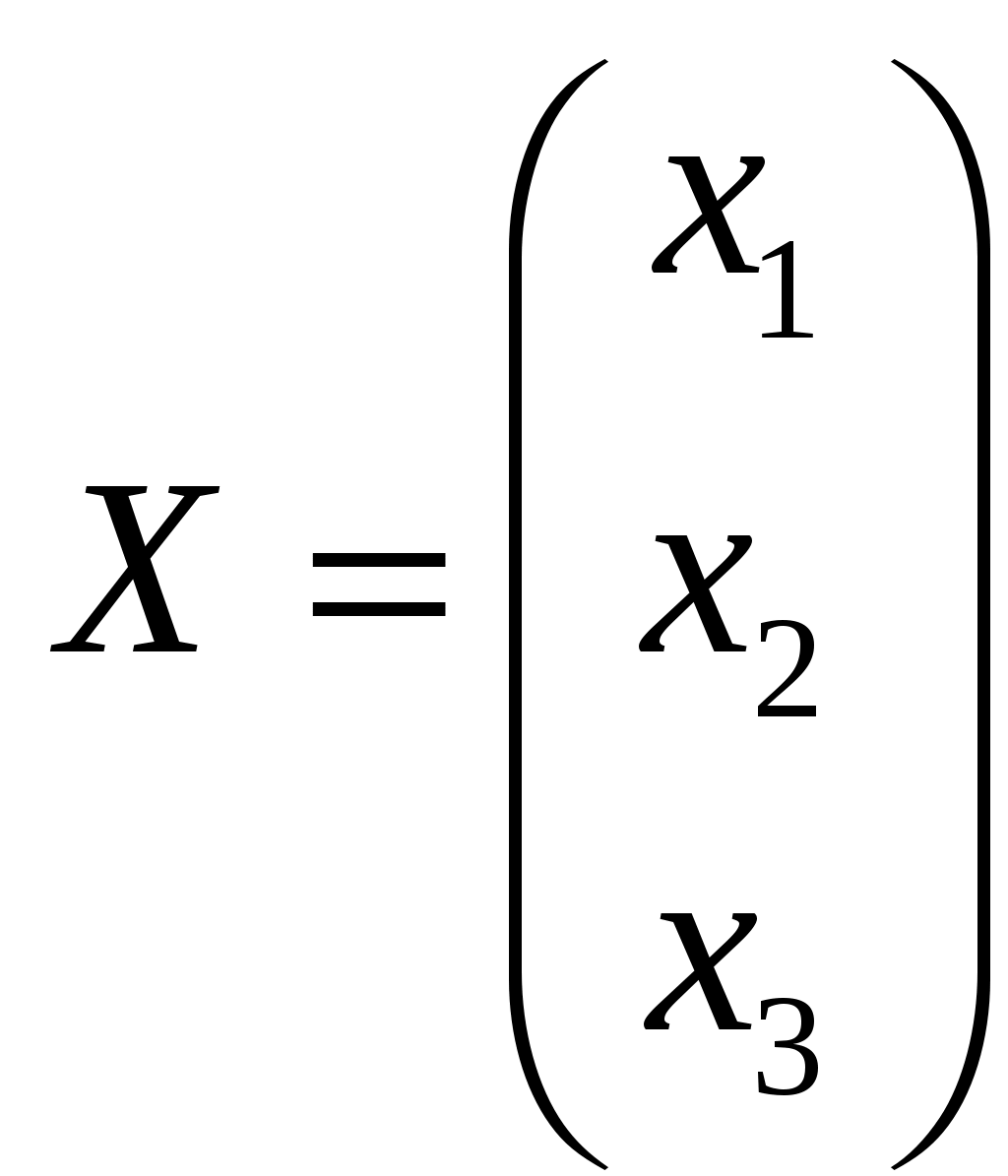 , , 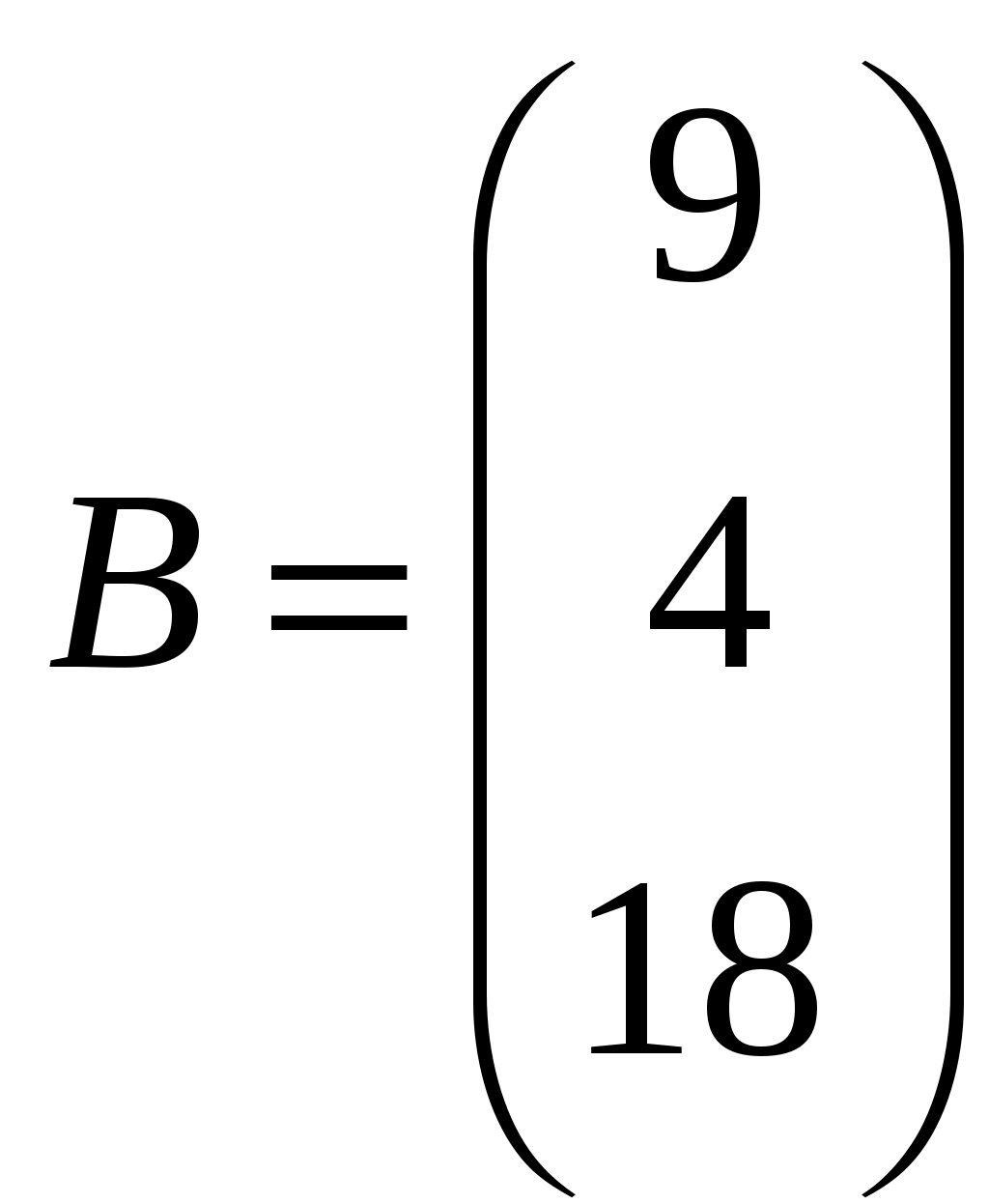 . .Решение СЛАУ в матричной форме имеет вид 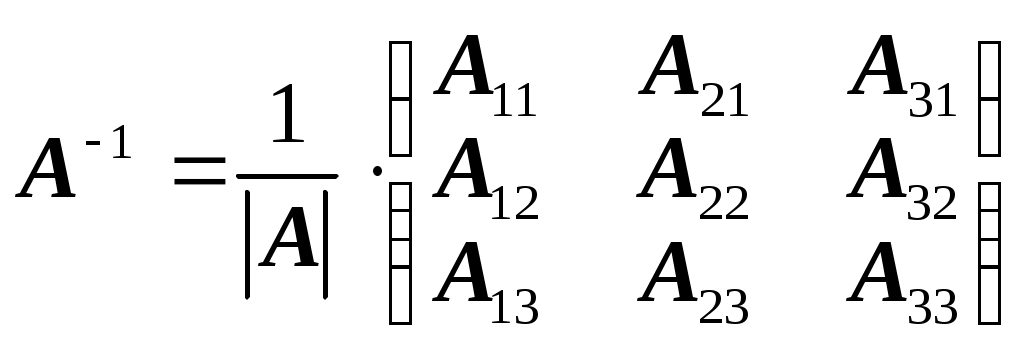 , где , где 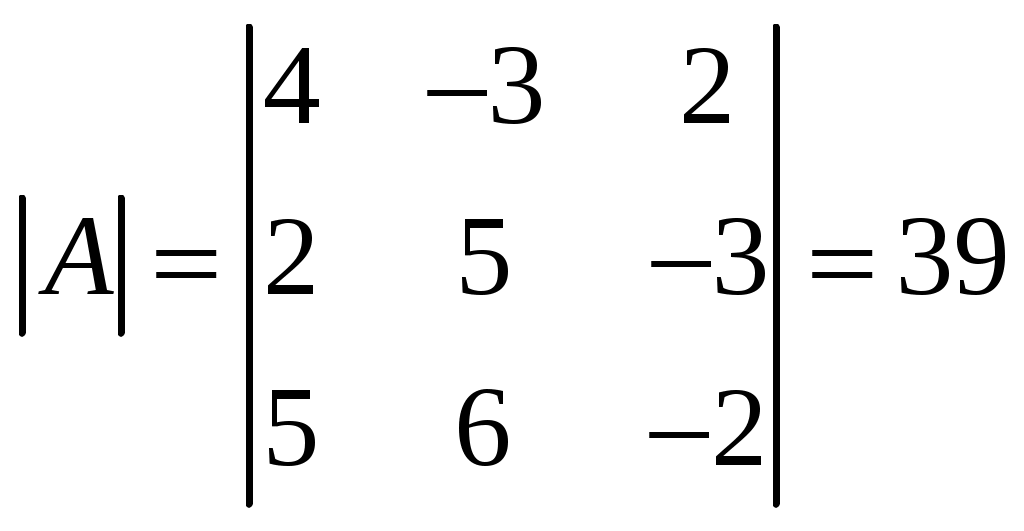 , ,
Обратная матрица имеет вид: 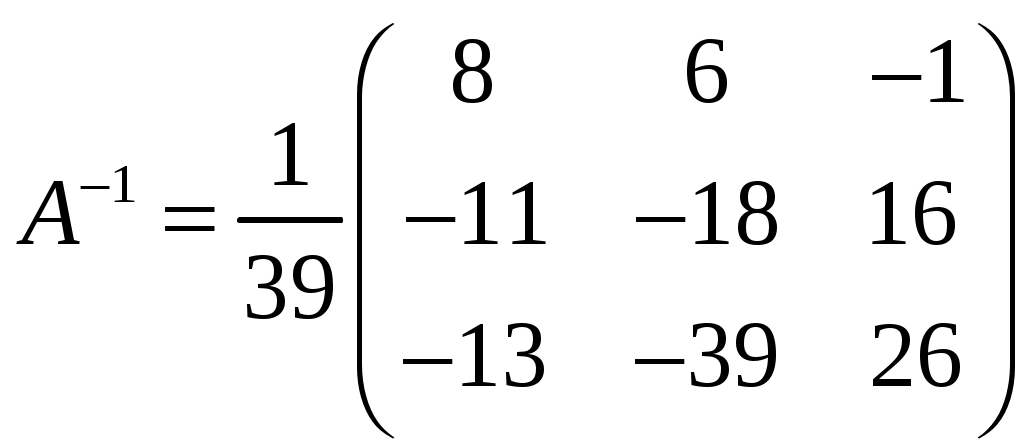 . .Итак: 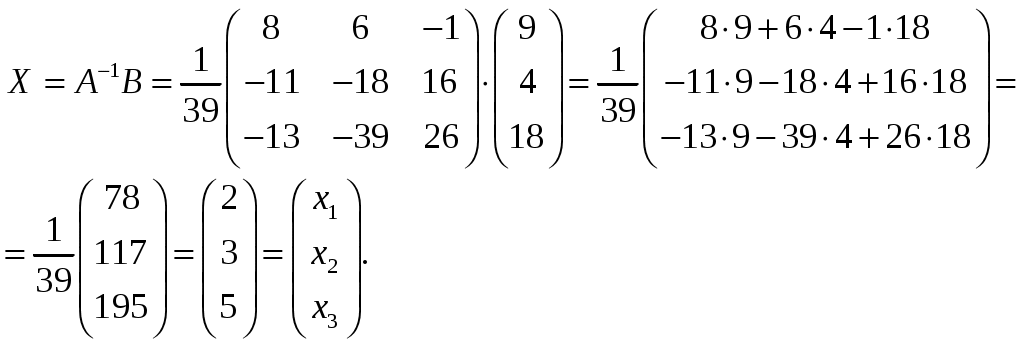 Итак, решение системы: Ответ: 41-50.Найти пределы функций, не пользуясь правилом Лопиталя. 43. а) б) в) Решение. а) В этом случае имеем неопределенность вида 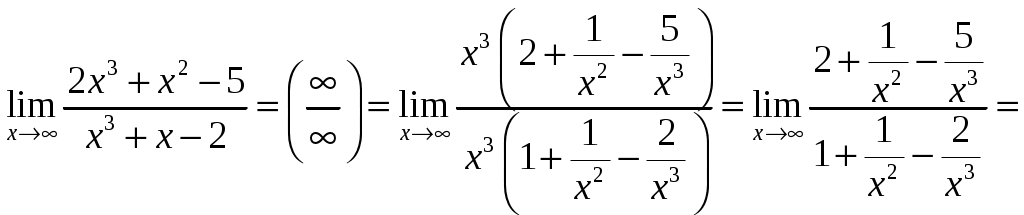 б) Под знаком предела есть иррациональность в числителе дроби. Непосредственная подстановка предельного значения аргумента x= 1 приводит к неопределенности вида Чтобы раскрыть эту неопределенность, достаточно числитель и знаменатель дроби, стоящей под знаком предела, домножить на выражение, сопряженное числителю дроби: 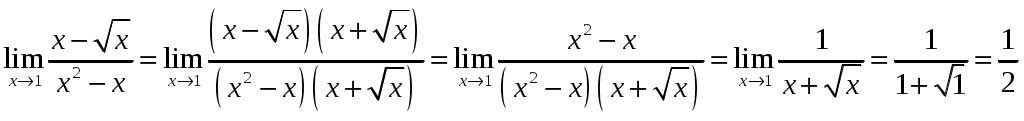 . .в) Непосредственная подстановка предельного значения аргумента x= 0 приводит к неопределенности вида Чтобы раскрыть эту неопределенность, преобразуем выражение: 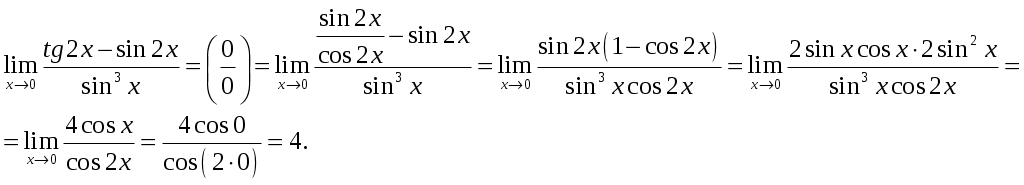 г) При 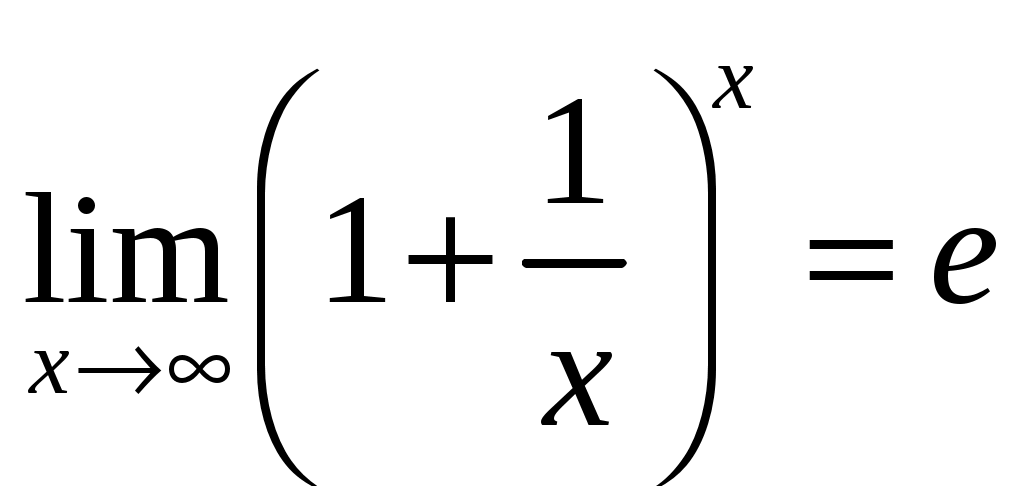 : :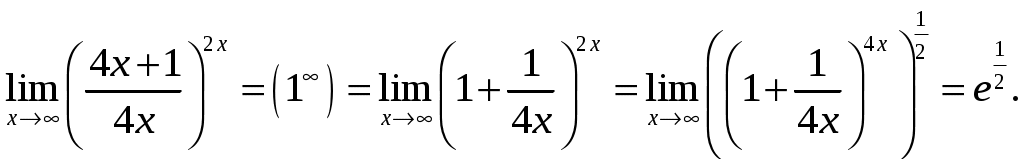 д) При 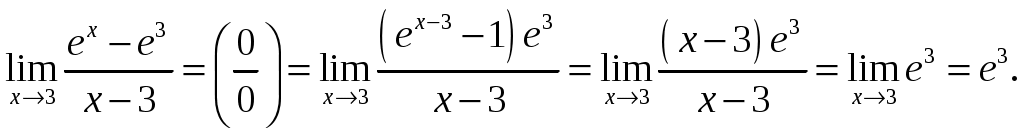 51-60. Задана функция у=f(х)и два значения аргумента x1и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва определить какого он рода; 3) все рассуждения обосновать. 53. Решение. Чтобы проверить непрерывность заданной функции Найдем область определения функции (ООФ): Точка 1) Чтобы определить тип разрыва, вычислим односторонние пределы функции при Так как один из односторонних пределов оказался бесконечным, делаем вывод, что в точке Точка 1) 2) существует конечный предел 3) справедливо 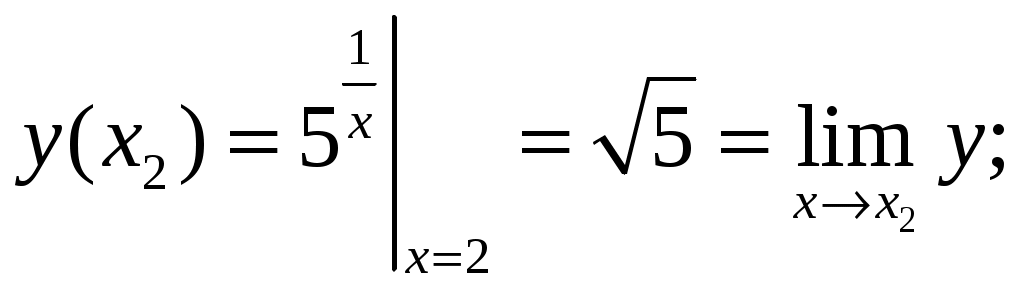 следовательно, в точке Построим схематический чертеж графика функции в окрестности точки разрыва с учетом значений односторонних пределов. 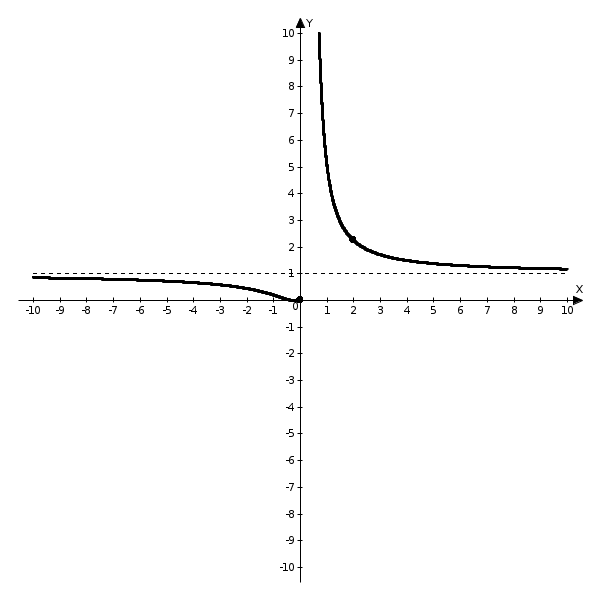 61-70. Найти производные 63. а) Решение. а) Используя правило дифференцирования сложной функции и табличные формулы, получим: б) Используя правило дифференцирования сложной функции и табличные формулы, получим: 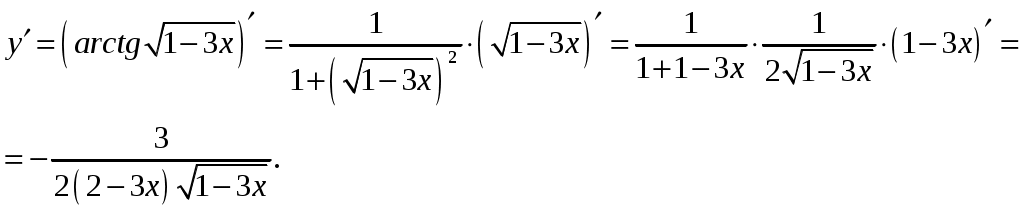 в) Прологарифмируем обе части исходного равенства: Применим свойство логарифмов: Дифференцируем обе части равенства по 71-80. Найти 73. Решение. Дифференцирование данных функций производится по правилу: 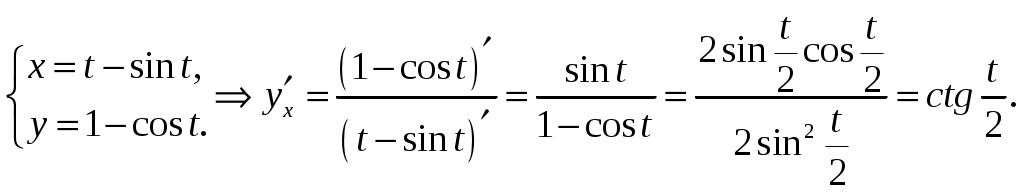 , ,При параметрическом задании функции вторую производную находим по формуле: 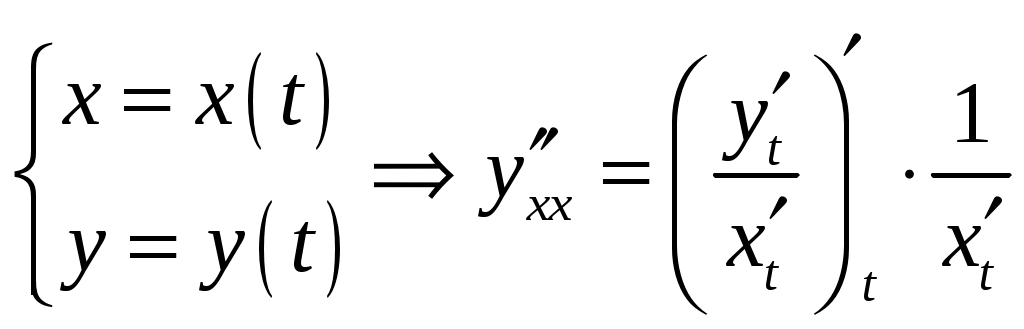 . . 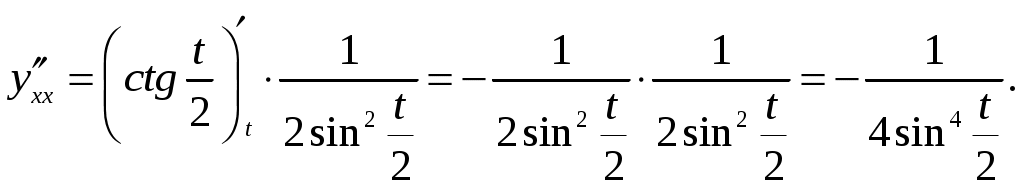 81-90. Найти уравнения касательной к графику функции 83. Решение. Уравнение касательной: Находим производную функции и вычисляем ее значение при Тогда уравнение касательной: Ответ: 91-100. Вычислить предел, применяя правило Лопиталя: 93. Решение. При Применим правило Лопиталя: 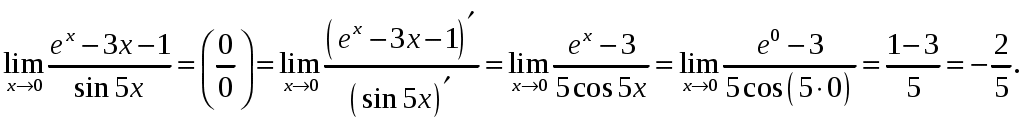 Ответ: |
