ИП. Теоретические основы импульса Понятие и импульса Исторические сведения

Название	Теоретические основы импульса Понятие и импульса Исторические сведения
Дата	11.09.2018
Размер	40.89 Kb.
Формат файла
Имя файла	ИП.docx
Тип	Глава #50392

Введение
Содержание

Глава 1. Теоретические основы импульса

Понятие и импульса
Исторические сведения
Определение импульса в классической и релятивисткой механике
Обобщённый импульс в теоретической механике
Импульс в квантовой механике
Импульс в нерелятивистской квантовой механике

Понятие
И́мпульс (коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы (m)
{\displaystyle m}{\displaystyle m} этого тела на его скорость (v) {\displaystyle v}, направление импульса совпадает с направлением вектора скорости:
p=mv
В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:
Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.
Импульсом тела p (количеством движения) называется векторная физическая величина, численно равная произведению массы тела на его скорость.

Импульс покоящегося тела равен нулю.
Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

{\displaystyle {\vec {p}}=m{\vec {v}}.}
Таким образом, импульс тела — это характеристика движения тела, которая напрямую зависит от его массы и скорости. Чем больше масса и/или скорость движения тела, тем больше его импульс, а значит, тем большее воздействие тело способно оказать на другие тела при взаимодействии с ними. Импульс покоящегося тела равен нулю.
Исторические сведения

История появления термина

Средневековые натурфилософы, в соответствии с учением Аристотеля, полагали, что для поддержания движения непременно требуется некоторая сила, без силы движение прекращается. Часть учёных выдвинула возражение против этого утверждения: почему брошенный камень продолжает двигаться, хотя связь с силой руки утрачена?

Для ответа на подобные вопросы Жан Буридан (XIV век) изменил ранее известное в философии понятие «импетус». По Буридану, летящий камень обладает «импетусом», который сохранялся бы в отсутствие сопротивления воздуха. При этом «импетус» прямо пропорционален скорости. В другом месте он пишет о том, что тела с бо́льшим весом способны вместить больше импетуса.

В первой половине XVII века Рене Декартом было введено понятие «количества движения». Он высказал предположение о том, что сохраняется не только количество движения одного тела, изолированного от внешних воздействий, но и любой системы тел, взаимодействующих лишь друг с другом. Физическое понятие массы в то время ещё не было формализовано — и он определил количество движения как произведение «величины тела на скорость его движения». Под скоростью Декарт подразумевал абсолютную величину (модуль) скорости, не учитывая её направление. Поэтому теория Декарта согласовывалась с опытом лишь в некоторых случаях (например, Валлис, Рен и Гюйгенс в 1668 году использовали её для исследования абсолютно упругого столкновения в системе центра масс).

Валлис в 1668 году первым предложил считать количество движения не скалярной, а направленной величиной, учитывая направления с помощью знаков «плюс» и минус». В 1670 году он окончательно сформулировал закон сохранения количества движения. Экспериментальным доказательством закона послужило то, что новый закон позволял рассчитывать неупругие удары, а также удары в любых системах отсчёта.

Закон сохранения количества движения был теоретически доказан Исааком Ньютоном через третий и второй закон Ньютона. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

Примечательно то, что ранее, в советское время, импульс тела называли количеством движения.

Определение импульса в классической и релятивисткой механике

Классическая механика

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

$\vec p=\sum_{i}m_i \vec{v}_i,$

соответственно величина $\vec p_i=m_i \vec{v}_i$ {\displaystyle {\vec {p}}_{i}=m_{i}{\vec {v}}_{i}}называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).

Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками, и просуммировать по ним, в результате получим:

$\vec p=\int \rho(x,y,z)\vec{v}(x,y,z)dx dy dz$

{\displaystyle {\vec {p}}=\int \rho (x,y,z){\vec {v}}(x,y,z)dxdydz.}

Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:

{\displaystyle {\frac {d{\vec {p}}}{dt}}=0.} $\frac{d\vec p}{dt}=0$ . (*)

Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).

Релятивистская механика

В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина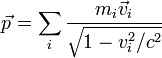

$\vec p = \sum_i \frac{m_i \vec v_i}{\sqrt{1-v_i^2/c^2}}$ ,

где m_i — масса покоя i-й материальной точки.

Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как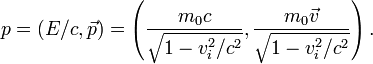

$p=(e/c,\vec p)=\left(\frac{m_0 c}{\sqrt{1-v_i^2/c^2}},\frac{m_0 \vec v}{\sqrt{1-v_i^2/c^2}}\right).$

В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однакодля взаимодействующих частиц в релятивистской механике следует учитывать импульсы не толькосоставляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо болееосмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.

Обобщённый импульс в теоретической механике

В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости

$p_i = \partial {\mathcal l}/\partial \dot{q}_i$

В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа

$dp_i/dt=0\,\!$

Для свободной частицы в релятивистской механике функция Лагранжа имеет вид: 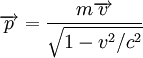$\mathcal l=-mc^2 \sqrt{1-v^2/c^2}$ , отсюда:

$\overrightarrow {p}= \frac{m \overrightarrow {v}}{ \sqrt{1-v^2/c^2}}$

Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).

Импульс в квантовой механике

В квантовой механике, импульс определяется как оператор над волновой функцией, которая коммутирует с гамильтонианом системы и сохранение которого следует из однородности пространства. Принцип неопределенности Гайзенберга определяет границу погрешности, с которой координата частицы может быть измерена одновременно с соответствующей компонентой импульса вдоль той же оси. В квантовой механике погрешности измерения координаты частицы

ΔxΔx

и соответствующей компоненты импульса

ΔpxΔpx

не могут одновременно равняться нулю:

ΔpxΔx≥ℏΔpxΔx≥ℏ

.

Для отдельной частицы с нулевым электрическим зарядом и спином, оператор импульса

pˆp^

определяется как

pˆ=−iℏ∇p^=−iℏ

где

=(∂∂x,∂∂y,∂∂z)

=(∂∂x,∂∂y,∂∂z)

— оператор градиента.

Поскольку результат дифференцирования по двум независимым переменным не зависит от порядка дифференцирования, то операторы трех компонентов импульса коммутативные:

pˆxpˆy−pˆypˆx=0,pˆxpˆz−pˆzpˆx=0,pˆypˆz−pˆzpˆy=0.p^xp^y−p^yp^x=0,p^xp^z−p^zp^x=0,p^yp^z−p^zp^y=0.

Из этого следует, что все три компонента импульса могут одновременно иметь определенные точные значения.

Собственные функции и собственные значения оператора импульса являются решениями уравнения:

−iℏ∇ψ=pψ−iℏ∇ψ=pψ

и имеют следующий вид:

ψ=const⋅eipr/ℏψ=const⋅eipr/ℏ

.
Импульс в нерелятивистской квантовой механике

Формальное определение

В квантовой механике импульсом частицы называют оператор — генератор группы трансляций. Это эрмитовоператор, собственные значения которого отождествляются с импульсом системы частиц. В координатномпредставлении для системы нерелятивистских частиц он имеет вид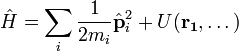

$\hat\mathbf{p} = \sum_j \hat\mathbf{p}_j= \sum -i\hbar \nabla_j$

где $\nabla_j$ — оператор набла, соответствующий дифференцированию по координатам j-ой частицы. Гамильтониан системы выражается через оператор импульса:

$\hat{h} = \sum_i \frac{1}{2m_i}\hat\mathbf{p}_i^2 + u(\mathbf{r_1},\dots)$

Для замкнутой системы (U = 0) оператор импульса коммутирует с гамильтонианом и импульс сохраняется.

Определение через волны де Бройля

Формула де Бройля связывает импульс и длину волны де Бройля.

Модуль импульса обратно пропорционален длине волны {\displaystyle \lambda }λ:

где {\displaystyle h}h — постоянная Планка.

Для частиц не очень высокой энергии, движущихся со скоростью v << c (cкорости света), модуль импульса равен p = mv (где m – масса частицы), и

.

Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.

В векторном виде это записывается как:

Где

- волновой вектор.
Список источников
https://ru.wikipedia.org/wiki/%D0%98%D0%BC%D0%BF%D1%83%D0%BB%D1%8C%D1%81
http://www.yaklass.ru/p/fizika/9-klass/zakony-sokhraneniia-v-mekhanike-90005/impuls-tela-90006/re-09011a73-bfcd-472e-bf28-8c2ddfbfece3
http://class-fizika.narod.ru/9_18.htm
https://lampa.io/p/импульс-тела.-импульс-силы.-закон-сохранения-импульса-00000000453739789fd2a88522635bb3
https://dic.academic.ru/dic.nsf/ruwiki/939304

http://cyclowiki.org/wiki/%D0%98%D0%BC%D0%BF%D1%83%D0%BB%D1%8C%D1%81