|
|
План - конспект открытого занятия по теме Тригонометрические тождества. Конспект занятия по теме _Тригонометрические тождества_ (1 курс). Тригонометрические тождества
План-конспект занятия
по ОДБ.04 Математика
на тему «Тригонометрические тождества»
группа 15ЖКХ
Разработала:
преподаватель Наумёнок Р.А.
2022 год
Тема урока. «Тригонометрические тождества»
Дата проведения.23.11.2022
Тип урока: комбинированный
Технология урока: информационно-коммуникационная
Цели урока:
Образовательная: формирование понятия тождества, умения доказывать тождества и упрощать тригонометрические выражения с использованием изученных формул.
Развивающая: развитие логического мышления, памяти, умений сравнивать, выявлять закономерности, преодолевать трудности при решении математических задач, развитие познавательного интереса учащихся.
Воспитательная: воспитание ответственного отношения к учебному труду, настойчивости для достижения конечных результатов при решении задач.
Задачи урока:
-повторить определение синуса, косинуса, тангенса, котангенса числа ;
-изучить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
-научить применять полученные знания при упрощении тригонометрических выражений, доказательстве тождеств.
Оборудование: мультимедиа-проектор; экран; учебники В.Н.Богомолов «Алгебра и начала анализа», 10-11 класс; раздаточный материал.
Структура и ход урока
Деятельность преподавателя
|
Деятельность обучающихся
|
I. Мотивационно-ориентировочная часть
|
Актуализация.
Слово преподавателя:
- Мы продолжаем изучать главу «Тригонометрические формулы». На прошлых уроках мы познакомились с понятиями синуса, косинуса, тангенса, котангенса и формулами зависимости между ними.
Преподаватель предлагает двум учащимся на доске выполнить № 590 (2) и № 590 (8) из домашнего задания. Во время работы учащихся на доске преподаватель проводит фронтальную работу с группой по повторению пройденного материала.
Слово преподавателя:
- Повторим основные понятия тригонометрии с помощью «Математического лото». Перед вами таблица, содержащая ответы на вопросы, которые будут вам заданы. Ваша задача - найти правильный ответ и назвать квадрат, в котором он находится.

Слайд 1: «Математическое лото».
Переведите в градусную меру угол:
а) π; б)  ; в) ; в) 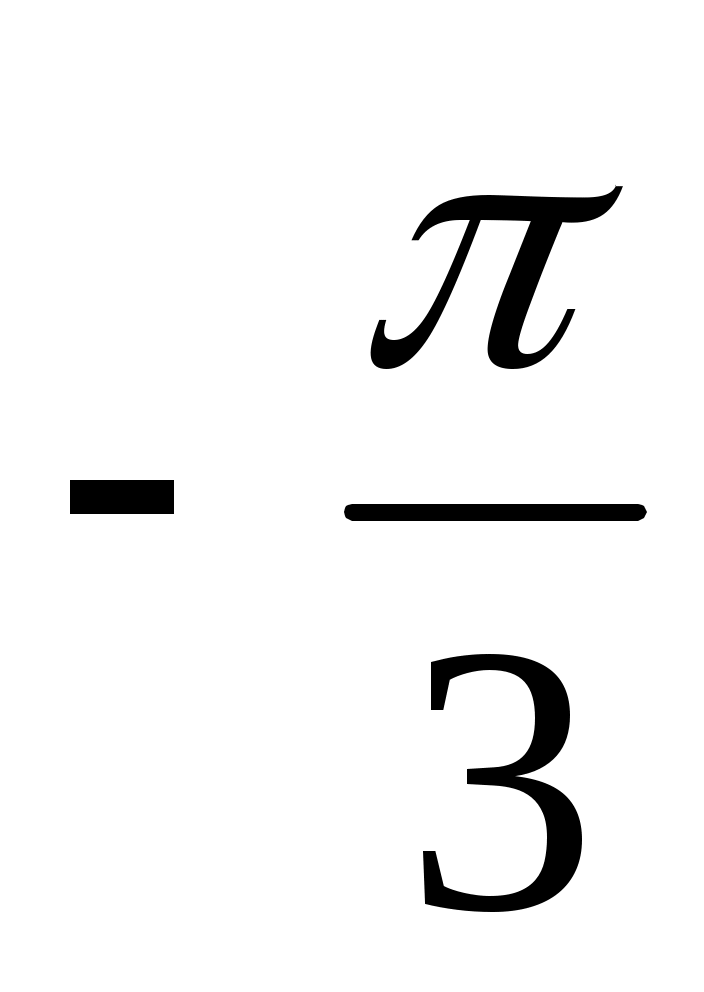 ; г) ; г)  ; д) ; д) 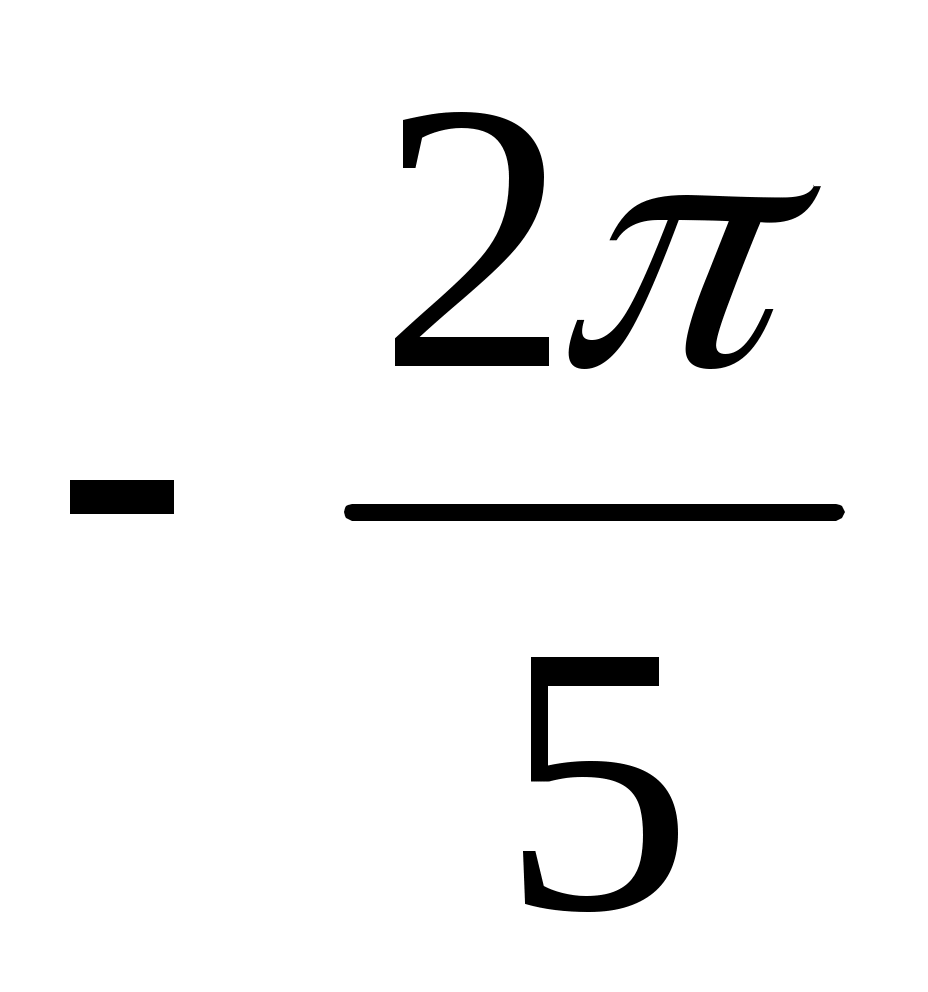
2. Переведите в радианную меру угол:
а) 90º
б) – 180º
в) 360º
г) – 270º
д) 720º
3. Дайте определение sin α, cos α, tg α, ctg α.
4. Вычислите:
а) 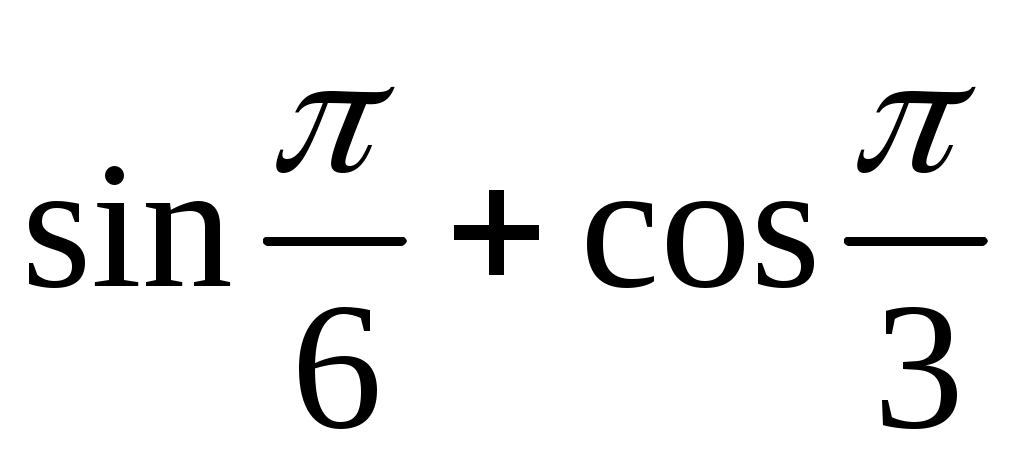
б) 
в) 4сos 90º – 8sin 30º
г) ctg260º + 2
5. Какое из чисел больше 0?
а) sin 340º
б) cos (–120º)
в) sin 50º
г) tg 170º
6. Какие из выражений не имеют смысла?
а) sin 90º
б) cos 0º
в) tg 90º
г) ctg 0º
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
1
|
3π
|
|
|
sin50º
|
- 720º
|
4π
|
|
|
2
|
|
|
абсцисса
|
|
|
|
1
|
|
3
|
|
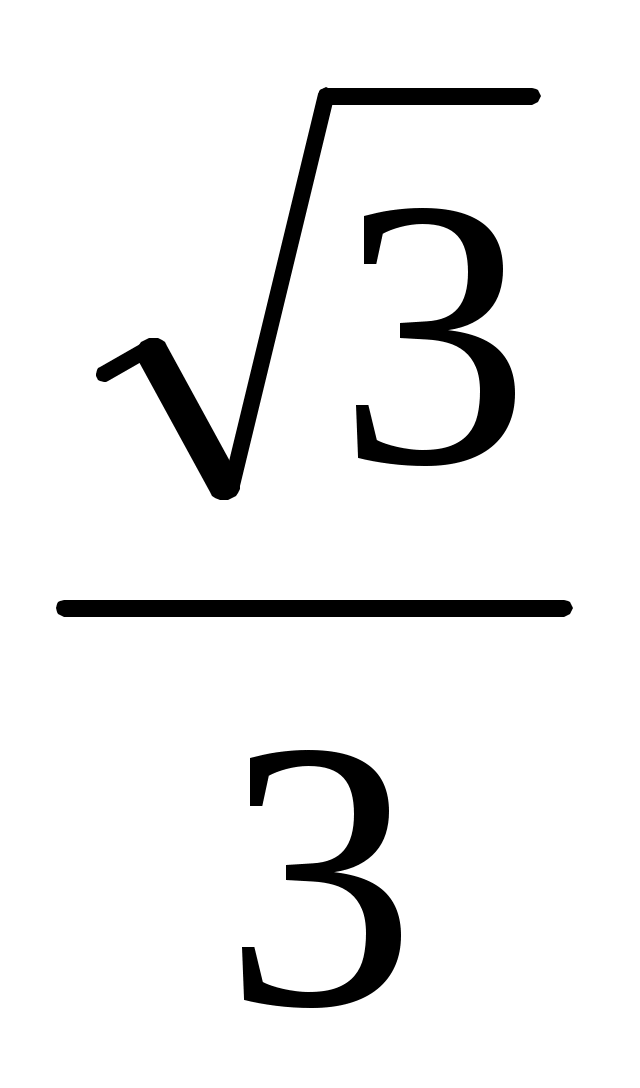
|
|
|
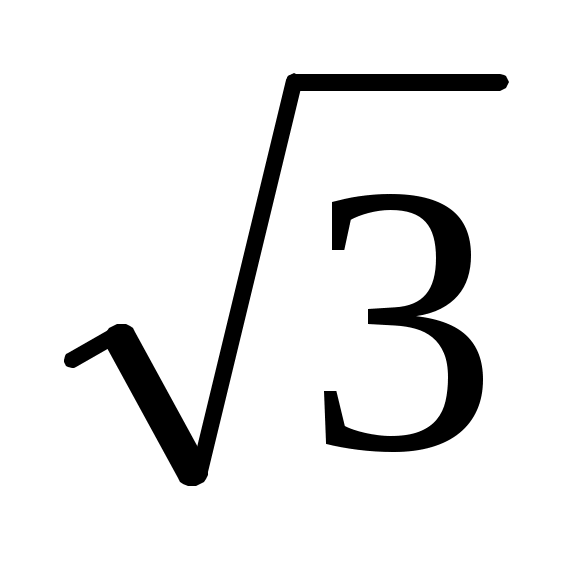
|
|
|
45º
|
4
|
|
|
– 4
|
180º
|

|
|
–π
|
ctg0
|
5
|
|
|
|
|
2π
|
|
|
|
6
|
|
|
cos 0º
|
|
tg90º
|
|
sin90º
|
|
7
|
–36º
|
|
|
|
30º
|
|
|
|
8
|
|
cos(-120º)
|
|
|

|
|
90º
|
|
9
|
|
|
–60º
|
|
ордината
|
|
|
tg170º
|
10
|

|
|
|
|
|
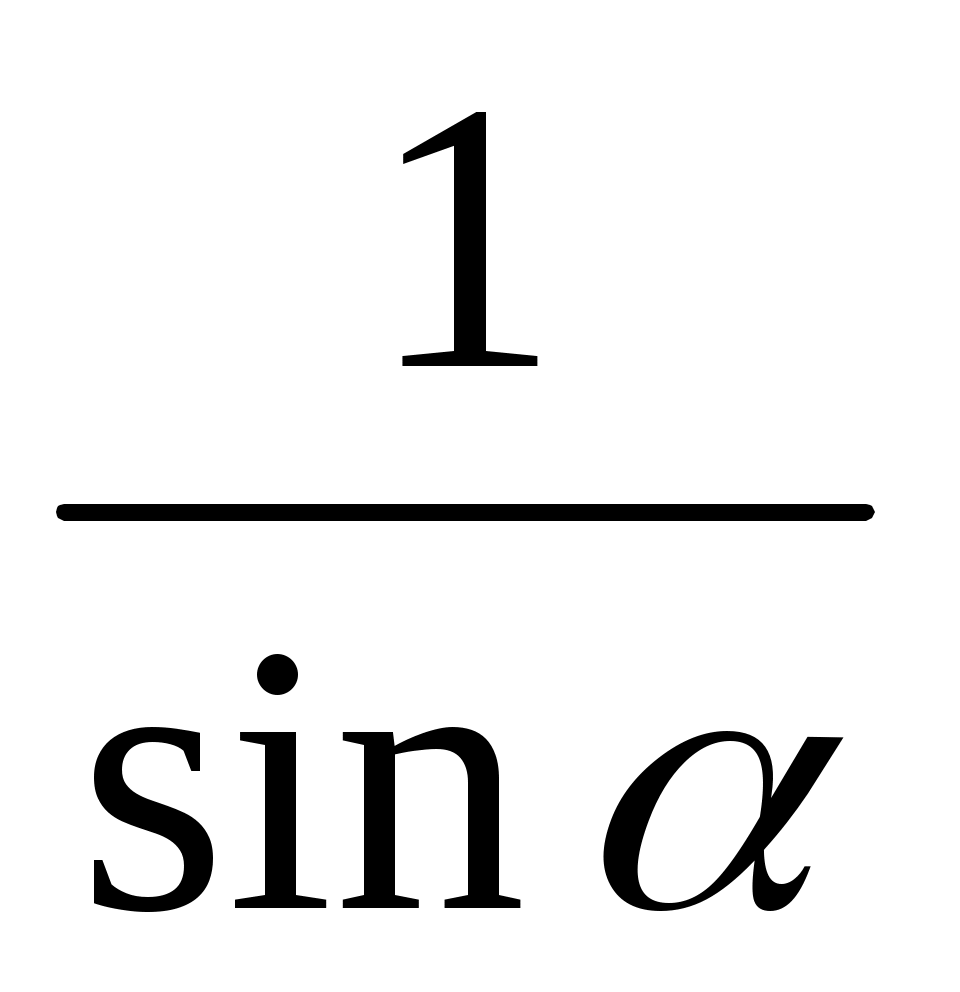
|
|
cos α
|
|
11
|
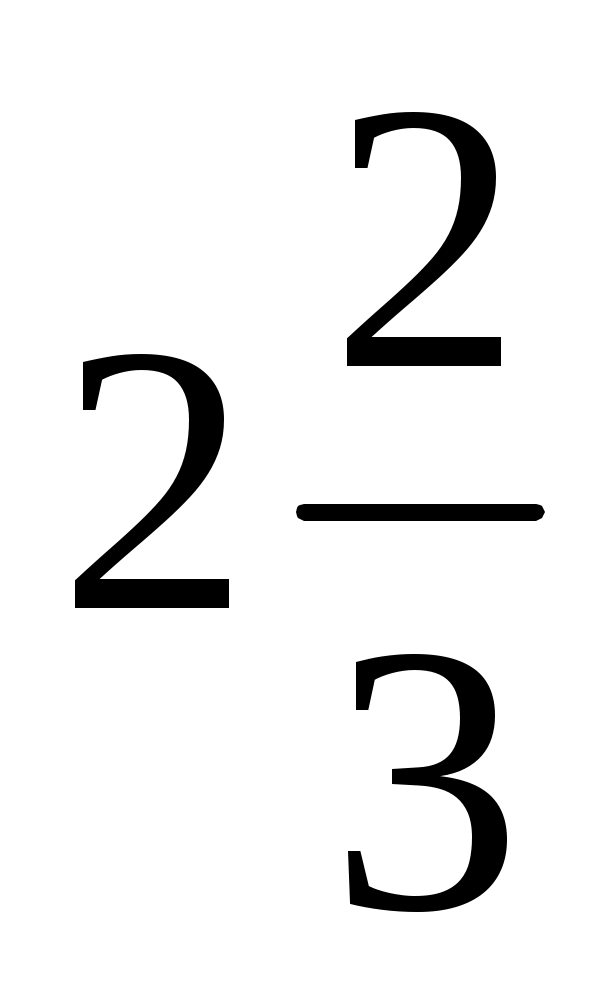
|
4
|
|
|
|
|
| Преподаватель предлагает проверить домашнее задание, выполненное на доске.
|
Выполняют на доске упражнения.
Устно выполняют задания и называют правильный ответ, находящийся в таблице.
Проверяют решения.
|
Мотивация.
Слово преподавателя:
- Итак, вы вспомнили изученный ранее материал. Эти знания вам пригодятся при дальнейшем изучении тригонометрии уже на этом уроке.
|
Отвечают и проверяют правильность своих ответов с помощью слайда 2.
|
Постановка учебной задачи.
Слово преподавателя:
- Кроме упражнений на дом вам было дано задание: вспомнить понятие тождества, тождественного выражения и тождественного преобразования. Сформулируйте определения этих понятий.

Слайд 2:
Тождеством называется равенство, справедливое при всех
допустимых значениях входящих в него букв.
Допустимые значения букв – это значения, которые могут принимать
буквы в данном выражении.
Выражения, находящиеся в левой и правой частях тождества,
называются тождественными.
Замена некоторого выражения другим, ему тождественным,
называется тождественным преобразованием данного выражения.
- Как вы думаете, как связаны эти понятия с изучаемым материалом?
(Предполагаемый ответ: тождества и тождественные выражения будут содержать тригонометрические функции, и мы будем преобразовывать такие выражения и доказывать тождества).
Преподаватель объявляет тему урока: «Тригонометрические тождества».
Планирование решения учебной задачи.
Слово преподавателя:
- При изучении темы «Зависимость между тригонометрическими функциями одного и того же аргумента мы уже встретились с тождествами. Например, это все формулы зависимости межу синусом, косинусом, тангенсом и котангенсом одного и того же угла. Сегодня мы выясним, как можно использовать эти формулы при упрощении тригонометрических выражений и доказательстве тригонометрических тожеств.
|
Предлагают варианты ответа.
Записывают тему урока в тетрадях.
|
II. Операционно-познавательная часть
|
Слово преподавателя:
- Напомните формулы зависимости между синусом и косинусом, тангенсом и косинусом, котангенсом и синусом, тангенсом и котангенсом.

Слайд 3:
sin2 α + cos2 α = 1 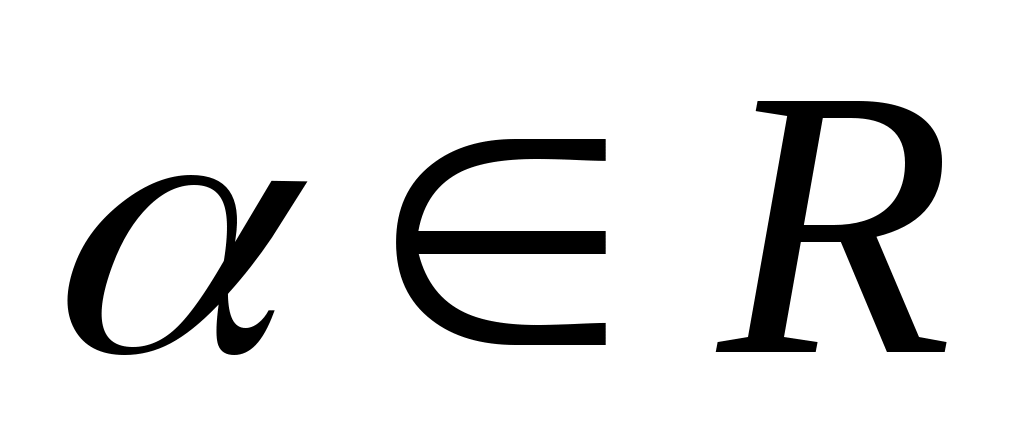
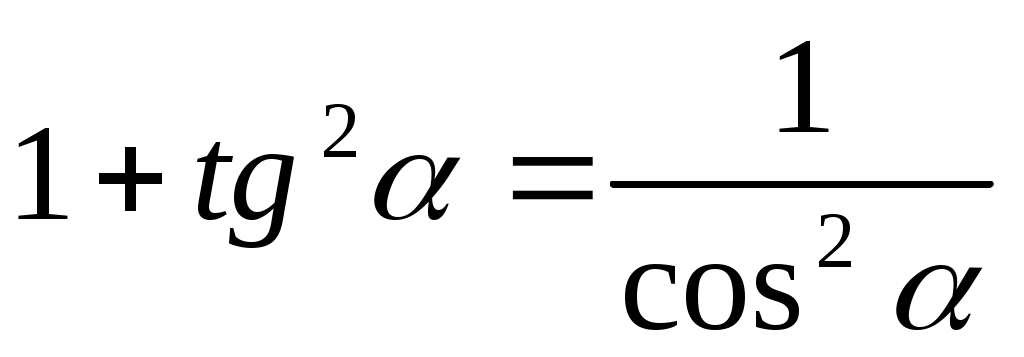 cos α ≠ 0, cos α ≠ 0, 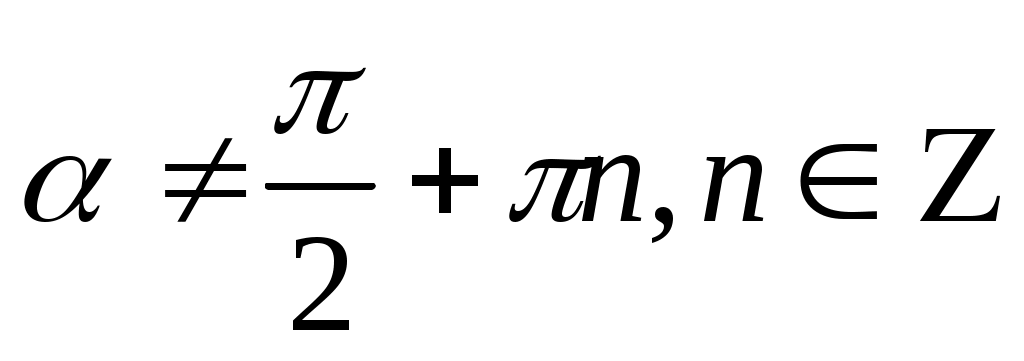
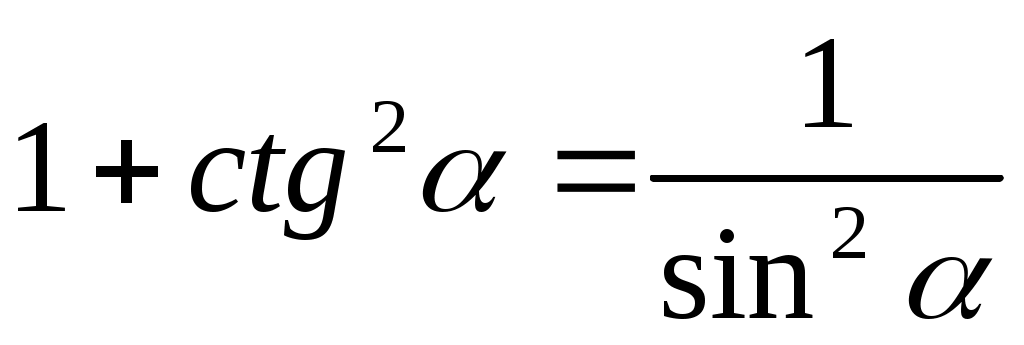 sin α ≠ 0, α ≠ πn, sin α ≠ 0, α ≠ πn,
tg α ∙ ctg α = 1 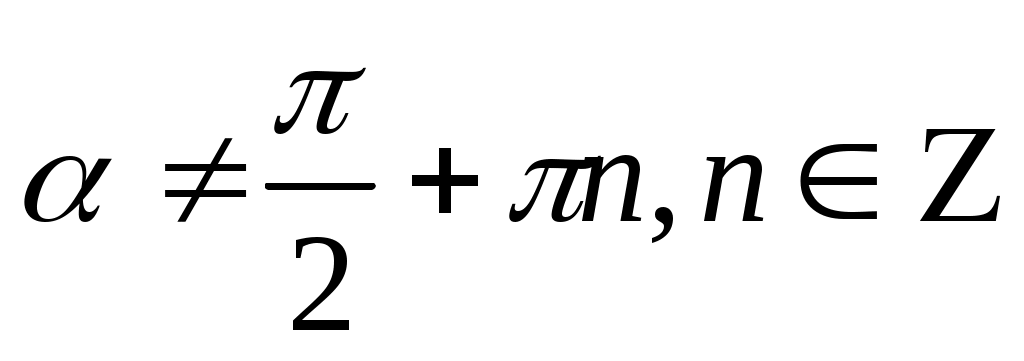 , , 
Преподаватель задаёт вопрос группе:
- При каких допустимых значениях α справедливы эти тождества?
Слово преподавателя:
- Для выполнения тождественных преобразований тригонометрических выражений можно использовать не только данные тригонометрические тождества, но и другие формулы тригонометрии, а также алгебраические преобразования, например, действия с дробями, вынесение за скобки общего множителя, формулы сокращённого умножения и т. д.
- Выполните следующие задания с помощью тождественных преобразований.

Слайд 4:
Упростите выражение:
а) 1 – sin2 x = cos2 x
б) cos2 β – 1 = – sin2 β
в) tg x ∙ ctgx + 4 = 5
г) cosα ∙ tgα = sinα
д) (1 – cos x)(1 + cos x) = 1 – cos2 x = sin2 x
е) sin2 α+ 2sinα ∙ cosα + cos2 α = (sinα + cosα)2
2. Выразите через sin2α:
a) (1 – cos2 α) + sin2 α = 2sin2 α
б) 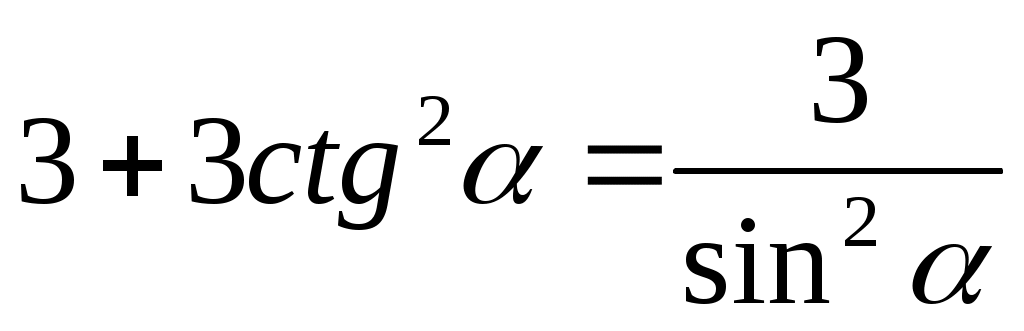
3) Выразите через tgα:
a) 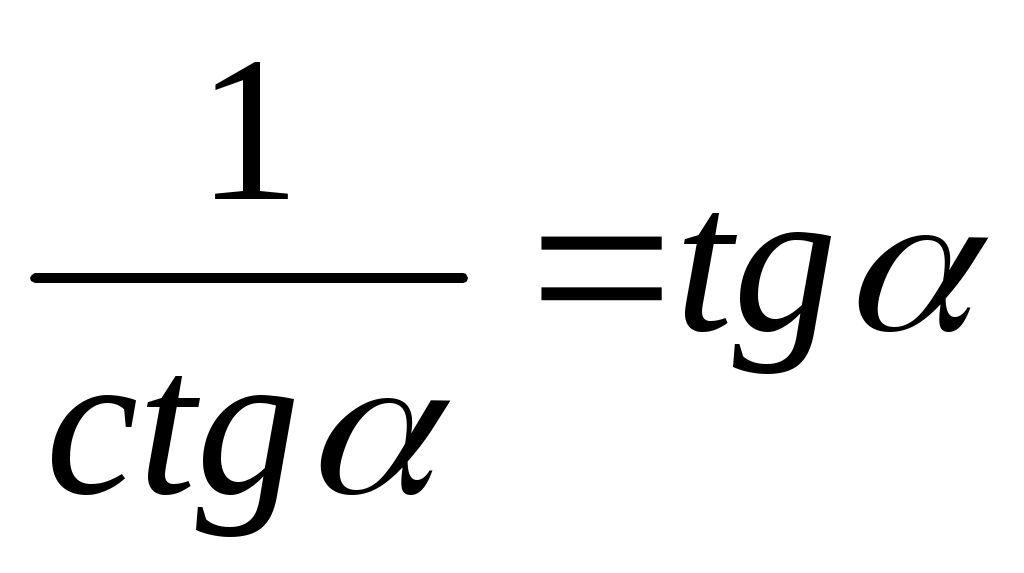
б) 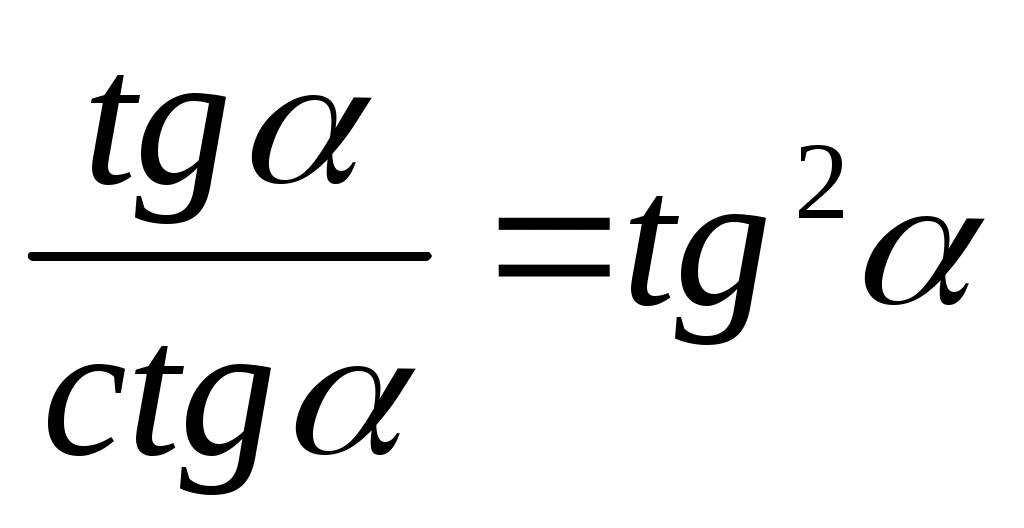
Слово преподавателя:
- Тождественные преобразования используются при доказательстве тождеств. Какие вы знаете способы доказательства тождеств?

Слайд 5:
Способы доказательства тождеств:
- преобразование правой части к левой;
- преобразование левой части к правой;
- установление того, что разность между правой и левой частями
равна нулю;
- преобразование левой и правой части к одному и тому же выражению.
Слово преподавателя:
- Рассмотрим задачи.

Слайд 6:
Задача 1. Доказать, что при α ≠ πn,  , справедливо равенство , справедливо равенство
sin2 α + ctg2 α + cos2 α = 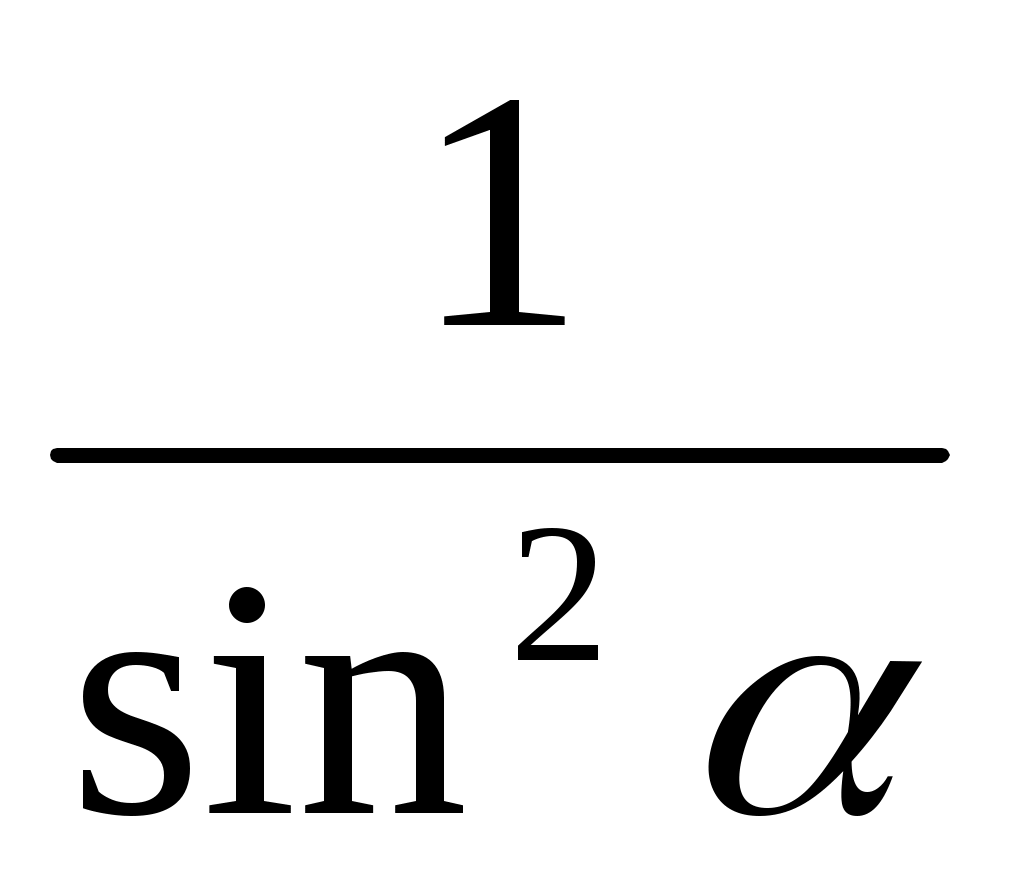
Доказательство:
sin2 α + ctg2 α + cos2 α = 1 + ctg2 α = 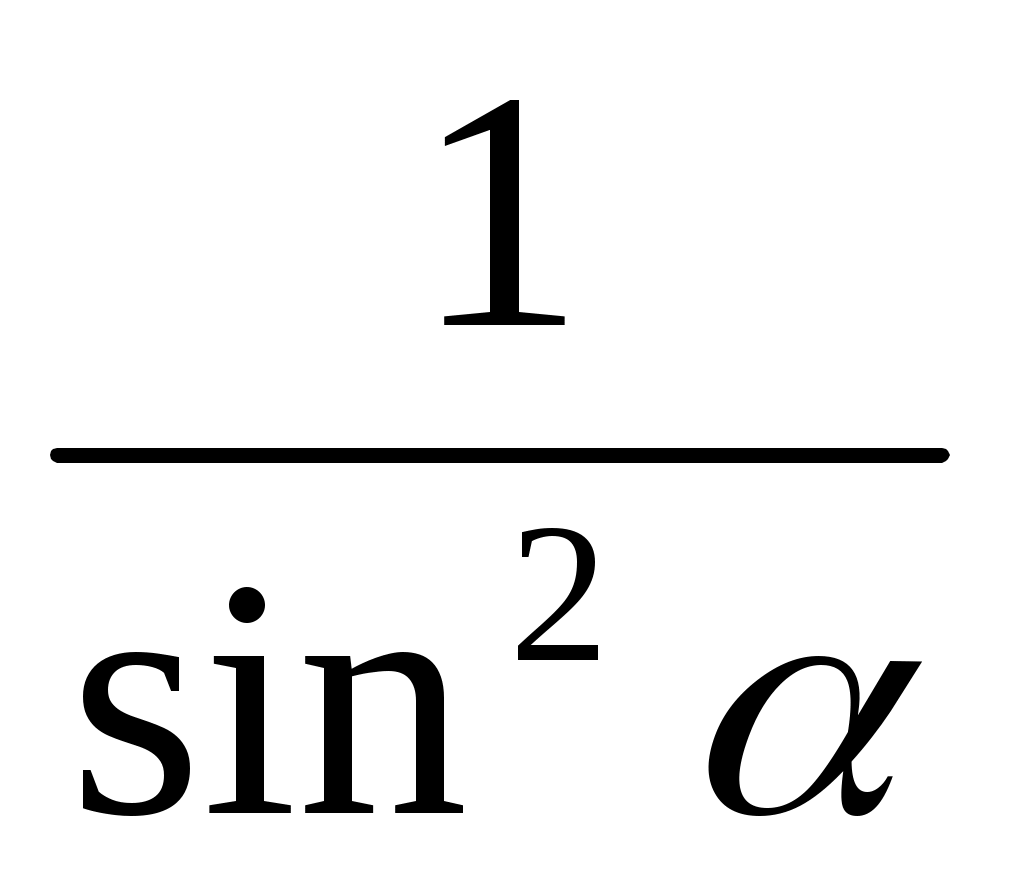
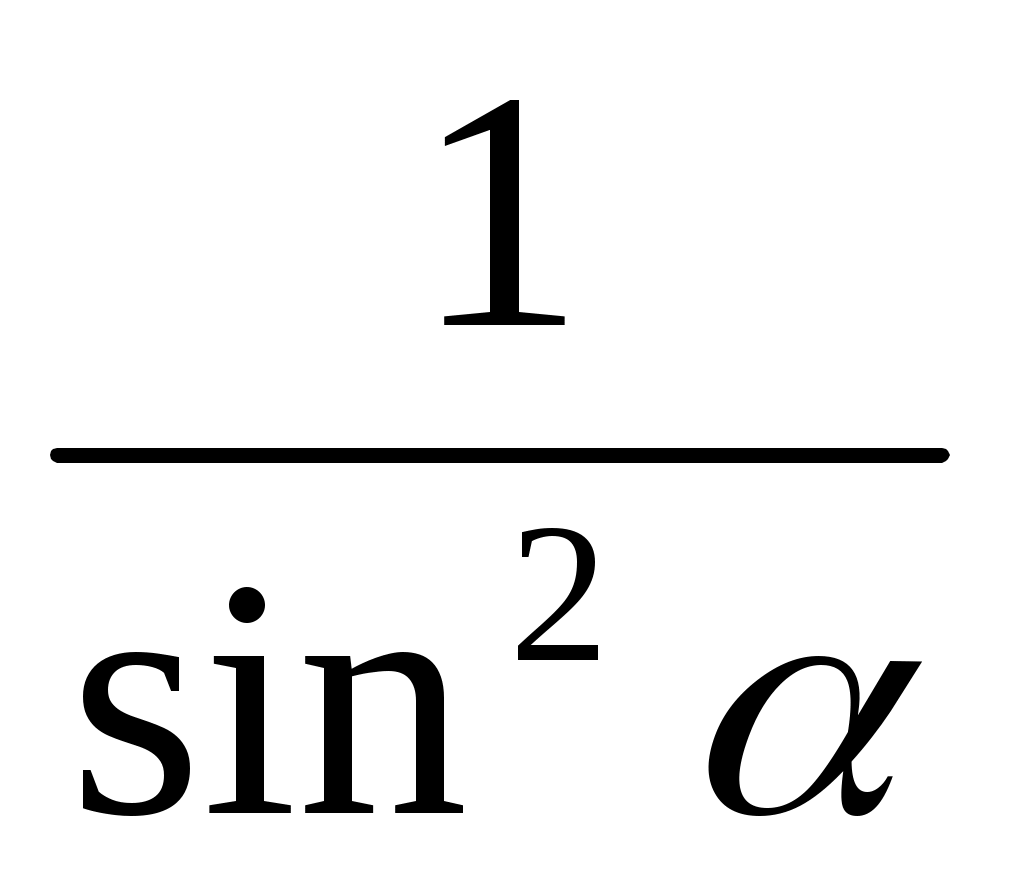 = = 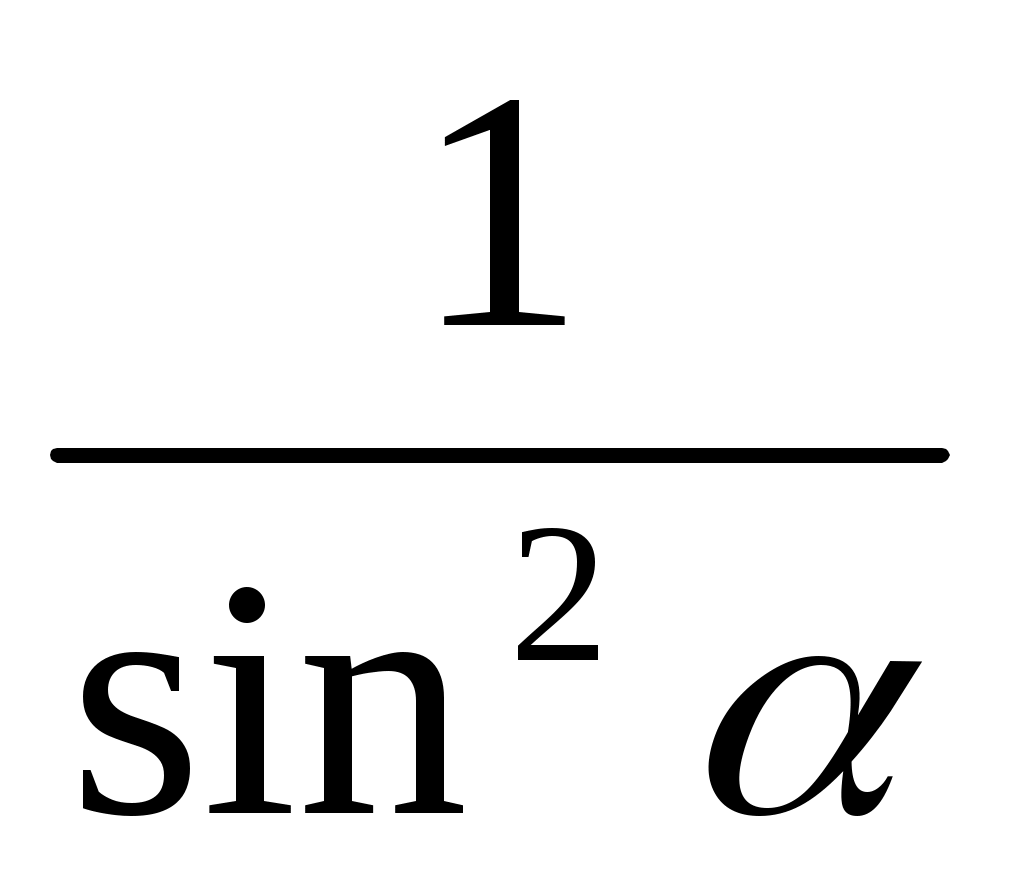
Что и требовалось доказать.
|
Называют формулы, при необходимости обращаются к упражнениям из домашнего задания.
При этом постепенно появляются формулы из левой части
слайда 3.
Называют допустимые значения α, при этом постепенно появляется правая часть слайда.
Отвечают. Правая часть равенства появляется при ответе учащихся.
Отвечают, проверяют ответы с помощью слайда 5.
Доказывают равенство с помощью преподавателя, записывают в тетрадь.
|

Слайд 7:
Задача 2. Доказать тождество cos2 α = (1 – sin α)(1 + sin α).
Доказательство:
(1 – sinα)(1 + sin α) = 1 – sin2 α = cos2 α
cos2α = cos2α
Что и требовалось доказать.
Преподаватель вызывает к доске двух учащихся.
Задача 3. Доказать тождество:
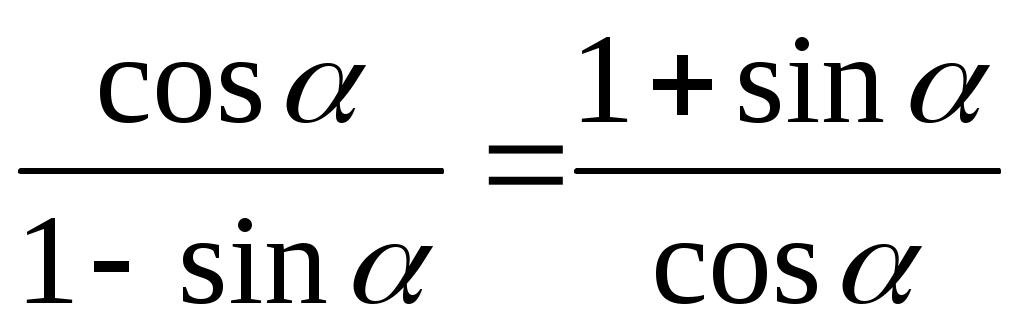
Доказательство:
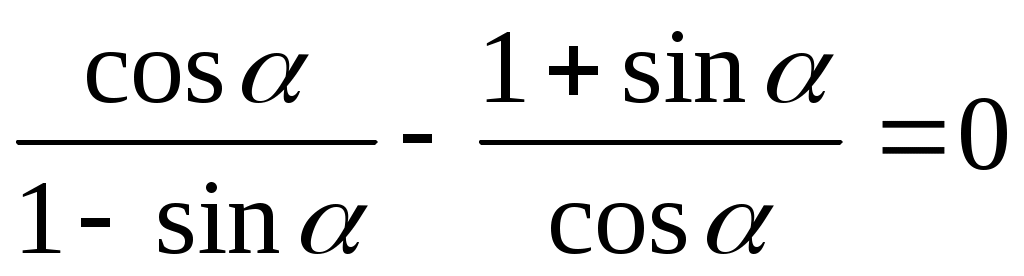
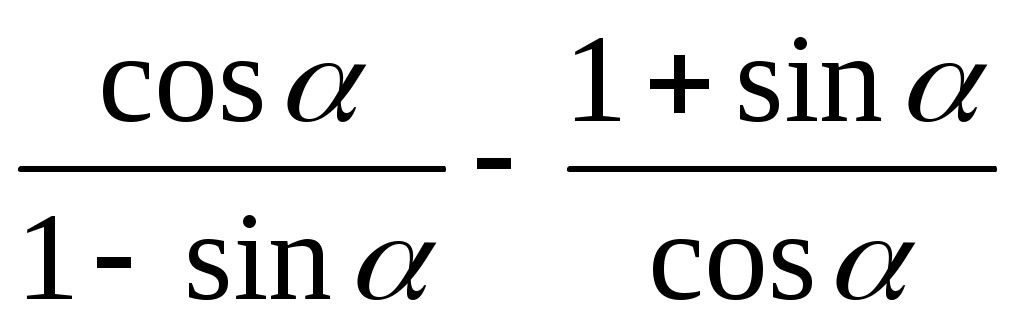 = =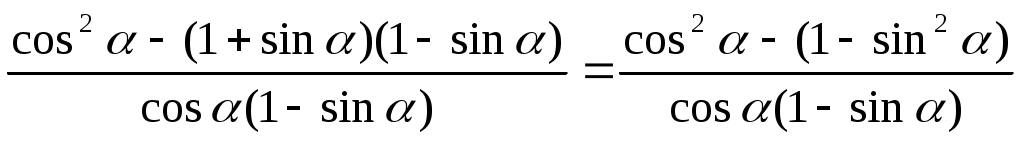 = =
= 
0=0. Что и требовалось доказать.
Задача 4. Доказать тождество:

Доказательство:
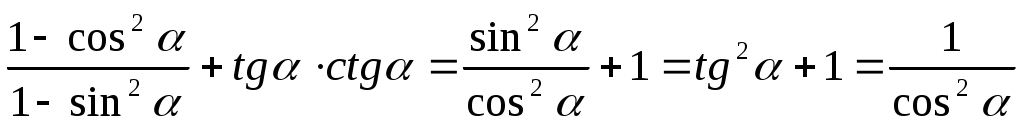


Что и требовалось доказать.
|
Устно проводят доказательство, затем записывают его в тетрадь.
Выполняют задачи 3 и 4 на закрытой части доски. Остальные самостоятельно решают эти задачи в тетрадях.
Проверяют решенные на доске и в тетрадях задачи.
|
III. Рефлексивно-оценочная часть
|
Слово преподавателя:
- Пришло время подвести итоги работы.
Преподаватель:
- Что вы сегодня узнали нового?
- Какова была цель вашей деятельности?
- Вы достигли поставленной цели?
- Что вы использовали, и что вам помогло в достижении цели?
Продолжите фразу:
«Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
«Сегодня на уроке я закрепил…»
-Все, кто отвечал на уроке будут оценены.
Преподаватель отмечает положительные и отрицательные моменты работы учащихся на уроке, типичные ошибки; выставляет и комментирует оценки.
В конце урока обучающимся предлагается написать синквейн на основе изученного материала.В этом выводе каждый студент соединяет и обобщает свои впечатления, знания, воображение.
|
|
Самостоятельная работа.
Вариант 1
|
Вариант 2
|
1.Упростите выражение:
tg cos cos
а) sin  б)ctg б)ctg  в)cos в)cos г)tg г)tg
2.Вычислите:
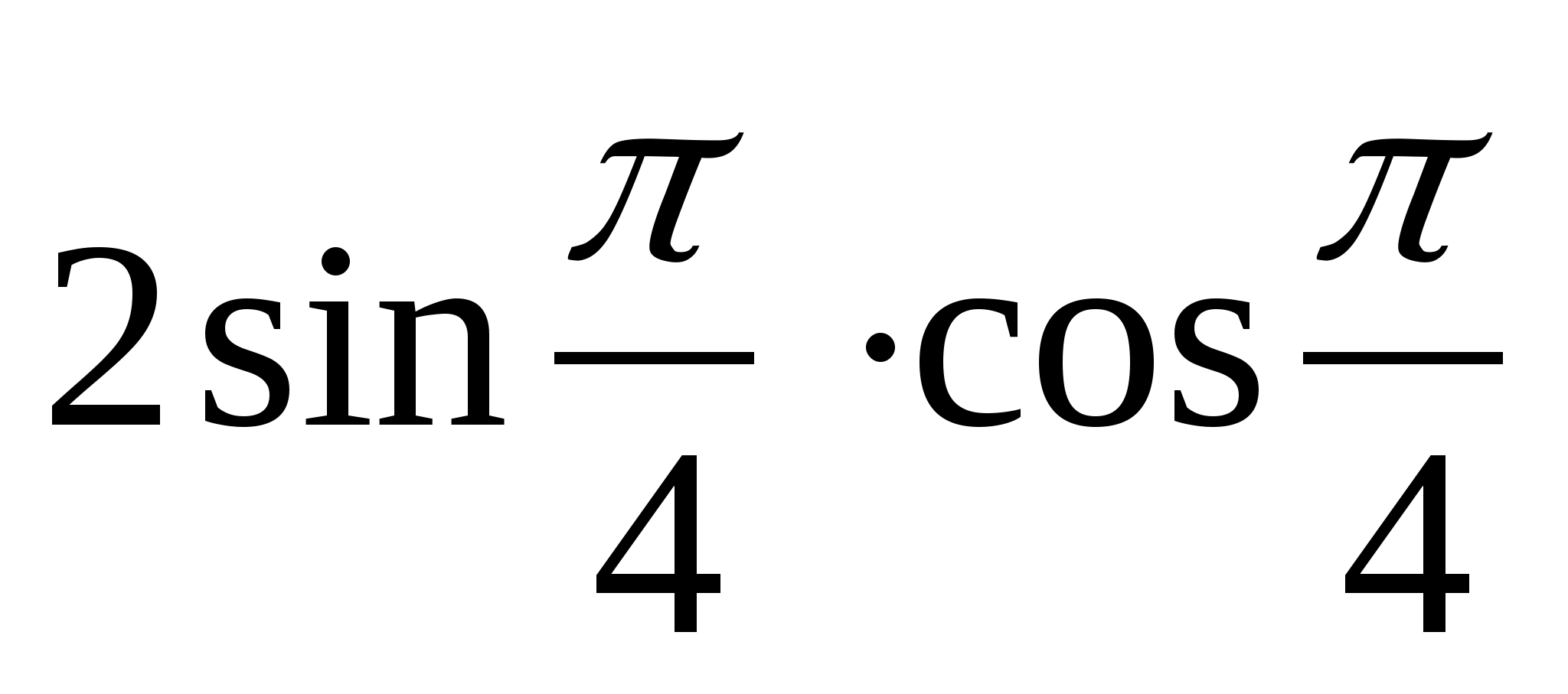
а)0 б) 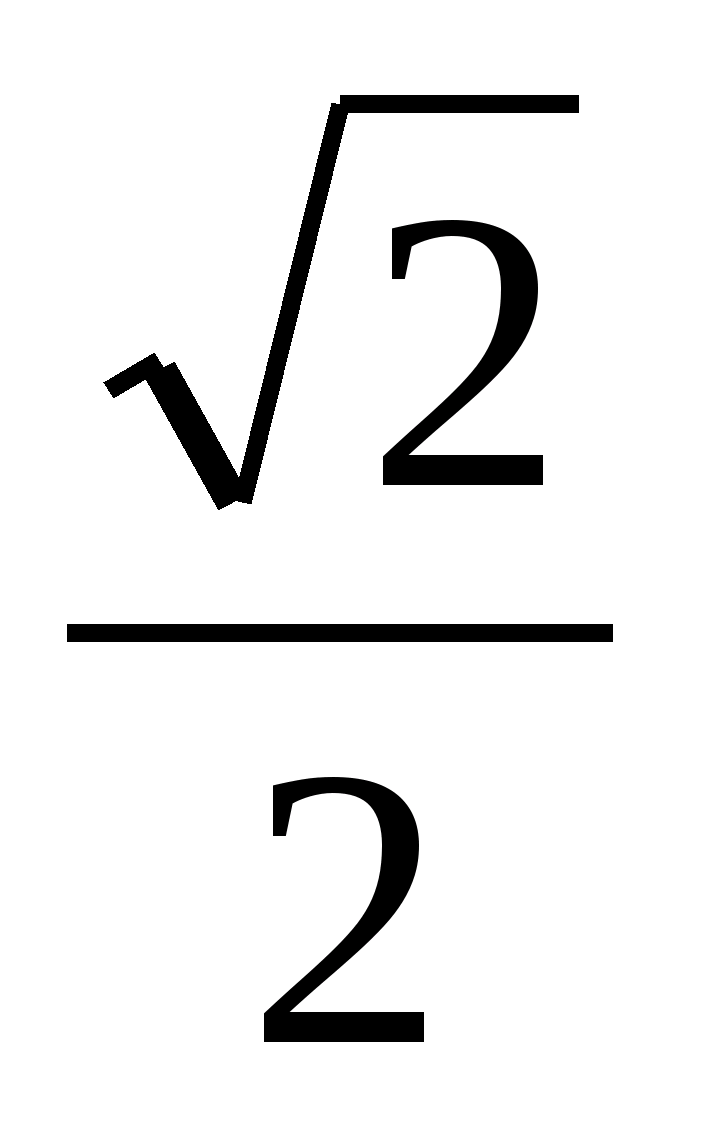 в)1 г) в)1 г)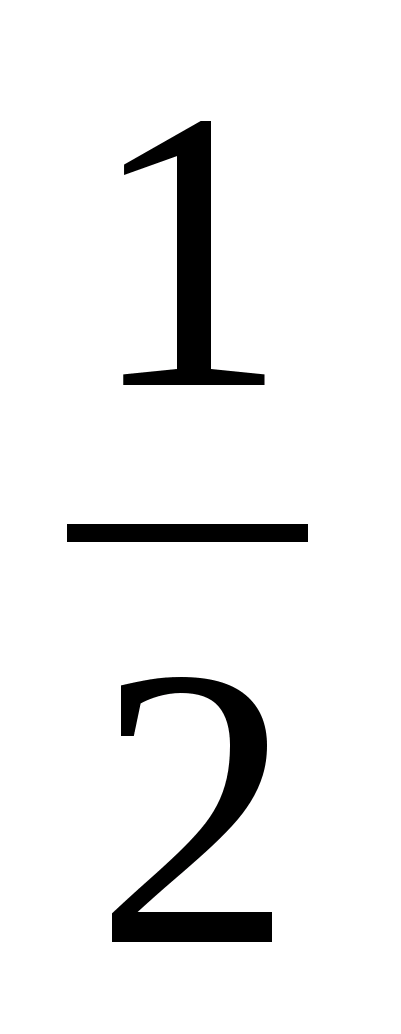
3.Решите уравнение:
sinx=1
а)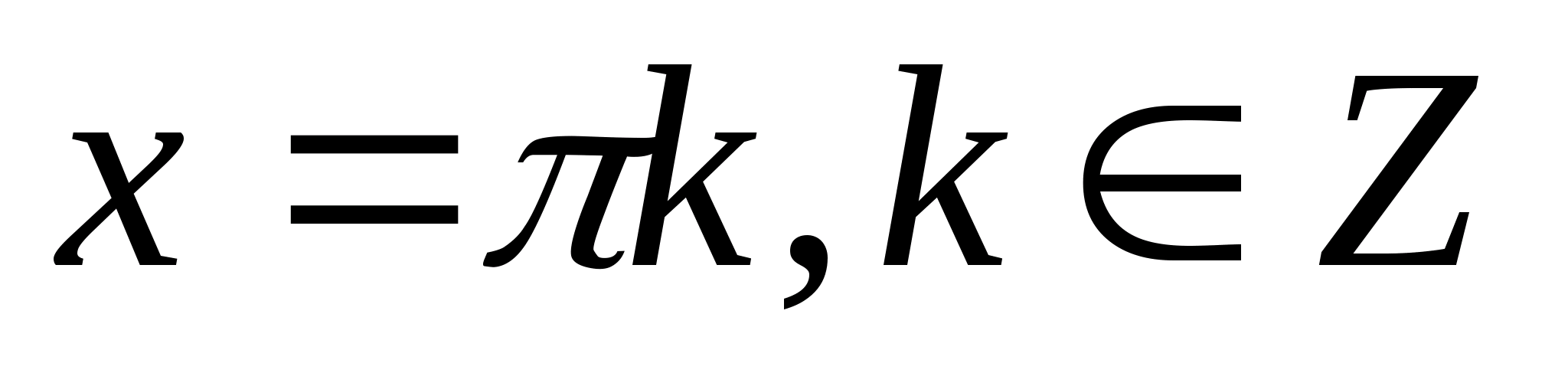 б) б)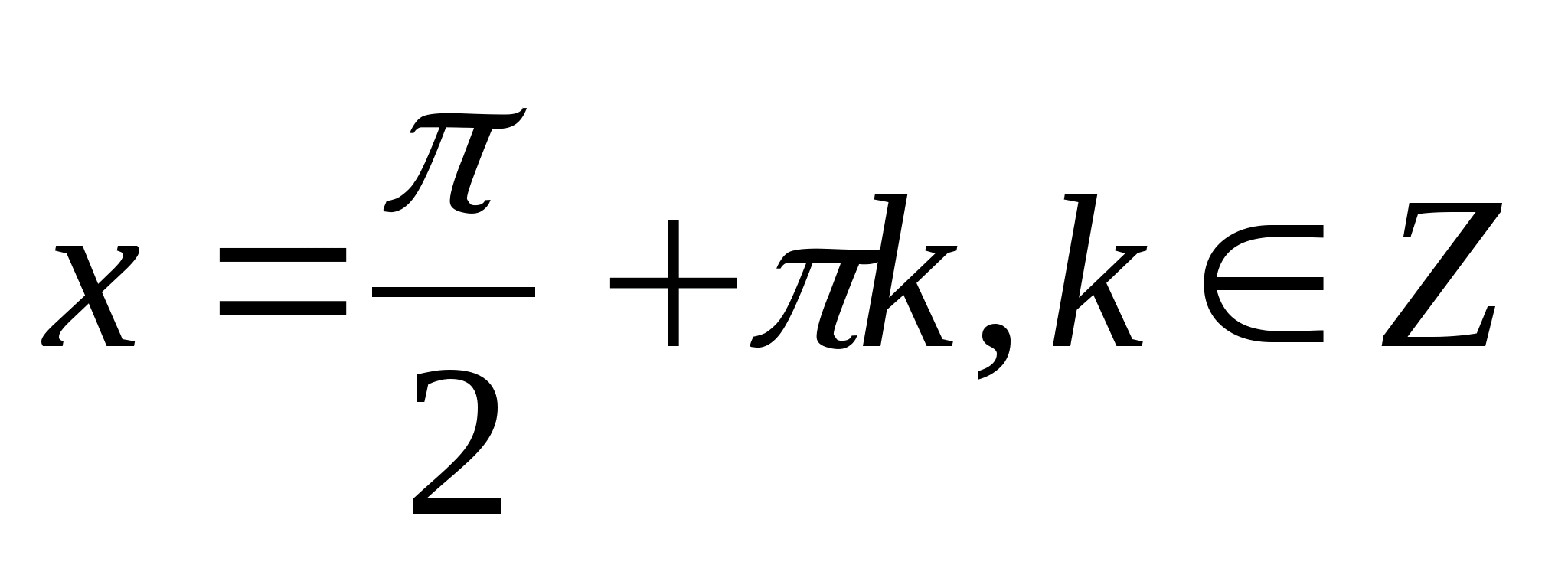 в) в)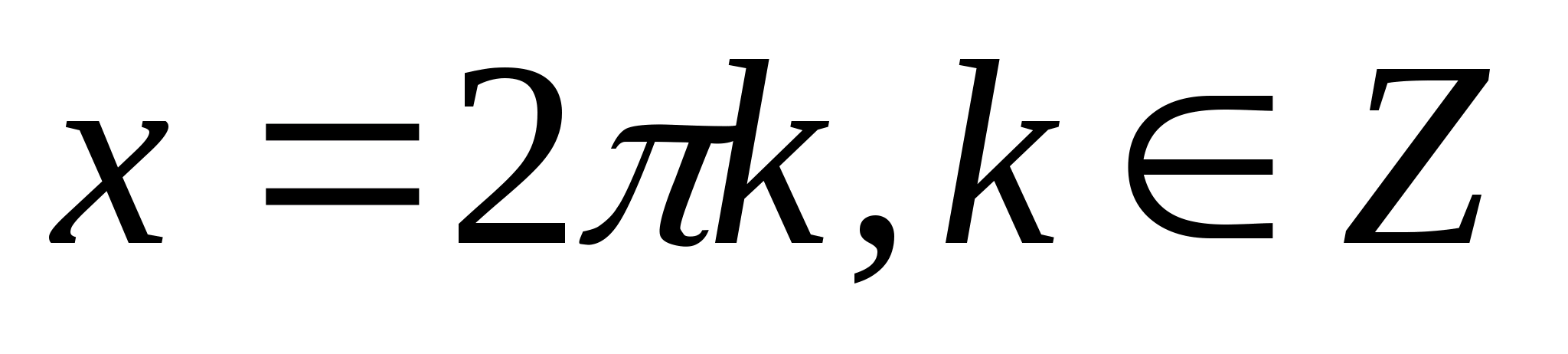 г) г) 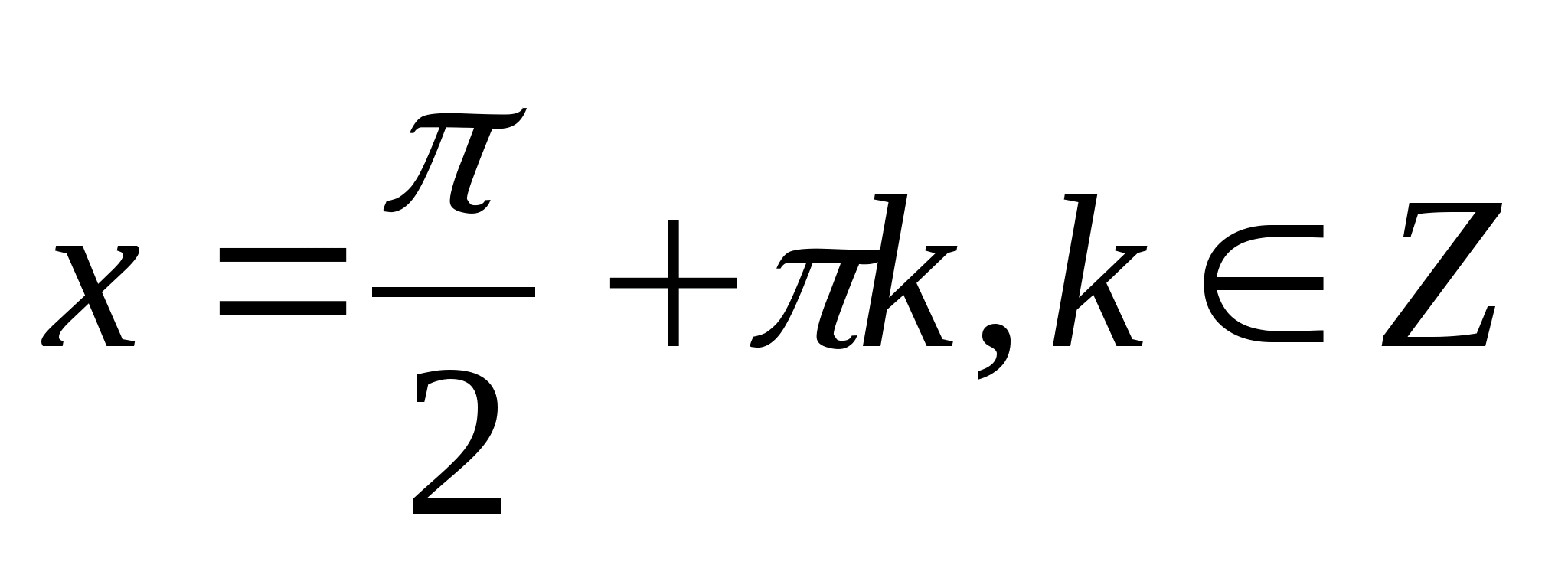 . .
4.Упростите выражение:

а)sin б)cos б)cos в)sin в)sin -cos -cos г) cos г) cos -sin -sin
5.Запишите решение.
Вычислите:
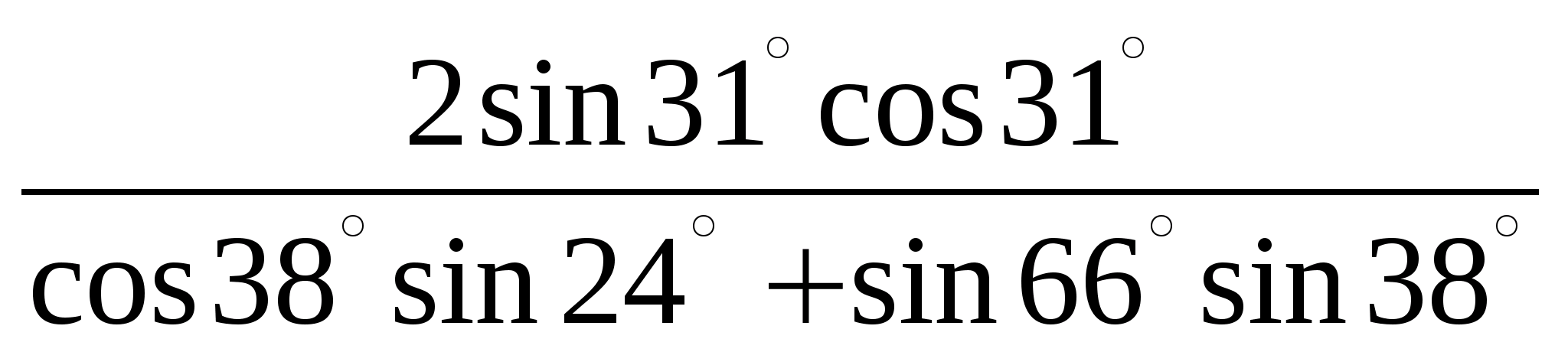
|
1.Упростите выражение:
ctg sin sin
а) sin  б)ctg б)ctg  в)cos в)cos г)tg г)tg
2.Вычислите:

а)0 б) 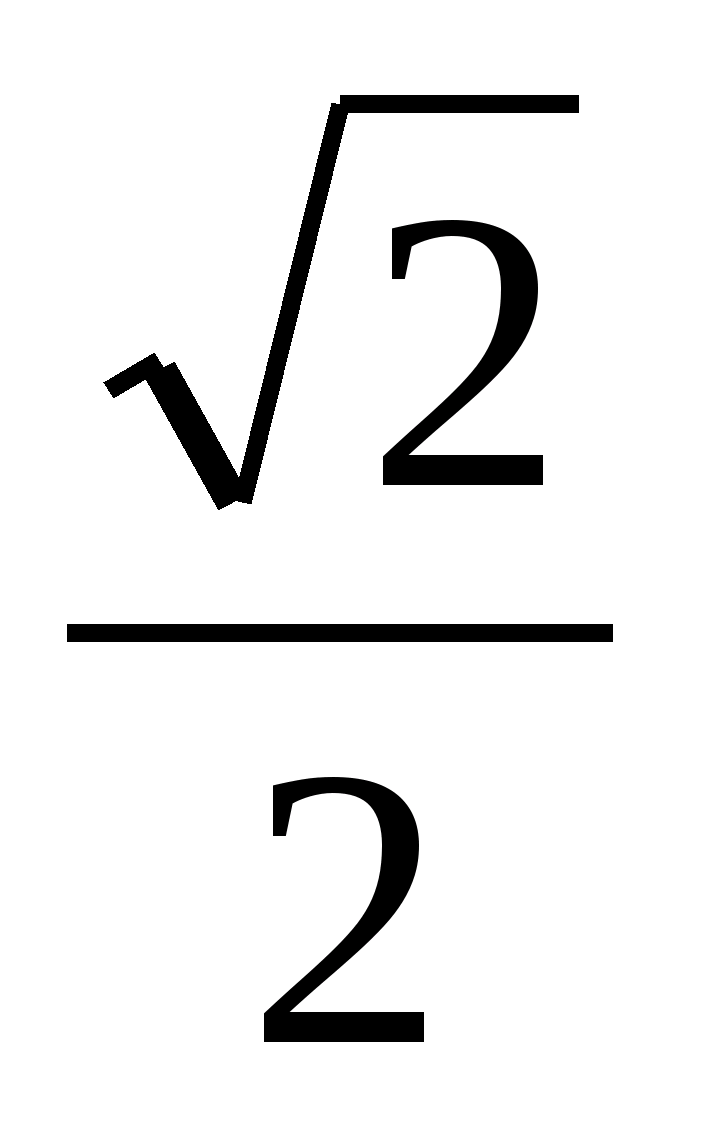 в)1 г) в)1 г)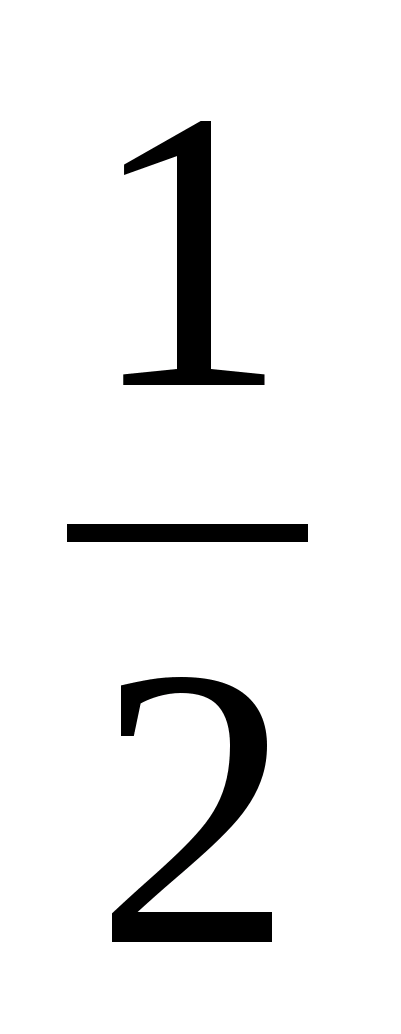
3.Решите уравнение:
cosx=1
а)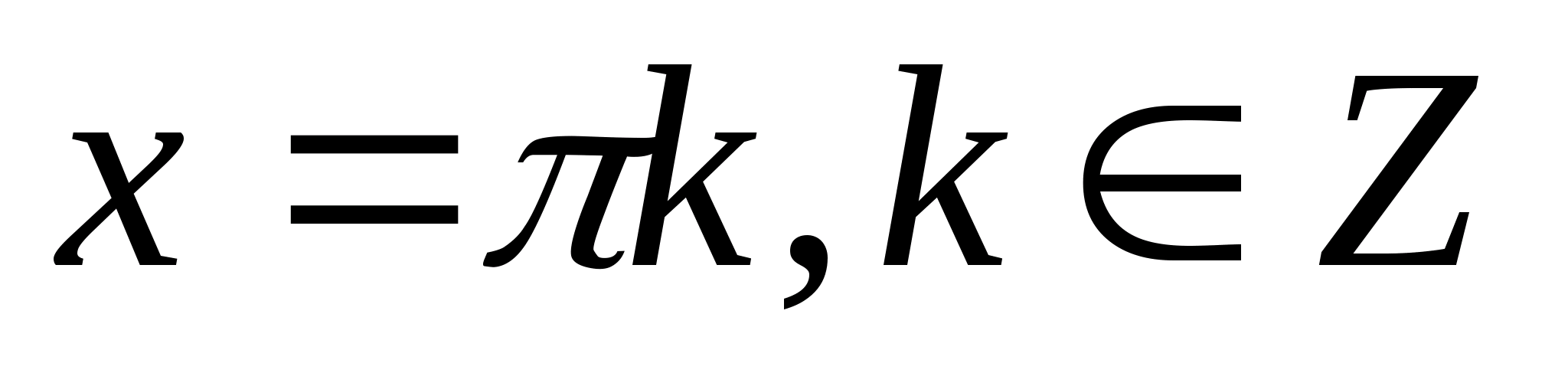 б) б)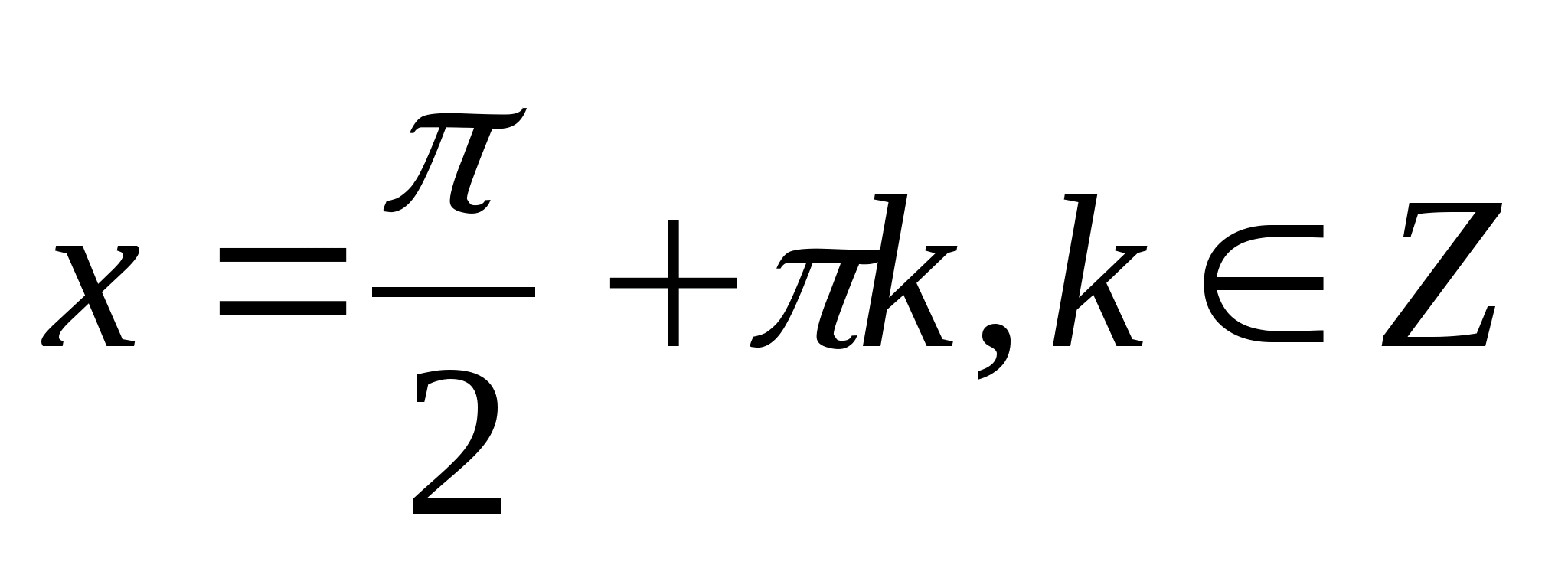 в) в)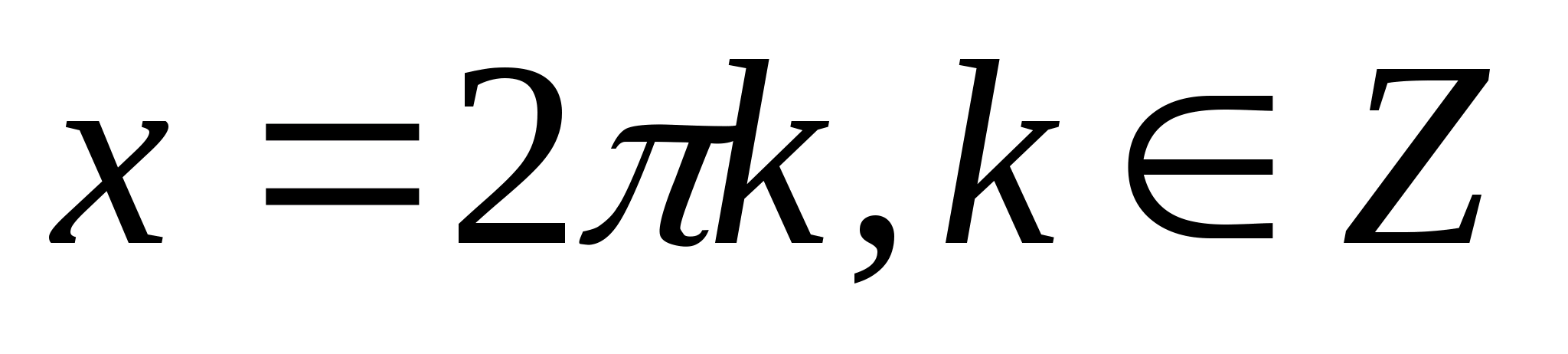 г) г)  . .
4.Упростите выражение:
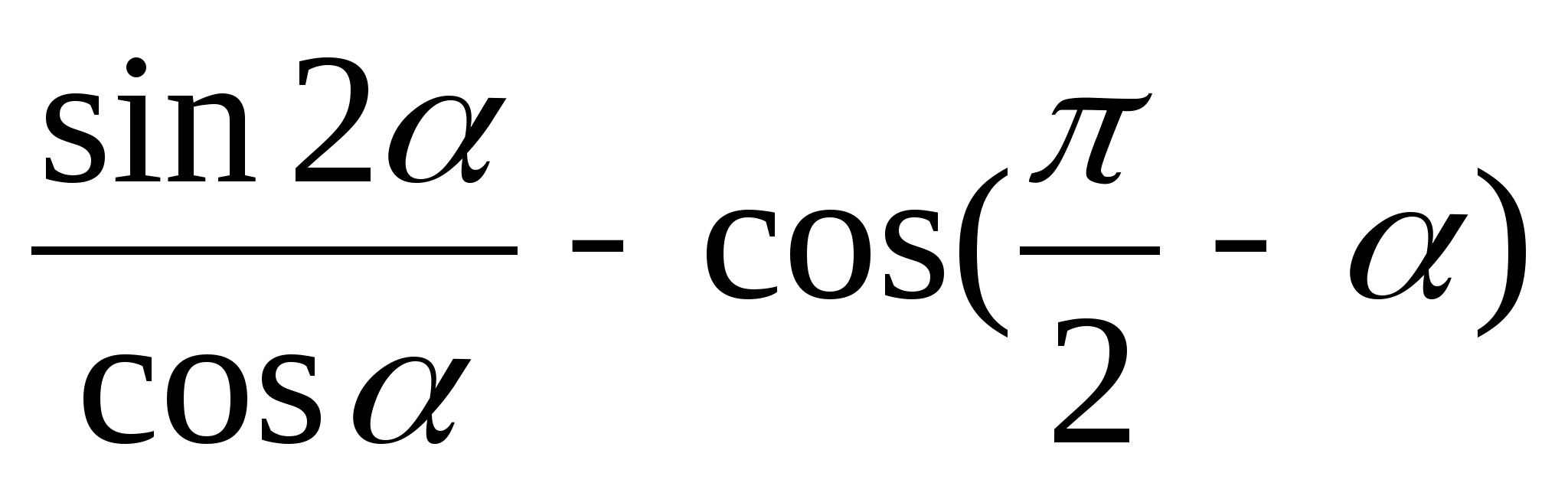
а)sin б)cos б)cos в)sin в)sin -cos -cos г) cos г) cos -sin -sin
5.Запишите решение.
Вычислите:
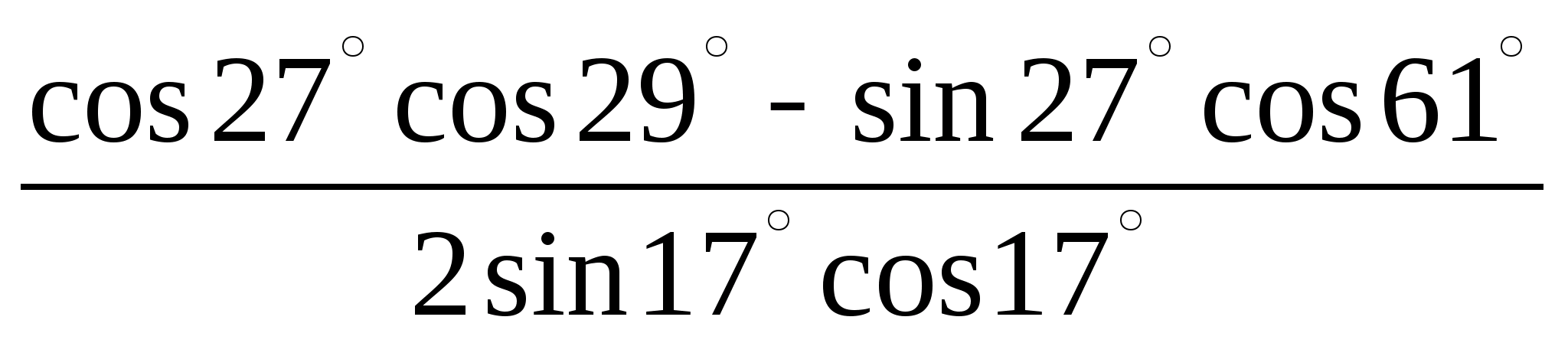
|
Итог урока.
Привести слова Ермакова В.П. «В математике следует помнить не формулы, а процессы мышления».
Домашнее задание: «Проверь себя» страница 130.
Литература.
1.Математика. В.Н.Богомолов. Москва, «Просвещение», 2018.
2.Устные упражнения по алгебре и началам анализа. Р.Д. Лукин и другие.
3.Дидактические материалы по алгебре и началам анализа. Б.М .Ивлев и другие.
4.Дидактические материалы по алгебре и началам анализа. Л.О. Денищева и другие.
5.Единый Государственный Экзамен. Тестовые задания. Математика. 2016г., С.В. Климин и другие.
САМОАНАЛИЗ УРОКА ПО МАТЕМАТИКЕ
В группе 15 ЖКХ по ТЕМЕ
«Тригонометрические тождества»
В группе – 25 студентов, средний уровень обучаемости, в нем есть сильные ребята и очень слабые. Но большинство учащихся настроены на учебу и стараются усвоить весь изучаемый материал. При подготовке занятия учитывалась эта особенность группы.
Так как в колледже занятия включает в себя пару уроков , то первая часть – урок- включал объяснение материала; а второй урок являлся уроком закрепления и обобщения в главе «Элементы тригонометрии». Тема очень важная и используется и на других предметах при изучении геометрии, физики, химии, информатики.
На проведение урока были поставлены следующие цели
Образовательная: формирование понятия тождества, умения доказывать тождества и упрощать тригонометрические выражения с использованием изученных формул.
Развивающая: развитие логического мышления, памяти, умений сравнивать, выявлять закономерности, преодолевать трудности при решении математических задач, развитие познавательного интереса учащихся.
Воспитательная: воспитание ответственного отношения к учебному труду, настойчивости для достижения конечных результатов при решении задач.
А также задачи
Образовательные:
-Закрепление навыков и умений для преобразования тригонометрических выражений;
Развивающие:
-Развитие логического мышления, внимания;
-Развитие коммуникативных качеств;
-Развитие математической речи;
-Развитие интереса к предмету;
Воспитательные:
-Воспитание чувства взаимопомощи и товарищества;
-Привитие навыков дружеского общения;
-Формирование положительного отношения к учебе.
Я считаю, что структура урока была выбрана рационально для изучения и закрепления темы и учитывая индивидуальные особенности обучающихся. Применялись различные методы работы
- деятельный (процесс познания идет от обучающихся),
- наглядно – демонстративный,
- частично – поисковый (учим детей наблюдать, анализировать, сравнивать, делать выводы и обобщения под руководством преподавателя),
- практический
Актуализация знаний началась с создания проблемной ситуации, которая подвела обучающихся к цели и задачам урока. В ходе вопросно – ответной беседы студенты включились в коллективную деятельность.
Используя наглядно – демонстративный метод обучения, студенты имели возможность высказывать свои мнения, выслушать своих товарищей, проявлять познавательную активность, делать выводы. Данный этап проходит в форме диалога между мной преподавателем и обучающимися. Наводящие вопросы позволяли моим ученикам двигаться в правильном направлении и подойти к обобщению новых знаний.
В повторение знаний использовался частично – поисковый, практические методы обучения. В ходе коллективной деятельности студенты учились анализировать, сравнивать, обобщать и делать выводы.
Закрепление изученного материала предполагало продолжение работы для достижения поставленных задач урока. Математическая речь, логическое мышление, умение работать самостоятельно не у всех обучающихся получалось. Обучающиеся владеют уже необходимыми знаниями. Работа в парах, выполнялась каждым студентом индивидуально и с взаимной проверкой (объяснением) в парах. Это позволило мне выделить уровни усвоения материала обучающимися и создать ситуацию успеха. На протяжения всего занятия поддерживалась атмосфера доброжелательности, работоспособности и взаимовыручки. Переключения с одной деятельности на другую обеспечило предупреждения перегрузки обучающихся в течение всего урока. Обучающиеся применяли полученные знания на уроке, была проведена рефлексия. |
|
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.






