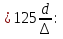Лекция 5. Турбулентный режим. Общая картина течения. Осредненная скорость. Профиль осредненной скорости по сечению турбулентного потока жидкости. Структура профиля
 Скачать 56.41 Kb. Скачать 56.41 Kb.
|
|
Лекция 5 Турбулентный режим. Общая картина течения. Осредненная скорость. Профиль осредненной скорости по сечению турбулентного потока жидкости. Структура профиля. При турбулентном режиме струйность (слоистость) потока нарушается. Траектория жидкой частицы представляет собой сложную кривую, в данной точке русла скорость каждой частицы меняется во времени по величине и направлению. В самом деле, пусть имеется неподвижная точка пространства рассматриваемого потока жидкости А; пусть жидкая частица М1, двигаясь по некоторой сложной извилистой траектории, приходит в точку А в момент времени  со скоростью со скоростью 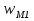 . Через элементарный промежуток времени . Через элементарный промежуток времени 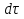 , т.е. в момент времени , т.е. в момент времени 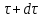 , двигаясь уже по другой траектории, в ту же точку А приходит другая жидкая частица М2, имеющая в этой точке скорость , двигаясь уже по другой траектории, в ту же точку А приходит другая жидкая частица М2, имеющая в этой точке скорость  , которая отличается от скорости , которая отличается от скорости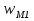 как по величине так и по направлению как по величине так и по направлению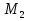  A      • Турбулентный режим нестационарен по своей природе. Скорости 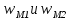 называют мгновенными местными скоростями. Всякую такую скорость можно разложить на три взаимно перпендикулярные скорости: продольную – параллельную общему направлению потока называют мгновенными местными скоростями. Всякую такую скорость можно разложить на три взаимно перпендикулярные скорости: продольную – параллельную общему направлению потока 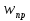 и две поперечные, лежащие в плоскости живого сечения потока. и две поперечные, лежащие в плоскости живого сечения потока.Принято анализировать поведение скорости жидкости при турбулентном режиме по продольной составляющей скорости. T  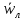 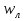   Проследим за продольной составляющей скорости 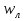 за несколько одинаковых промежутка времени Т0 большой длительности. Для каждого участка времени можно рассчитать осредненную скорость продольной составляющей за несколько одинаковых промежутка времени Т0 большой длительности. Для каждого участка времени можно рассчитать осредненную скорость продольной составляющей 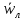 (средняя по времени T0 скорость в данной точке турбулентного потока) по формуле (средняя по времени T0 скорость в данной точке турбулентного потока) по формуле Отклонение истинной скорости в данной точке от осредненной называется пульсацией скорости. Как видно из рисунка пульсация скорости знакопеременна. Если значения осредненной скорости на каждом из участков сохраняет свою величину, т.е. не зависит от времени, то такое турбулентное течение называется установившимся, тогда этой величиной можно оперировать как локальной скоростью и использовать для него уравнение Бернулли и другие уравнение справедливые для стационарного потока. Наряду с осредненной скоростью при турбулентном режиме осредняются и другие величины: давление, ускорение, плотность и т.д. Значит возможен анализ турбулентного потока как стационарного. Ламинарный подслой Турбулентный пограничный слой Ядро турбулентного потока 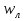 Профиль осредненной скорости по сечению турбулентного потока. Структура профиля. Профиль трансформируется в зависимости от критерия Рейнольдса. Чем выше значение Re, тем ближе профиль к вертикальной линии и тем меньше толщина ламинарного подслоя. Профиль скорости можно характеризовать отношением:  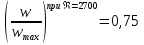  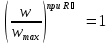 Однако профиль скоростей при турбулентном режиме описать математически невозможно, и аналитически найти выражение для коэффициента гидравлического сопротивления Г не представляется возможным. Поэтому поиск расчетного выражения для коэффициента гидравлического сопротивления Г при турбулентном режиме базируется на эксперименте. Движение жидкости в трубах с шероховатой поверхностью. Расчет коэффициента гидравлического сопротивления при турбулентном режиме движения жидкости. До сих пор как при рассмотрении вопросов, связанных с ламинарным течением, так и с турбулентным, ничего не говорилось о шероховатости поверхности труб и ее влияния на потерю энергии движущейся жидкости. Однако трубопроводы всегда обладают в той или иной степени неровностями на внутренней поверхности и поэтому не являются гладкими. В гидравлике при решении вопроса о шероховатости стенки играет большую роль ламинарный подслой, или так называемая ламинарная пленка. Обозначим абсолютный выступ шероховатости через  . Если при движении жидкости в трубе ламинарная пленка полностью покрывает выступы шероховатости, т.е если . Если при движении жидкости в трубе ламинарная пленка полностью покрывает выступы шероховатости, т.е если  , то, с точки зрения гидравлики, труба рассматривается как гладкая (гидравлически гладкая). Однако с повышением числа Re толщина ламинарной пленки уменьшается. При достижении некоторого значения числа Рейнольдса бугорки шероховатости начнут разрывать ламинарную пленку и, вызывая дополнительные возмущения в потоке, будут влиять на величину потери энергии движущейся жидкости. , то, с точки зрения гидравлики, труба рассматривается как гладкая (гидравлически гладкая). Однако с повышением числа Re толщина ламинарной пленки уменьшается. При достижении некоторого значения числа Рейнольдса бугорки шероховатости начнут разрывать ламинарную пленку и, вызывая дополнительные возмущения в потоке, будут влиять на величину потери энергии движущейся жидкости.Обычно, при обработки опытных данных шероховатость определяется не абсолютным значением выступа шероховатости, а отношением его к внутреннему диаметру трубы 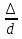 . Это относительная шероховатость (степень шероховатости . Это относительная шероховатость (степень шероховатости  ) )В области турбулентного течения можно выделить три зоны.
Формула Блазиуса : 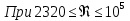 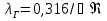 Формула Никурадзе для Re 105 3,4106 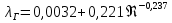
Рекомендуется формула Альтшуля для 2320 < Re < 218 d/: 
Общий график зависимости 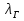 от критерия Рейнольдса и от степени шероховатости показан на рисунке от критерия Рейнольдса и от степени шероховатости показан на рисункеРис. Зависимость коэффициента гидравлического сопротивления от критерия Рейнольдса. 1 – ламинарный режим, формула 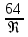 ; 2 – зона гладкостенного сопротивления, формулы Блазиуса и Никурадзе; 3 – зона шероховатого трения, формула Альтшуля; 4 - зона вполне шероховатого трения, формула Шифринсона. ; 2 – зона гладкостенного сопротивления, формулы Блазиуса и Никурадзе; 3 – зона шероховатого трения, формула Альтшуля; 4 - зона вполне шероховатого трения, формула Шифринсона.2 турб. реж. перех. реж. ламин. реж.  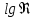  1 3 4 Местные потери энергии движущейся жидкости. Местные сопротивления. В уравнении Бернулли, записанном для потока вязкой жидкости 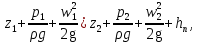 слагаемое 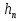 , стоящее в правой части, содержит в себе как потери на трение (путевые потери), так и потери энергии, идущие на преодоление местных сопротивлений. , стоящее в правой части, содержит в себе как потери на трение (путевые потери), так и потери энергии, идущие на преодоление местных сопротивлений. Местными сопротивлениями называются сопротивления движению, возникающие в потоках жидкости на участках резкого изменения конфигурации потока, например при резком сопряжении труб различных диаметров, при различного рода поворотах, в местах присоединения вентилей, задвижек, клапанов и т.д. При прохождении жидкости через участки с местными сопротивлениями энергия жидкости теряется на изменение направления и перераспределение скоростей, на возникающие вихреобразования и срывы потока, сопровождающиеся бурным перемешиванием между частицами жидкости и интенсивном обменом количества движения. Местные потери энергии вычисляются по формуле 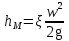 , где , где 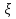 - коэффициент местного сопротивления (справочная величина в зависимости от вида местного сопротивления, геометрических размеров и Re), w – бо'льшая скорость участка местного сопротивления. Если на рассматриваемом участке трубопровода одного диаметра имеется несколько местных сопротивлений, тогда, согласно принципу наложения потерь, местные потери представляют собой сумму - коэффициент местного сопротивления (справочная величина в зависимости от вида местного сопротивления, геометрических размеров и Re), w – бо'льшая скорость участка местного сопротивления. Если на рассматриваемом участке трубопровода одного диаметра имеется несколько местных сопротивлений, тогда, согласно принципу наложения потерь, местные потери представляют собой сумму 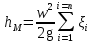 , где n – число местных сопротивлений. , где n – число местных сопротивлений.Примечание: принцип наложения потерь справедлив при условии, если местные сопротивления находятся друг от друга на расстоянии не менее 20 диаметров трубы. Общие потери энергии движущейся жидкости. Общие потери энергии движущейся жидкости в трубопроводе одного диаметра рассчитываются по формуле  + + . .Расчет простого трубопровода. При расчете простого трубопровода решают две задачи:
Дано H, V, l. Найти: диаметр трубопровода.
Дано l, d, H(V). Найти V(H). 0 P1 f1 w1 P2 f2 w2 w V V z2 z1 l, d, Г h f 1 1 2 2 0 Чтобы вывести формулу для решения любой из поставленных задач, воспользуемся уравнением Бернулли для вязкой жидкости:  дополняем уравнением сплошности: 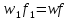 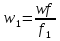 отношение f/f1 0, так как Sтруб-да<  тоже самое и с w2: 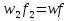  отношение f/f2 0, так как fтруб-да<   Правую часть уравнения называют суммарный располагаемый гидростатический напор (H).  Итак, получаем первую основную формулу для расчета простого трубопровода: 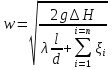 где n – число местных сопротивлений. 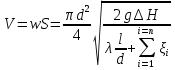 Пусть p1 = p2, тогда H = h – высота “подъема” жидкости (расстояние между первым и вторым сечениями потока жидкости). Алгоритм расчета задачи проектирования:
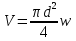
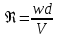
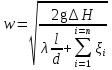 7.Сопоставление (C) w(6п) и w(1п)  если С < 0,1%, то d = d(в первом приближении) если С > 0,1%, то возвращаемся в первый пункт, при этом используем результат первого приближения по скорости; и т.д. Наивыгоднейший диаметр трубопровода. Диапазоны рекомендуемых скоростей. Подход к решению проблемы является общим для многих гидродинамических, тепло- и массообменных процессов. Он базируется на сопоставлении капитальных и эксплуатационных затрат. В основу анализа применительно к трубопроводу используют уравнения расхода и уравнение Дарси-Вейсбаха.  С увеличением диаметра трубопровода возрастают капитальные затраты: пропорционально растет не только диаметр трубы, но и толщина ее стенок. На рисунке изменение капитальных затрат с диаметром описывается кривой К. Но с увеличением диаметра при известных расходах снижается скорость потока, а с ней – энергия, затрачиваемая на преодоление гидравлического сопротивления. Эксплуатационным (энергетическим прежде всего) затратам отвечает кривая Э. Технологов интересует диаметр трубопровода, при котором суммарные затраты (кривая суммы) минимальны. На рисунке минимуму отвечает точка А. Практика показывает, что этому оптимальному диаметру отвечают скорости потоков: для жидкостей – 0,5 – 3,0 м/с; для газов на порядок выше – 5 – 30 м/с. 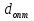   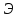 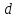 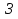 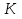 Прямолинейный участок трубопровода, эквивалентный сумме местных сопротивлений трубопровода. Длинный трубопровод. Короткий трубопровод. Короткий трубопровод – это такой трубопровод, потери на местные сопротивления которого соизмеримы с путевыми. Длинный трубопровод – это такой трубопровод, в котором путевые потери много больше местных. Поэтому для длинного трубопровода вводят понятие – длина трубопровода, эквивалентная местным сопротивлениям. 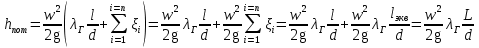 где L есть собственно длина трубопровода плюс длина трубопровода эквивалентная местным сопротивлениям.  Возведем в квадрат левую и правую части уравнения:    Расчет разветвленного трубопровода. Схема разветвленного трубопровода, состоящий из магистрального трубопровода и двух ответвлений, в упрощенном виде.   1 2 3 H1 H0 H3 H2 О  0 0 1 – напорная емкость 2, 3 – приемные емкости; H1/H2/H3 – гидростатический напор в сечениях 1/2/3; точка 0 – узловая точка; H0 – гидростатический напор в узловой точке. Исходное уравнение:  Запишем его для каждого участка: 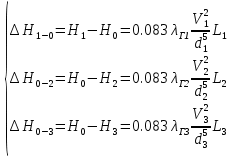 В этой системе из трех уравнений неизвестны четыре величины: d1, d2, d3, H0. Для решения этой задачи четвертым уравнением будет баланс по объемному расходу жидкости: 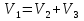 |

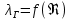 : ламинарный подслой покрывает все выступы. Для таких труб назовем две формулы для нахождения
: ламинарный подслой покрывает все выступы. Для таких труб назовем две формулы для нахождения 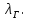
 :в некоторых местах таких труб ламинарная пленка, покрывающая выступы в трубе, рвется наиболее высокими выступами шероховатости, и в таких местах образуются вихри.
:в некоторых местах таких труб ламинарная пленка, покрывающая выступы в трубе, рвется наиболее высокими выступами шероховатости, и в таких местах образуются вихри.