ПГС-Вопросы и ответы. Указание Все ответы должны сопровождаться рисунками Указание 2

• Название: Указание Все ответы должны сопровождаться рисунками Указание 2
• Анкор: ПГС-Вопросы и ответы .doc
• Дата: 24.03.2018
• Размер: 1.18 Mb.
• Имя файла: ПГС-Вопросы и ответы .doc
• Тип: Закон; #17158

Вопросы к экзаменам по технической механике для ПГС в 2012-2013 уч.году

Указание 1. Все ответы должны сопровождаться рисунками

Указание 2. Должны быть даны пояснения обо всех параметрах, входящих в формулы.

Указание 3. На вопросы, обозначенные индексом ***, требуется давать полный ответ

Геометрические характеристики плоских сечений

1. 
   Что называется статическим моментом S_x площади А относительно оси х ? Записать формулу для его вычисления и формулу для вычисления координат центра тяжести фигуры.
   
2. 
   Записать формулу, отражающую зависимость между осевыми моментами инерции относительно параллельных осей, одна из которых центральная
   

РАСТЯЖЕНИЕ-СЖАТИЕ

3. 
   Что такое продольная сила (сила растяжения, внутренняя нормальная сила)? Правило знаков.
   
4. 
   Понятие «напряжение». Закон равномерного распределения нормальногонапряжения σ при центральном растяжении (сжатии) и следствие из него.
   
5. 
   Понятие «линейная деформация». Законы Гука и Дюгамеля-Неймана
   
6. 
   Использование закона Дюгамеля-Неймана о линейном температурном расширении в задаче о стержне, закрепленном с двух концов, при наличии только теплового нагружения. От чего зависят и от чего не зависят температурные и монтажные напряжения? Условие, при котором возникают температурные и монтажные напряжения.
   
7. 
   Метод сечений для вычисления сил растяжения (на примере фермы из двух стержней)
   
8. 
   Закон сохранения энергии и формула Мора для вычисления перемещений точек фермы.
   

Устойчивость сжатых стержней

9. 
   Что значит потеря устойчивости, что такое критическая сила, критическое напряжение, гибкость, коэффициент приведенной длины?
   
10. 
    Формулы Эйлера и Ясинского и области их применения (с пояснениями параметров, входящих в них). Длинные, короткие стержни и стержни средней длины
    
11. 
    ***Вывод формулы Эйлера в случае шарнирного опирания и других видов закрепления.
    

ИЗГИБ БАЛОК

12. 
    Что такое поперечная сила Q_у и изгибающий момент М_х, ?
    
13. 
    Формула Навье для вычисления нормальных напряжений σ при изгибе (с пояснениями параметров, входящих в нее).
    
14. 
    Формула Журавского для вычисления касательного напряжения τ при изгибе (с пояснениями параметров, входящих в нее).
    
15. 
    Виды разрушения балки и условия ее прочности при этом.
    
16. 
    Теорема Шведлера-Журавского (о дифференциальных зависимостях между М_х , Q_у , q).
    
17. 
    ***Доказательство теоремы Шведлера-Журавского и выводы из нее (правила контроля построения эпюр).
    
18. 
    ***Вывод формулы Навье для вычисления нормальных напряжений при изгибе
    
19. 
    Что значит «балка жесткая»? Способы вычисления прогиба балки (записать формулу Мора и дифференциальное уравнение изогнутой оси балки с пояснениями параметров, входящих в них).
    
20. 
    ***Вывод дифференциального уравнения изогнутой оси балки. Доказательство правил Клебша.
    
21. 
    ***Балка на упругом основании: уравнение изогнутой оси балки на упругом основании и выводы из решения о действии на балку сосредоточенной силы.
    

Кручение

22. 
    Что такое крутящий момент? Что значит «вал прочный»? Что значит «вал жесткий»?
    
23. 
    Формулы для вычисления напряжений τ и максимальных напряжений τ_мах для круглого вала, условие прочности.
    
24. 
    Формула для вычисления полного и погонного углов закрутки круглого вала ( с пояснениями параметров, входящих в нее). Условия жесткости вала.
    
25. 
    ***Вывод формулы для вычисления касательного напряжения в стержне круглого сечения
    
26. 
    ***Вывод формулы для вычисления угла закрутки длякруглого вала
    
27. 
    Кручение тонкостенного стержня с замкнутым контуром сечения. Формулы Бредта для вычисления касательного напряжения и угла закрутки ( с пояснениями параметров, входящих в них).
    
28. 
    ***Вывод формулы Бредта для вычисления касательного напряжения
    
29. 
    ***Вывод формулы Бредта для вычисления угла закрутки тонкостенного стержня
    
30. 
    *** Формулы для вычисления касательного напряжения и угла закрутки тонкостенного стержня с открытым контуром сечения. Сравнение напряжений и углов закрутки для стержней с открытым и замкнутым контуром
    

ДИНАМИЧЕСКИЕ ЗАДАЧИ

31. 
    Что такое коэффициент динамичности k_д при ударе? Формула вычисления коэффициента динамичности k_д при заданной скорости и заданной высоте падения груза на вертикальный брус
    
32. 
    *** Вывод формулы вычисления коэффициента динамичности k_д
    
33. 
    Формула вычисления коэффициента динамичности k_д с учетом массы груза и балки. Область применимости коэффициент динамичности.
    
34. 
    Принцип Даламбера. Что такое свободные и вынужденные колебания упругих стержней. Что такое собственная частота колебаний? Явление резонанса
    
35. 
    *** Вывод уравнения и его решение в случае свободных продольных колебаний
    
36. 
    *** Вывод уравнения и его решение в случае вынужденных продольных колебаний
    

Тестовые вопросы

37. 
    Во сколько раз увеличится нагрузка, которую может выдержать проволока при растяжении, если ее радиус увеличить в 2 раза?
    
38. 
    Во сколько раз увеличится нагрузка, которую может выдержать при изгибе балка квадратного сечения, изготовленная из хрупкого материала, если сторону квадрата увеличить в 2 раза?
    
39. 
    Во сколько раз уменьшится нагрузка, которую может выдержать балка при изгибе, если длину увеличить в 2 раза?
    
40. 
    Во сколько раз увеличится сжимающая критическая нагрузка, которую может выдержать длинная упругая балка квадратного сечения, если сторону квадрата увеличить в 2 раза ?
    
41. 
    Как различаются нагрузки, которые могут выдержать балки прямоугольного сечения (b:h=1:2) , если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?
    
42. 
    Как различаются прогибы балок прямоугольного сечения (b:h=1:2) , если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?
    
43. 
    В сколько раз увеличится предельный момент, который может выдержать труба при кручении, если ее радиус увеличить в 2 раза, а толщину оставить прежней?
    
44. 
    В сколько раз увеличится предельный момент, который может выдержать при кручении сплошной вал , изготовленный из хрупкого материала, если ее радиус увеличить в 2 раза?
    
45. 
    В сколько раз уменьшится угол закрутки сплошного вала при кручении, если ее радиус увеличить в 2 раза?
    
46. 
    От чего зависят температурные напряжения: а) от длины стержня, b) от площади сечения, c) от формы сечения,. d) от материала?
    

Примечания.

1). В билете будут 4 вопроса и одна задача

2).Вопросы, отмеченные индексом ***, необходимо знать студентам, желающим получить оценки 4 и 5

Лектор: Зав. кафедрой, профессор Р.А. Каюмов

Вопросы и ответы на вопросы

Геометрические характеристики плоских сечений
1. Что называется статическим моментом S_x площади А относительно оси х ? Записать формулу для его вычисления и формулу для вычисления координат центра тяжести фигуры.

Статическим моментом S_x площади A относительно оси х называется произведение площади на плечо (расстояние до данной оси).



Отсюда вытекает, что


.

2. Записать формулу, отражающую зависимость между осевыми моментами инерции относительно параллельных осей, одна из которых центральная.





РАСТЯЖЕНИЕ-СЖАТИЕ
3. Что такое нормальная сила (продольное усилие)? Правило знаков.

Рассечем брус на две части. Продольной силойNврассматриваемом внутреннем сеченииназывается равнодействующая всех внешних осевых сил, с которой левая часть воздействует на правую часть или наоборот. Если внешняя сила действует на сечение растягивающим образом, то она дает вклад в N со знаком «+», если действует сжимающим образом, то она делает вклад в N со знаком «-». Например, N = F₃ - F₄ или N = F₁+ F₂


4. Понятие «напряжение». Закон равномерного распределения напряжения σ при центральном растяжении (сжатии) и следствие из него.?

Рассечем брус на две части. Рассмотрим воздействие

верхней части бруса на сечение. Она давит

на нижнюю часть поверхностной нагрузкой по нормали

к сечению. Эта нагрузка (давление) называется

нормальным напряжением. Другими словами,

нормальное напряжение это интенсивность

усилия сжатия или растяжения. Если напряжение

действует на сечение растягивающим образом,

то оно считается положительным.
Закон равномерного распределения напряжения σ

при центральном растяжении (сжатии):

σ = const,

поэтому σ = N / A

5. Что такое относительная( линейная) деформация? Правило знаков. Законы Гука и Дюгамеля-Неймана

Рассмотрим брус. В результате деформирования малый элемент получит абсолютное удлинение на величину.

Линейной деформацией называется относительное удлинение, т.е величина
Правило знаков:

если элемент удлиняется, то (т.к. ),

если элемент укорачивается то (т.к. )

Закон Гука: чем больше сила, тем больше деформация, причем, прямо пропорционально силе. При простом растяжении бруса продольной силой этот закон можно записать в виде:. Здесь продольная сила, l - длина элемента, А - площадь его поперечного сечения, Е - модуль Юнга. В компонентах напряжений и деформаций, закон Гука записывают следующим образом: .
закон Дюгамеля – Неймана (закон линейного температурного расширения).
При наличии перепада температур тела изменяют свои размеры, причем, прямо пропорционально этому перепаду температур.
.

Здесь α - коэффициент линейного температурного расширения.


6. Использование законов Гука и Дюгамеля-Неймана в задаче о стержне, закрепленном с двух концов, при наличии только перепада температур.

Из рисунка видно, что: , то есть

.

Отсюда находим температурное напряжение:

Видно, что температурное напряжения не зависит ни от длины стержня, ни от формы сечения, ни от ее площади. Температурное напряжения зависят только от материала, т.е. от Е, α, и от перепада температуры Т .

Аналогично, монтажные напряжения зависят только от материала (т.е. от Е)и от удельной неточности изготовления δ стержня , т.к. получим, что).

Температурные и монтажные напряжения возникают только при наличии лишних связей. Но если нет лишних связей, (то есть задача статически определима), то температурные и монтажные напряжения не возникают.

Например, рассмотрим конструкцию, изготовленную из двух стержней:



Если ее нагреть, то она деформируется. Покажем, что нет напряжений. Сделаем сечение и запишем уравнения равновесия для верхней части:



Получили, что напряжения равны нулю в обоих стержнях.

Аналогично показывается, что и монтажные напряжения не возникают, если нет лишних связей.

7. Метод сечений для вычисления сил растяжения (на примере фермы из двух стержней) .
Рассечем конструкцию на 2 части и запишем условия равновесия правой части:





Отсюда, находим , .


8. Закон сохранения энергии и формула Мора для вычисления перемещений точек фермы

Согласно закону сохранения, никакая работа не исчезает, она тратится на совершение другой работы или переходит в другую энергию. Согласно этому закону формулу Мора можно записать в виде:



- искомое перемещение,

- удлинения стержней, которые появляются под действием внешних рабочих нагрузок:

Задача о действии рабочих нагрузок изображена на рисунке:


- усилия растяжения стержней, которые возникают от действия единичной силы Т , которая приложена в интересующей нас точке и в направлении . Задача о действии единичной силы Т изображена на рисунке:



Устойчивость сжатых стержней
9. Что значит потеря устойчивости, что такое критическая сила, критическое напряжение, гибкость, коэффициент приведенной длины?

Рассмотрим сжатый стержень. При некотором значении Р происходит резкая смена прямолинейной формы в криволинейную при малейшем поперечном воздействии. Это явление называется потерей устойчивости. Сила Ркр, при которой это происходит, называется критической, а соответствующее ей напряжение называют критическим напряжением: . Гибкость - это относительная длина стержня (безразмерная величина): Здесь - коэффициент приведенной длины (вычисляется через число волн, образующихся при изгибе): .

10. Формулы Эйлера и Ясинского и области их применения (с пояснениями параметров, входящих в них).

Формула Эйлера: , где гибкость стержня, Е - модуль Юнга.

Ее нужно применять для тех стержней, у которых после вычислений

получится (для стали это условие обеспечивается, если ).

Такие стержни называются длинными

Формула Ясинского: (а и b - постоянные, зависящие от материала).

Ее нужно применять для тех стержней, у которых после вычислений получится (для стали это условие обеспечивается, если ). Такие стержни называются стержнями средней длины

Короткие стержни – это стержни, которые не теряют устойчивость, для них и по формуле Эйлера, и по формуле Ясинского получится (для стали это условие обеспечивается, если ).

ИЗГИБ БАЛОК
12. Что такое поперечная сила, изгибающий момент?

Рассечем брус на две части. Суммарная сила, с которой левая часть бруса воздействует на правую поперек оси бруса, называется поперечной силой Q_y. Например, в сечении на расстоянии 3 м. Q_y= -2т. (См. рисунок)

Суммарный момент, с которым левая часть бруса воздействует на правую относительно оси, поперечной брусу (относительно оси х), называется изгибающим моментом М_х. Например, в сечении на расстоянии 3 м.

М_х = -2т∙3м.+1т∙м. (См. рисунок)


13. Формула Навье для вычисления нормальных напряжений σ при изгибе ( с пояснениями параметров, входящих в нее).



Здесь Jx - момент инерции, у – расстояние от нейтральной линии 0х до точки в которой вычисляется напряжение



14. Формула Журавского для вычисления касательных τ при изгибе.

, - поперечная сила; - момент инерции всего сечения; b - ширина сечения на уровне точки (микроэлемента), в которой вычисляется ; = Аотс ∙(уц.т.)отсстатический момент отсеченной площади ВСDK ,которая лежит ниже рассматриваемой точки, Аотс – площадь ВСDK (отсеченнойчасти сечения), (уц.т.)отс - координата центра тяжести отсеченной площади ВСDK. Если фигура не прямоугольник, то ширина b будетразная на разных уровнях рассматриваемой точки.

15. Виды разрушения балки и условия ее прочности при этом.
1) Разрушение изломом, соответствующее условие прочности (условие прочности по нормальным напряжениям):

_,



2) Разрушение срезом, соответствующее условие прочности (условие прочности по касательным напряжениям):




3)Разрушение сколом и соответствующие условия прочности:

для хрупких материалов - по первой теории прочности , т.е. по главным напряжениям. для пластичных материалов - условие прочности по четвертой теории прочности

16. Теорема Шведлера-Журавского (дифференциальные зависимости между М_х, Q_у, q) . Следствие из него

, . Следствие: там где эпюра меняет знак, там на эпюре имеет место экстремум.

19. Что значит «балка жесткая»? Способы вычисления прогиба балки (записать формулу Мора и дифференциальное уравнение изогнутой оси балки с пояснениями параметров, входящих в них).

Балка называется жесткой, если для заданных рабочих нагрузок она прогибается в пределах нормы, т.е. , если v <[v]. Формула Мора . Уравнение изогнутой оси балки:

Здесь - искомый прогиб в точке B (от рабочих нагрузок); - изгибающий момент от рабочих нагрузок, Т = 1 – единичная сила, приложенная в интересующей нас точке В в направлении искомого прогиба, - изгибающий момент в фиктивной задаче о приложении к балке силы Т .
Кручение
22. Что такое крутящий момент? Что значит «вал прочный»? Что значит «вал жесткий»?

Суммарный момент, которым левая часть вала воздействует на правую (или наоборот), называется крутящим моментом . Например, в сечении I-I получим Мz = m1 – m2 Вал называется прочным, если не возникнет опасности разрушения вала при заданных нагрузках, т .е. если Вал называется жестким, если он деформируется в пределах нормы при заданных нагрузках, т.е., если полный угол закрутки , и погонный угол закрутки

23. Формулы для вычисления напряжений τ и максимальных напряжений τ_мах для круглого вала, условие прочности.

, Здесь ρ – расстояние от центра сечения до точки, в которой вычисляется напряжение Jp= 2Jx - полярный момент инерции: Условие прочности:

24. Формула для вычисления полного φ и погонного θ углов закрутки круглого вала ( с пояснениями параметров, входящих в нее). Условия жесткости вала.






Здесь J_p= 2J_x - полярный момент инерции,

l – длина вала, G – модуль сдвига
Условия жесткости вала : ,

Если вал состоит из нескольких участков, то полный угол закрутки
27. Кручение тонкостенного стержня с замкнутым контуром сечения. Формулы Бредта для вычисления касательного напряжения и угла закрутки ( с пояснениями параметров, входящих в них).

, где А* - площадь просвета трубы, t– ее толщина. , где - относительный периметр (в случае постоянной толщины:, в случае разных толщин: )

ДИНАМИЧЕСКИЕ ЗАДАЧИ
31. Что такое коэффициент динамичности k_д при ударе? Формула вычисления коэффициента динамичности

Коэффициент динамичности: . Здесь сила, которая равна весу F ударяющего тела и действует статически, . - сила удара ,

Формула вычисления коэффициента динамичности k_д при заданной скорости груза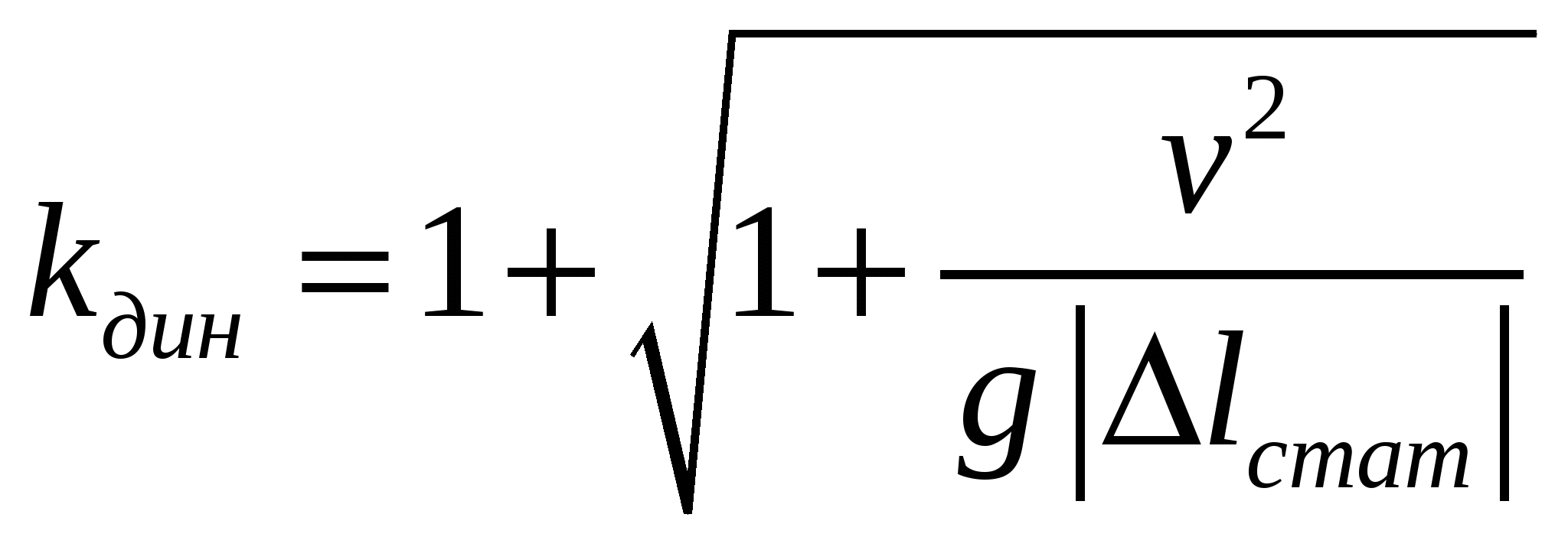



Здесь v- скорость ударяющего тела
33. Формула вычисления коэффициента динамичности k_дин с учетом массы груза и балки. Область применимости коэффициент динамичности

.

Здесь m-масса груза (), -масса стержня, с- поправочный коэффициент, зависящий от способа закрепления и вида удара (продольного или поперечного). Например, при поперечном ударе по шарнирно опертой балке , при продольном ударе .

Область применимости коэффициент динамичности:

34. Принцип Даламбера. Что такое свободные и вынужденные колебания упругих стержней. Что такое собственная частота колебаний? Явление резонанса
Если ускорения элементов конструкции известны, то динамическую задачу можно свести к статической. Для этого надо добавить силы инерции к внешним нагрузкам и решать задачу к обычную статическую.

Свободные колебания – это колебания при отсутствии внешних сил. Собственная частота колебаний ω - это число колебаний конструкции в единицу времени при отсутствии внешних сил.

Вынужденные колебания – это колебания конструкции от воздействия внешних сил.

Если собственная частота колебания конструкции ω будет приближаться по величине к частоте изменения внешней силы ω_о, то амплитуда колебаний становится неограниченно большой, это явление называется резонансом.


Тестовые вопросы
37. Во сколько раз увеличится нагрузка, которую может выдержать проволока, если ее радиус увеличить в 2 раза?



Ответ: в 4 раза, т.к. N=σ∙A= σ∙π∙r²
38. Во сколько раз увеличится нагрузка, которую может выдержать балка квадратичного сечения, изготовленная из хрупкого материала, если сторону квадрата увеличить в 2 раза?



Ответ: в 8 раз, т.к. σ_max=M_x/W_x, M_x =P∙l, W_x= a³/6
39. Во сколько раз уменьшится нагрузка, которую может выдержать балка, если длину увеличить в 2 раза?
Ответ: в 2 раза, т.к. σ_max=M_x/W_x, M_x =P∙l,

40. Во сколько раз увеличится сжимающая критическая нагрузка, которую может выдержать длинная упругая балка квадратного сечения, если сторону квадрата увеличить в 2 раза ?


Ответ: в 16 раза, т.к. Р_кр=∙π²∙J_x/E(μ∙l)², J_x = a⁴/12
41. Как различаются нагрузки, которые могут выдержать балки прямоугольного сечения, изготовленная из хрупкого материала, (b:h=1:2), если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?

.


Ответ: в 2 раза, т.к. σ_max=M_x/W_x, M_x =P∙l,

В первом случаеW_x= bh²/6= 2a³/6, во втором случае W_x= bh²/6= 4a³/6,

42. Как различаются прогибы балок прямоугольного сечения (b:h=1:2) , если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?



Ответ: в 4 раза, т.к. v= ∫∫ M_x/EJ_xdz

В первом случаеJ_x= bh³/12= 2a³/12, во втором случае J_x= 4bh²/12= 8a³/12,
43. В сколько раз увеличится предельный момент, который может выдержать труба при кручении, если ее радиус увеличить в 2 раза, а толщину оставить прежней



Ответ: в 4 раза, т.к. τ =M_z/2At_o , A=∙π∙r²
\

44. В сколько раз увеличится предельный момент, который может выдержать при кручении сплошной вал, изготовленный из хрупкого материала, если ее радиус увеличить в 2 раза?



Ответ: в 8 раз, т.к. τ =M_z/ W_р , W_р = π∙r³/2
45. В сколько раз уменьшится угол закрутки сплошного вала при кручении, если ее радиус увеличить в 2 раза?


Ответ: в 16 раз, т.к. φ =M_z∙l / GJ_р , J_р = π∙r⁴/2
46. От чего не зависят температурные напряжения: а) от длины стержня, b) от площади сечения, c) от формы сечения,. d) от материала?
Ответ: от а), b) , c)

47. От чего зависят максимальные напряжения, возникающие под действием собственного веса, в задаче о сжатии колонны: а) от длины стержня, b) от площади сечения, c) от формы сечения,. d) от материала?
Ответ: от b) , c)
Типовые экзаменационные задачи
Задача №1 . Для изображенного на рисунке стержня

1). Проверить прочность

2). Определить полное удлинение, если

[σ]_раст = 1 кН/см², [σ]_сжат = 1.6 кН/см², Е = 210⁴ кН/см², Р₁ = 11 кН, Р₂ = 4 кН, Р₃ = 22 кН, А = 5 см²



Решение: N₁= -11кН, N₂= - 15кН, N₃=7кН

1)

На первом и третьем участках стержень не прочен.

2)
Задача №2.

П

F

роверить, допускается ли сжатие силой 55 т. колонны высотой 5 м. из двутавров №30. Вид сечения показан на рисунке Использовать коэффициент понижения допустимого напряжения на сжатие, [σ]^сж = 1,6 т/см².

Решение

Найдем гибкость: .








Таким образом, = 10,4 см .

Тогда

По таблице , тогда допустимое напряжение
1.6т/см² 0.64 = 10.2 т/см²

Рабочее напряжение:

<<

Вывод: имеем недогрузку.
Задача № 3 Проверить прочность по нормальным и касательным напряжениям, а также жесткость двутавра №30, если [] = 0,9 т/см², [] = 1,6 т/см², [] = l/150, Е = 2000 т/см².

Решение

	Проверка прочности Строим эпюры Qy,Mx(см. рисунок) Проверяем прочность на излом (по нормальным напряжениям). Проверяем прочность на срез (по касательным напряжениям). Вывод: Балка прочна по нормальным и касательным напряжениям.
		Проверка жесткости 1. Найдем допустимый прогиб: 2. Строим эпюру от единичной силы Т=1 (см. рисунок). 3. Рабочий прогиб vвычисляем по формуле Мора. Итегрируем методом трапеций:

Вывод: Поскольку , то балка жесткая.


Задача №4. Для изображенного на рисунке вала круглого сечения требуется:

1. 
   Построить эпюру крутящих моментов M_кр
   
2. 
   Проверить вал на прочность, если радиус сечения R = 10 см., [τ]=0.9т/см²
   
3. 
   Проверить вал на жесткость по погонному углу закрутки, если G=800т/см² , [θ]=0.00001
   

Решение. 1. Построим эпюры напряжений (см. рисунок)

Проверим прочность

2.
3.
Вывод: вал прочный, но не жесткий