урок в 9 классе. Урок по геометрии в 10 классе (02. 09. 2023) Тема урока Окружность. Решение геометрических задач на вычисление из огэ Цели урока

• Название: Урок по геометрии в 10 классе (02. 09. 2023) Тема урока Окружность. Решение геометрических задач на вычисление из огэ Цели урока
• Дата: 18.01.2023
• Размер: 158.5 Kb.
• Имя файла: урок в 9 классе.doc
• Тип: Урок; #891870

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №15 г.Орска»


Окружность.

Решение геометрических задач

на вычисление

из ОГЭ

Подготовила и провела

учитель математики

Резепкина Ольга Васильевна

2022-2023 учебный год

урок по геометрии в 10 классе (02.09.2023)

Тема урока: « Окружность. Решение геометрических задач на вычисление из ОГЭ »
Цели урока:

• отработка умений решать задачи по планиметрии, предлагаемые в тестах ОГЭ;

• развитие внимания, памяти, логического мышления, интереса к предмету,

математически грамотной речи;

• воспитание трудолюбия, усидчивости, чувства ответственности,

познавательной активности.
Тип урока: .
Оборудование: компьютер, телевизор, раздаточный материал.
Ход урока
I. Организационный момент.
Сегодня у нас с вами урок по решению геометрических задач из ОГЭ, поскольку на экзамене по математике есть модуль «Геометрия».
В качестве эпиграфа нашего урока мы возьмем слова известного математика Пойа:
«Лучше решить одну задачу несколькими способами,

чем несколько задач – одним»
II. Актуализация знаний учащихся.
Задания на экзамене предлагаются каждый год разные. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. В экзаменационной работе есть задание № 19, проверяющее, как ученик ориентируется в теоретическом материале. В каждом варианте в задании №19 предлагается вопросы , и надо из них выбрать либо верные утверждения, либо неверные. Иногда из-за одного пропущенного слова меняется смысл сказанного. Поэтому мы начнём наш урок с проверки знания теории.

Какие из следующих утверждений верны?
1. Через любые три точки на плоскости можно провести окружность.

Неверно.

2. Площадь трапеции равна половине высоты, умноженной на разность

оснований.

Неверно.

3. Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Верно

4. В любой четырехугольник можно вписать окружность.

Неверно.

5. Отношение площадей подобных треугольников равно коэффициенту подобия.

Неверно.

6. Стороны треугольника пропорциональны косинусам противолежащих углов.

Неверно.

7. Отношение стороны треугольника к синусу противолежащего угла равно

диаметру описанной окружности.

Верно.

8. Вписанный угол равен половине градусной меры дуги, на которую он опирается.

Верно.

9. Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Неверно.

10. Угол, вписанный в окружность, равен соответствующему центральному углу,

опирающемуся на ту же дугу.

Неверно.

11. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Верно.

12. Биссектрисы треугольника пересекаются в центре вписанной в него

окружности.

Верно.

III. Решение задач.
Начнем мы с вами с решения задач из первой части экзамена, т.е. с задач, оцениваемых в 1 балл. Вы знаете, что на экзамене при решении этих задач надо только дать правильный ответ, записав его в бланк ответов.


Задача на 1 балл

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.

Решение.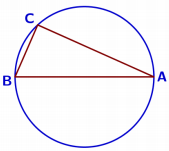


Т. к. точка центр окружности лежит на АВ, то АВ– диаметр окружности . Угол АСВ =90° (прямой). По условию угол BAC равен 24°, отсюда следует что

угол АВС равен 66°,

Ответ: 66° .
Задача на 1 балл

Найдите длину отрезка АN, если радиус изображенной на рисунке окружности ОК =3, АК = 2.
Решение.



1 способ.

АN – касательная к окружности, АМ – секущая. Если из точки А к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки А до точки касания равен произведению отрезков секущей от точки А до точек пересечения секущей с окружностью. АN² = АК ∙ АМ = 2 ∙ 8 = 16 АN = 4.
2 способ

Проведем радиус ОN. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Значит, ∆АNО – прямоугольный. АО = 5, NО = 3. По теореме Пифагора .
Ответ: 4.

Во второй части экзаменационной работы есть задачи на 2 балла.
Задача на 2 балла
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.


Решение.  Угол PBK  — вписанный, он равен 90° и опирается на дугу KHP, следовательно, дуга KHP равна 180°, значит, хорда PK — диаметр окружности и 

 

Ответ: 16.

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.


Решение.  Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда   Аналогично, равны треугольники COK и KOD, откуда   Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:



Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём 



Таким образом, 

 

Ответ: 48.

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.







Рассмотрим четырехугольник PKBC. PKBC вписан в окружность, следовательно выполняется условие: сумма противоположных углов четырехугольника равна 180° (условие того, что четырехугольник можно вписать в окружность). Т.е. ∠PKB+∠BCP=180° ∠PKB+∠AKP=180° (т.к. это смежные углы). Следовательно, ∠AKP=∠BCP Рассмотрим треугольники ABC и AKP. ∠AKP=∠BCP (это мы выяснили чуть выше) ∠A - общий, тогда эти треугольники подобны (по признаку подобия). Следовательно, KP/BC=AK/AC=AP/AB (из определения подобных треугольников). Нас интересует равенство KP/BC=AP/AB KP/BC=18/(1,2BC) KP=18BC/(1,2BC)=15 Ответ: KP=15

На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый.

Найдите угол ABC. Ответ дайте в градусах.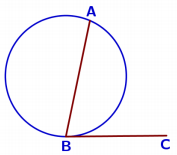


Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.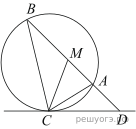


Рассмотрим треугольники ADC и CBD. ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по теореме). ∠CDB - общий для обоих треугольников, следовательно, по признаку подобия, треугольники ADC и CBD - подобны. Следовательно, по определению подобных треугольников запишем: CD/BD=AC/BC=AD/CD По первому свойству биссектрисы: AC/BC=AM/MB=10/18 Так как AC/BC=AD/CD, то AD/CD=10/18 => AD=CD*10/18 Так как CD/BD=AC/BC, то CD/BD=10/18 => BD=CD*18/10 Заметим, что BD=AD+AB=AD+18+10=AD+28 Тогда, подставим AD+28 вместо BD: AD+28=CD*18/10 А теперь вместо AD подставим CD*10/18 (равенство полученное ранее). CD*10/18+28=CD*18/10 28=CD*18/10-CD*10/18 Приводим правую часть к общему знаменателю: 28=(18*18*CD-10*10*CD)/180 28*180=CD(324-100) CD=28*180/224=180/8=22,5 Ответ: 22,5
Домашнее задание.
Пожелания и советы учащимся
• Помни и понимай, что подготовка к ОГЭ – это тяжелый труд, где

результат будет прямо пропорционален времени, потраченному на

активную подготовку к экзамену.
• Выполняй как можно больше различных тестов по предмету.
• Тренируйся с секундомером в руках, засекай время выполнения тестов.

• Готовясь к экзаменам, мысленно рисуй себе картину успеха.


Рефлексия
Подведение итогов
Выставление оценок
Литература
1. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов и др. − М. : Просвещение, 2009.
2. Математика. 9 класс.