Выполнение чертежа, аксонометрической проекции и разверток комбинированного геометрического тела, усеченного проецирующей плоско. Выполнение чертежа, аксонометрической проекции и разверток комби. Выполнение чертежа, аксонометрической проекции и разверток комбинированного геометрического тела, усеченного проецирующей плоскостью
 Скачать 0.49 Mb.
|
|
Практическая работа № 6 «Выполнение чертежа, аксонометрической проекции и разверток комбинированного геометрического тела, усеченного проецирующей плоскостью» Цели занятия: Обучающая: Развить умение строить чертежи, аксонометрические проекции и развертки геометрических тел, рассеченных проецирующими плоскостями Развивающая: продолжить формирование приемов логического мышления (сравнение, анализ, синтез). Воспитательная: воспитывать потребность трудиться и добиваться наилучших результатов в учебе. Тип урока: выработка и закрепление умений и навыков Содержание : Построить в трех проекциях чертеж комбинированного геометрического тела, усеченного проецирующей плоскостью. Выполнить аксонометрическую проекцию и развертку . Оформление: Чертеж выполнить на листах чертежной бумаги А3, обязательно с рамкой и основной надписью. Методические указания В левой части формата расположить оси координат для построения трех проекций фигуры. Справа необходимо оставить место для построения аксонометрического изображения. Решение задачи рекомендуется начинать с построения проекций фигуры. По данным таблицы 1 строятся фронтальная и горизонтальная проекции. При этом рекомендуется горизонтальную проекцию располагать отстоящей от оси координат на 10–15 мм, а фронтальную – по оси Х. За- тем по двум заданным проекциям строится профильная проекция фигуры. Во всех вариантах фигура представляет собой комбинированное те- ло, состоящее из простейших геометрических фигур – призмы и усечен- ного конуса. Призма является правильной, поэтому для построения ее ос- нования задан диаметр описанной окружности. Решение задачи рекомендуется начинать с анализа чертежа. Сквозное призматическое отверстие представляет собой набор фронтально-проецирующих плоскостей, которые в пересечении с призмой и конусом дают определенные линии пересечения. Сначала необходимо определить вид линии пересечения, который зависит от взаимного расположения геометрического тела и плоскости. Пример 1. Пересечение призмы фронтально-проецирующей плоскостью. В сечении призмы фронтально-проецирующей плоскостью получается плоский многоугольник, вершины которого строят как точки пересечения ребер призмы с секущей плоскостью (рис. 1). При этом на фронтальной плоскости проекции проекция многоугольника – отрезок, совпадающий в прямой – проекцией проецирующей плоскости.  Рисунок 1- Пересечение призмы с проецирующей плоскостью 19 Пример 2. Пересечение конической поверхности плоскостью. В зависимости от взаимного расположения конической поверхности вращения и плоскости получаются различные линии пересечения: пря- мые, окружность, эллипс, парабола, гипербола и даже точка. Вид указан- ных линий определяется положением секущей плоскости относительно вершины конической поверхности и соотношением между величинами углов наклона секущей плоскости и наклона образующей конической по- верхности к ее оси. На рисунке 2 показаны примеры пересечения конуса плоскостями различного положения. Изображения представлены фронтальными про- екциями конуса и его оси вращения. Угол γ – угол наклона плоскости к оси вращения конуса. Если прямой круговой конус пересекает плоскость, параллельную основанию, т.е. γ = 90 , то линия пересечения боковой поверхности кону- са с плоскостью Qбудет окружностью (рис. 2, а). Если конус пересекается с наклонной плоскостью так, чтобы пере- секались все его образующие, и угол γ ≠ 90 , то линия пересечения боко- вой поверхности конуса с плоскостью Q – эллипс (рис. 2, б). Если секущая плоскость Р проходит через вершину конуса, то плоскость может быть перпендикулярна или наклонна к основанию, т.е. 0 ≤ γ < β. В этом случае линия пересечения боковой поверхности конуса с плоскостью – две пересекающиеся прямые (рис. 2, в). Необходимо заметить, что если γ = β, то секущая плоскость будет касаться конической поверхности по прямой линии. Если секущая плоскость Т параллельна оси конуса, то линией пересечения является гипербола (рис. 2, г). Если плоскость расположена параллельно одной образующей конуса, т.е. γ = β, то боковая поверхность конуса пересекается с этой плоскостью по параболе (рис. 2, д). Например, для построения линии пересечения конуса фронтально- проецирующей плоскостью Q сначала необходимо определить вид линии пересечения. Секущая плоскость Q является наклонной и пересекает все боковые образующие конуса, т.е. γ > β, следовательно, в пересечении получится эллипс (рис. 2, б).  а) окружность б) эллипс в) две прямые  Рисунок 2-Возможные случаи пересечения конуса вращения с проецирующей плоскостью Так как заданная плоскость является фронтально-проецирующей, то на плоскость проекций П2 она проецируется в виде прямой линии, а значит, и искомая линия пересечения (эллипс) спроецируется в отрезок, так как лежит в плоскости Q (рис. 3). Точки А2 и В2 – это точки пересечения секущей плоскости с крайними образующими конуса. Отрезок А2В2 проецируется на фронтальную плоскость в натуральную величину и является большой осью эллипса. Проекции А1 и В1 опорных точек А и В лежат на горизонтальных проекциях левой и правой образующих конуса. На передней и задней образующей конуса расположены опорные точки С и С', фронтальные проекции которых совпадают. Профильные проекции точек С и С' располагаются на профильных проекциях соответствующих образующих. Для построения горизонтальных проекций С'1 и С1 необходимо измерить расстояния  вдоль оси OY (от оси конуса до проекций точек) на профильной плоскости проекций и отложить их на горизонтальной плоскости проекции (от оси конуса до проекций точек). Дальнейшие построения сводятся к нахождению проекций вспомогательных точек линии пересечения. Выбрав произвольную точку М(М2) на фронтальной проекции эллипса, необходимо воспользоваться вспомогательной линией – параллелью (окружностью, принадлежащей боковой поверхности конуса). Рисунок 3- Линия пересечения конуса вращения с плоскостью – эллипс Фронтальная проекция параллели – горизонтальная прямая, проходящая через М2. На горизонтальной плоскости проекций параллель проецируется в натуральной величине в виде окружности, радиус которой равен расстоянию от оси конуса до крайней точки параллели 12. Проекции М1и М'1 определяются по линиям связи на проекции окружности. Построив необходимое количество вспомогательных точек и соединяя их в логической последовательности, получим проекции эллипса. Видимость линий пересечения определяется по опорным точкам методом конкурирующих точек. В случае пересечения конуса плоскостью, параллельной оси вращения конуса, линией пересечения плоскости с боковой поверхностью будет гипербола, так как γ = 0 (рис. 2, г). 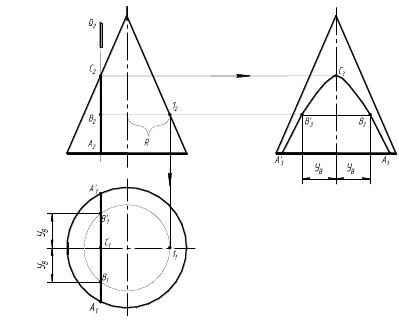 Рисунок 4.-Линия пересечения конуса вращения с плоскостью – гипербола Вершина гиперболы (точка С) получается в результате пересечения секущей плоскости Q с крайней очерковой образующей конуса. На фронтальной плоскости – это точка С2. Горизонтальная и профильная проекции строятся по линиям связи на проекциях соответствующих образующих. Точки А и А' – опорные точки (завершающие точки ветвей гиперболы), проекции которых определяются как точки, принадлежащие основанию конуса. Промежуточная точка В находится с помощью параллели (рис. 4). На рисунке 5 показано пересечение конуса плоскостью, параллельной одной из образующих конуса. Это случай, когда γ = β (рис. 2, д). В результате пересечения получается парабола. Вершина параболы (точка С) получилась в результате пересечения секущей плоскости Q с крайней очерковой образующей конуса. Точки А и А' – опорные точки, проекции которых определяются как точки, лежащие на основании конуса. На передней и задней образующей конуса расположены опорные точки В и В', фронтальные проекции которых совпадают. Профильные проекции точек В и В' располагаются на профильных проекциях соответствующих образующих. Горизонтальные проекции находим по соответствующим расстояниям. Промежуточная точка М находится с помощью параллели.  Рисунок 5- Линия пересечения конуса вращения с плоскостью – парабола Для выполнения данного комплексного задания в левой части формата по заданным размерам вычертить исходные данные (табл. 1). Прежде чем достраивать горизонтальную проекцию и строить профильную, необходимо провести анализ и выполнить дополнительные построения. Этапы выполнения задания представлены на рисунках 6 и 7.  а) проекции призмы б) проекции призмы и усеченного конуса 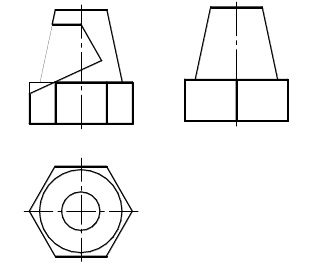 в) проекции комбинированного тела и фронтальная проекция призматического отверстия Рисунок 6-Этапы построения исходных данных задания  а) линия пересечения призмы с плоскостью  б) линия пересечения конуса с плоскостью Рисунок 7- Этапы построения проекций призматического отверстия На рисунке 7, б показано построение линии пересечения конуса с фронтально-проецирующей плоскостью Q. Построения пересечения с плоскостями Т и Р выполняются аналогично. В правой части формата выполняется построение изометрической проекции построенной фигуры. В изометрии все коэффициенты искажения по осям координат равны между собой. Они, при масштабе 1,22:1, равны единице. Рекомендуется ось z аксонометрической проекции совместить с осью фигуры, разместив начало координат в центре нижнего основания. Построение каждой точки фигуры осуществляется по трем ее координатам (х, у, z), определяемым по комплексному чертежу. В практике наиболее распространен способ построения аксонометрической проекции точки по ее вторичной проекции. Окружности основания поверхностей вращения отображаются в аксонометрии в виде эллипсов, которые можно построить по восьми точкам: четыре из которых – это точки окружности, расположенные на осях х и у, а четыре другие – определяются с помощью большой и малой оси эллипсов. При графическом оформлении задания сохраняются все построения. Опорные точки следует обозначить. В аксонометрии линии невидимого контура можно не показывать. Таблица 1 Исходные данные задания «Комбинированное геометрическое тело»   Развертка поверхности Если поверхность, представляемую в виде тонкой, гибкой и нерастяжимой пленки, можно путем изгибания совместить с плоскостью без разрывов и складок, то поверхность, обладающая этим свойством, называется развертывающейся, а фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой. Для развертывающихся линейчатых поверхностей строятся графически приближенные развертки, поскольку в процессе построения развертки эти поверхности заменяются (аппроксимируются) вписанными или описанными многогранными поверхностями. Точные развертки аппроксимирующих многогранных поверхностей принимаются за приближенные развертки развертывающихся поверхностей. Что касается развертки гранной поверхности, то это плоская фигура,составленная из последовательно расположеных плоских многоугольников, конгруэнтных (равных) соответственно ее граням. Поэтому построение развертки гранной поверхности сводится к определению натуральной величины каждой грани. Для этого любым способом преобразования комплексного чертежа на основном чертеже в тонких линиях определяются натуральные величины каждого ребра аппроксимированной гранной поверхности, а затем последовательно способом треугольников строится каждая ее грань. На развертке на образах ребер и граней гранной поверхности построить образы точек линии пересечения поверхностей (рис. 8). Развертку поверхности вращения можно построить, аппроксимировав их гранной поверхностью, т.е. вписав в цилиндрическую поверхность n–угольную призматическую поверхность, а в коническую – n-угольную пирамидальную поверхность, где n – число сторон многоугольника основания. Построение приближенных разверток выполняется в следующей последовательности: 1) заданная развертывающаяся линейчатая поверхность заменяется (аппроксимируется) гранной поверхностью; 2) строится точная развертка гранной поверхности; 3) точная развертка принимается за приближенную развертку заданной поверхности. Но для некоторых линейчатых развертывающихся поверхностей нет необходимости в их замене гранными поверхностями. Так, например, цилиндр вращения радиуса r и высотой h имеет разверткой прямоугольник со сторонами h и  (рис. 9). Разверткой конической поверхности вращения высотой h и основанием радиуса r является сектор радиуса R =  c углом  (ри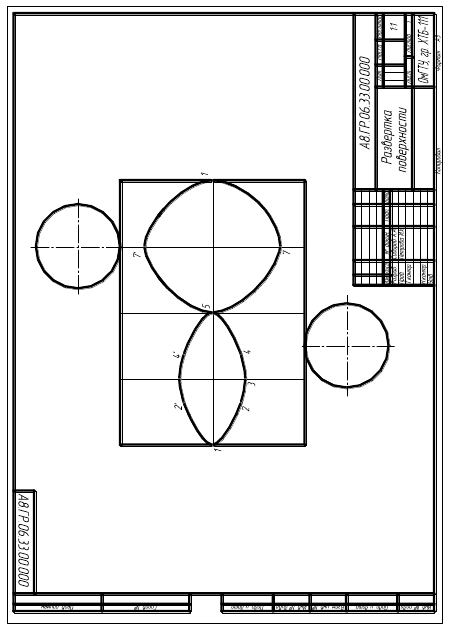с. 10).  Рисунок 8  Рисунок 9  Рисунок 10 К онтрольные вопросы 1. Что называется поверхностью? 2. Как классифицируются поверхности? 3. Что включает в себя определитель поверхности? 4. Как на комплексном чертеже изображаются поверхности? 8. Как может быть расположена плоскость относительно плоскостей проекции? 9. Как образуются коническая и цилиндрическая поверхности? 10. Как образуются гранные поверхности? 11.Как выполняется развертка гранных поверхностей? 12. Как выполняется развертка тел вращения? 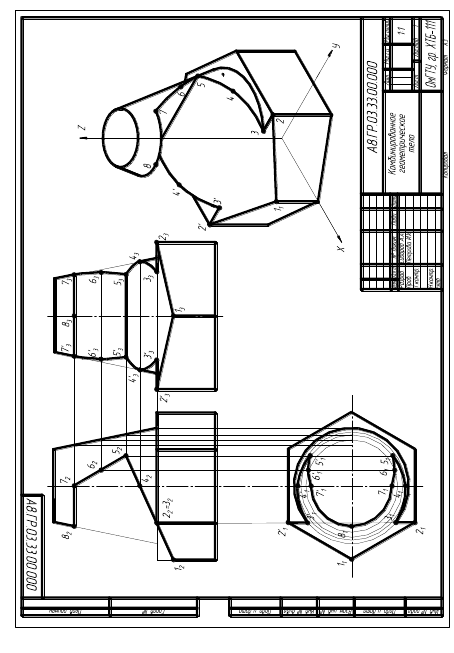 Образец выполнения практической работы №6 |