Вопрос 3 Методы проецирования геометрических фигур. Центральное проецирование
 Скачать 1.78 Mb. Скачать 1.78 Mb.
|
 Вопрос №3 Вопрос №3Методы проецирования геометрических фигур.
П S A A′ B′ B Аппарат: П – плоскость проекции А – точка пространства (А∉ П) А′ - проекция точки А на пл.П S – центр проекции(S∉ П) SA – проецирующая прямая Пересечение проецирующей прямой с плоскостью проекции даст нам проекцию точки. Положение П и центра S определяют аппарат центрального проецирования. Если он задан, то всегда можно определить положение центральной проекции любой точки пространства на плоскости проекции.
Это частный случай центрального пр., центр S удален в бесконечность. Аппарат полностью определяется положением плоскости проекций П и направлением проецирования S. S А В П С′=А′ В′ С Каждой точке пространства соответствует только одна ее проекция на одной плоскости. Обратное утверждение несправедливо (т.е. одной проекции может соответствовать несколько точек, лежащих на одной проецирующей прямой)
Это частный случай параллельного пр., при котором направление проецирования S перпендикулярно плоскости проекции. А В П А′ В′ S 4. Перечислите инвариантные свойства параллельного проецирования. 1) Проекцией точки есть точка.  2) Проекцией прямой есть прямая. 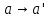 3) Если точка принадлежит прямой, то ее проекция будет принадлежат проекции прямой. 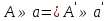 4) Проекция точки пересечения прямых есть точка пересечения проекций этих прямых.  5) Проекции параллельных прямых параллельны.  6) Если плоская фигура ⊥ плоскости проекции, то ее проекция вырождается в линию. 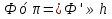 7) Если плоская фигура параллельна плоскости проекции, то она проецируется без искажений.  8) Соотношения длин параллельных прямых равно соотношению длин проекций этих прямых  9)  5. Дайте определение «Прямая частного положения». Классификация. Прямая частного положения, т. е. пряма, расположенная определенным образом относительно плоскостей проекций: параллельно, перпендикулярно плоскостям проекций. Горизонтальная прямая - параллельна горизонтальной плоскости проекций π1. Горизонтально проецирующая прямая  Фронтальная прямая - параллельна фронтальной плоскости проекций π2. Фронтально проецирующая прямая  Профильная прямая - параллельная профильной плоскости проекций π3. Профильная проецирующая прямая  Горизонталь - линия в плоскости параллельная  Фронталь – линия в плоскости параллельная  6. Дайте определение «Плоскость частного положения». Классификация. Плоскостью частного положения называется плоскость параллельная или перпендикулярная одной из плоскостей проекций. Горизонтально проецирующая  Фронтально проецирующая  Профильно проецирующая  Горизонтальная плоскость уровня  Фронтальная плоскость уровня 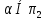 Профильная плоскость уровня  7. Дайте определение термину «След прямой». Опишите алгоритм определения следов прямой общего положения на эпюре. Отобразите в графической форме.
4.  | |    // Эпюр - чертеж, составленный из двух или трех связанных между собой ортогональных проекций геометрической фигуры. 8. Сформулируйте правило определения действительной величины отрезка прямой общего положения по его ортогональным проекциям. Отобразите в графической форме. Для нахождения натуральной величины отрезка требуется построить треугольник, одним катетом которого является горизонтальная(фронтальная) проекция отрезка, а другим разность координат  , гипотенуза в построенном треугольнике будет равна его натуральной величине. , гипотенуза в построенном треугольнике будет равна его натуральной величине.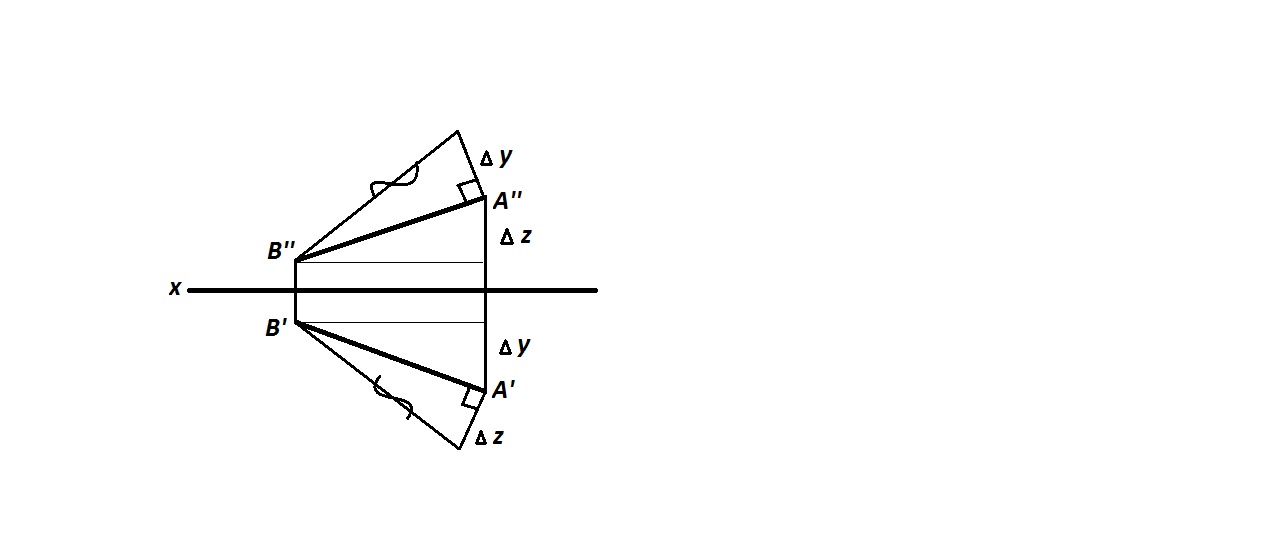 // Ортогональное(прямоугольное) проецирование – частный случай параллельного проецирования перпендикулярно плоскости проекции. 9. Сформулируйте теорему о частном случае проецирования плоского прямого угла. Отобразите в графической форме. Т. Если одна из сторон прямого угла параллельна плоскости проекций, а вторая не перпендикулярна плоскости проекций, то прямой угол проецируется без искажения.  9. Если одна из сторон прямого угла параллельна плоскости проекции, а вторая не перпендикулярна плоскости проекции, то прямой угол проецируется без искажения.  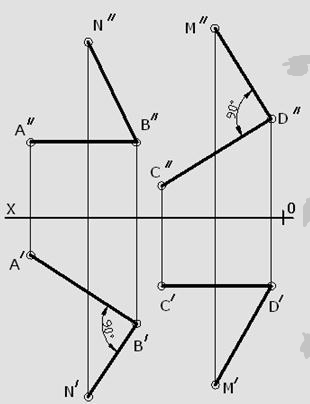 10. Перечислите и опишите способы задания плоскости на эпюре. Отобразите в графической форме. 1. проекциями трех точек не лежащих на одной прямой  2. проекциями прямой и точки вне этой прямой  3. проекциями двух параллельных прямых  4. проекциями двух пересекающимися прямых 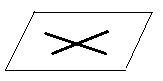 11. Перечислите и опишите особые (главные) линии плоскости. Отобразите в графической форме. 1. Горизонталь – прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекции (h) 2. Фронталь – прямая, лежащая в плоскости и параллельная фронтальной плоскости проекции (f) 3. Профильная – прямая, лежащая в плоскости и параллельная профильной плоскости проекции. 4. Линии наибольшего ската – прямые, проведенные на плоскости перпендикулярно к горизонталям (p) 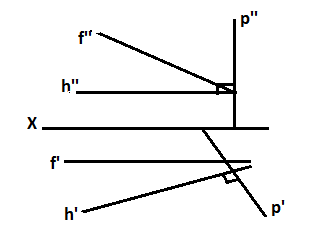
***** 12.Приведите варианты взаимного положения прямой и плоскости. Отобразите в графической форме. 1. прямая параллельна плоскости, если она параллельна хотя бы одной прямой, лежащей в этой плоскости  a|| b a|| α 2. прямая перпендикулярна плоскость, если она перпендикулярна двум пересекающимся прямым этой плоскости  a ┴ m, n a┴ α 3. прямая пересекает плоскость, если прямая не лежит в плоскости и не параллельна ей  a ∩ α = A 4. прямая принадлежит плоскости, если 2 точки прямой принадлежат плоскости 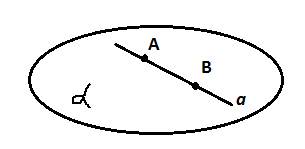 А и В ɛ α а c α А и В ɛ α а c α13 Взаимное положение плоскостей Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться. 1.Пересечение плоскостей. Линия пересечения двух плоскостей –прямая. Положение прямой в пространстве определяют две точки. Чтобы найти линию пересечения плоскостей, достаточно знать две точки, принадлежащие двум плоскостям одновременно.  На рисунке показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника АВС. Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция М2N2совпадает c фронтальным следом P . Горизонтальная проекция искомой линии пройдет через точки М1 и N1, расположенные на горизонтальных проекциях АВ и АС соответствующих сторон треугольника. 2. Плоскости параллельны  Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости. Изображенные на рисунке плоскости Р(n ∩ m)и Т(f ∩ d)параллельны, т.к. n ||f (n2||f2; n1 ||f1)и m ||d (m2||d2; m1 ||d1). ****1) Плоскости перпендикулярны (Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны). *** 14 Классификация поверхностей деталей машин и механизиов 1.Нелинейчатые (Криволинейные): а) Образующая переменного вида: Общего вида 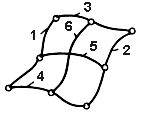 б) Образующая постоянного вида: Трубчатая. 2.Линейчатые (Прямолинейные): а) С тремя направляющими: Косой цилиндр б) С двумя направляющими: Цилиндроид в) С одной направляющей: Цилиндрическая 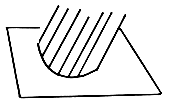 3.Паралельного переноса. 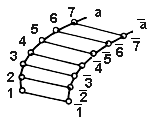 4.Вращения. 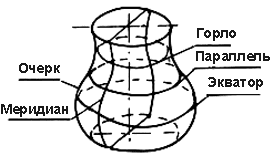 5.Винтовые  15.Дайте определение термину «Поверхность вращения». Особые линии этой пов-ти. Поверхность вращения – эти поверхности образуются вращением образующей(произвольной кривой)  вокруг какой-либо оси (i). вокруг какой-либо оси (i).Кривые плоскость которых проходит через ось (i) называются- меридианы. Каждая точка образующей вращается вокруг неподвижной оси и описывает окружность называется параллель. Параллель с максимальным радиусом называется экватор, с минимальным – горло. Особые линии:
Частные виды: Тор, Сфера, Глоболоид, Эллипсоид вращения, Парабалоид вращения, Гиперболоид вращения, Коническая и цилиндрическая поверхности вращения. Поверхность вращения- поверхность образуемая при вращении образующей вокруг неподвижной оси. Особые линии поверхности вращения: Образующая может быть кривой или прямой линией. Каждая точка образующей вращается вокруг неподвижной оси и описывает окружность, которая называется параллелью. Параллель с максимальным радиусом называется экватор. Параллель с минимальным радиусом называется горло. Кривые линии плоскости, которые проходят через ось называются меридианами.  16. Опишите алгоритм замены плоскостей проекций при преобразовании ортогональных проекций. Перечислите основные позиционные и метрические задачи, решаемые этим способом. Вводится новая плоскость проекция, перпендикулярная уже существующей. Направление поворота новой плоскости относительно точки не имеет значения. Отмеряем координаты точек из тех плоскостей, в которых мы не проводили замену плоскостей и отмеряем их на новой плоскости. (Отрезок переводим в положение линии уровня) 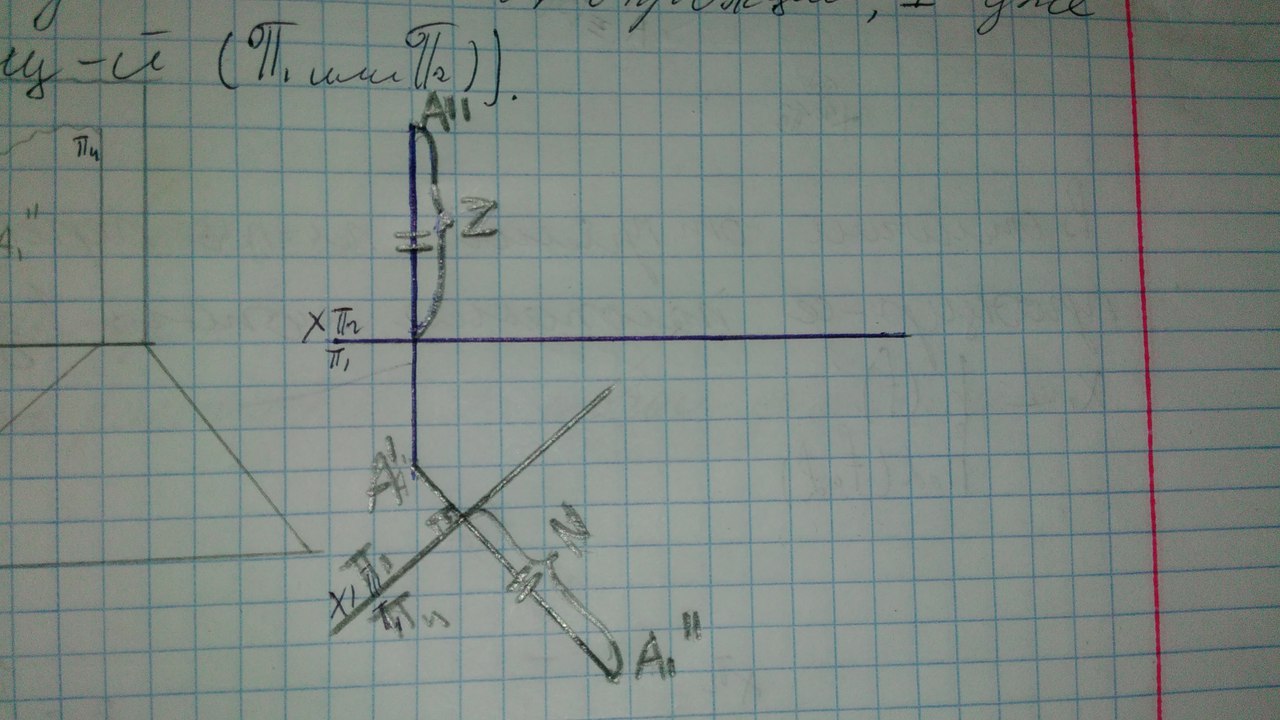 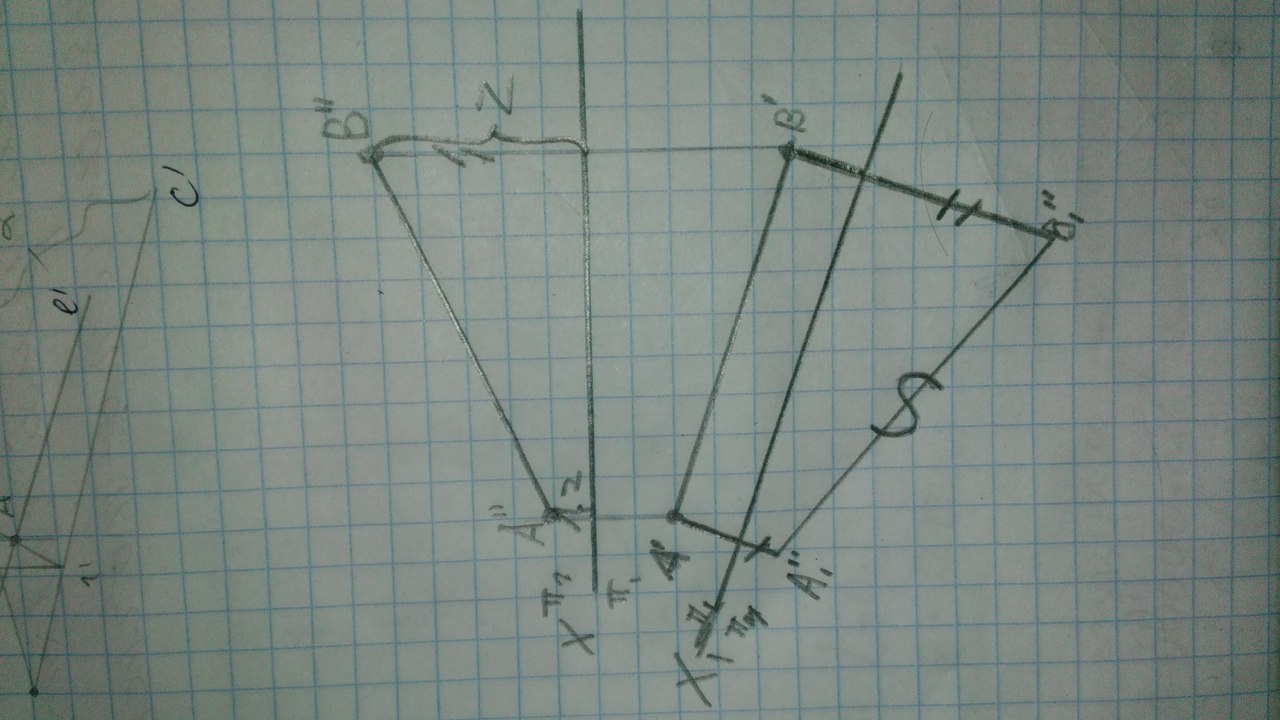 Для того чтобы перевести прямую в проецирующее положение выполняется 2 замены последовательно. 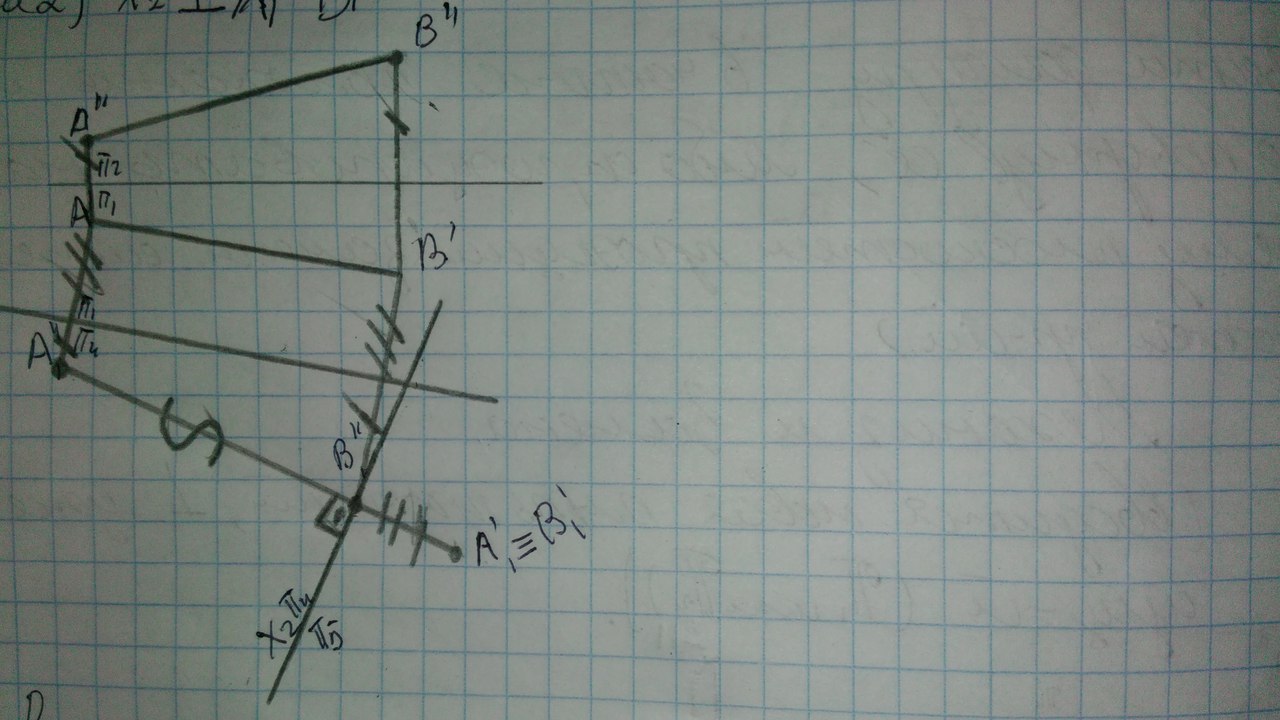 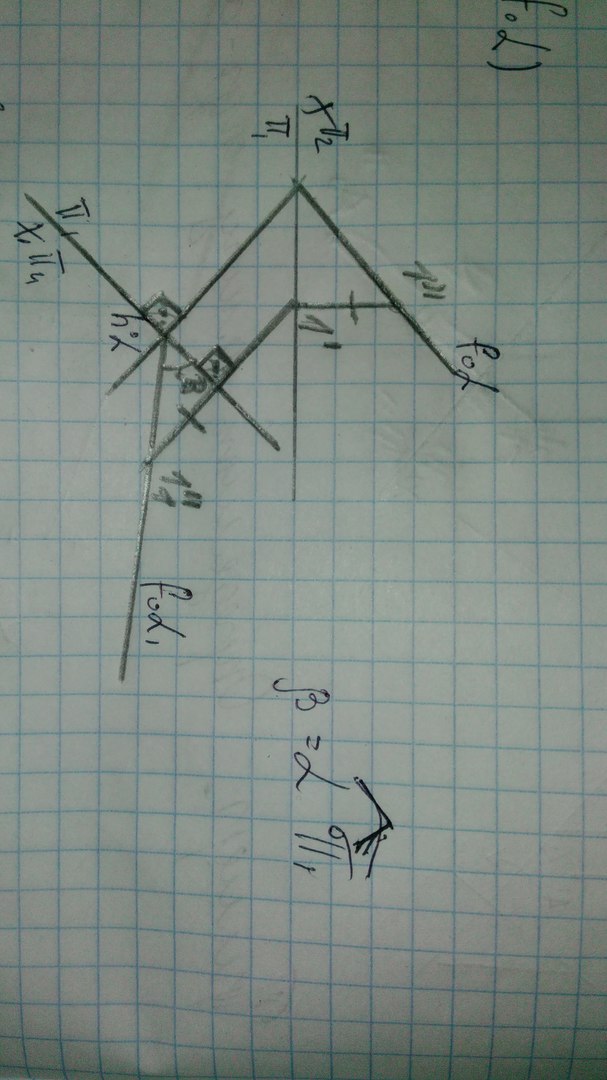 Чтобы плоскость перевести в проецирующее положение нужно сделать 1замену. Новая ось перпендикулярна плоскости. Чтобы перевести плоскость в положение линии уровня делается 2 замены последовательно. Замена 1: Новая плоскость(Х1) перпендикулярна фронтали(горизонтали) Замена 2: Новая плоскость (Х2) параллельна новой проэкции фигуры 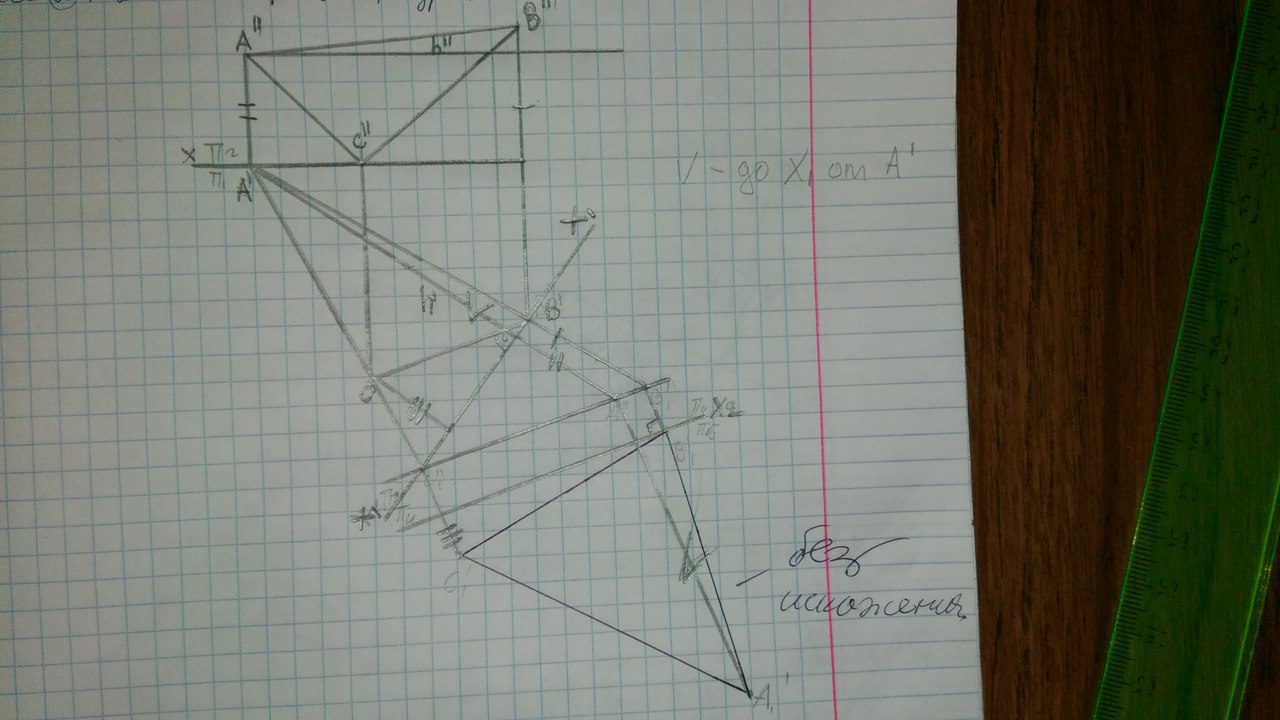 Путем преобразования проекций возможно решение следующих задач:
17. Опишите алгоритм вращения геометрических фигур вокруг оси, параллельной плоскости проекций, при преобразовании ортогональных проекций. Перечислите основные позиционные и метрические задачи, решаемые этим способом. При вращении вокруг горизонтали полская фигура после поворота займет горизонтальное положение, т.е. она будет выглядть в натуральную величину на горизонтальной проекции. Примеры:
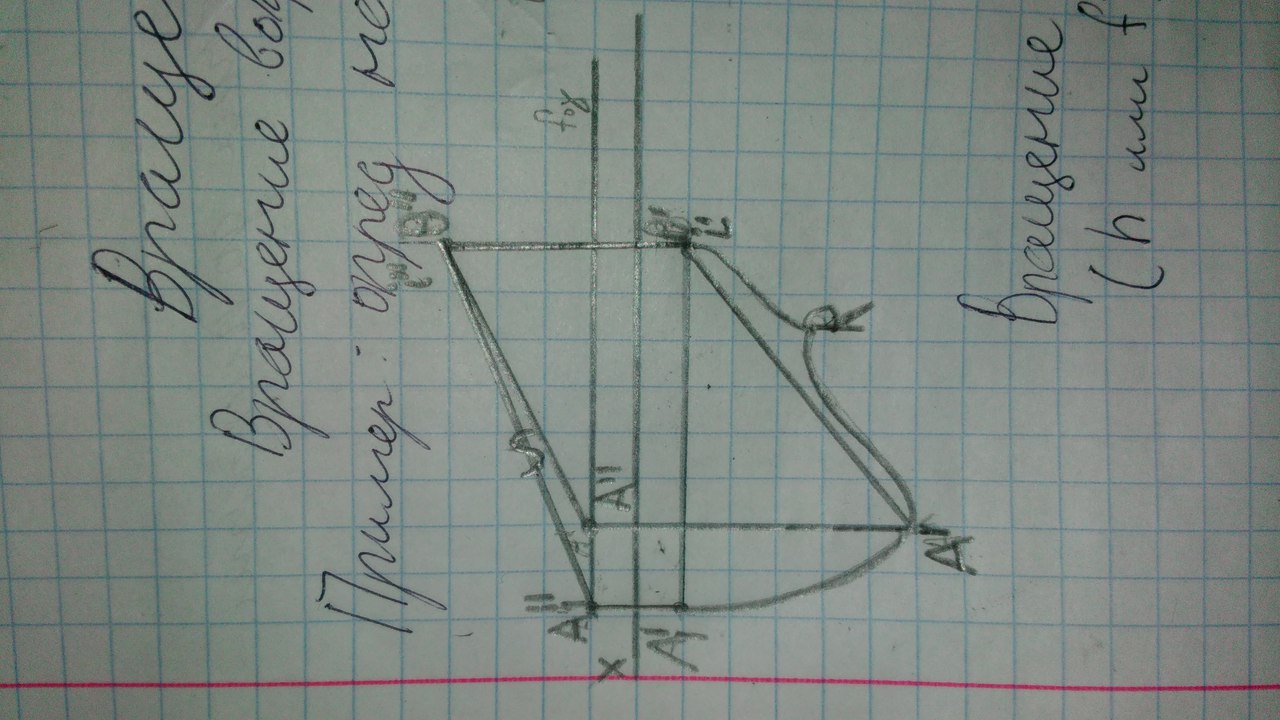
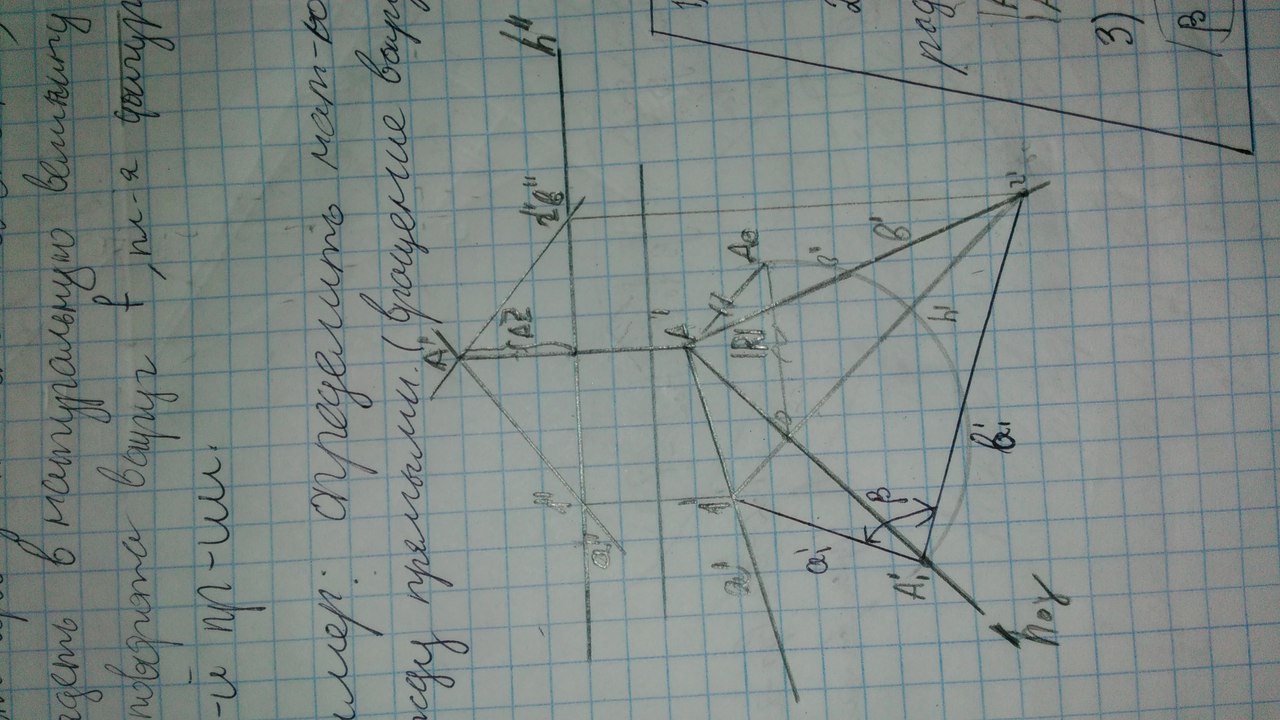 Алгоритм:  Алгоритм:
Шоб все поняли напишу алгоритм от себя: Проводим горизонталь, отмечаем точки 1 и 2 в пересечении прямых и горизонтали. Проецируем точки на горизонтальную плоскость. Соединяем эти точки и проводим перпендикулярно наше новой линии из точки А’ новую линию – плоскость вращения. И перпендикулярно этой плоскости вращения из точки А проводим разность координат (дельта Z которая) и соединяем с точкой О. и из точки О до Ao делаем кружок до нашей проецирующей плоскости. На ней ставим нашу новую точку А и соединяем с точками 1’ 2’ и угол между и есть натуральная величина угла.
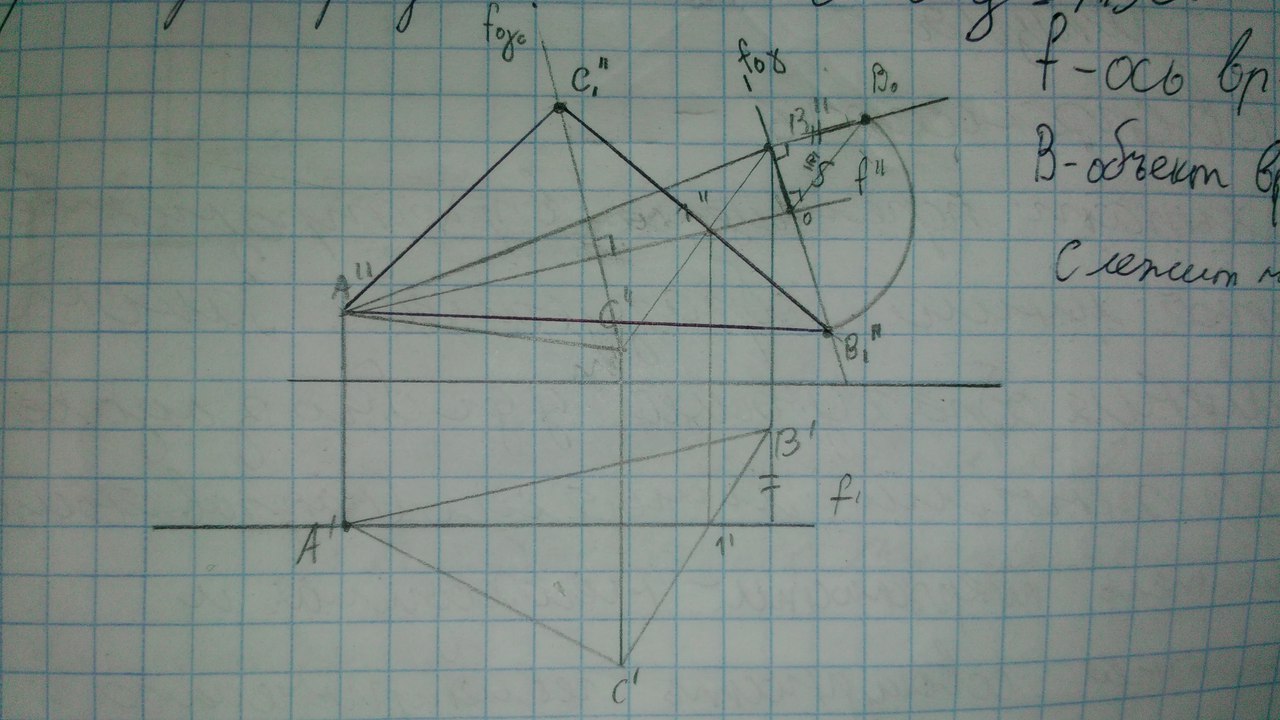 f- ось вращения B – точка вращения. Алгоритм: Проводим фронталь, проецируем точку 1’ на фронтальную плоскость, Из точки А проводим прямую через 1’’ и проводим плоскость вращения перпендикулярно этой нашей новой линии(фронтали). В точке пересечения фронтали и плоскости вращения точка О – центр вращения. От точки В’ отмеряем разность координат до фронтали и перпендикулярно плоскости вращения отмеряем из точки В’’. Проводим линию из точки О до Во и затем проводим циркулем до проецирующей плоскости из точки Во точку В1’’. Так как А лежит на оси вращения, то она не вращалась и сразу соединяем точку А’’ и нашу В1’’. Потом из Точки С’’ перпендикулярно фронтали проводим линию. И из точки В1’’ через точку 1’’ проводим линию. На пересечении этих 2х линий будет точка С1’’. Вот и всё. 18. Опишите алгоритм определения линии пересечения поверхностей на эпюре в общем случае. Приведите классификацию способов определения линии пересечения поверхностей. Алгоритм:
Классификация:
(ПРИМЕРОВ У МЕНЯ НЕТУ) 22 вопрос Две пересекающиеся поверхности касаются третьей поверхности второго порядка. Теорема (теорема Г.Монжа). Если две поверхности второго порядка описаны около третьей поверхности (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка (эллипс, окружность, гиперболу, параболу). Причем, плоскости этих кривых проходят через прямую, соединяющую точки пересечения линии касания. Если две пересекающиеся поверхности второго порядка могут быть описаны вокруг третьей поверхности второго порядка или вписаны в нее, то они пересекаются по двум плоским кривым второго порядка. Теорема Монжа — частный случай теоремы о двойном соприкосновении. ПРИМЕНЕНИЕ: Как видим, обе рассматриваемые поверхности описаны вокруг сферы. Построим решение сначала на П2. Очевидно, точки 12, 22, 32, 42являются точками пересечения конуса и цилиндра, так как лежат на контурных образующих. Тогда в соответствии с теоремой Монжа решением являются две прямые, проходящие через точки 12и 32и точки 22и 42, так как эти прямые представляют собой фронтальные проекции плоскостей, упомянутых в теореме. В данном случае полученные линии пересечения цилиндра и конуса являются эллипсами, построение которых на П1ничем не отличается от построения любой линии, лежащей на поверхности конуса. Выбирая точки на фронтальной проекции каждой из линий 13 и 24, получаем их горизонтальные проекции. Точки 1, 2, 3, 4 лежат на образующей конуса, параллельной П2, поэтому их положение наП1можно найти по линии связи, проходящей через 12, 22, 32, 42. Точки 5 и 6 выбраны на образующей цилиндра, также параллельнойП2, что позволяет по фронтальным проекциям 52и 62найти горизонтальные проекции 51и 61соответственно, которые являются точками перехода видимой части горизонтальной проекции линий пересечения цилиндра и конуса в невидимую. Точка 7 является точкой касания цилиндра и конуса. Ввиду симметрии относительно фронтальной плоскости уровня решение на П1симметрично относительно горизонтальной оси, а наП2видимые участки линии пересечения совпадают с невидимыми. 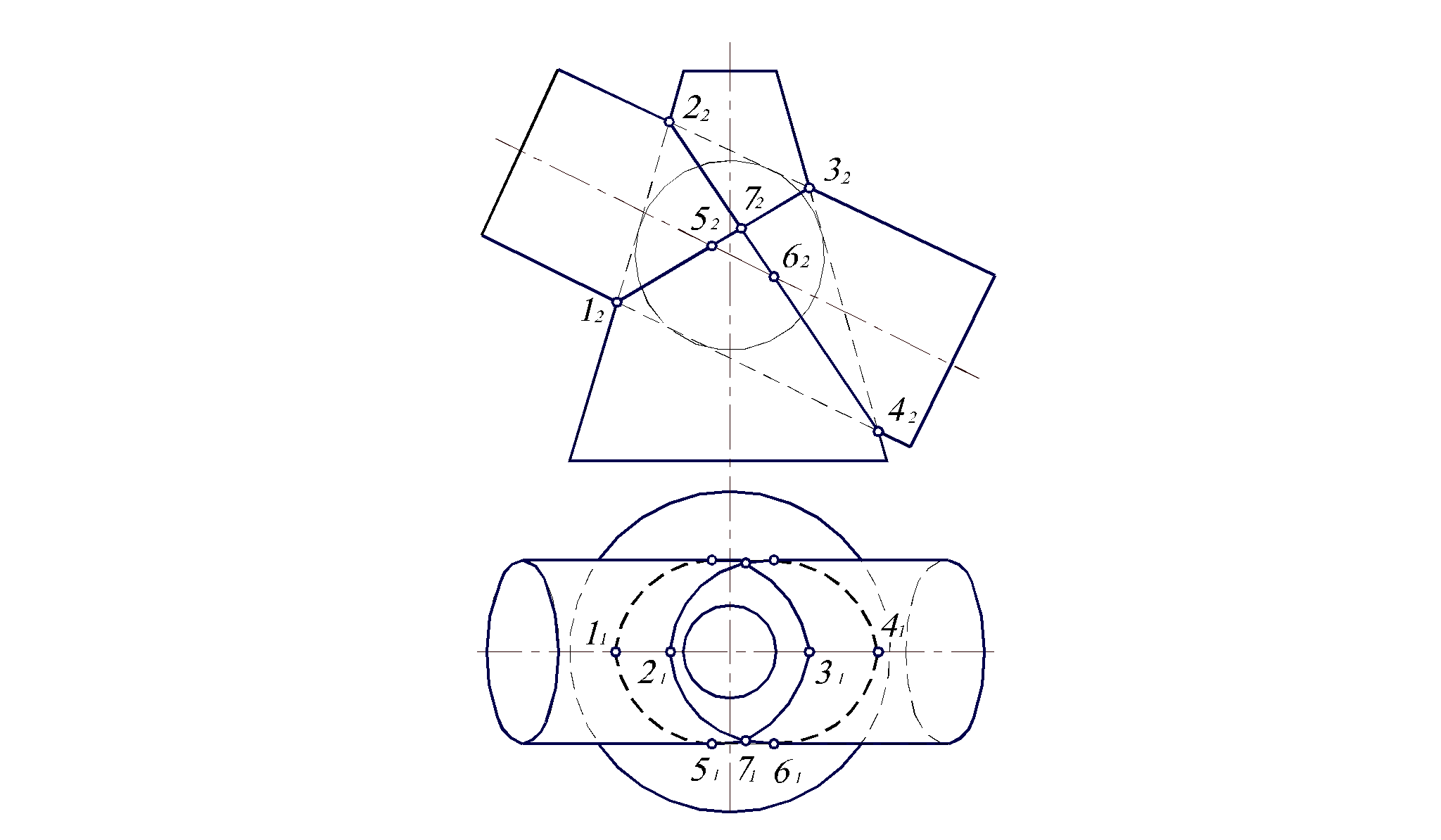 23. Опишите алгоритм определения углов наклона прямой общего положения к горизонтальной и фронтальной плоскостям проекций на эпюре. Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника. Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня. Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций . 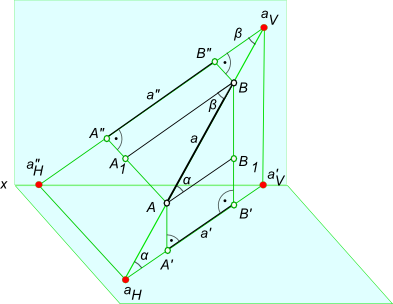 tg α= BB1/AB1=(BB`−B`B1)/AB1=(zB−zA)/A`B` ****** Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
******* 24. опишите алгоритм определения углов наклона плоскости общего положения к горизонтально и фронтальной плоскостям проекции на эпюре. Отобразите в графической форме. Алгоритм:
h2 ║x; h2→ h1 
C1 21┴h1 21→ 22 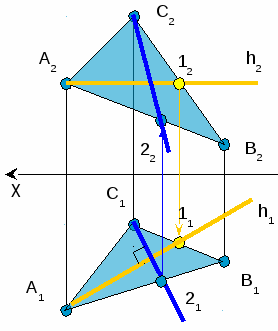
21 20┴ С1 21, 20 21= ∆Z C1 20– Натуральная величина линии ската 
<α= < (С1 21; С1 20) ; <α– искомый  25. опишите алгоритм определения углов между прямой общего положения и плоскостью общего положения. Отобразите в графической форме. Алгоритм:
 Есть еще комбинированный метод но я хз как он делается 26. Опишите алгоритм определения угла между плоскостями общего положения. Отобразите в графической форме. Ответ: 1.Линия пересечения плоскостей  (альфа) и (альфа) и 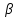 (бетта) = а. (бетта) = а.Проводим плоскость 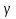 (гамма) перпендикулярную (гамма) перпендикулярную  и и  Построить прямые пересечения 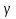 с 2мя плоскостями (m, n) с 2мя плоскостями (m, n)Угол  = угол между m и n ( исходный угол) = угол между m и n ( исходный угол) *************************************************** Мерой угла между плоскостями является острый угол, образованный двумя прямыми, лежащими в этих плоскостях и проведенными перпендикулярно линии их пересечения. Алгоритм:
Примеры: Задача 1 На рисунке представлен случай, когда плоскости α и β заданы следами. Все необходимые построения выполнены согласно алгоритму и описаны ниже. 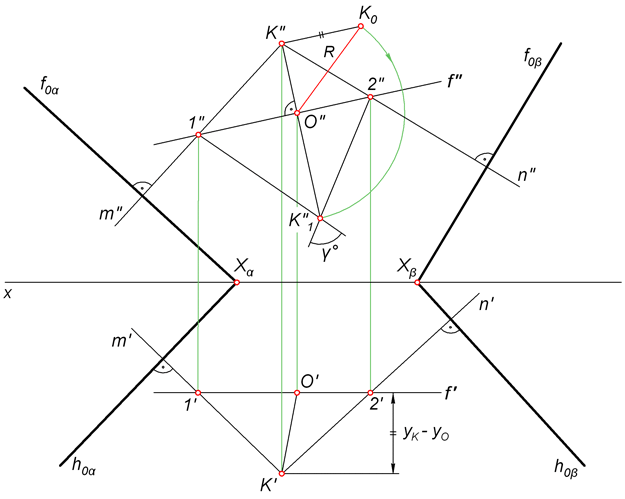 Решение
Задача 2 На рисунке ниже показано решение задачи, в которой требуется найти угол γ° между плоскостями α и β, заданными параллельными и пересекающимися прямыми соответственно. 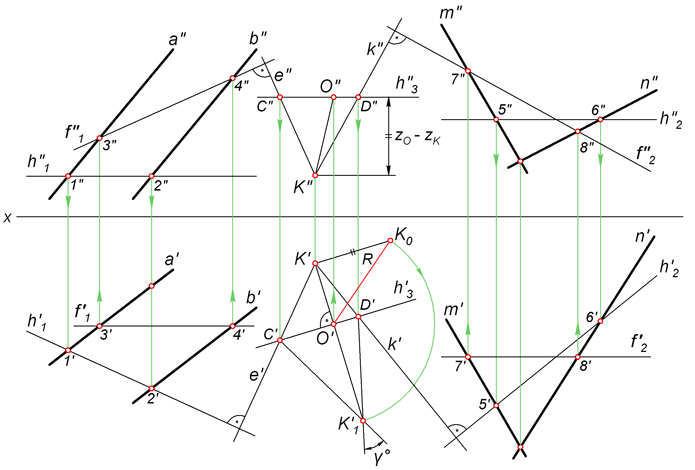 Решение
27. Сформулируйте критерий выбора способа метрических характеристик геометрических фигур в пространстве 1. Расстояние между двумя точками А)Согласно правилу определения натуральных величин Б) способом вращения В) способом замены Г)вращение вокруг прямой уровня Критерий: Точность построения (чем меньше построений, тем точнее) 2. расстояние от точки до прямой А) без преобразования чертежа Б) заменой плоскостей В) вращение вокруг горизонтали |

 – горизонтальный след прямой l,
– горизонтальный след прямой l,  – фронтальный след прямой l, l – индекс принадлежности к линии.
– фронтальный след прямой l, l – индекс принадлежности к линии. ) Точка пересечения с осью Х будет являться фронтальной проекцией горизонтального следа. По линиям связи находим горизонтальную проекцию этой точки.
) Точка пересечения с осью Х будет являться фронтальной проекцией горизонтального следа. По линиям связи находим горизонтальную проекцию этой точки. |
| 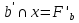 . Полученная точка будет горизонтальной проекцией фронтального следа. Фронтальную проекцию этой точки находят по линии связи.
. Полученная точка будет горизонтальной проекцией фронтального следа. Фронтальную проекцию этой точки находят по линии связи.