ММФ зачет. Вопросы к зачету по ммф 20 Математическая модель
 Скачать 106.77 Kb.
|
|
Вопросы к зачету по ММФ -20 Математическая модель - это приближенное описание посредством математического аппарата (математических символов) различных явлений и процессов. Четыре этапа математического моделирования – 1 этап - начинается с выбора модели, формулировки законов, связывающих основные параметры модели. Он требует знания фактов, относящихся к изучаемым явлениям, знания взаимосвязей между параметрами модели. Заканчивается постановкой краевой задачи, включающей формулировку уравнений, граничных и начальных условий. 2 этап - решение посредством математических методов сформулированной задачи. Методы могут быть аналитическими, численно-аналитическими (когда значительная часть решения прорабатывается аналитически, а затем применяются численные методы) и вычислительными. Понятно, что роль последних постоянно возрастает с развитием вычислительной техники и совершенствованием программного обеспечения. 3 этап - анализ полученных решений и результатов, их физическая интерпретация, сопоставление полученных результатов с известными фактами, которые учитывались при постановке задачи; сравнение с экспериментальными данными. Естественно, это совпадение должно быть в пределах удовлетворяющей нас точности. Высокую точность иногда требовать опасно, - из-за накопления ошибок модель может потерять устойчивость. 4 этап - совершенствование и уточнение исходной модели или построение новой. Этот этап необходим, если полученные результаты нас не удовлетворяют или нам требуется более углубленное изучение явления. Основные уравнения математической физики – уравнения гиперболического, параболического, эллиптического типов Начальные условия – условия, характеризующие процесс в некоторый начальный фиксированный момент времени, с которого начинается изучение этого процесса Граничные условия - т.е. условия на границе той области, в которой протекает процесс. Граничные условия на бесконечности – краевые условия, совокупность начальных и граничных условий Математически корректная постановка задачи - задача считается корректно поставленной, если ее решение удовлетворяет следующим трем требованиям: оно должно существовать, должно быть единственным и устойчивым. Понятие устойчивости решения - означает, что любым малым изменениям входных параметров задачи должны соответствовать малые изменения ее решения. Фактически это означает, что решение должно непрерывно зависеть от начальных и граничных условий, от параметров среды, от частоты и т.д. Уравнение гиперболического типа и процессы, которые оно описывает Свободные колебания Вынужденные колебания Прямая и обратная волны Волны отклонения Волны импульса Суть метода Фурье разделения переменных Постановка задачи о свободных колебаниях ограниченной струны Схема решения задачи о свободных колебаниях ограниченной струны Колебания основного и высшего типов Связь собственных частот струны с её параметрами Постановка задачи для телеграфных уравнений Схема решения телеграфного уравнения в случае линии без потерь Схема решения телеграфного уравнения в случае линии без искажений Физические аналогии в задачах математического моделирования - Для линии передачи с распределенными параметрами  была получена система телеграфных уравнений 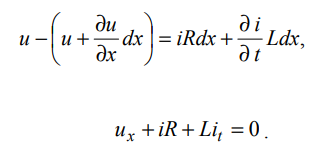 ,  , которая в случае линии без потерь (R = 0, G = 0) имеет вид 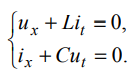Механическим аналогом телеграфных уравнений является система уравнений продольных колебаний стержня 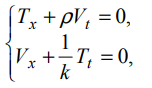 где T– натяжение стержня, V – скорость колебаний, ρ – плотность стержня, k – коэффициент упругости стержня. При изучении движения газа по трубам в случае пренебрежения его трением о стенки трубы имеем систему уравнений газодинамики 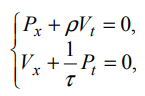 где P – давление газа, V – скорость движения, ρ – плотность газа, τ – коэффициент упругости газа. Уравнения параболического типа и процессы, которые они описывают Простейшее однородное уравнение параболического типа впервые было получено при изучении распространения тепла вдоль однородного металлического стержня. Поэтому его называют также уравнением теплопроводности. Оно имеет вид 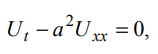 где U(x,t) – функция распределения температуры, x - координата вдоль оси стержня, a = 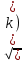 - коэффициент температуропроводности, k - коэффициент теплопроводности, Ρ - плотность стержня, С - удельная теплоемкость металла, из которого выполнен стержень. Начальные и граничные условия в задачах теплопроводности Начальное условие применительно к уравнению теплопроводности заключается в задании распределения температуры по стержню в начальный момент времени, т.е.  Граничные условия должны задаваться в тех точках, в которых возможен теплообмен с окружающей средой. Если боковая поверхность стержня теплоизолирована, а размеры стержня конечны, то теплообмен возможен только через торцы. Пусть торцы стержня имеют координаты x=0, x=l. Самый простой случай граничных условий на торцах, когда они поддерживаются при постоянной температуре, т.е. 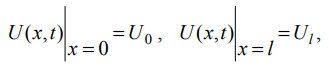 где U0 и Ul – заданные числовые значения температуры. Постановка задач теплопроводности Постановка задачи диффузии и схемы её решения в частных случаях Уравнение эллиптического типа и процессы, которые оно описывает Уравнения Лапласа и Пуассона Уравнение Гельмгольца - функция Дирака и её основные свойства Уравнение Гельмгольца для функции Грина Метод Лапласа асимптотической оценки интегралов Метод перевала асимптотической оценки интегралов в комплексной плоскости Понятие солитона и необходимые условия его существования Солитон – это уединённая волна, распространяющаяся в нелинейной среде с дисперсией и характеризуемая постоянной скоростью распространения и неизменной формой. В отличие от обычных волн, распространяющихся в подобных средах, солитон может существовать сколь угодно долго, испытывая влияние со стороны потерь, если они присутствуют. Солитон, его история, примеры, перспективы использования солитонных режимов понятие солитона возникло в 60-х годах прошлого столетия, открытие этого явления принадлежит англичанину Джону Скотту Расселу (1808 – 1882гг.), изучавшему движение воды в каналах. Нелинейные линии передачи, уравнение Кортевега – де Вриза, его солитонное решение .Нелинейность обусловлена зависимостью индуктивности от тока и емкости от напряжения, начиная, конечно, с некоторых значений амплитуд тока или напряжения. Известен ряд уравнений, имеющих солитонные решения. Одно из них получили Кортевег и де Вриз в 1895 г. при исследовании волн в прямоугольном канале с водой изменяющейся глубины. Это уравнение носит их имена (сокращенно уравнение КдВ) и в его простейшей форме имеет вид  Решение, описывающее солитон, представляет собой функцию 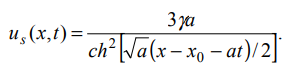 x – координата вдоль направления распространения, x0 – координата образования солитона t – время; a = x /t – скорость движения солитона; u(x,t) – амплитуда или высота солитона. Основные свойства и параметры солитона Интегральные уравнения, понятия, типы Интегральные уравнения Фредгольма и Вольтерра Схема метода интегральных преобразований Интегральные преобразования Фурье и Лапласа Свёртка функций и теорема о свёртке Лемма Жордана и теорема Коши о вычетах |