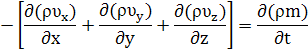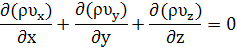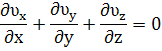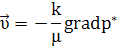Вопросы Гидро механики. Вопросы по дисциплине Подземная гидромеханика
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
градиенту потенциальной функции (потенциала скорости).Вопросы по дисциплине «Подземная гидромеханика» Этапы развития подземной гидромеханики. Нефтяная ПГ возникла на основе гидромеханики подземных вод. Вопросы движения подземных вод в различное время изучали М.В.Ломоносов, Д.Бернулли, Л.Эйлер и др., проводившие свои работы в Петербургской Академии наук. Начало развития ПГ как самостоятельно науки было положено французским инженером Анри Дарси (1805-1866), который в 1856г. сформулировал и опубликовал обнаруженный им экспериментальный закон ламинарной фильтрации. Однако до 90-х годов дельной теории о движении подземных вод как таковой не было. Лишь в 1889 г. работой профессора Жуковского Николая Егоровича (1847 – 1921) «Теоретические исследования о движении подпочвенных вод» заложен фундамент такой теории. В 1912 году вышла из печати работа А.А. Краснопольского, в которой изложена теория притока воды к колодцам при турбулентной фильтрации. В начале 20-х годов нашего столетия в ответ на потребности бурно развивающейся нефтяной промышленности было положено начало созданию нового направления ПГ – нефтяная (или нефтегазовая) подземная гидродинамика. Основателем этого направления в теории фильтрации в СССР стал академик Л.С. Лейбензон. Его исследования были начаты в 1921 г. и продолжались в течение 30 лет (до его кончины в 1951 г.). Работы Лейбензона прочно закрепили приоритет отечественной науки – ПГ. Академик Л.С. Лейбензон был создателем «Подземной гидравлики» и как учебной дисциплины, курс которой впервые читался им в Московской горной академии в 1927 – 1928 гг. Развитие нефтегазовой подземной гидромеханики в нашей стране связано с именем многочисленных учеников академика Л.С. Лейбензона. Выдающейся вклад в развитие теории фильтрации в нефтегазоводоносных пластах внесли академик С.А. Христианович, профессор Б.Б. Лапук, И.А. Чарный, В.Н. Щелкачев. Написанные ими монографии и учебники стали классическими и основополагающими. Теория фильтрации. Скорость фильтрации и ее связь со скоростью движения. Под пористой средой следует понимать материальное тело, содержащее в себе пустоты в виде мельчайших пор, трещин, каверн, карстовых образований (множество твердых частиц, тесно прилегающих друг к другу, сцементированных или не сцементированных, пространство между которыми (поры, трещины) может быть заполнено жидкостью или газом). Поры могут быть сообщающимися и не сообщающимися. Пористые материалы по их структуре разделяют на неупорядоченные (естественные пористые среды) и упорядоченные (фиктивный и идеальный грунты) Фиктивный грунт – грунт (система), составленный из шариков одинакового диаметра при правильной упаковке. Идеальный грунт — система цилиндрических поровых каналов одинакового диаметра и параллельных друг другу. При изучении микродвижения жидкости в пористой среде пользуются понятием средней истинной скорости движения жидкости 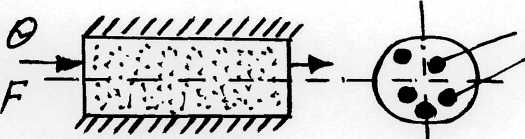 Площадь фильтрации - суммарная площадь пустот и зерен, находящихся в данном поперечном сечении. При изучении общей картины движения жидкости в пористых средах пользуются понятием скорости фильтрации – v. Скорость фильтрации - это такая воображаемая скорость, с которой двигалась бы жидкость между кровлей и подошвой пласта, если бы самой пористой среды не было. 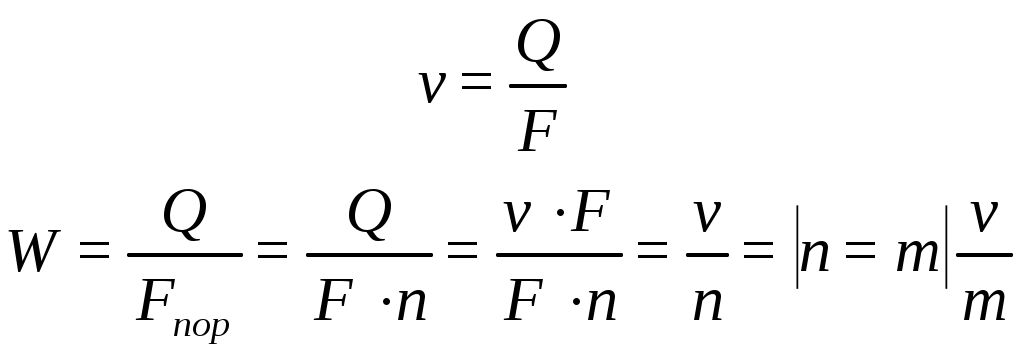 Линейный закон фильтрации Дарси. Основное соотношение теории фильтрации – закон фильтрации – устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрацион¬ное течение. Н1 и Н2 – полные напоры на входе и выходе образца породы (модели пласта), ∆Н = Н1 – Н2 – потери напора. k ф – характеризует расход потока через единицу площади сечения, пер-пендикулярного к потоку, под действием единичного градиента напора. 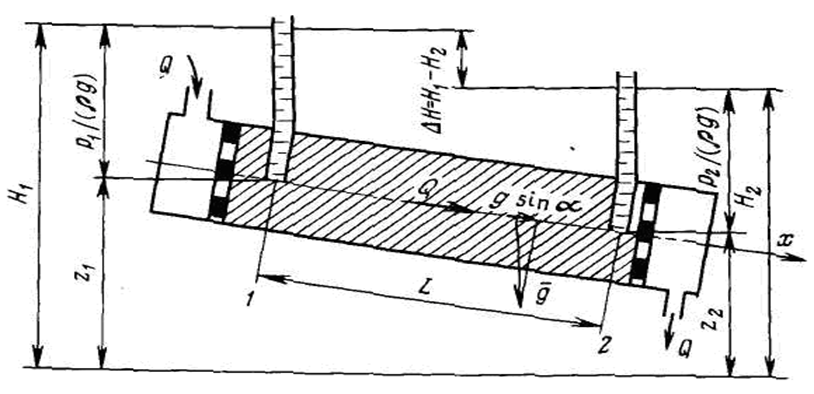 Рис. 1. Схема пермеаметра Скорость фильтрации |
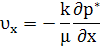 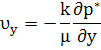 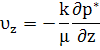 | 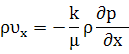 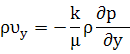 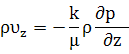 |
Введем понятие потенциальная функция течения Ф (потенциал скорости фильтрации):
тогда
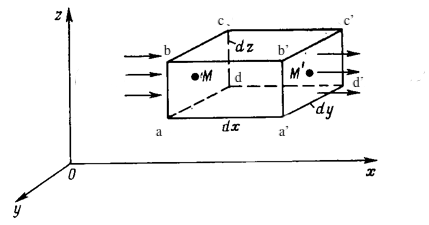
Подставив проекции вектора массовой скорости фильтрации в уравнение неразрывности, получим его в новом виде:
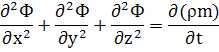
Уравнения состояния жидкостей, газов и пористой среды.
Выведенные выше дифференциальные уравнения содержат такие пара-метры, как k, m, ρ , μ . Для дальнейших расчетов надо знать зависимость этих параметров от давления Р. При изотермическом процессе фильтрации такая за-висимость, выражающая состояние жидкости, газа (или их смеси) и пла-ста, называется уравнением состояния.
Рассмотрим уравнения состояния для жидкостей, газов и пористых сред.
А) для жидкостей.
Для больших изменений давления от начального значения P0 до текущего значения P плотность жидкости определяется по формуле:
ρ = ρо• e βж (Р–Ро)
где βж – коэффициент объемного сжатия жидкости (коэффициент сжима-емости).
При определении плотности жидкости для малых изменений давления Р пользуются следующей формулой:
ρ = ρо• (1+βж (Р–Ро) .
На вязкость нефти μ большое влияние оказывает to. Эксперименты пока-зывают, что с повышением давления Р (при Р>Рнас) μ нефти увеличивается:
Здесь μ 0 – вязкость при фиксированном давлении Р0, αμ – эксперимен-тальный коэффициент, зависящий от состава нефти.
Б) для газов.
Природные газы можно считать идеальными (совершенными), если пла-стовые давления газовых месторождений невелики (до 6 – 9 МПа) и газ отби-рается при депрессии на пласт до 1 МПа.
Зависимость z(Р) при постоянной температуре можно считать экспонен-циальной при больших изменениях давления:
и линейной при малых изменениях давления:
где z0 – коэффициент сверхсжимаемости при Р0.
Зависимость μ =μ (Р) для газов можно представить аналогично для жид-кости.
В) для пористых сред.
При малых изменениях Р уравнение состояния пористой среды
где m0 – коэффициент пористости при Р0.
При значительных изменениях давления Р изменение пористости описы-вается уравнением
Экспериментально установлено, что не только пористость, но и проница-емость существенно изменяются с изменением пластового давления, причем часто проницаемость значительнее, чем пористость. При малых изменениях давления Р эту зависимость можно принять линейной:
а при больших – экспоненциальной:
В трещиноватых пластах проницаемость изменяется в зависимости от давления более интенсивно, чем в пористых. Поэтому в трещиноватых пластах учет зависимости k(Р) более необходим, чем в гранулярных.
Дифференциальные уравнения установившейся фильтрации несжимаемой жидкости по закону Дарси.
Краевые задачи ПГ (определение и порядок решения). Упрощения и допущения, принятые при решении задач ПГ.
Численный подход к математической обработке результатов измерений, полученных при эксплуатации нефтяной скважины, основан на применении теории обратных задач математической физики и хорошо зарекомендовал себя при решении ряда задач.

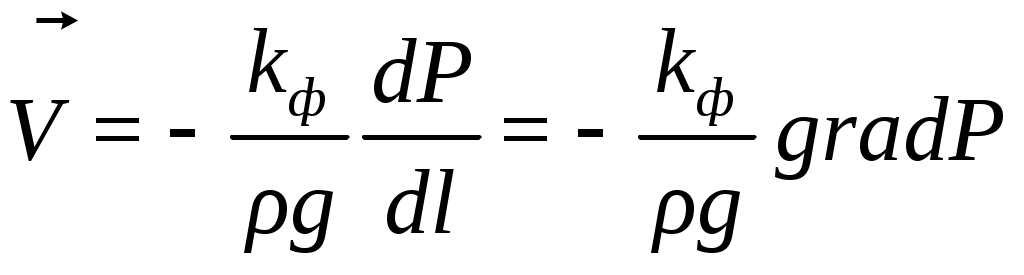
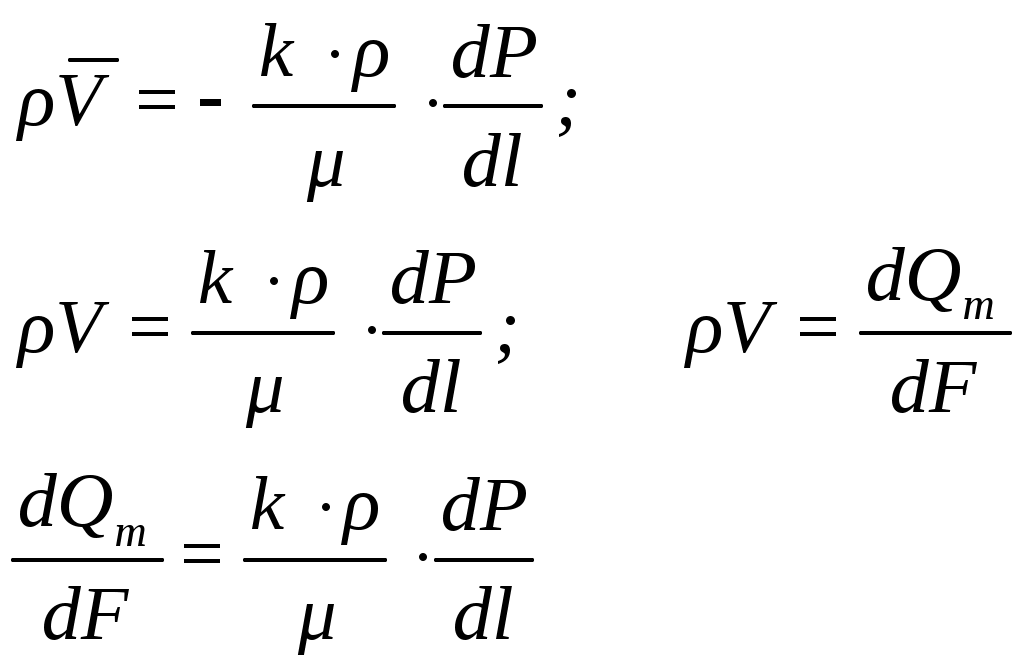
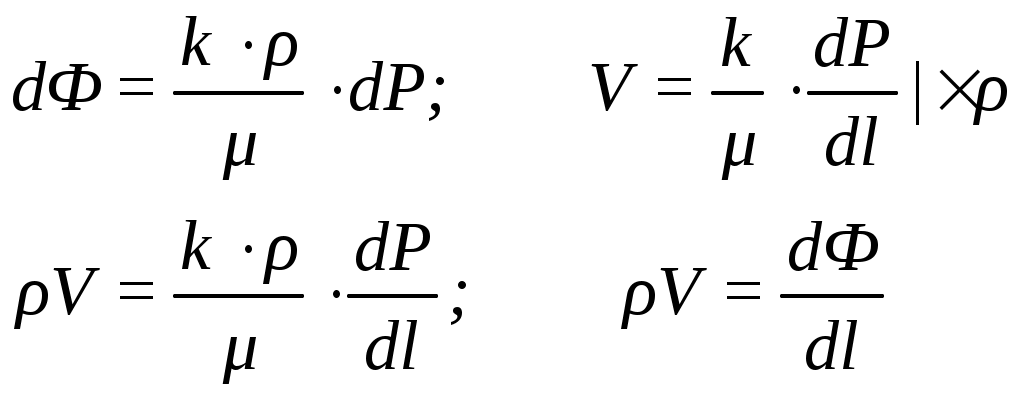
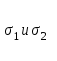 - насыщенности соответственно смачивающей и несмачивающей фаз.
- насыщенности соответственно смачивающей и несмачивающей фаз.