Вариант 55. Задача 1 (6). По предложенному вам дирекционному углу ( 152 градуса), определите следующие данные
 Скачать 184.23 Kb. Скачать 184.23 Kb.
|
Задача 1 (6). По предложенному вам дирекционному углу (α = 152 градуса), определите следующие данные: 1) Азимут истинный; 2) Азимут истинный обратный; 3) Азимут магнитный на данный год; 4) Азимут магнитный на данный год обратный; 5) Румб истинный; 6) Румб истинный обратный; 7) Румб магнитный; 8) Румб магнитный обратный. Азимут истинный – это горизонтальный угол, измеряемый по ходу часовой стрелки между северным направлением истинного (географического) меридиана и направлением на предмет: Аист. = α + γ где γ – сближение меридианов – это угол между северным направлением истинного меридиана и вертикальной линией координатной сетки; α – дирекционный угол. Для листа карты М 1 : 10000 среднее сближение меридианов западное 2о22′, то есть (–2о22′). Подставляя эти данные в формулу получаем: Аист. = 152о + (–2о22′) = 152о – 2о22′ = 149о38′ Азимут магнитный – горизонтальный угол, измеряемый по ходу часовой стрелки между северным направлением магнитного меридиана и направлением на предмет: Амаг. = α – ПН где α – дирекционный угол; ПН – поправка направления, находится по формуле: ПН = δ – γ где δ – магнитное склонение; γ – сближение меридианов. Вычисляем магнитное склонение на данный (2021) год. Известно, что склонение на 1971 год восточное: δ = +6о12′ Среднее сближение меридианов западное: γ = –2о22′ Годовое изменение склонения восточное. За один год: δ = +0о02′ Разница в годах составляет: Δ = 2021 – 1971 = 50 лет Годовое изменение склонения за 50 лет: 50 ∙ 0о02′ = 1о40′ Таким образом, магнитное склонение: δ = 1о40′ + 6о12′ = +7о52′ Поправка направления: ПН = +7о52′ – (–2о22′) = 7о52′ + 2о22′ = 10о14′ Магнитный азимут: Амаг. = 152о – 10о14′ = 141о46′ Румб – это угол, отсчитываемый от ближайшего (северного или южного) направления меридиана по ходу или против хода часовой стрелки до данного направления. Величина румба не превышает 90о. Румб истинный отсчитывают от истинного меридиана. По табл. 2 (связь между азимутами и румбами) имеем: Аист. = 149о38′ – это вторая четверть (ЮВ), значит: rист. = 180о – Аист. = 180о – 149о38′ = ЮВ: 30о22′ Румб магнитный отсчитывают от магнитного меридиана. Аналогично: rмаг. = 180о – Амаг. = 180 – 141о46′ = ЮВ: 38о14′ Азимут истинный обратный и азимут магнитный обратный определяем по табл.3 (зависимость азимута прямого и обратного): Аист = 149о38′ – это вторая четверть, Амаг = 141о46′ – это тоже вторая четверть, значит: Аист. обр. = Аист. + 180о = 149о38′ + 180о = 329о38′ Амаг. обр. = Амаг. + 180о = 141о46′ + 180о = 321о46′ Определяем румб истинный обратный и румб магнитный обратный, учитывая что румб обратный равен румбу прямому по значению, но противоположному по направлению: rист. = ЮВ: 30о22′ → rист. обр. = СЗ: 30о22′ rмаг. = ЮВ: 38о14′ → rмаг. обр. = СЗ: 38о14′ Ответ: 1) Аист. = 149о38′; 2) Аист. обр. = 329о38′ ; 3) Амаг. = 141о46′; 4) Амаг. обр. = 321о46′; 5) rист. = ЮВ: 30о22′; 6) rист. обр. = СЗ: 30о22′; 7) rмаг. = ЮВ: 38о14′; 8) rмаг. обр. = СЗ: 38о14′ Задача 2 (37). Постройте линейный и поперечный масштабы для численного 1:5000. Укажите на них длину линии местности в 675,0 м. Определите по поперечному масштабу длину линии местности, если на плане в данном масштабе она составила 7,56 см Численный масштаб 1:5000 означает, что один сантиметр на карте соответствует 5000 сантиметрам в реальности. 5000 сантиметров – это 50 метров (так как в 1 метре укладывается 100 сантиметров). Если записать этот масштаб в численном виде, то он будет выглядеть так: в 1 см 50 м (в одном сантиметре 50 метров). Линейный масштаб: 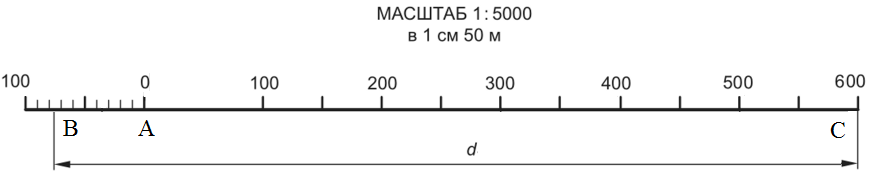 Расстояние на местности: d = ВС = АС + АВ = 600 м + 75 м = 675 м Длина линии местности: L = ВС = АС + АВ = 12 см + 1,5 см = 13,5 см Для того чтобы в поперечном масштабе 1 : 5000 отложить длину, равную на местности 675 м, правую ножку циркуля-измерителя совмещаем с точкой 600 м справа от нуля, а левую с точкой 70 м слева от нуля. Затем измеритель поднимаем на пять делений вверх (5 м) и раздвигаем до точки, соответствующей 675 м. Поперечный масштаб: 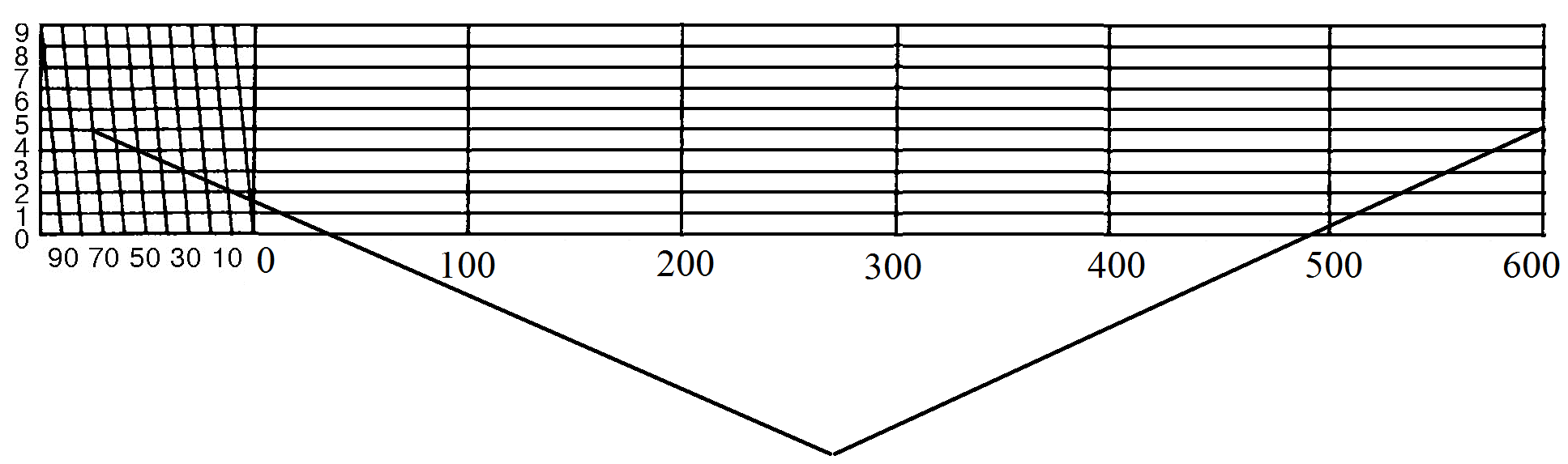 Отрезок длиной 7,56 см занимает 3 целых основания, 7 десятых долей основания и 8 сотых долей основания: 7,56 см : 2 см = 3 1,56 см : 0,2 см = 7 0,16 см : 0,02 см = 8 Так как длина одного целого основания равна 2 см, то при масштабе 1:5000 оно будет составлять 100 м на местности. Соответственно одна десятая доля будет составлять на местности 10 м, а одна сотая доля – 1 м. Из этого следует, что длина нашего отрезка на местности будет составлять: 100 м ∙ 3 + 10 м ∙ 7 + 1 м ∙ 8 = 378 м Ответ: длина линии местности в 675,0 м составляет 13,5 см; линия на плане в данном масштабе 7,56 см соответствует длине линии местности 378 м. Задача 3 (45). Определите длину линии местности, недоступную для измерения, если она образует треугольник со сторонами, непосредственное измерение которых показало 484,27 и 695,12 м, а угол между ними 122о30′. Используя теоремы косинусов и синусов, находим длину стороны треугольника: с2 = а2 + b2 – 2 ∙ a ∙ b ∙ cosγ = = 484,272 + 695,122 – 2 ∙ 484,27 ∙ 695,12 ∙ cos122о30′ = 1079447 м 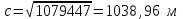 Находим значения синусов углов: sin α = а ∙ sin γ/с = 484,27 ∙ sin122о30′ / 1038,96 = 0,3931 sin β = b ∙ sin γ/c = 695,12 ∙ sin122о30′ / 1038,96 = 0,5642 Что соответствует значениям углов: α = 23о8′ β = 34о21′ Ответ: длина линии местности, недоступная для измерения, составляет 1038,96 м Задача 4 (70). Для точки К с географическими координатами: широтой φ, долготой λ, указанными в таблице, определить: 1) номенклатурное обозначение листа топографической карты масштаба 1:10000, на котором изображается точка К; 2) географические широту и долготу сторон рамки (трапеции) обозначенного листа карты.
По рисунку 5 методических указаний определяем по широте точки букву латинского алфавита, обозначающую ряд, а по долготе – номер колонны. По схемам находим, что точка К изображается на листе N-35 топографической карты масштаба 1:1000000. Составляем общую схему (контур) листа N-35 и указываем широту φю и φс южной и северной сторон, долготу λз и λв западной и восточной сторон его рамки по исходной схеме. 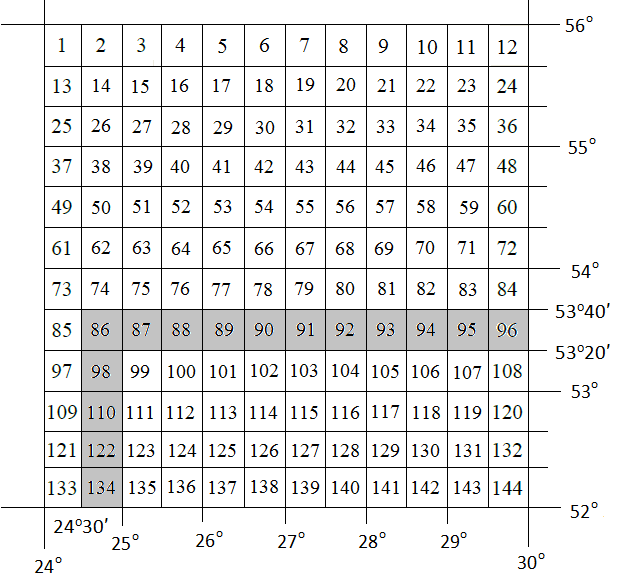 Схема разграфки листа карты масштаба 1:100000 Для определения номенклатуры и географических координат отдельных листов многолистной карты масштаба 1:100000 схема листа N-35 разграфляется на 12 колонок линиями меридианов и на 12 поясов линиями параллелей. На полученной схеме подписана широта каждой параллели через 20′ и указана долгота каждого меридиана через 30′. Каждый лист карты масштаба 1:100000 нумеруется по порядку от 1 до 144. В нашем примере точка К изображается на листе N-35-86. Составив укрупненную схему листа, переходим к определению географических координат сторон рамок и номенклатуры листов топографических карт более крупных масштабов. Лист карты масштаба 1:50000 образуется делением листа карты масштаба 1:100000 на четыре части; его номенклатура состоит из номенклатуры стотысячной карты и одной из заглавных букв А, Б, В, Г русского алфавита. По значениям φк и λк определяем, что пункт К карты масштаба 1:50000 изображается на листе: N-35-86-В 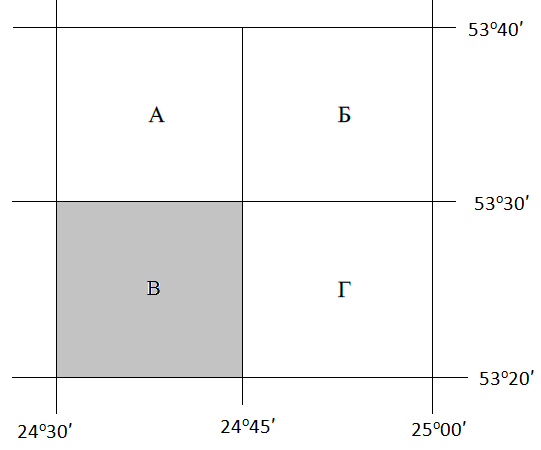 Схема разграфки листа карты масштаба 1:50000 Листы карты масштаба 1:25000 получают делением листов карты масштаба 1:50000 на четыре части, каждая из которых обозначается строчными буквами русского алфавита (а, б, в, г). Размеры этих листов по широте составляют 5′, по долготе – 7′30″, а номенклатура дополняется соответствующей буквой. Наш пункт К изображается на листе N-35-86-В-в карты масштаба 1:25000. 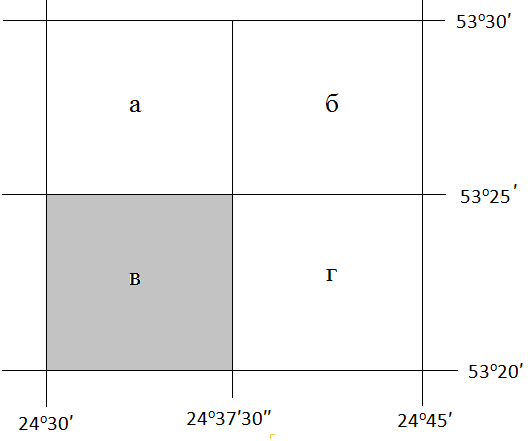 Схема разграфки листа карты масштаба 1:25000 Лист карты масштаба 1:25000 делится на четыре листа карты масштаба 1:10000, каждый из которых имеет размеры по широте 2′30″, по долготе 3′45″. Они обозначаются арабскими цифрами (1, 2, 3, 4). Номенклатура листа карты масштаба 1:10000 – N-35-86-В-в-1 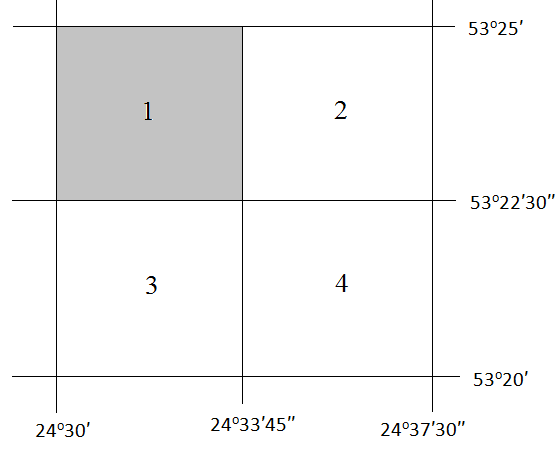 Схема разграфки листа карты масштаба 1:10000 ОТВЕТ: Лист топографической карты N-35-86-В-в-1 масштаба 1:10000 расположен между параллелями с широтой φс = 53о25′, φю = 53о22′30′′; меридианами с долготой λз = 24о30′, λв = 24о33′45′′. Задача 5 (90). а) Определите географические и прямоугольные координаты предложенного пункта в заданном квадрате топографической карты (масштаб карты 1: 25 000): ключ Белый с отметкой 144,3 м в квадрате 6513. б) Определите уклон линии и крутизну ската по тригонометрической и приближенной формулам от глиняного карьера (6513) на родник у отметки 147,0 м (6612) а) Измерение по карте географических координат точки сводится к проведению через нее параллели и меридиана и отсчету их широты и долготы на соответствующих сторонах минутной рамки. Уложив на листе карты линейку так, чтобы ее ребро проходило через данную точку и одноименные деления на западной и восточной сторонах минутной рамки, отсчитывают по одной из них широту точки. Аналогично, пользуясь северной и южной сторонами минутной рамки, отсчитывают ее долготу. Географические координаты предложенного пункта: λ = 18о06′28′′ φ = 54о40′32′′ Определяем прямоугольные координаты предложенного пункта. Сначала записываем (в километрах) абсциссу южной стороны квадрата, в котором находится эта точка (т.е. 6065). Затем измеряемв масштабе карты длину перпендикуляра, опущенного из точки на эту линию. Полученную величину (в данном случае 100 м) добавляем к абсциссе линии. Число 6065100 м есть абсцисса Х предложенного пункта. Ордината точки равна ординате западной стороны того же квадрата (в километрах), сложенной с длиной перпендикуляра (в данном случае 400 м), измеренного по карте. Число 4313400 м есть ордината У предложенного пункта. б) Определяем отметку точки А (глиняный карьер). Измеряем линейкой x (расстояние от младшей горизонтали до данной точки) = 1 мм и d (расстояние на карте между двумя последовательными горизонталями, проходящее через нашу точку А) = 5 мм. Определяем высоту сечения рельефа (h), которая указана внизу на карте под масштабом = 5 м. Отметка младшей горизонтали равна 144,3 м. Все данные подставляем в формулу и находим превышение точки над младшей горизонталью: 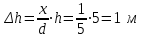 Теперь находим отметку точки А по формуле: HА = Hn+ Δh = 144,3 м + 1 м = 145,3 м где Hn – отметка младшей горизонтали. Таким образом, отметка точки А (глиняный карьер) равна 145,3 м, отметка точки В равна 147,0 м (по заданию). Разность отметок между крайними точками линии АВ равна: h = 147,0 м – 145,3 м = 1,7 м Длина линии равна 7,5 см (измеряем по карте), а так как масштаб карты (в данном примере) 1:25000, то в 1 см 250 м, т. е. рассточние между точками: d = 7,5 см ∙ 250 = 1875 м Следовательно, средний уклон заданной линии равен: 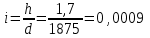 в процентах: 0,0009 ∙ 100 = 0,09 % в промилле: 0,0009 ∙ 1000 = 0,9 ‰ Определяем крутизну ската по тригонометрической формуле: 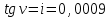 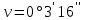 Определяем крутизну ската по приближенной формуле: 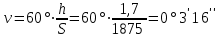 Задача 6 (110). По данным своего варианта постройте буссольный полигон, произведите увязку буссольного полигона способом параллельных линий и определите его площадь геометрическим способом (методом треугольников). Перед построением полигона определите горизонтальное проложение линий. Масштаб 1:2000
Вычисляем горизонтальные проложения S сторон буссольного хода для тех сторон, которые имеют углы наклона: S = D ∙ cosν где ν – угол наклона линии к горизонту; D – длины наклонной линии на местности. Горизонтальные проложения заносим в соответствующую графу журнала буссольной съемки. Если угол наклона равен 0°, то горизонтальное проложение будет таким же, как и длина линии. Переносим такие же данные в графу «горизонтальные проложения». S4–5 = 135,5 ∙ cos6о = 134,8 м S5–6 = 216,4 ∙ cos7о = 214,8 м Рассчитаем периметр хода Р (сумма горизонтальных проложений): Р = 129,0 + 153,6 + 173,2 + 134,8 + 214,8 + 120,4 + 127,6 = 1053,4 м Строим буссольный полигон по румбам и горизонтальным проложениям. Определяем абсолютную невязку. Она равна 1 мм, что соответствует 2 м на местности для выбранного масштаба. Относительную невязку определяем по формуле: 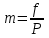 где: m – относительная невязка; f – абсолютная невязка; Р – периметр участка. 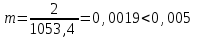 Следовательно, невязка получилась допустимой. Невязка распределяется пропорционально длинам линий в следующем порядке. Полученная невязка 2 м приходится на весь периметр участка. Так как в данном периметре (1053,4 м) 105 десятков, то поправка, приходящаяся на один десяток, будет равна 2 : 105 = 0,019 м. Длину первой линии округляем до 13 десятков, и, следовательно, поправка на эту линию будет равна 13 х 0,019 = 0,247 м, а на вторую линию, длина которой берется равной 15 десяткам, поправка составляет 15 х 0,019 = 0,285 м. Также распределяются невязки и по остальным линиям, чтобы сумма всех поправок была равна 2 м (распределение невязки ведется до десятых долей метра).
После вычисления поправок на каждую точку передвигаем все точки, кроме первой, на соответствующую величину поправки. Для этого определяем направление невязки путем соединения последней полученной точки 1 с точкой 1′ и в этом направлении прочерчиваем линию с указанием направления невязки. Затем из всех остальных вершин участка проводим линии в том же направлении Увязанный чертеж полигона представлен в приложении 1 в масштабе 1:2000. Определяем площадь полученного полигона методом треугольников. Получившийся полигон представляет собой многоугольник, соответственно его делят тонкими линиями на треугольники, в которых графически, с учетом масштаба определяем основание и высоту. Затем по формуле из геометрии высчитываем площадь: 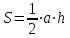 где a – основание треугольника, h – высота треугольника. Результаты вычислений оформляем в виде таблицы:
Ход определения площади полученного полигона методом треугольников представлен в приложении 2 в масштабе 1:2000. Задача 7 (135). Раскройте содержание работ по подготовке трассы к нивелированию и разбивке пикетажа. Строительству комплексов линейных сооружений, как известно, предшествует составление проекта. Для этого необходимо иметь данные об относительных высотах точек местности как по оси трассы и в пределах полосы, занимаемой линейным сооружением так и на площадках, отводимых под строительство сооружений проектируемого комплекса. Эти данные характеризуют естественный рельеф местности, который, как правило, не удовлетворяет требованиям рационального размещения сооружений и эксплуатации безнапорных трубопроводов. Уклоны естественного рельефа могут превышать требуемые допуски по осям сооружения. При наличии плоского рельефа могут возникнуть затруднения в организации стока ливневых вод и канализации. Линейные сооружения на них занимают по ширине сравнительно узкую полосу. В связи с этим нивелирование вдоль трассы таких линейных сооружений называют продольными. На каждом объекте строительства необходимо с требуемой детальностью и точностью получить отметки заемной поверхности на расстоянии одна от другой 100 м и менее по оси трассы. По полученным отметкам точек и расстояниям между ними составляют продольный профиль трассы, необходимый для проектирования линейного сооружения. Ходы продольного нивелирования привязывают к реперам и пунктам государственной нивелирной сети. Это необходимо для того, чтобы, во-первых, на строительной площадке и по трассе проектируемого трубопровода получить отметки реперов и пунктов сгущения в единой государственной системе высот и, во-вторых, произвести контроль и оценку точности полученных результатов. Продольное нивелирование при строительстве ведут по особой программе, хотя и обычным методом геометрического нивелирования. Продольное нивелирование включает следующие этапы работ: получение задания; рекогносцировка трассы; разбивка пикетажа; нивелирование трассы; увязка превышений и вычисление отметок точек; составление профиля трассы. Получив задание на продольное нивелирование, подбирают необходимый плановый и высотный материал для района производства работ. По высотному материалу выбирают те из ближайших пунктов и реперов государственной высотной основы, к которым ближайшим путем и с требуемой точностью будут привязаны концы ходов продольного нивелирования. Рекогносцировку трассы выполняют на местности для уточнения выбранного направления, выбора углов поворота трассы, проверки наличия и сохранности реперов, привязки ходов с учетом технической и экономической целесообразности при проведении строительства. Перед нивелированием трассы проводят подготовительные работы. Для чего по оси будущего сооружения, по кольям и столбам, закрепляющим вершины углов поворота трассы, прокладывают теодолитный ход. Углы в поворота хода измеряют теодолитом, длины D линий – стальной мерной лентой. Вершины углов поворота обозначают ВУ1, ВУ2 и т.д. Разбивка пикетажа по трассе состоит в откладывании по оси будущего сооружения отрезков, горизонтальные положения которых равны 100 м (иногда 60 и 40 м). Эти отрезки называют пикетами. Конец каждого пикета, закрепленного деревянным колышком длиной 15 – 25 см, забитым вровень с землей, называют пикетной точкой (или пикетом). Рядом с пикетным колышком забивают второй – сторожек, несколько выступающий над землей; на сторожке обозначают номер пикета. Начало трассы обозначают ПК0 (пикет нуль), последующие – ПК1, ПК2,… и т.д. Поэтому по номеру каждого пикета легко определяется число сотен метров трассы от ее начала. Характерные точки излома рельефа местности между пикетами, а также пересечения трассой границ угодий, ручьев, рек, озер, надземных сооружений, подземных коммуникаций и т.п. тоже отмечают колышками. Эти точки называют плюсовыми (или промежуточными), так как их местоположение на трассе определяется расстоянием от пройденного заднего пикета. Например ПК3 + 48 означает, что данная плюсовая точка находится между ПК3 и ПК4 на трассе в 48 м от ПК3. При разбивке пикетажа результаты всех измерений заносят в пикетажную книжку, в которой указывают значения углов поворота трассы, номера всех пикетов и плюсовых точек, а также зарисовывают абрис глазомерной съемки и полосы земной поверхности вдоль трассы. В местах, где будут построены сооружения, или через определенные расстояния вдоль трассы, а также на углах ее поворота устанавливают временные реперы, размещения их за пределами будущих земляных работ. Список литературы 1. Булеков, И.Ф. Таблицы для вычисления приращений прямоугольных координат с контролем: научное издание / И.Ф. Булеков. М.: Недра, 1974 - 256 с. 2. Дубов, С.Д. Геодезия / С.Д. Дубов, А.Н. Поляков. М.: Агропромиздат, 1988 - 237 с. 3. Дубов, С.Д. Практикум по геодезии / С.Д. Дубов, А.Н. Поляков. М.: Агропромиздат, 1990 - 214 с. 4. Нестеренок, В.Ф. Геодезия в лесном хозяйстве : учеб. пособие / В.Ф. Нестеренок. Минск : РИПО, 2015 - 280 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
