Механика КМРК 44 вариант. Теор.механика вар 44. Задача 4 3 Задача 14 8 Задача 24 12 Задача 34 15 Задача 44 19 Решение 21 Участок ас. Ход слева. 22
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Содержание Задача 4 3 Задача 14 8 Задача 24 12 Задача 34 15 Задача 44 19 Решение 21 Участок АС. Ход слева. 22 Участок СD. Ход слева. 22 Участок EВ. Ход справа. 22 Участок ВD. Ход справа. 22 Подбор сечения из двух швеллеров производим из условия прочности по формуле: 23 Для одного швеллера 23 . 23 Задача 54 24 Список используемой литературы 31 Задача 4Определить реакции стержней, удерживающих грузы F1 и F2. Массой стержней пренебречь. Схему своего варианта см. на рисунке – 1. Числовые данные своего варианта взять из таблицы – 2. Дано: 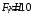 , ,  , схема 4. , схема 4.Найти:  , ,  . .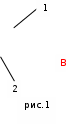 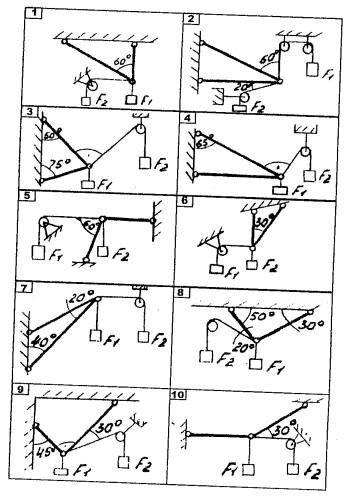 Решение Рассмотрим равновесие шарнира В (рис.1). Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис.2)  Выбираем систему координат и составляем уравнения равновесия для системы сил, действующих на шарнир В:  ; ; 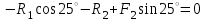 ; (1) ; (1) ; ; 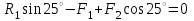 . (2) . (2)Определяем реакции стержней R1и R2, решая уравнения (1), (2). Из уравнения 2: 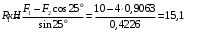 . .Из уравнения 1: 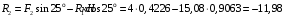 . .Знак минус перед значением 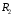 указывает на то, что первоначально выбранное направление реакции неверное, направляем реакцию указывает на то, что первоначально выбранное направление реакции неверное, направляем реакцию 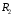 в противоположную сторону, т. е. к шарниру В (на рис. 2 истинное направление реакции в противоположную сторону, т. е. к шарниру В (на рис. 2 истинное направление реакции 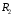 показано штриховым вектором). показано штриховым вектором).Проверяем правильность полученных результатов, решая задачу графически (рис.3). Полученная система сил (рис.2) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым. Строим силовой многоугольник в следующем порядке (рис. 3):в выбранном масштабе 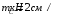 откладываем заданную силу откладываем заданную силу 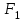 ( (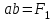 ), затем из точки bпод углом 25° к вертикали откладываем силу ), затем из точки bпод углом 25° к вертикали откладываем силу  ( (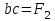 ), далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке dиврезультате построения образуется замкнутый многоугольник abсd, в котором сторона ), далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке dиврезультате построения образуется замкнутый многоугольник abсd, в котором сторона 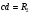 , а сторона , а сторона 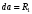 . Измерив длины этих сторон (в мм) и умножив на масштаб построения, получаем значения реакций стержней: . Измерив длины этих сторон (в мм) и умножив на масштаб построения, получаем значения реакций стержней:  , , 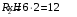 . . Вычислим допущенную при графическом способе решения ошибку: 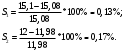 (Ошибка находится в пределах 2%). Ответ: а) аналитическое решение:  ; ; 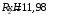 . . б) графическое решение: 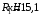 ; ; 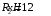 . . Задача 14Для заданного сечения, составленного из приваренных друг к другу прокатных профилей, определить положение центра тяжести (рисунок – 2, таблица – 3). Дано: 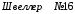 , , 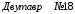 , схема 14. , схема 14.Найти: 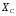 , , 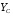 . .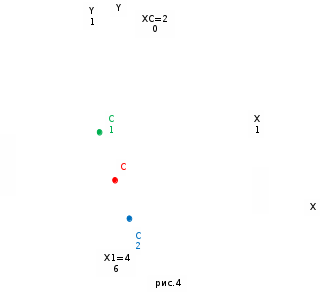  Решение Разобьем сечение на две составные части и обозначаем центры тяжести, которые для прокатного профиля принимаем по сортаменту (рис.4): 1 – швеллер №16 с центром тяжести 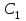 ; ;2– двутавр №18 с центром тяжести  . .Выписываем из таблиц сортамента прокатной стали по ГОСТ 8239-89, ГОСТ 8240-89, необходимые геометрические характеристики составных частей сечения Швеллер №16: 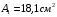 ; ; 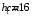 ; ; 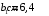 ; ; 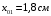 . .Двутавр №18: 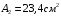 ; ; 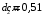 . .Выбираем оси координат, как показано на рис.4. Начало координат поместим в центр тяжести двутавра 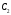 . .Определяем ординаты центров тяжести составных частей сечения в выбранной системе координат и площадь всего сечения. а) швеллер 1: 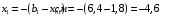 ; ;  ; ; б) двутавр2: 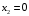 ; ;  . .Площадь всего сечения 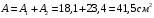 . .Определяем координаты центра тяжести сечения по формулам:  , ,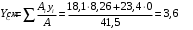 . .Изображаем положение центра тяжести С сечения на рис.4. Его координаты ( 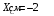 ; ; ). ).Ответ: 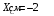 ; ;  . . Задача 24Груз массой m, двигаясь по наклонной плоскости (рисунок - 3, схема I) или по горизонтальной плоскости (рисунок - 3, схема II), под действием силы F проходит путь S за время t. Считая движение груза равноускоренным с начальной скоростью V0 = 0 м/с, определить величину силы F, если коэффициент трения равен f. Исходные данные для своего варианта взять из таблицы - 4. Дано:  , , 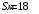 , , 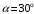 , , 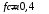 , , 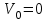 , , 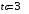 , схема 2. , схема 2.Найти: 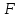 . .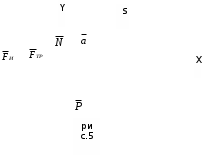  Решение Принимаем груз за материальную точку и указываем направление ускорение 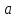 этой точки (рис.5). этой точки (рис.5).Прикладываем к точке все активные силы, действующие на груз:  вес груза; вес груза; 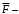 приложенная сила; приложенная сила; 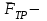 сила трения. сила трения.Освобождаем точку от связей, заменив их действие реакциями:  реакция опорной поверхности. реакция опорной поверхности.Добавляем к этой силе силу инерции 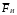 , направленную противоположно ускорению , направленную противоположно ускорению 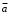 . .Согласно принципу Даламбера силы 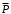 , , 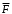 , , 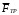 и и 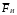 образуют уравновешенную систему сил. Составляем уравнения равновесия статики: образуют уравновешенную систему сил. Составляем уравнения равновесия статики: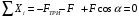 ; (1) ; (1)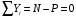 . (2) . (2)Записываем формулы для определения сил и ускорения точки  , ,  , , 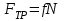 , , 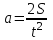 . (3) . (3)Выражаем  из уравнения (2) из уравнения (2) 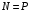 и подставляем величины (3) в уравнение (1) и подставляем величины (3) в уравнение (1) , откуда , откуда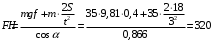 . .Ответ: 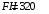 . . Задача 34Двухступенчатый стальной брус, длины ступеней которого указаны на рисунке - 4 (схемы 31-40) нагружен силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆l свободного конца бруса, приняв Е = 2 • 105 МПа. Проверить прочность бруса и указать, насколько (в процентах) брус недогружен или перегружен [σ] = 160 МПа. Исходные данные для своего варианта взять из таблицы - 5. Дано: 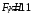 , , 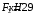 , , 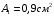 , , 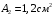 , схема 34 . , схема 34 .Найти:  . .  Решение Разбиваем брус на участки, как показано на рис.6а. Пользуясь методом сечений, определяем значения продольных сил 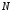 на участках бруса: на участках бруса: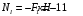 , , 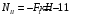 , ,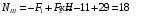 . .Строим эпюру продольных сил 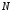 (рис.6б). (рис.6б).Вычисляем значения нормальных напряжений  : : , , , , . .Строим эпюру нормальных напряжений 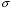 (рис.6в). (рис.6в).Из эпюры 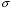 видно, что наиболее напряженными являются сечения бруса на III участке: видно, что наиболее напряженными являются сечения бруса на III участке: 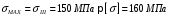 , т.е. брус недогружен. , т.е. брус недогружен.Степень недогрузки 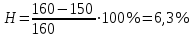 . .Определяем перемещение  свободного конца бруса. свободного конца бруса.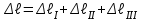 , ,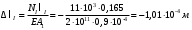 , , , ,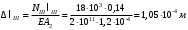 . .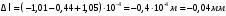 . .Ответ: 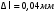 . Брус сжат. . Брус сжат.Задача 44Для двухопорной балки определить реакции опор (рисунок – 5, таблица – 6), построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение балки, составленное из двух швеллеров, если [σ] = 160 МПа. Дано: 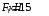 , , 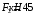 , ,  , схема 44. , схема 44.Найти: 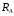 , , 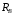 . .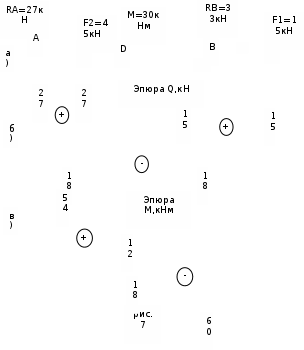 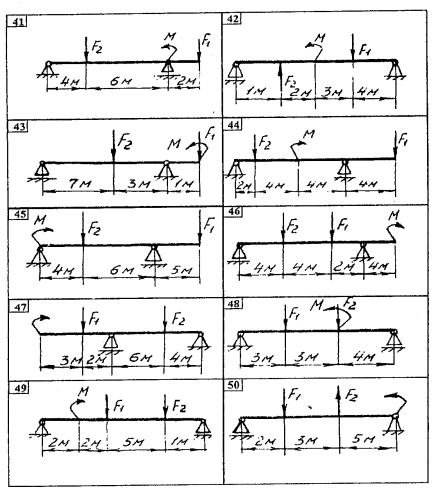 Решение Определяем опорные реакции балки из уравнения равновесия (рис.7а). 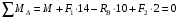 , , 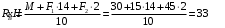 . .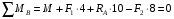 , ,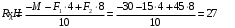 . .Проверка:  . .Разбиваем балку на участки по характерным точкам А, В, С,D, Е (рис.7а). Используя метод сечений, определяем значения поперечных сил 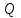 и изгибающих моментов и изгибающих моментов  в характерных точках балки. в характерных точках балки.Участок АС. Ход слева. 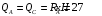 , , 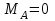 , , 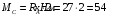 . .Участок СD. Ход слева. 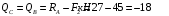 , , 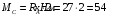 , , 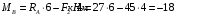 . .Участок EВ. Ход справа. 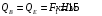 , ,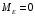 , , 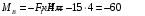 . .Участок ВD. Ход справа.  , ,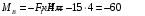 , , 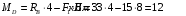 . .Строим эпюры 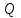 и и  (рис.7б,в). (рис.7б,в).Подбираем размеры поперечного сечения из условия прочности. Определим опасное сечение балки. Им будет сечение  , где изгибающий момент имеет наибольшее значение , где изгибающий момент имеет наибольшее значение  . .Подбор сечения из двух швеллеров производим из условия прочности по формуле:  , ,где 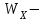 осевой момент сопротивления сечения. осевой момент сопротивления сечения.Для одного швеллера 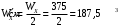 . .В соответствии с ГОСТ 8240-89 выбираем сечение из двух швеллеров №22 с 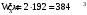 . .Проверяем прочность балки: 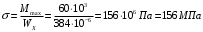 . .Степень недогрузки 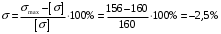 . .что находится в разрешенных пределах (менее 10%). Ответ: выбрано сечение из двух швеллеров №22. Задача 54Привод состоит из электродвигателя мощностью Рдв с частотой вращения nдв и двухступенчатой передачи, включающей редуктор и открытую передачу, характеристики звеньев которой (d или z заданы) . Дайте характеристику привода и его отдельных передач (рисунок – 6, таблица 7). Определите: а) общие КПД и передаточное отношение привода; б) мощности, угловые скорости и вращающие моменты для всех валов. Выполнить геометрический расчет передачи редуктора. Тип передачи (червячная, цилиндрическая прямо- или косозубая). При расчете цилиндрических передач принять следующие значения относительной ширины колеса φ = 0,4 для прямозубой передачи и 0,5 для косозубой. КПД передач смотрите в приложении. Дано: 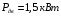 , , 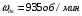 , , 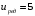 , , 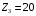 , ,  , , , ,  , схема 54. , схема 54.   Решение Рассмотрим кинематическую схему данного привода, дадим характеристику ему и передачам, входящим в него. Привод двухступенчатый, т.к. он состоит из двух передач. Все они понижающие, т.к. диаметр ведомой детали в каждой передаче больше диаметра ведущей детали. Первая ступень- передача зубчатая цилиндрическая прямозубая, закрытая (в корпусе – редуктор), она состоит из шестерни 1 (ведущая деталь) и колеса 2 (ведомая деталь). Вторая ступень-передача цепная, открытая, она состоит из ведущей звездочки 1, ведомой звездочки 2 и цепи, одетой на них. Привод имеет три вала- они обозначены на кинематической схеме римскими цифрами. КПД отдельных передач: η1-2 = 0,97 – закрытая зубчатая цилиндрическая передача; η3-4 = 0,92 –цепная передача. Общий КПД передачи 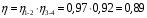 . .3. Мощности на валах: 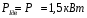 , ,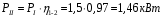 , ,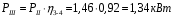 . .4. Передаточные числа отдельных передач:  , ,  . .Общее передаточное отношение передачи 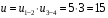 . .5. Угловые скорости валов:  , ,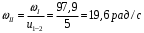 , ,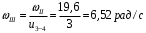 . .6. Вращающие моменты на валах:  , ,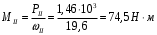 , ,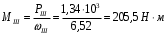 . .Выполняем геометрический расчет передачи редуктора. Определяем значение модуля закрытой цилиндрической прямозубой передачи из соотношения 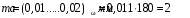 . .Определяем число зубьев шестерни Z1из формулы 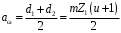 , ,  . .Принимаем 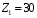 . .Определяем число зубьев колеса z2 , округляя полученное значение до ближайшего целого числа. Уточняем значение передаточного числа и. 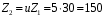 . .Принимаем 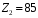 . .Определяем фактическое передаточное число передачи 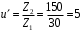 . .Отклонения от заданного 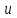 нет. нет.Определяем основные геометрические параметры зацепления: a) шаг 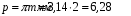 ; ;б)высота головки зуба 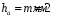 , , высота ножки зуба 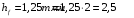 . .Определяем основные геометрические размеры колес: а) делительные диаметры  , , . .б) диаметры вершин зубьев  , , . .в) диаметры впадин  , ,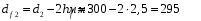 . .г) уточненное межосевое расстояние 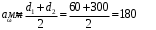 . .д) ширина зубчатого венца 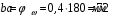 . .Принимаем 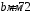 . .Список используемой литературы1. Аркуша А.И. Техническая механика: Теоретическая механика и сопротивление материалов. ― М.: Высшая школа, 2000. ― 352 с. 2. Аркуша А.И. Руководство к решению задач по теоретической механике. ― М.: Высшая школа 2002. ― 336 с. 3. Эрдеди А.А., Эрдеди Н.А. Детали машин. ― М.: Высшая школа Изд. Центр «Академия». 2001. ― 285 с. 4. Мовнин М. С., Израелит А. Б., Рубашкин А. Г. Основы технической механи-ки. Л., Машиностроение, 1990 5. Куклин Н. Г., Куклина Г. С. Детали машин. М., Высшая школа, 1987. |
