Контрольная работа (6 вариант). Задача 1. Определить величину и направление реакций связей для схемы, приведенной на рисунке 1
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
Контрольная работа (вариант 6) Задача №1. Определить величину и направление реакций связей для схемы, приведенной на рисунке 1. Исходные данные: α1 = 40° кН, α2 = 60°, G = 15 кН. 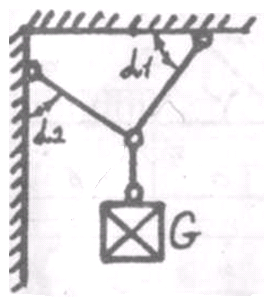 Рис. 1 Решение: Эта задача на равновесие плоской системы сходящихся сил. Для её решения необходимо выделить объект равновесия, т.е. тело или точку, где пересекаются линии действия всех сил. В нашем случае следует рассмотреть равновесие в точке В (рис. 2). По условию задачи к данной точке прикладываем силу G, с которой груз воздействует на объект равновесия, заменяя ее связь. Действие стержней АВ и СВ заменяем их реакциями, и также прикладываем к точке В. 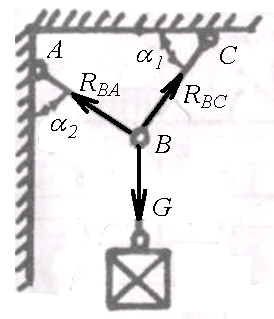 Рис. 2 Освободившись от связей, переносим данные силы на координатную плоскость так, чтобы точка равновесия находилась в начале осей координат, и составляем уравнение равновесия плоской системы сходящихся сил относительно оси x и y через проекции её слагаемых на каждую из двух координатных осей (рис. 3). 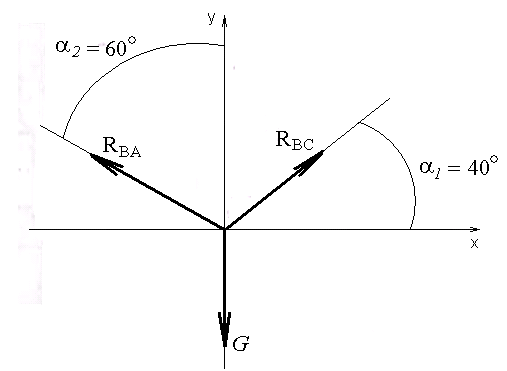 Рис. 3 Учитывая направление сил и угол наклона к каждой оси, составим уравнения проекций сил через уравнения равновесия плоской системы сходящихся сил: ΣFx = 0 => RВС·cos40° – RВА·sin60° = 0 ΣFy = 0 => RВС·sin40° + RВА·cos60° – G = 0 Выражаем из первого уравнения реакцию стержня, например RВС, подставляем во второе уравнение и находим реакцию стержня RВА, затем найденное значение подставляем обратно в первое уравнение и находим реакцию RВС. RВС = RВА·sin60° / cos40° RВА·sin60°·sin40° / cos40° + RВА·cos60° – G = 0 RВА·(sin60°·sin40° + cos60°·cos40°)/ cos40° = G RВА = G·cos40° / (sin60°·sin40° + cos60°·cos40°) RВА = 15·0,766 / (0,866·0,643 + 0,5·0,766) = 12,2 кН RВС = 12,2·0,866 / 0,766 = 13,8 кН Усилия в стержнях АВ и СВ от приложенной внешней силы получились соответственно 12,2 кН и 13,8 кН. То, что найденные значения сил получились со знаком «+», говорит о том, что мы угадали их направления, так как реакции опор всегда направлены против действия нагрузки. Проверим правильность решения задачи графическим способом, откладывая векторы найденных сил в масштабе их значений один за другим. 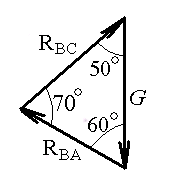 Условие выполняется, силы сошлись в точке, от которой мы начали откладывать векторы, расчет выполнен правильно. Задача №2. Определить опорные реакции балки с шарнирно-подвижной и шарнирно-неподвижной опорами. Схема задачи приведена на рисунке 4. Данные, необходимые для расчета приведены в таблице 1. 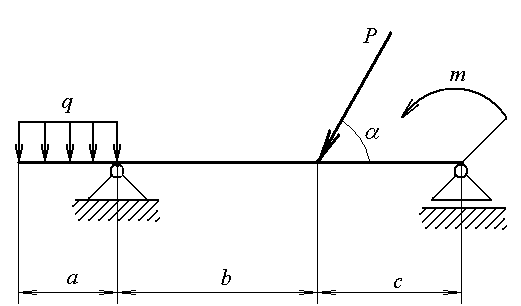 Рис.4 Таблица 1 – Исходные данные
Решение: В данной задаче будем рассматривать плоскую систему произвольно-расположенных сил. Любую систему произвольно-расположенных сил действующую на тело можно путем сложения привести к одной равнодействующей силе или одной паре сил. Для этого применим простой способ, основанный на теореме о параллельном переносе сил. Так как по условию задачи имеем одну шарнирно-подвижную опору и одну шарнирно-неподвижную, то на первую будет действовать одна реакция, а на вторую две реакции опоры. Условно покажем реакции опор, действующих на балку, на координатной плоскости (рис. 5), и составим систему уравнений сил относительно оси x и моментов сил относительно опор, исходя из условия, что изгибающий момент численно равен алгебраической сумме моментов сил по одну сторону от рассматриваемого сечения, где момент относительно точки равен произведению силы на плечо действия этой силы по отношению к заданной точке: Ми = Σ М0(Fi) 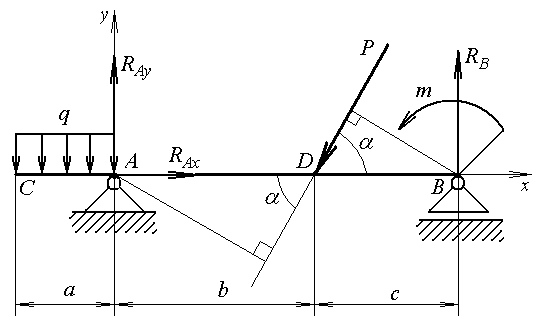 Рис. 5 Если момент пытается повернуть балку относительно выбранной точки по часовой стрелке, то он берется со знаком «+», в обратном случае — со знаком «–». ΣFx = 0 => RАх – Р·cosα = 0 ΣМА(Fi) = 0 => –m + Р·b·sinα – (b+c)·RВ – а·q·(а/2) = 0 ΣМВ(Fi) = 0 => –Р·с·sinα – m + (b+ c)·RАy – а·q·(b+ c+ (а/2)) = 0 Из каждого уравнения выражаем и определяем реакции опор. RАх = Р·cosα = 14·cos60º = 7 кН RВ = (–m + Р·b·sinα – а·q·(а/2)) / (b+ c) => RВ = (–8 + 14·2·sin60º – 1·6·(1/2)) / (2 + 1,5) = 3,78 кН RАy = (Р·с·sinα + m + а·q·(b+ c+ (а/2))) / (b+ c) => RАy = (14·1,5·sin60º + 8 + 1·6·(2+ 1,5+ (1/2))) / (2 + 1,5) = 14,34 кН Все полученные значения получились со знаком «+», значит выбранные нами направления сил правильные. В обратном же случае просто пришлось бы поменять направление сил, полученных со знаком «–», на противоположное. Теперь проведем проверку правильности решения по алгебраической сумме проекций всех внешних сил на ось перпендикулярную балке: ΣFy = 0 => RАy + RВ – а·q – Р·sinα = 0 14,34 + 3,78 – 1·6 – 14·sin60º = 0 14,34 + 3,78 – 6 – 12,12 = 0 0 = 0 Реакции опор определены правильно. Задача №3. Для заданной тонкой однородной пластины (рис. 6) определить положение центра тяжести. Размеры на чертеже даны в сантиметрах. 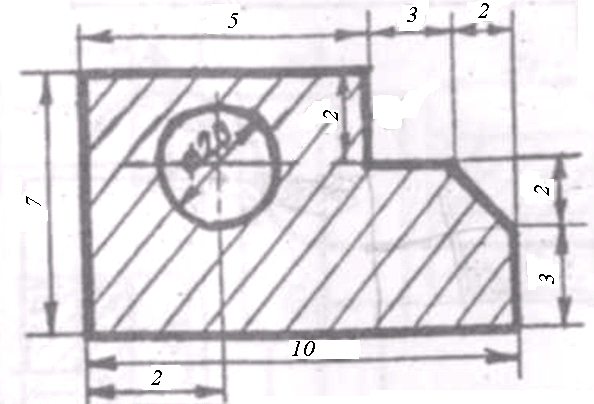 Рис. 6 Решение: Для определения центра тяжести сечения геометрической фигуры разобьем сложную фигуру на более простые и определим в каждой из этих фигур центр тяжести, чтобы впоследствии можно было воспользоваться формулой для нахождения координат центра тяжести составной фигуры: xc = Σ(Ai·xi) / Σ(Ai) yc = Σ(Ai·yi) / Σ(Ai) где Аi – площадь сечения, входящего в состав фигуры, см2. Разобьем фигуру так, как показано на рисунке 7 и проведем вспомогательные оси x0 и y0 для определения координат центров тяжести простейших геометрических фигур. 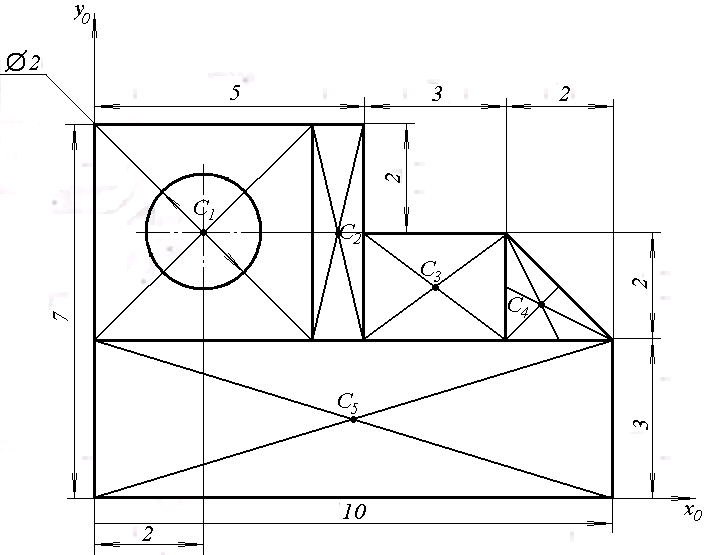 Рис. 7 Зная, что центр тяжести треугольника находится в точке пересечения его меридиан, а центр тяжести прямоугольника в точке пересечения его диагоналей, определим центр тяжести всех составных фигур. Не сложно определить, что координаты центров С1, С2, С3 и С5 будут равны: xC1 = 2 см, yC1 = 5 см; xC2 = 4,5 см, yC2 = 5 см; xC3 = 6,5 см, yC3 = 4 см; xC5 = 5 см, yC5 = 1,5 см; Для определения координат центра тяжести треугольника С4 воспользуемся формулой: xC4 = (xА4 + xB4 +xD4) / 3; yC4 = (yА4 + yB4 +yD4) / 3, где xА4, xB4,xD4, yА4, yB4,yD4 – координаты вершин треугольника (рис. 8). 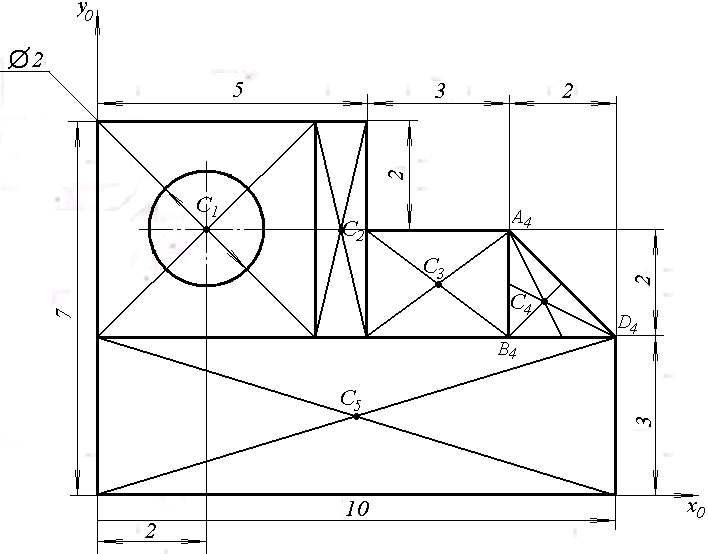 Рис. 8 Координаты вершин треугольников не сложно определить из рисунка: xА4 = 8 см, yА4 = 5 см; xB4 = 8 см, yB4 = 3 см; xD4 = 10 см, yD4 = 3 см. Теперь, зная координаты вершин треугольника, определяем координаты его центра тяжести: xC4 = (8 + 8 + 10) / 3 = 8,6 см, yC4 = (5 + 3 + 3) / 3 = 3,6 см. Осталось определить площади сечений составных фигур. Площадь первой фигуры, которая имеет форму квадрата, будет равна: А1 = 4 · 4 = 16 см2 Не забываем, что в этой фигуре вырезано отверстие радиусом 1 см. Определим площадь окружности: Аотв = π · R2 = 3,14 · 12 = 3,14 см2 Исходя из этого, площадь сечения первой фигуры будет равно: А1 = 16 – 3,14 = 12,86 см2 Площади прямоугольников будут соответственно равны: А2 = 1 · 4 = 4 см2 А3 = 3 · 2 = 6 см2 А5 = 10 · 3 = 30 см2 Площадь прямоугольного треугольника определим по формуле: А4 = ½ · h · а = ½ · 2 · 2 = 2 см2 Теперь зная координаты центров тяжести всех простейших сечений и их площади, определим координаты центра тяжести сечения заданной составной фигуры: xc = (A1·xС1 + A2·xС2 + A3·xС3 + A4·xС4 + A5·xС5) / (A1 + A2 + A3 + A4+ А5) xc = (12,86·2 + 4·4,5 + 6·6,5 + 2·8,6 + 30·5) / (12,86+4+6+2+30) = 4,55 см yc = (A1·yС1 + A2·yС2 + A3·yС3 + A4·yС4 + A5·yС5) / (A1 + A2 + A3 + A4 + А5) yc = (12,86·5 + 4·5 + 6·4 + 2·3,6 + 30·1,5) / (12,86+4+6+2+30) = 2,92 см Центр тяжести фигуры находится в точке С (xc; yc) = (4,55; 2,92) относительно вспомогательных координатных осей x0 и y0 и показан на рисунке 9. 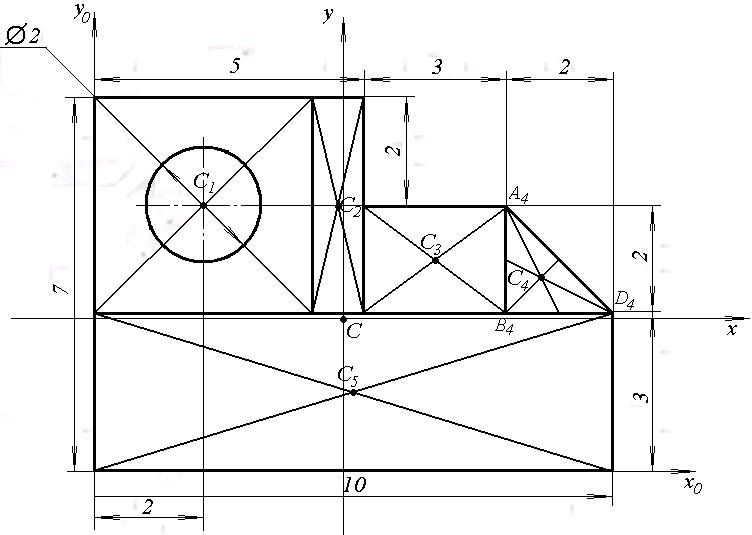 Рис. 9 Задача №6. Для заданного бруса (рис. 10) построить эпюру продольных сил, определить размеры поперечного сечения на обоих участках. Стержень выполнен из стали марки Ст 3, принять [σр] = 160МПа, [σсж] = 120МПа. Исходные данные: F1 = 5 кН, F2 = 12 кН. 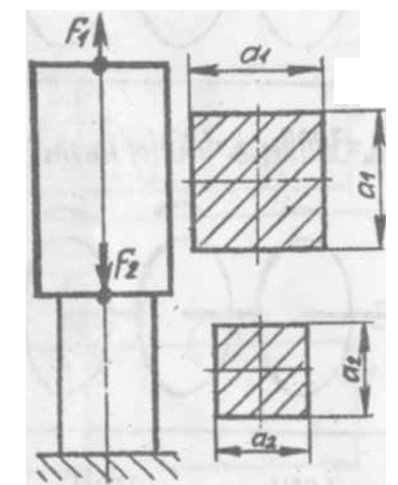 Рис. 10 Решение: Для построения эпюр продольных сил разбиваем рассматриваемое тело на участки, границами которых являются сечения, к которым приложены внешние нагрузки. 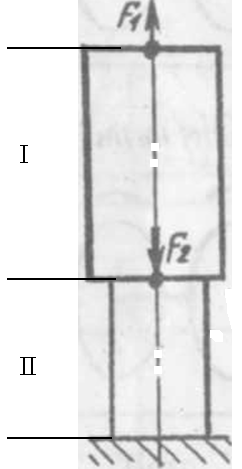 Рис. 11 Так как в нашем случае к брусу приложены две внешние нагрузки, то брус разобьется на два участка. Проведем расчет методом отсечения участков, начиная от свободного конца. Нагрузку, пытающуюся растянуть брус относительно заделки, будем принимать со знаком «+», а сжимающую брус — со знаком «–». Определим продольные силы: N1 = F1 = 5 кН, N2 = F1 – F2 = 5 – 12 = –7 кН Знак минус продольной силы означает, что брус на данном участке испытывает сжатие, т.е. в данном случае на первом участке происходит растяжение, а на втором — сжатие. По полученным данным построим эпюру продольных сил. Для этого относительно базовой линии откладываем полученные значения, учитывая знак (рис. 12). 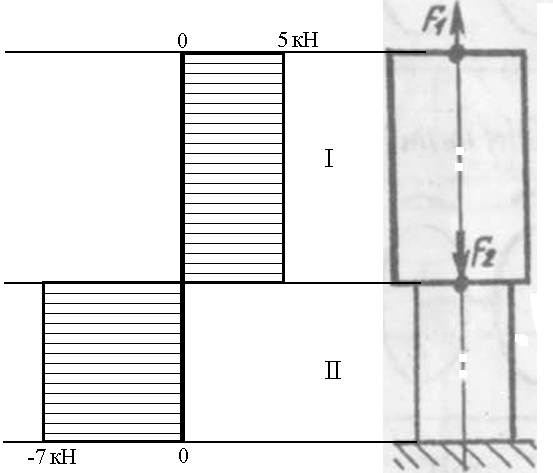 Рис. 12 Из условия прочности при растяжении и сжатии определим размеры поперечного сечения на обоих участках бруса. [σ] ≥ N / A, где N – расчетное нормальное напряжение по длине бруса, кН; А – площадь поперечного сечения участка бруса, мм2. Исходя из условия задачи, что нормальное напряжение на участке, где брус испытывает растяжение, равно [σр] = 160МПа, определим размеры поперечного сечения первого участка: [σр] ≥ N1 / A1 A1 ≥ |N1| / [σр] = |5 · 103| / 160 = 31,25 мм2 Зная, что поперечное сечение бруса квадратной формы, не сложно определить его требуемые размеры по найденной площади: а1 = √A1 = √31,25 = 5,6 мм Далее определим размеры поперечного сечения второго участка, учитывая, что нормальное напряжение на этом участке равно [σсж] = 120МПа: [σсж] ≥ N2 / A2 A2 ≥ |N2| / [σсж] = |–7 · 103| / 120 = 58,33 мм2 Определяем его требуемые размеры по найденной площади, исходя из того, что поперечное сечение бруса имеет квадратную форму: а2 = √A2 = √58,33 = 7,65 мм В результате получили минимальные предельно-допустимые размеры поперечного сечения на обоих участках бруса: а1 = 5,6 мм, а2 = 7,65 мм. Задача №7. На стальном валу круглого сплошного сечения насажены четыре шкива (рис. 13). Ведущий шкив, получая от двигателя вращающий момент m0, предает станкам через остальные шкивы вращающие моменты m1, m2, m3. Определить величину m0, исходя из условия равномерного вращения вала, а также построить эпюру крутящих моментов, определить диаметр на каждом участке вала. Для материала вала принять [τ] = 70 МПа. Исходные данные: m1 = 300 Н·м, m2 = 400 Н·м, m3 = 220 Н·м. 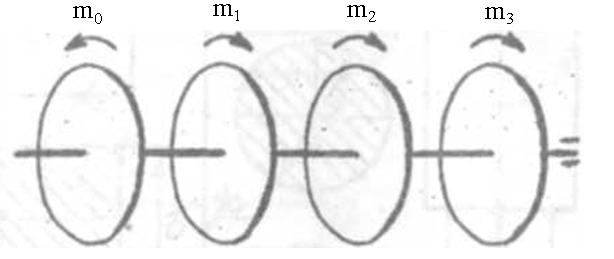 Рис. 13 Решение: Из условия задачи знаем, что вал находится в равновесии (в состоянии покоя или равномерного вращения), а значит алгебраическая сумма внешних моментов, приложенных к валу, равна нулю. Учитывая правило знаков по методу сечения запишем уравнение: m3 + m2 + m1 – m0 = 0 Отсюда определяем m0: m0 = m1 + m2 + m3 m0 = 300 + 400 + 220 = 920 Н·м Для построения эпюры крутящих моментов делим вал на участки, начиная со свободного конца, границами которых являются сечения, в которых приложены внешние скручивающие моменты, т.е. сечения, где насажены шкивы. 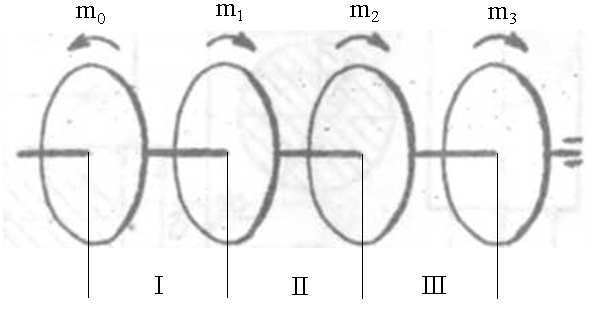 Рис. 14 Теперь, применяя метод сечения, определяем величину внутренних крутящих моментов в сечениях на каждом из участков бруса, начиная с первого. МкIслева = 0; МкIсправа = m0 = 920 Н·м; МкII = m0 – m1 = 920 – 300 = 620 Н·м; МкIIIслева = m0 – m1 – m2 = 920 – 300 – 400 = 220 Н·м; МкIIIсправа = m0 – m1 – m2 – m3 = 920 – 300 – 400 – 220 = 0. По найденным значениям строим эпюру крутящих моментов относительно базовой оси (рис. 15). 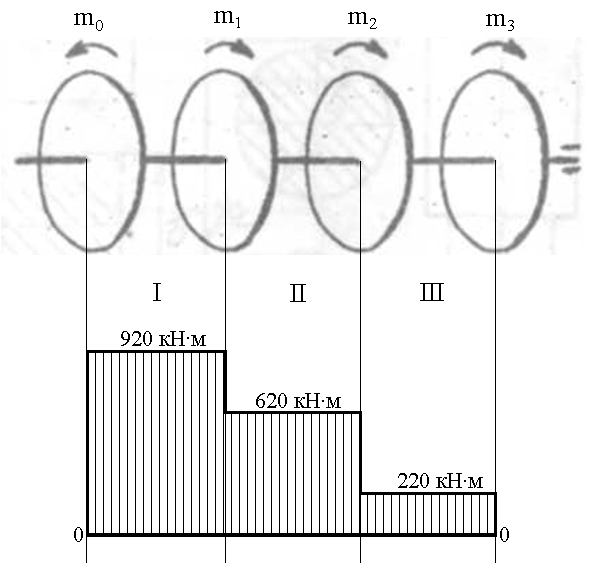 Рис. 15 Определим диаметр на каждом участке вала, используя условие прочности при кручении: [τ] ≥ τ = Мк / Wp, где Wp – полярный момент сопротивления, мм3. Для определения допустимого диаметра вала полярный момент сопротивления вала WP должен удовлетворять условию: WP ≥ Мк / [τ] По условию задачи для [τ] = 70 МПа = 70 Н·мм2 определим требуемый Wp для первого участка вала: WP(I) = МкI / [τ] = 920 · 103 / 70 = 13,14·103 мм3 Выражая полярный момент сопротивления через диаметр вала: WP = 0,2 · d3, находим его значение: d1 = 3√(WP(I)/0,2) = 3√(13,14·103/0,2) ≈ 40 мм Аналогично определяем диаметр вала на втором и третьем участке. Определяем требуемый Wp для второго участка вала: WP(II) = МкII / [τ] = 620 · 103 / 70 = 8,85·103 мм3 Выражаем диаметр вала через полярный момент сопротивления: d2 = 3√(WP(II)/0,2) = 3√(8,85·103/0,2) ≈ 35 мм Определяем требуемый Wp для третьего участка вала: WP(III) = МкIII / [τ] = 220 · 103 / 70 = 3,14·103 мм3 Определяем диаметр вала на третьем участке: d3 = 3√(WP(III)/0,2) = 3√(3,14·103/0,2) ≈ 25 мм Задача №8. Для заданной двухопорной балки (рис. 16) построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения. Для материала балки (сталь Ст 3) с учетом повышенных требований к ее жесткости принять σadm = 130 МПа. Исходные данные приведены в таблице 2. 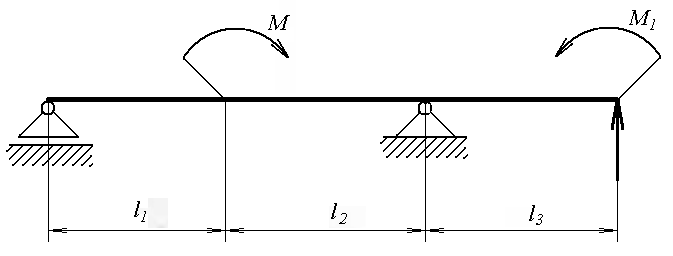 Рис. 16 Таблица 2 – Исходные данные
Решение: Изгиб прямых брусьев вызывается парами сил или силами перпендикулярными к его продольной оси. При таком виде деформации в поперечном сечении тела (балки) возникают два внутренних силовых фактора: поперечная сила QX и изгибающий момент Ми. Поперечная сила равна алгебраической сумме внешних сил, действующих по одну сторону от рассматриваемого сечения: Qy = ΣFi Изгибающий момент численно равен алгебраической сумме моментов сил по одну сторону от рассматриваемого сечения: Ми = Σ М0(Fi) Для построения эпюр сначала необходимо определить реакции опор балки. Так как по условию задачи имеем одну шарнирно-подвижную опору и одну шарнирно-неподвижную, то на первую будет действовать одна реакция, а на вторую две реакции опоры. Условно покажем реакции опор, действующих на балку, на координатной плоскости (рис. 17), и составим систему уравнений сил относительно оси x и моментов сил относительно опор: ΣFх = 0 => RВх = 0 ΣМА(Fi) = 0 => –0,1·RВy – 0,15·F + M – М1 = 0 => ΣМВ(Fi) = 0 => 0,1·RА – 0,05·F + M – М1 = 0 => Отсюда находим реакции опор: RВy = –0,15·F + M – М1 / 0,1 = –0,15·80 + 4 – 1 / 0,1 = –90 Н RА = 0,05·F – M + М1 / 0,1 = 0,05·80 – 4 + 1 / 0,1 = 10 Н 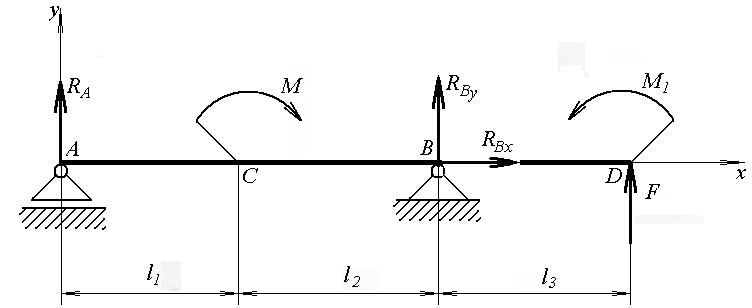 Рис. 17 Знак минус означает реакции RВy, что мы не угадали направление реакции опоры, т.е. сила в действительности направлена в обратную сторону. Проведем проверку по алгебраической сумме проекций всех внешних сил на ось перпендикулярную балке: RА + (–RВy) + F = 0 10 + (–90) + 80 = 0 0 = 0 Реакции опор определены правильно. В соответствии с местом приложения нагрузок — пары сил с моментом М и М1, реакций опор RА и RВy и сосредоточенной силы F разделим балку на три участка: I, II, III. Так как все участки балки свободны от распределенной нагрузки, то поперечные силы на каждом участке постоянны и эпюра Qy изобразится прямыми, параллельными базовой линии. Определим значения поперечных сил на каждом участке, применяя метод сечения. |
