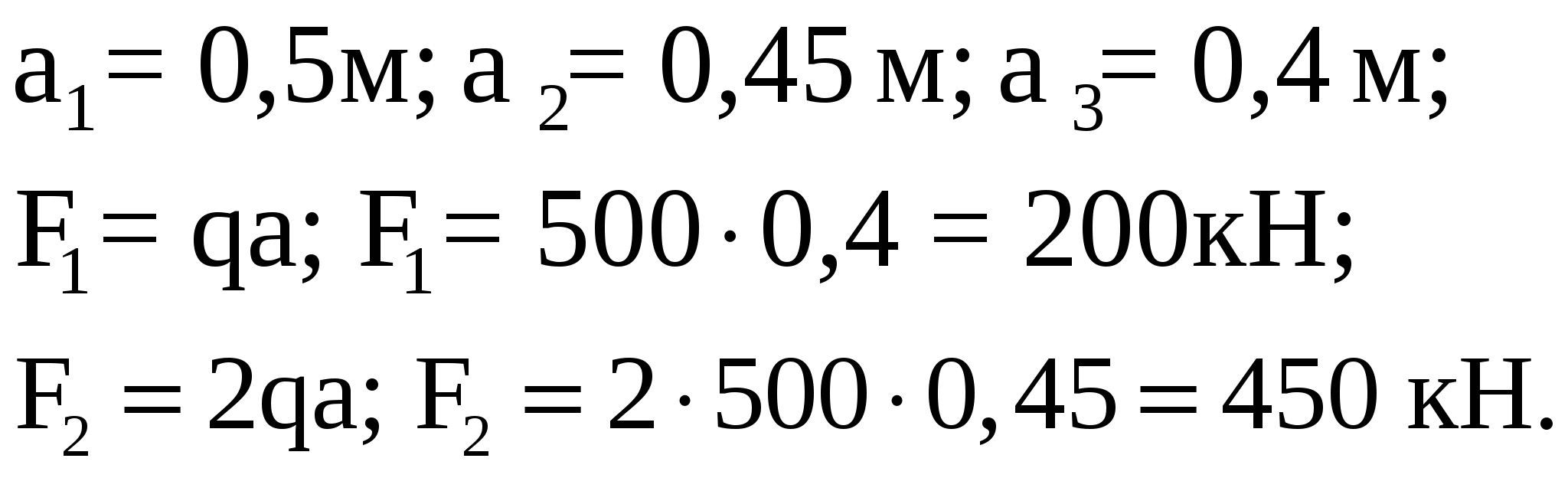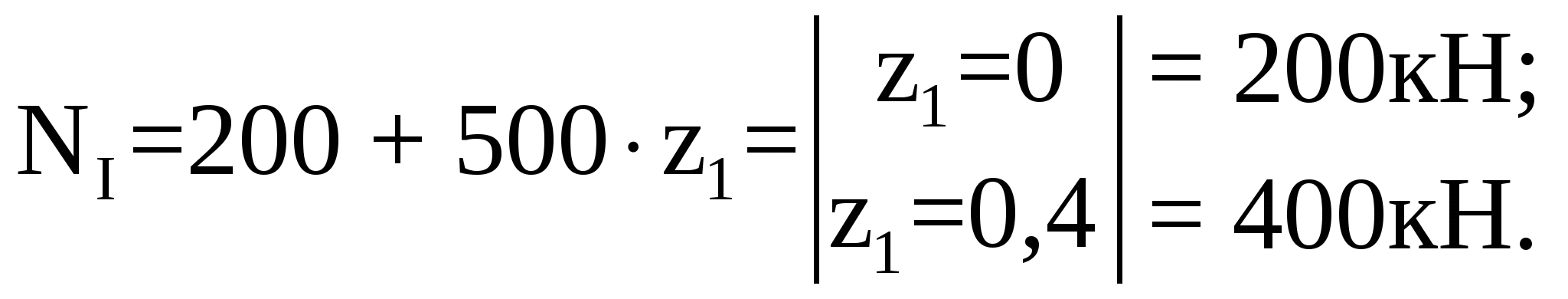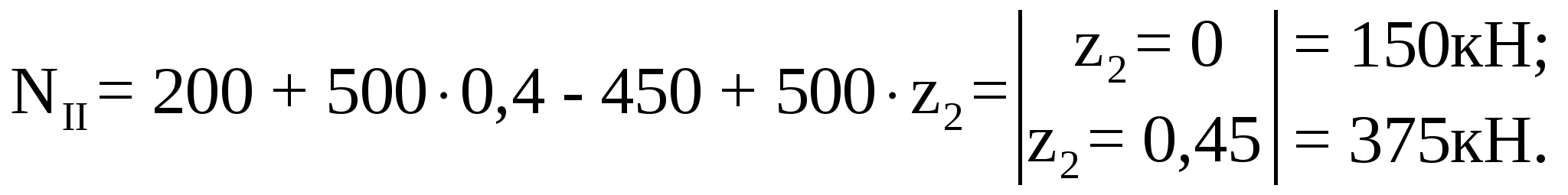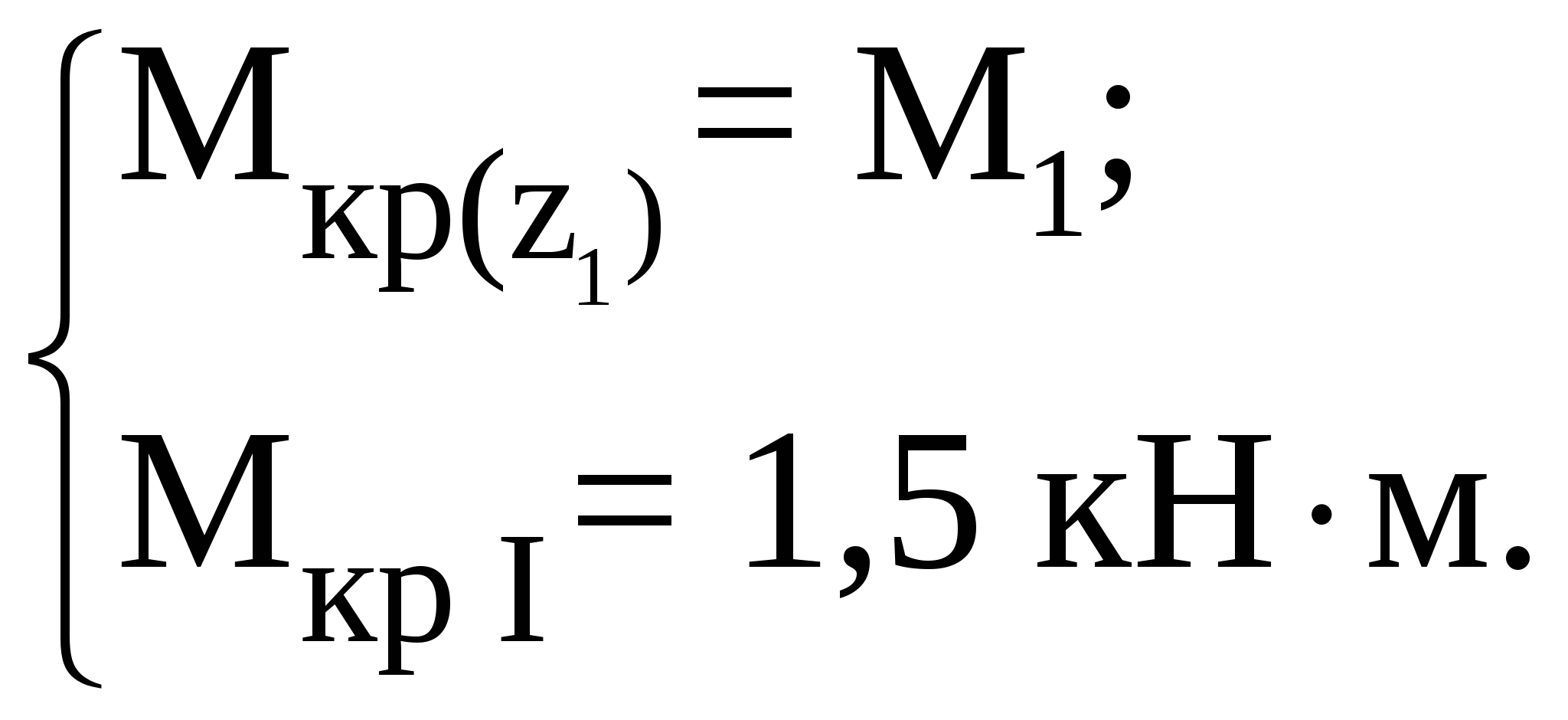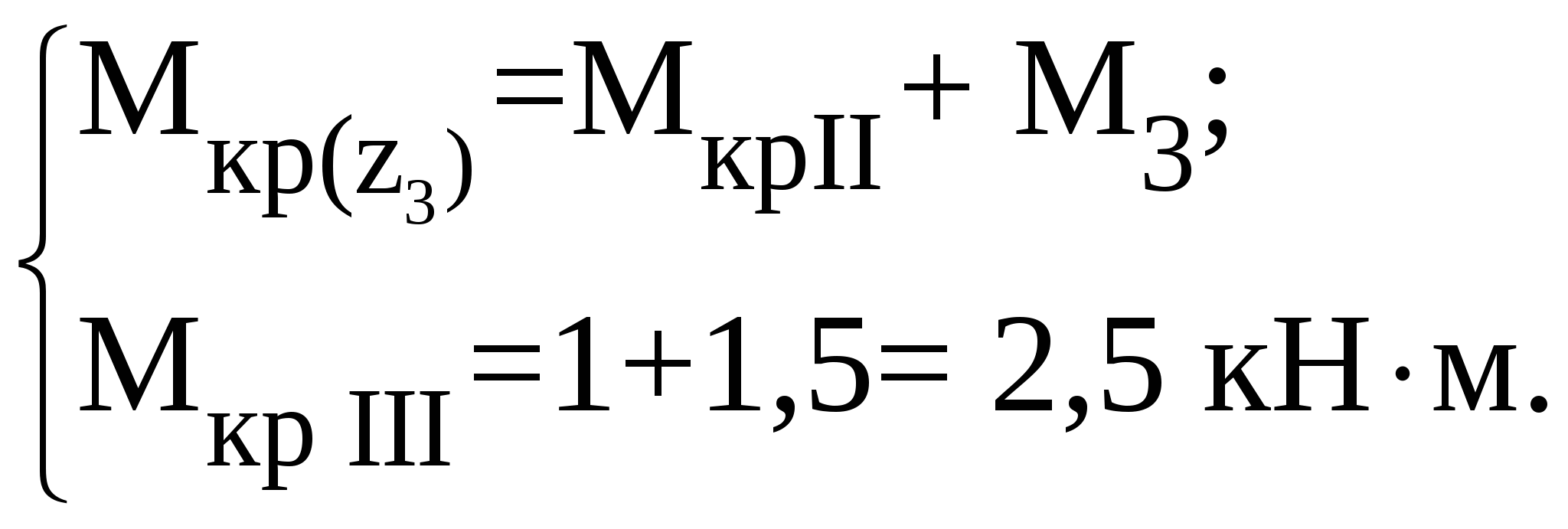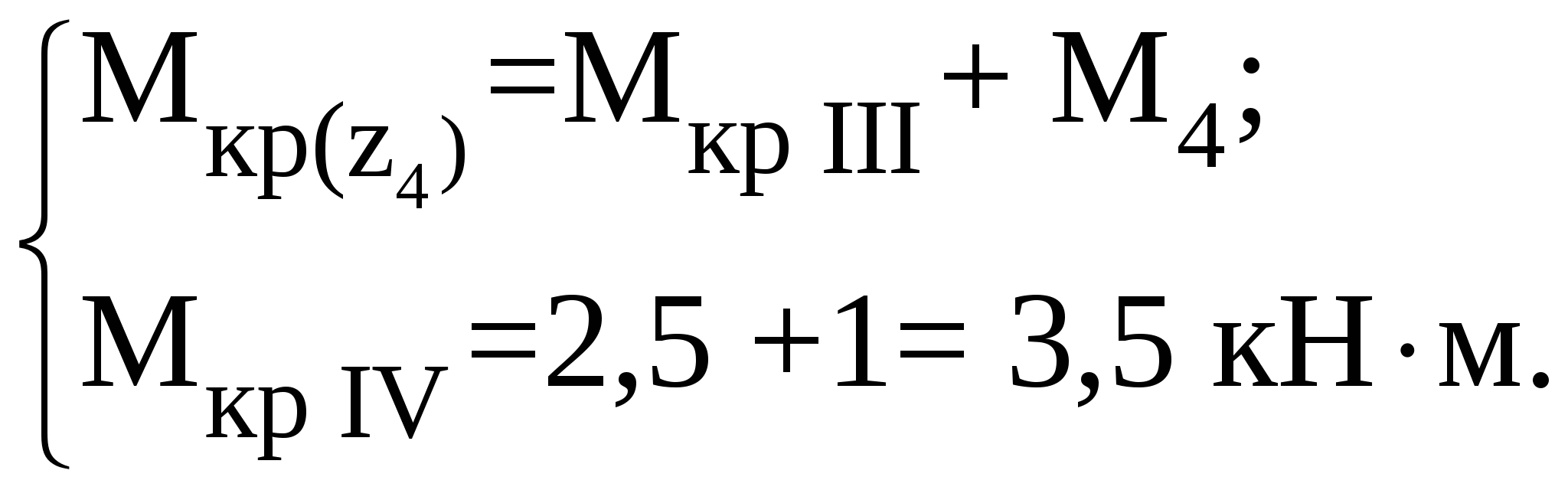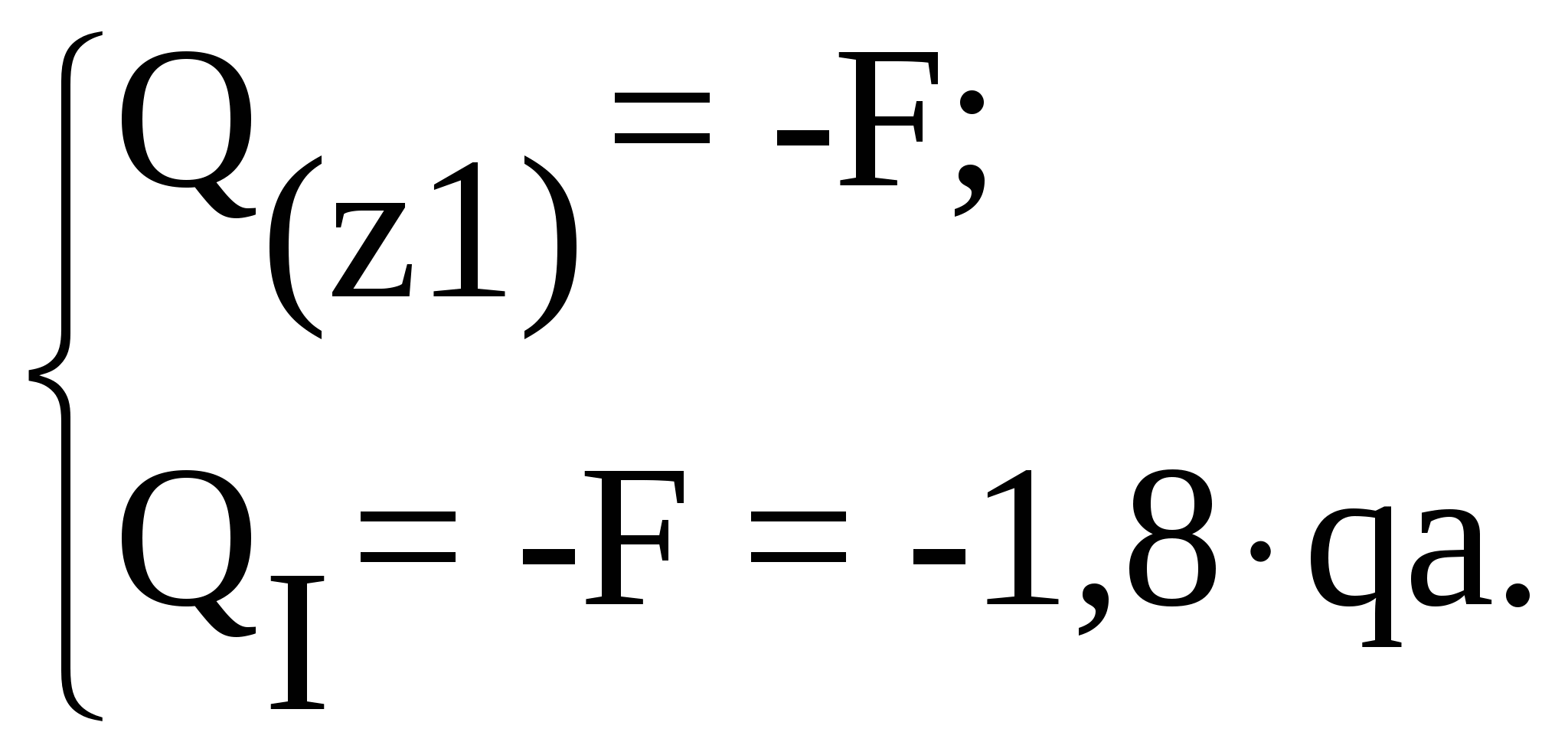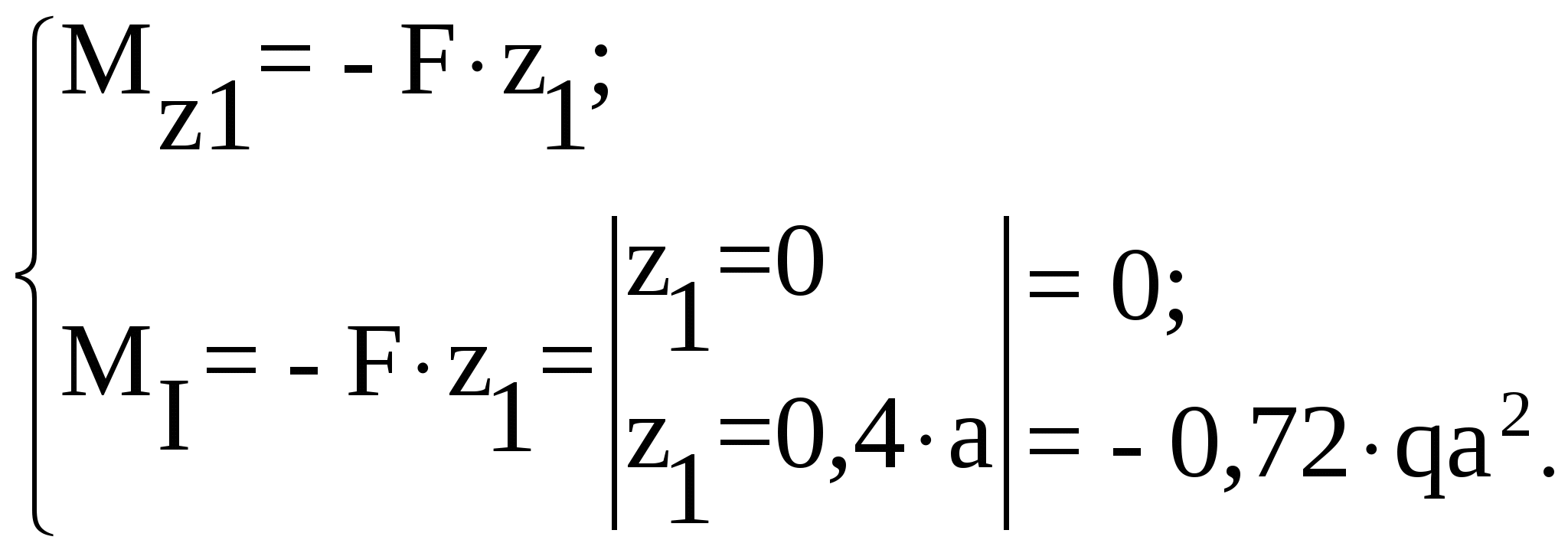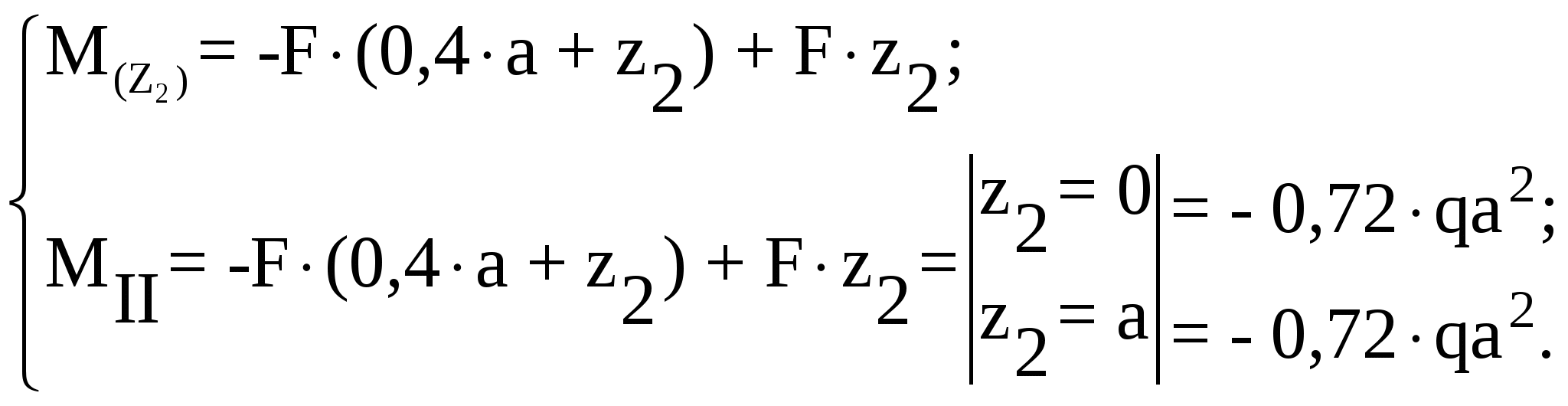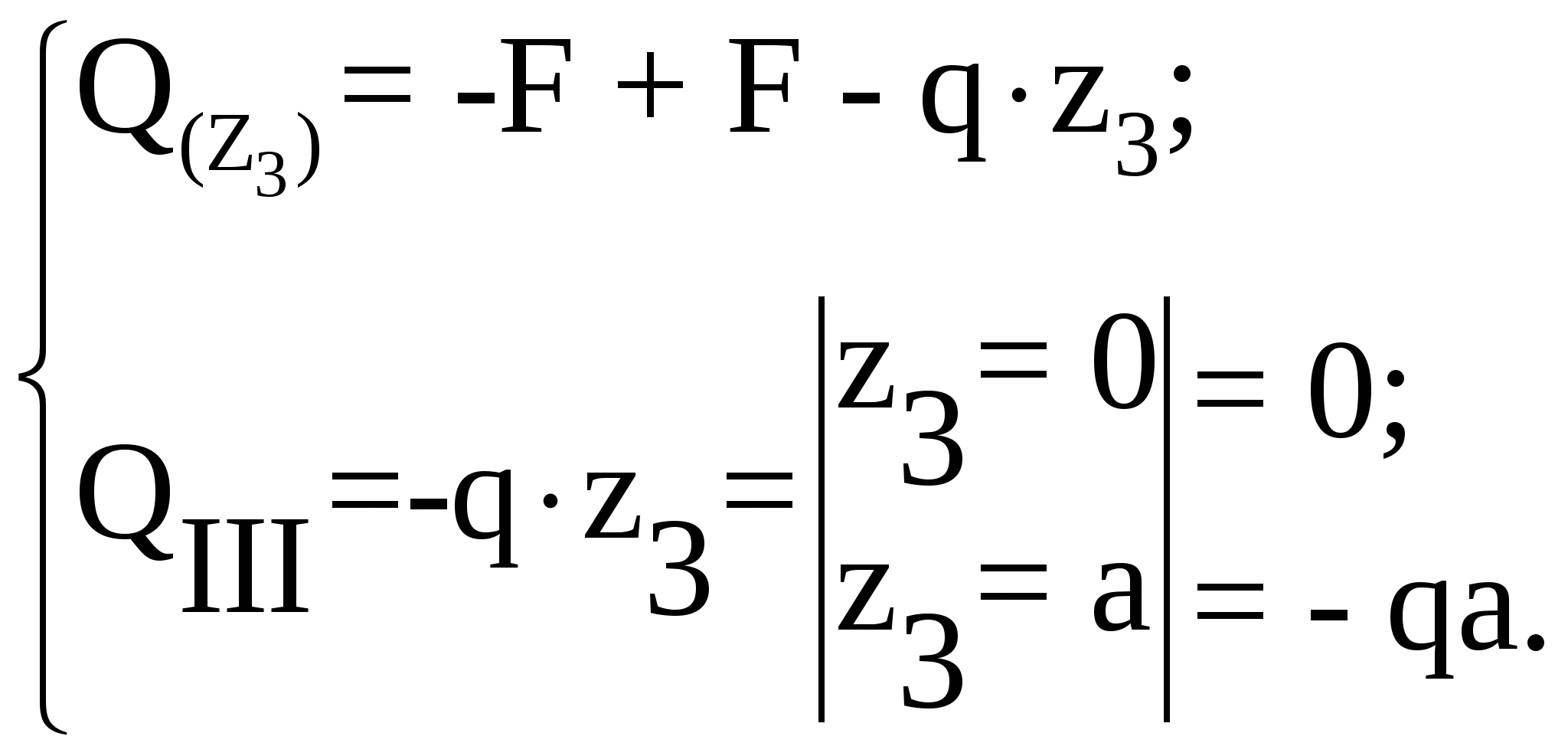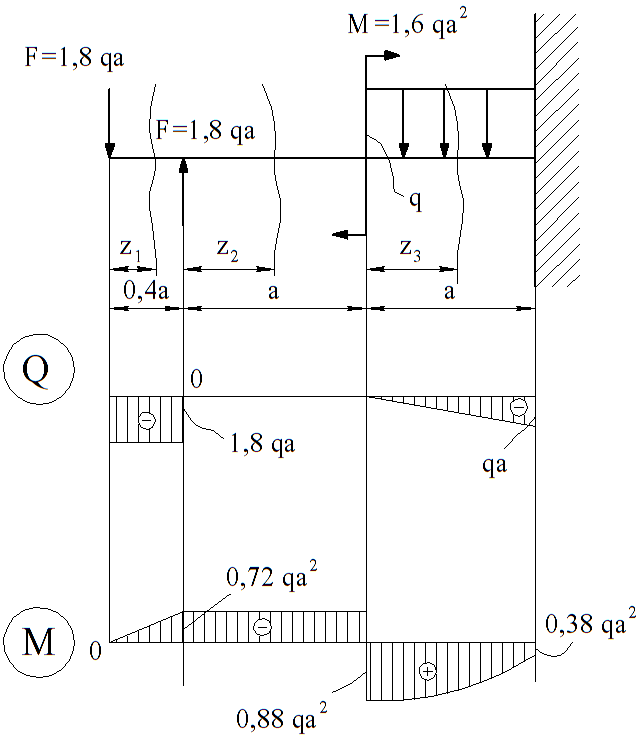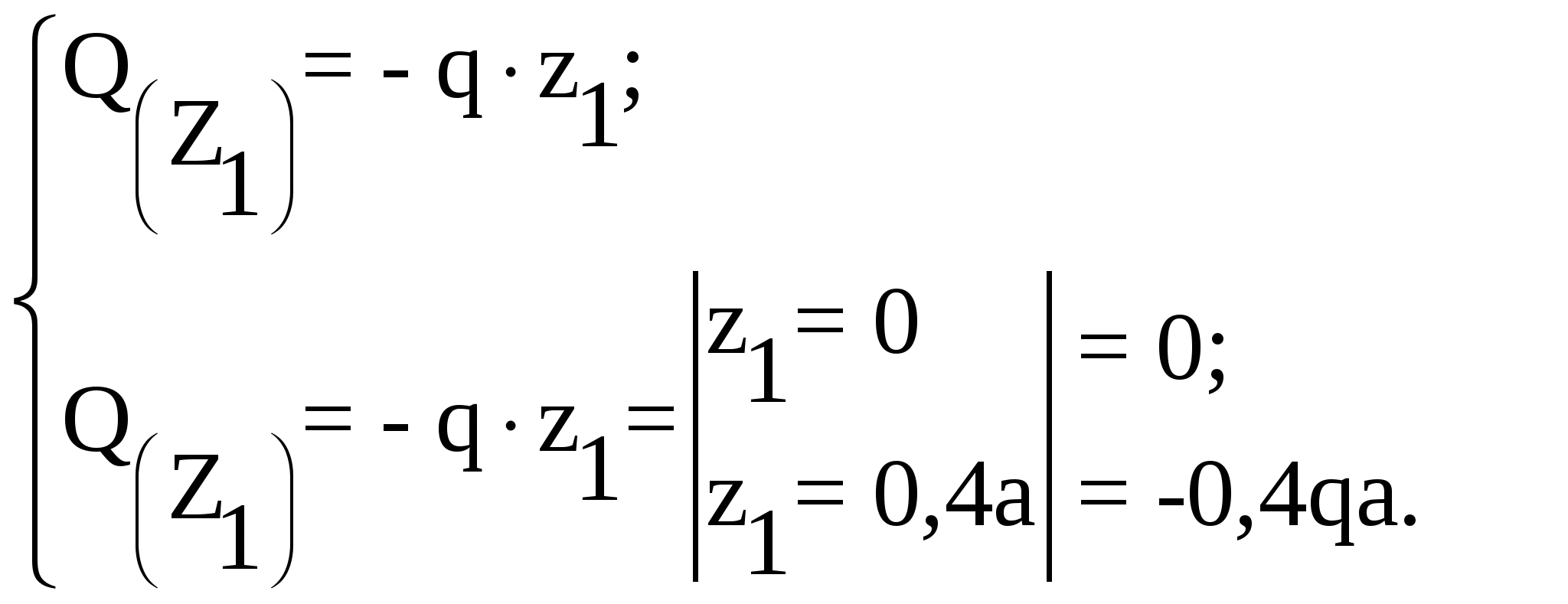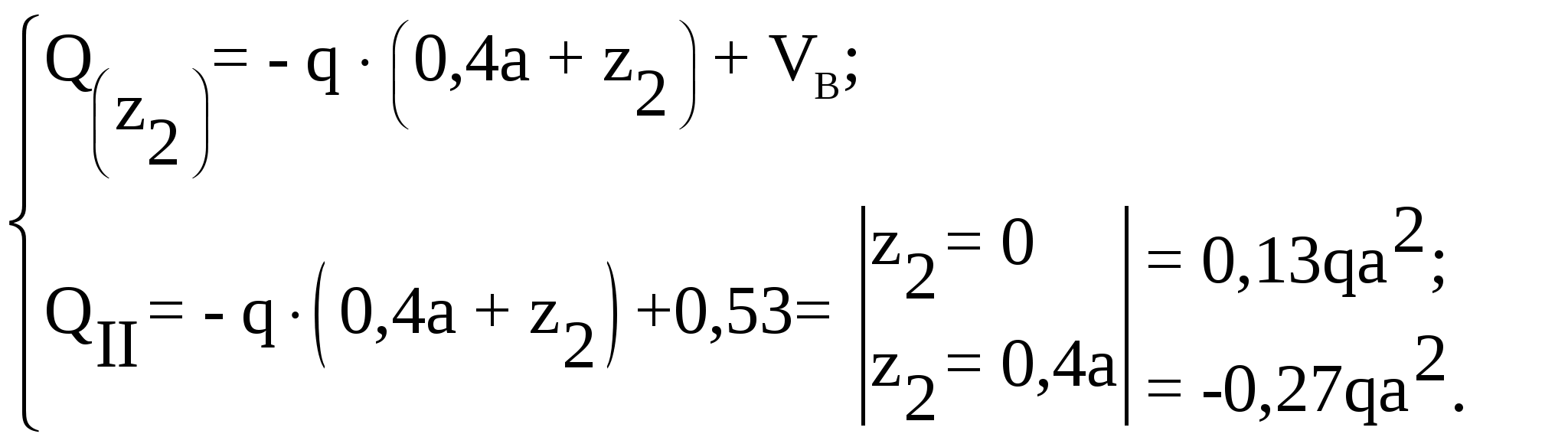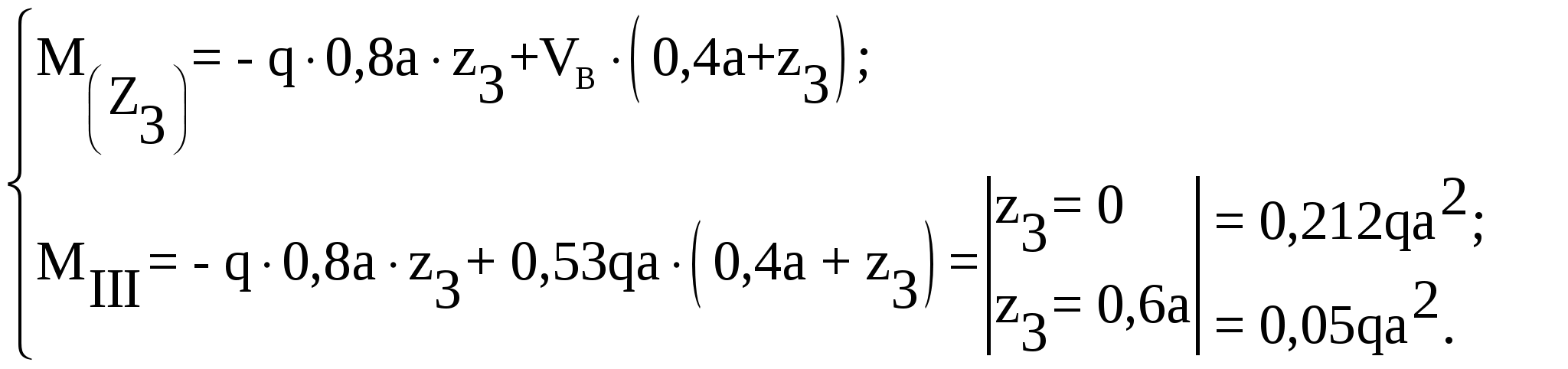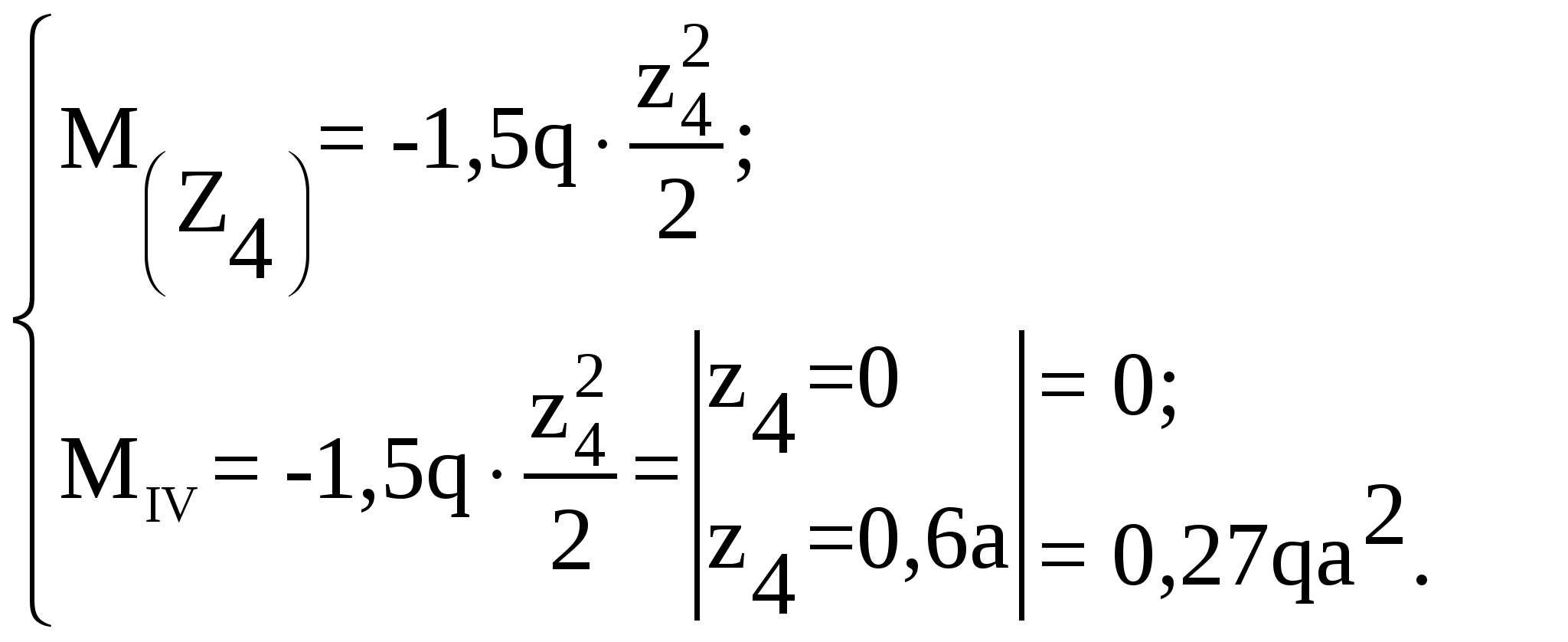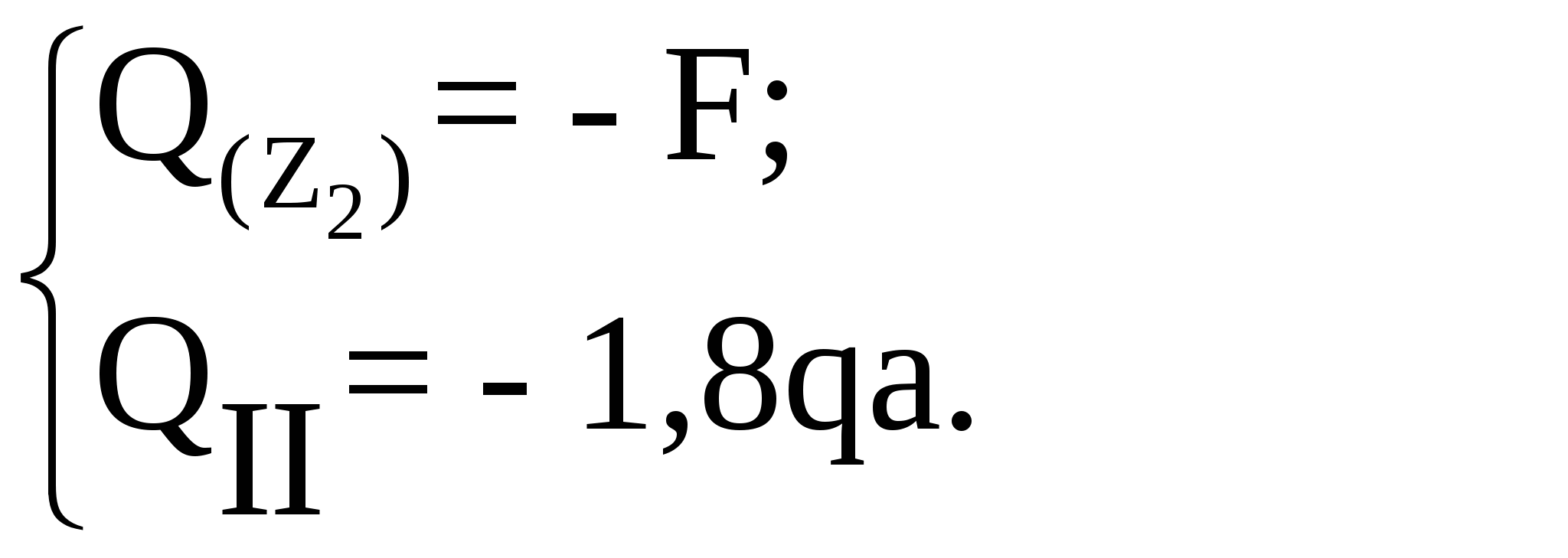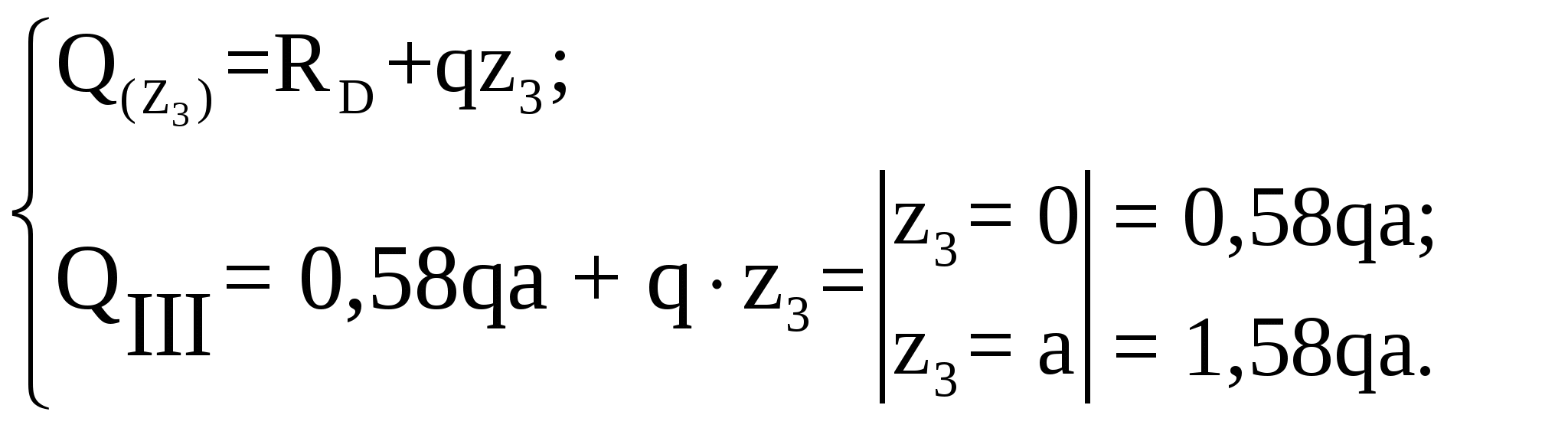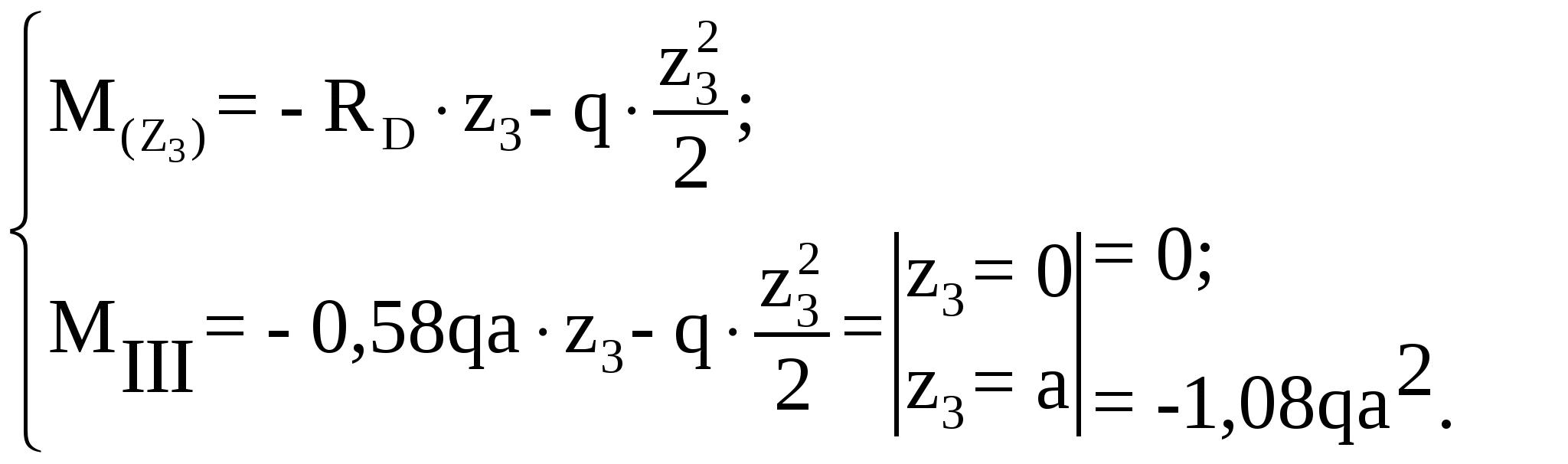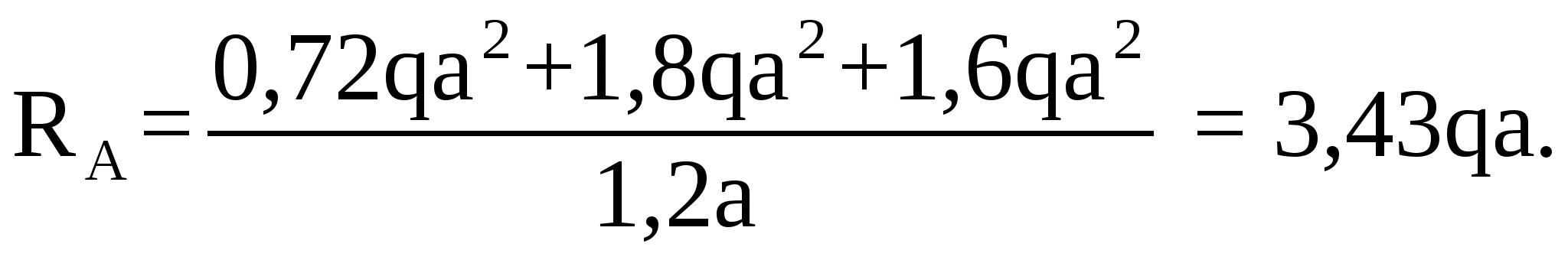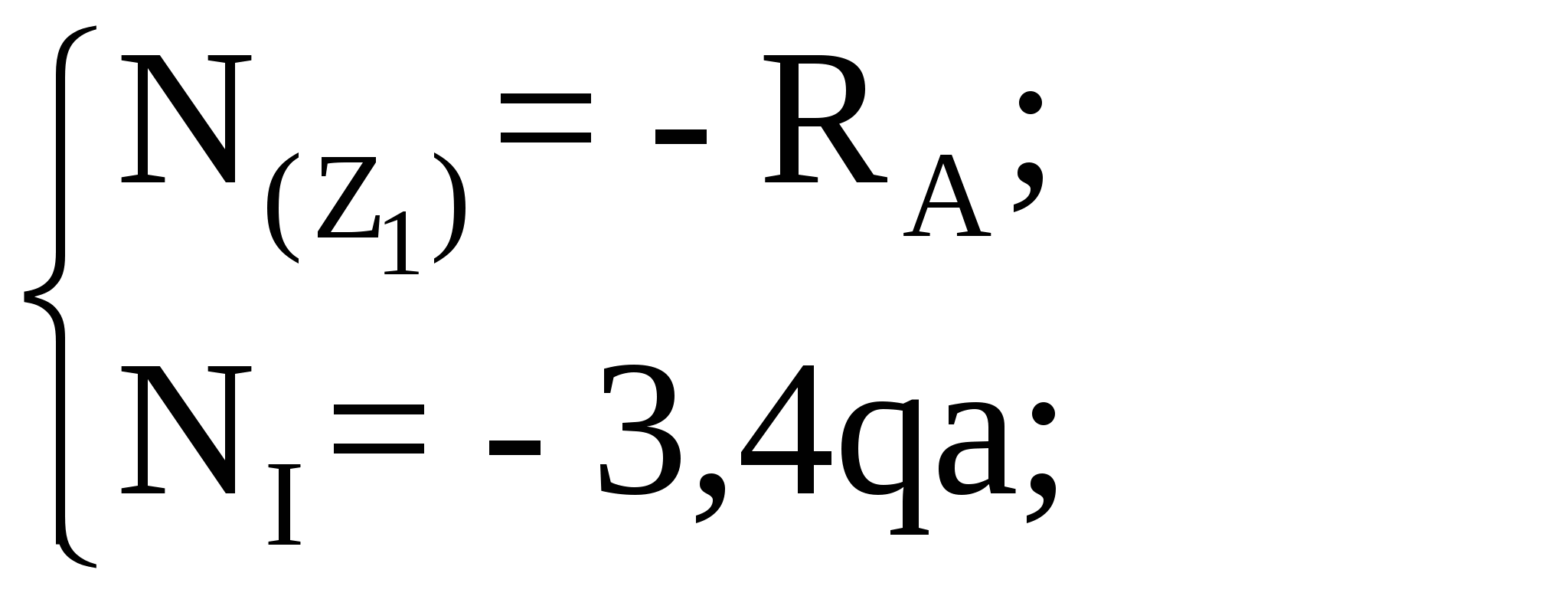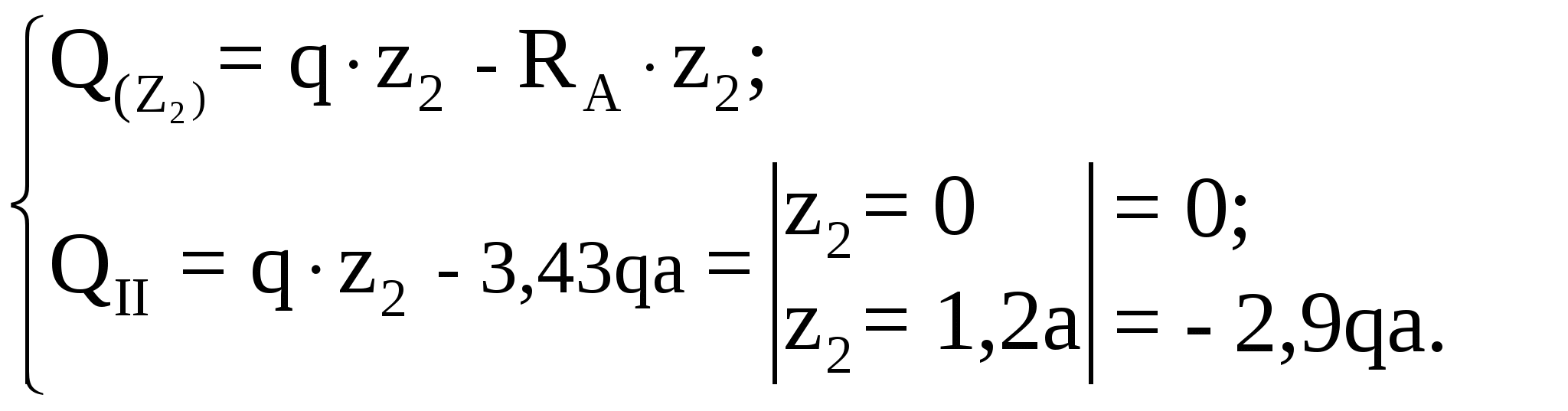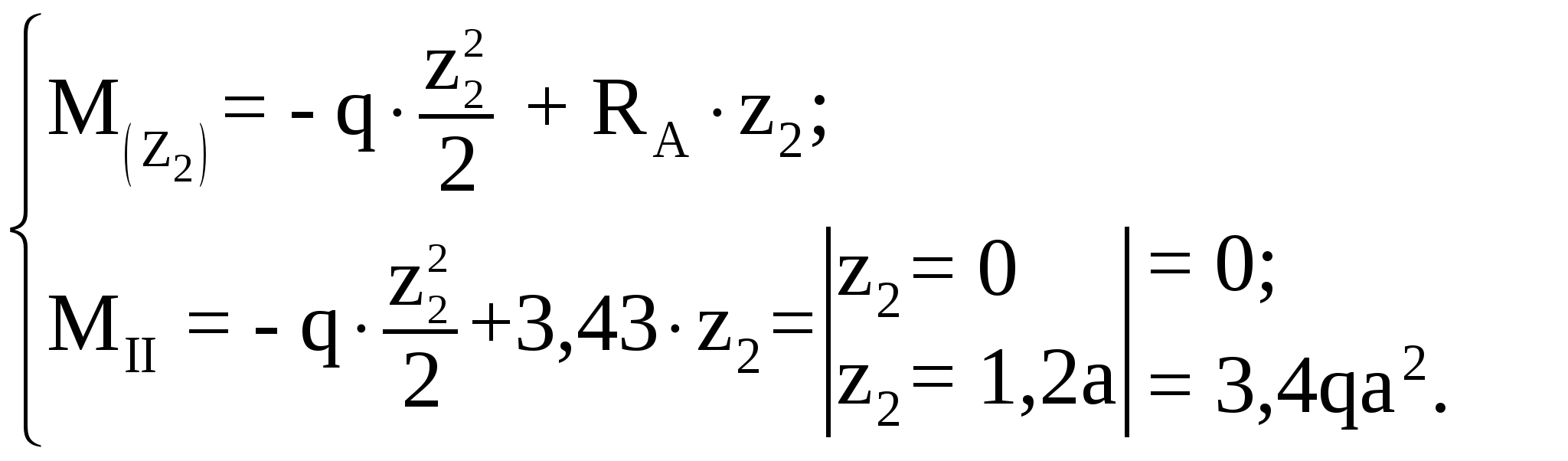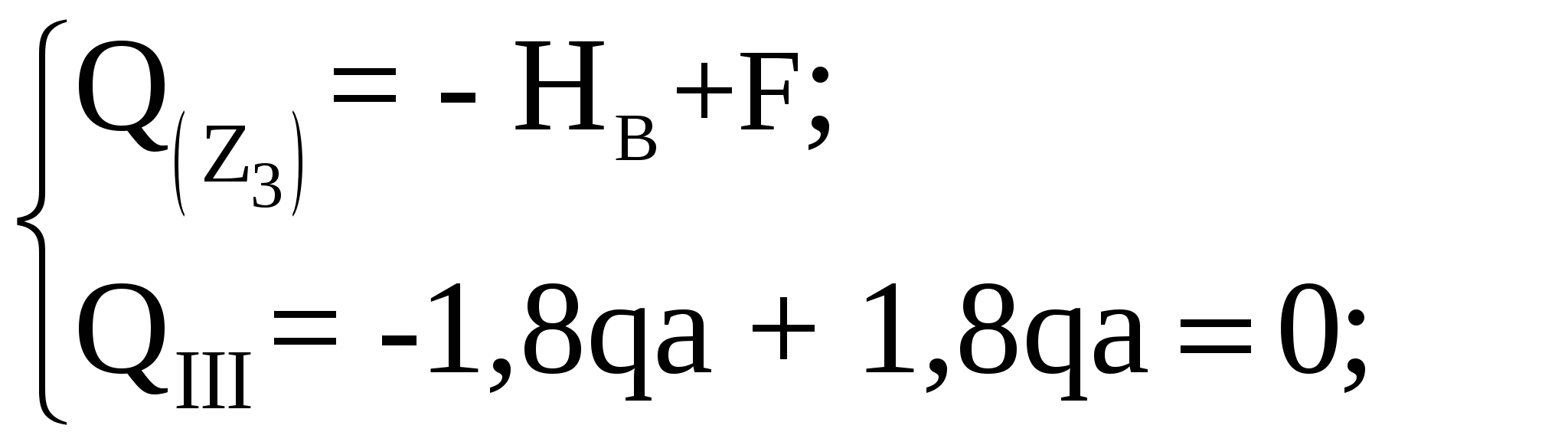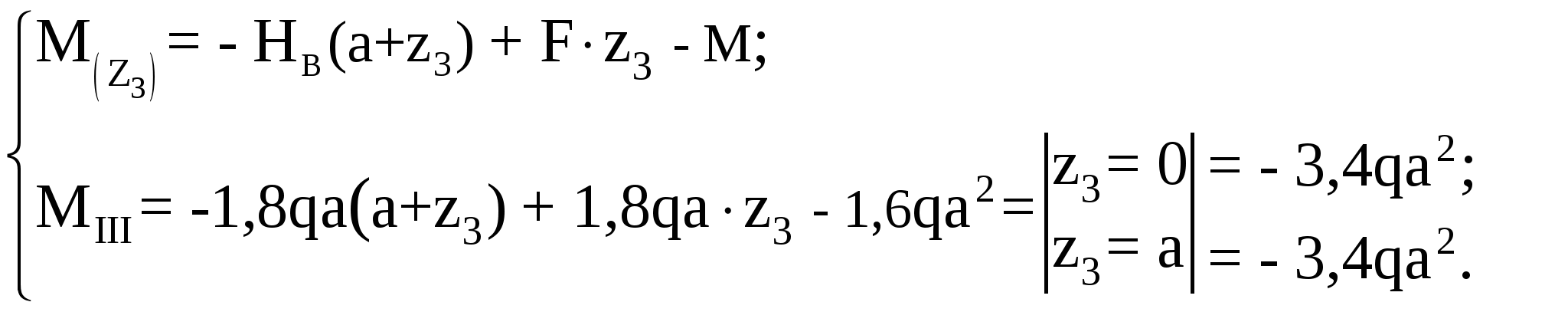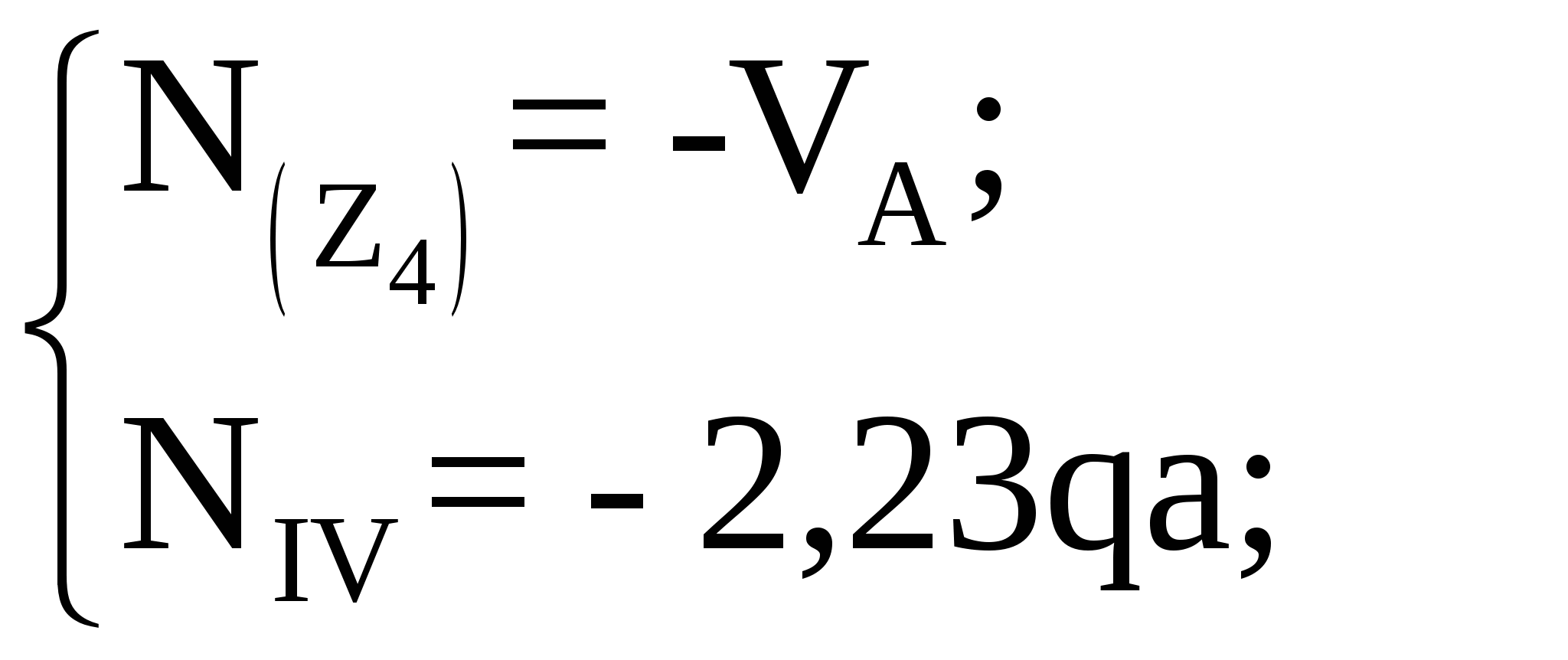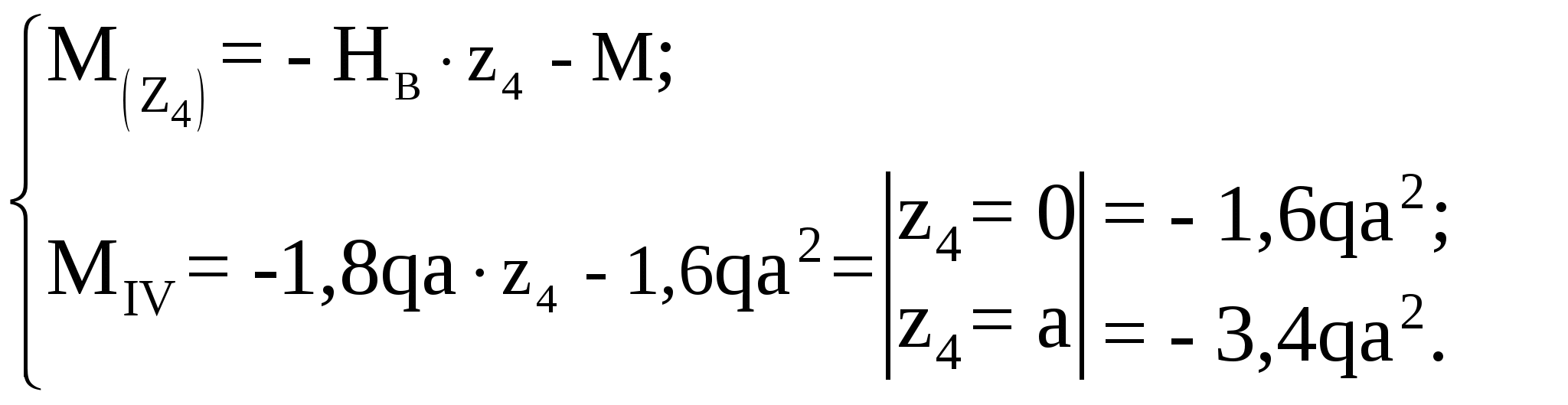Задача 1
Построение эпюры продольной силы
Исходные данные: 
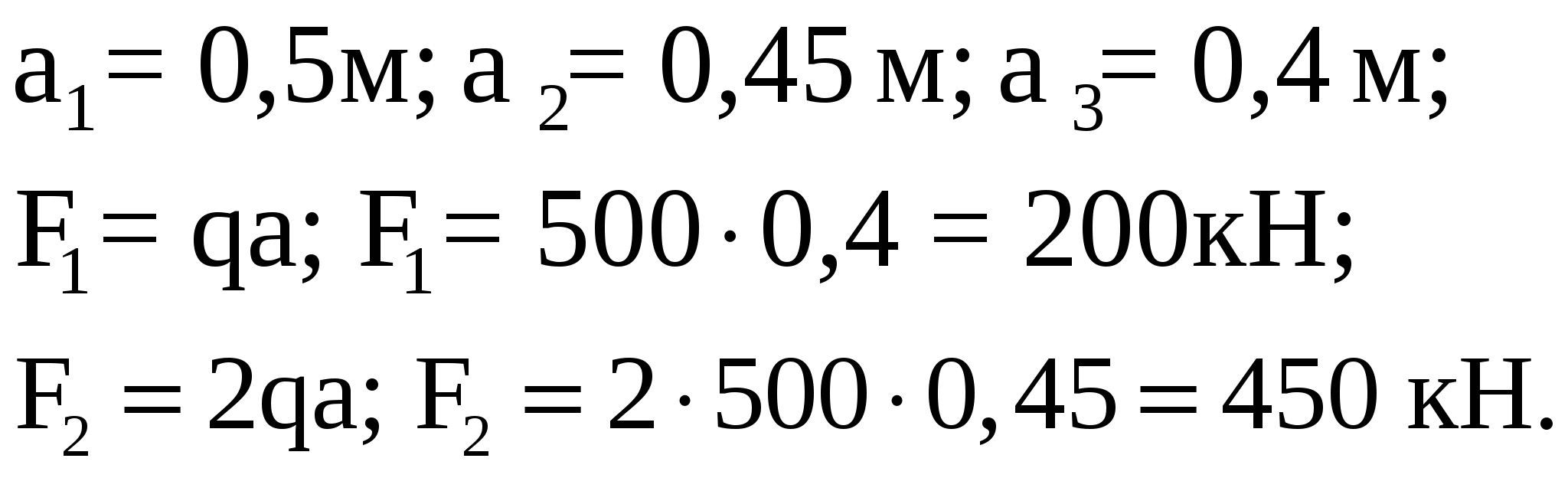
Заданная схема стержня представлена на рисунке 1.
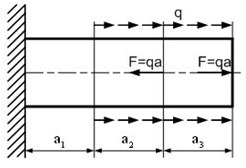
Рисунок 1.1 – Заданная схема стержня
Решение
Разбиваем стержень на три силовых участка AB, BC и CD (рисунок 1), для каждого участка применяем метод сечений и составляем уравнения продольной силы, по которым определяем ее характерные ординаты.
Рассмотрим участок I (АВ): 
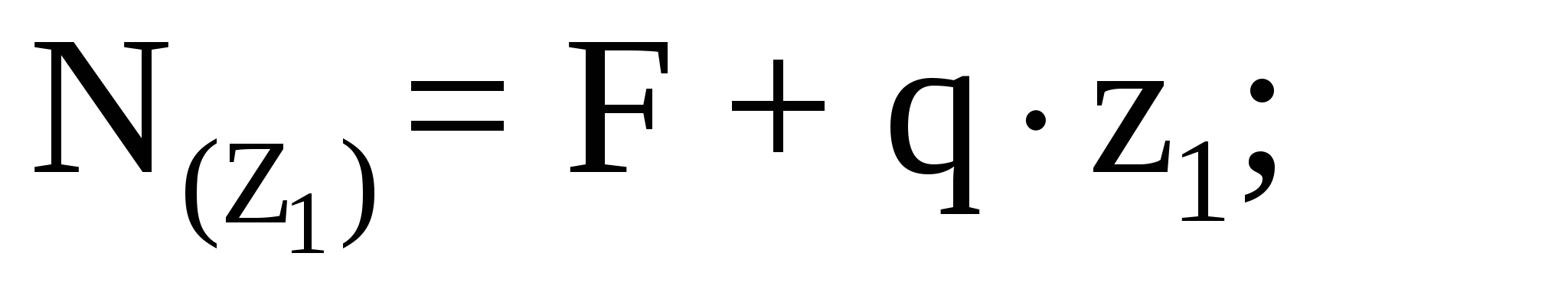
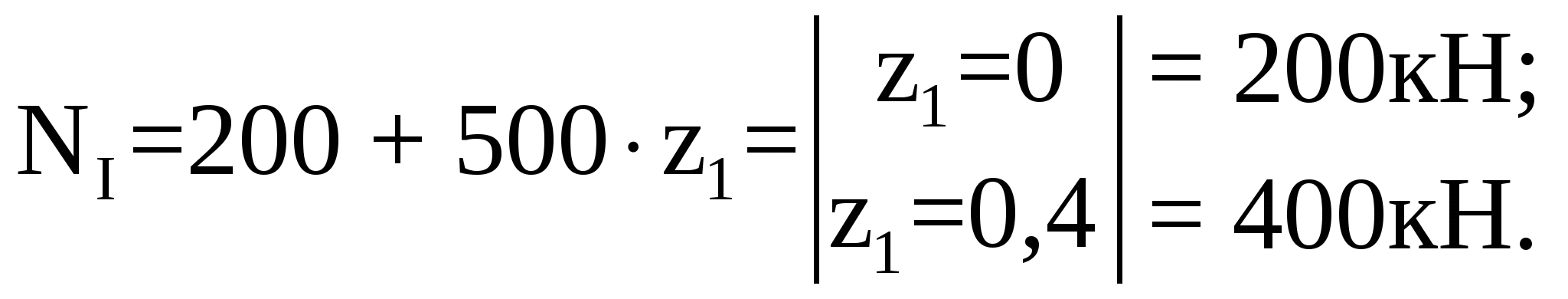
Аналогично рассмотрим участок II (ВС): 
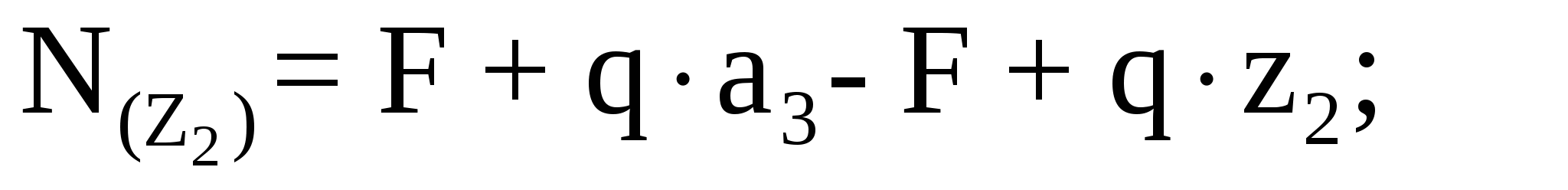
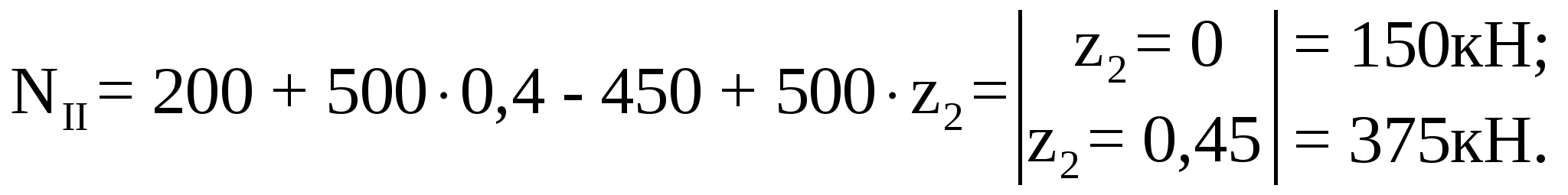
Аналогично рассмотрим участок III (СD): 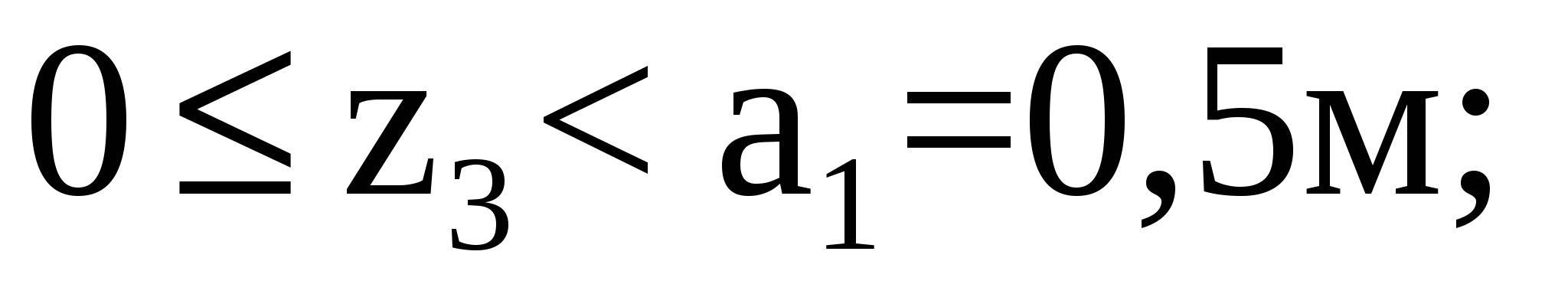
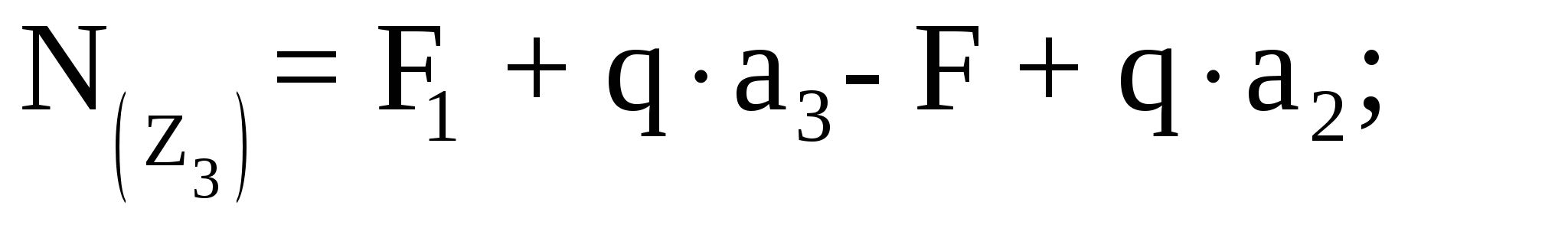
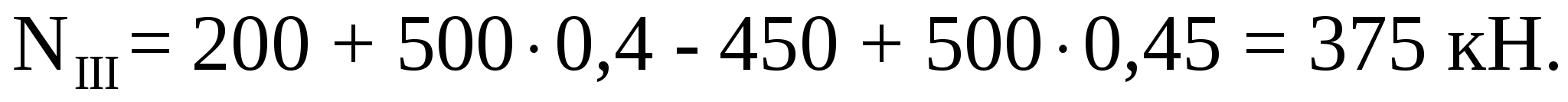
По полученным значениям строим эпюру продольной силы (рисунок 1).
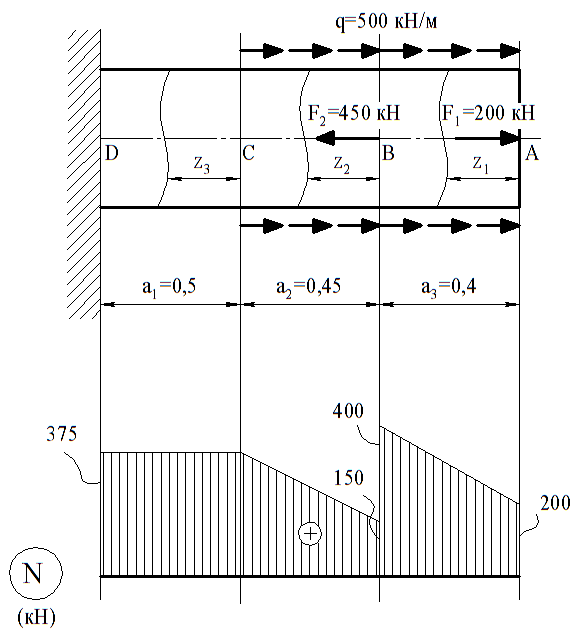
Рисунок 1 – Расчетная схема стержня
Задача 2
Построение эпюры крутящего момента
Исходные данные:  а = 1 м. а = 1 м.


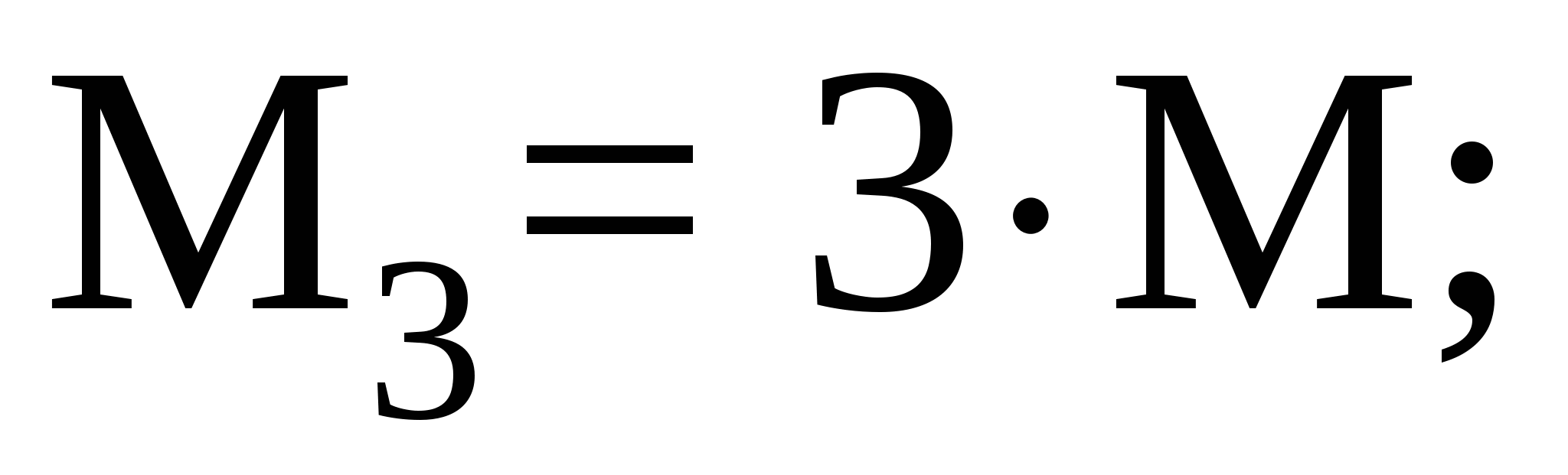
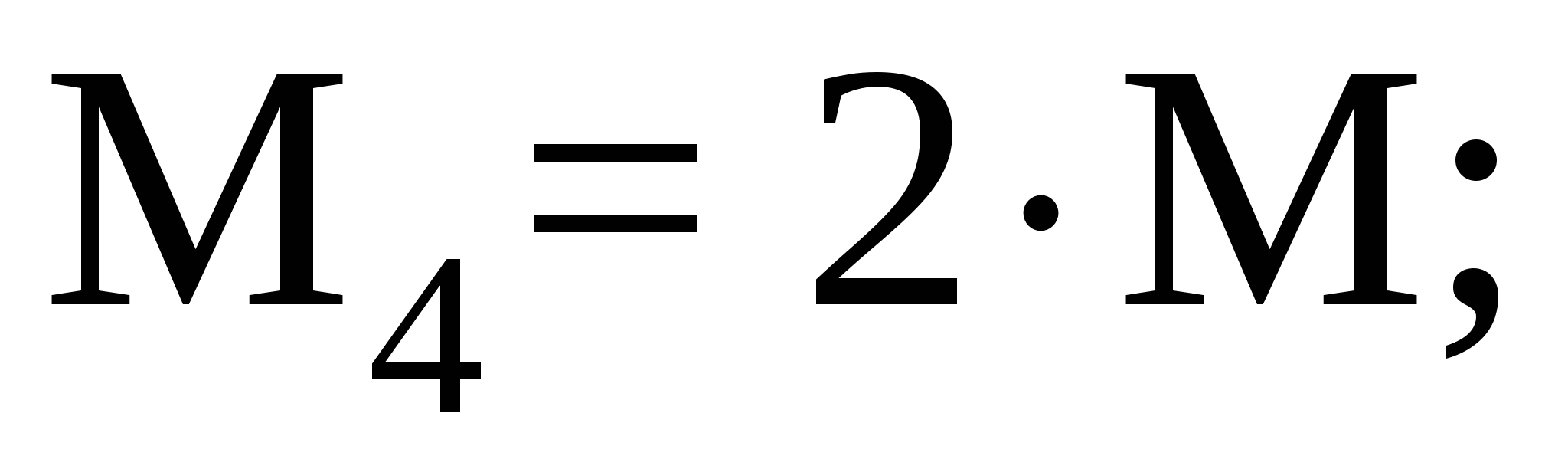


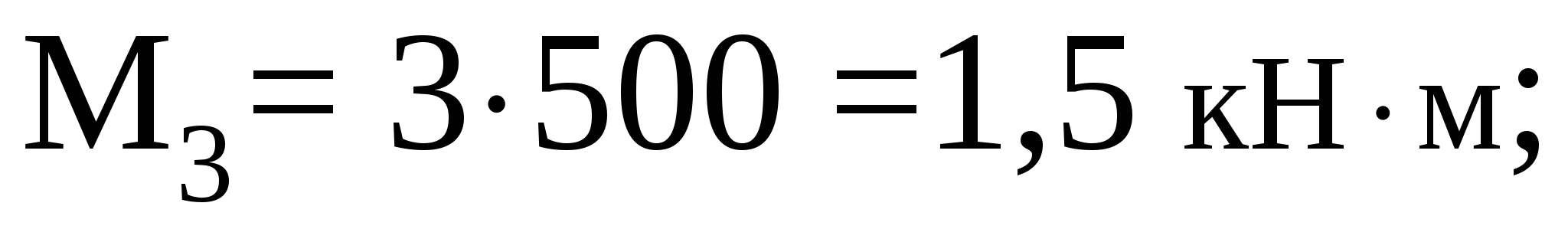
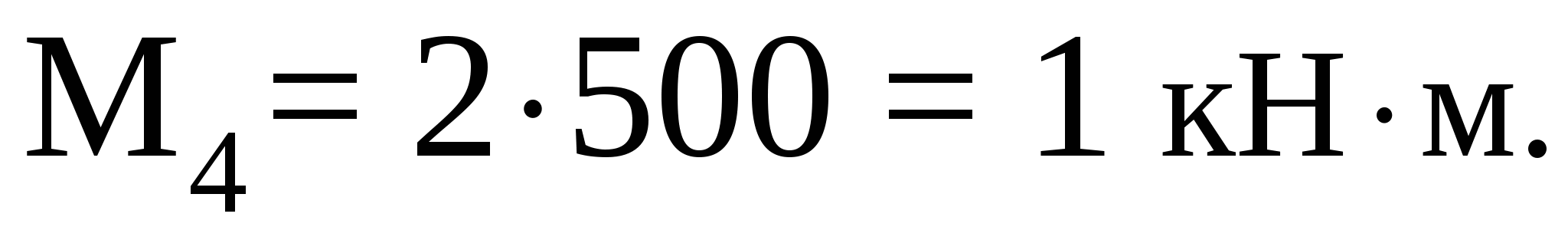
Заданная схема вала представлена на рисунке 2.1.

Рисунок 2.1 – Заданная схема вала
Решение
Вычерчиваем расчетную схему вала с указанием всех размеров в масштабе и приложенных нагрузок ( рисунок 2.2).
Разбиваем вал на четыре силовых участка AB, BC, CD и DE (рисунок 2.2). Для каждого участка применяем метод сечений, составляем уравнения крутящего момента, по которым определяем характерные ординаты.
Рассмотрим участок I (АВ): 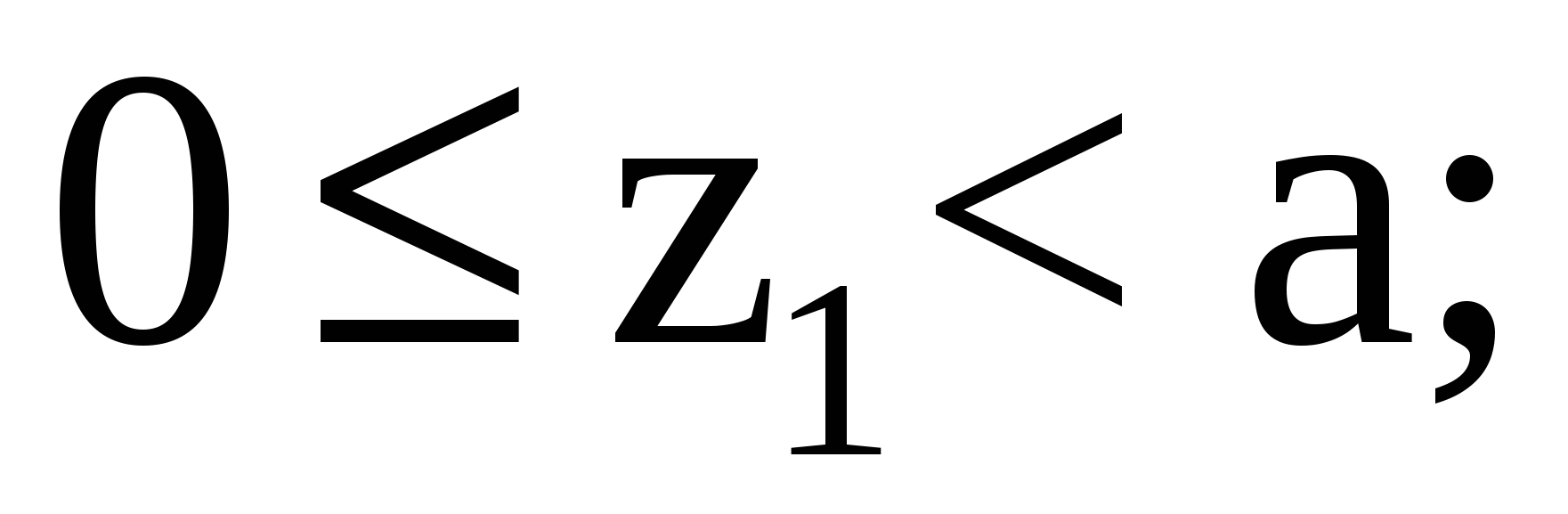
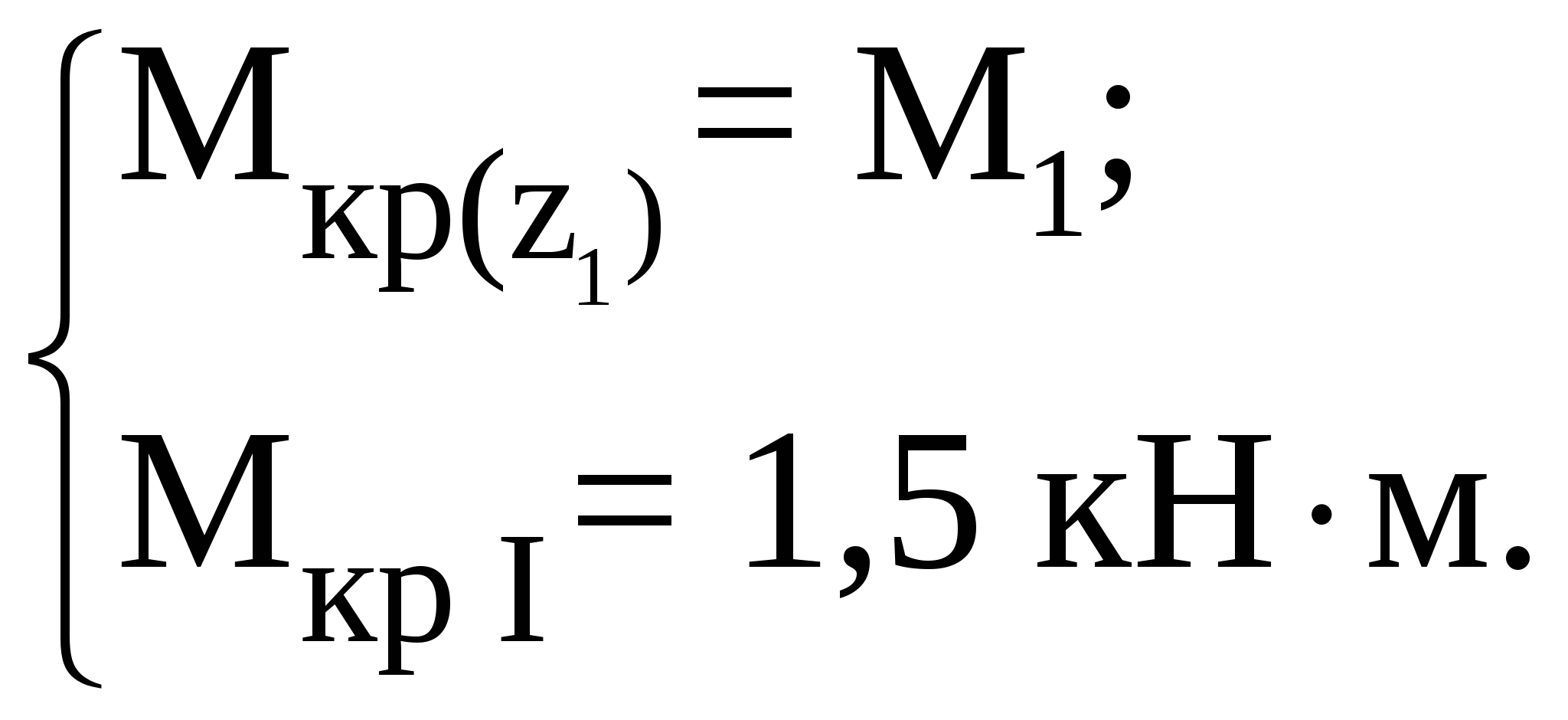
Рассмотрим участок II (ВC): 

Рассмотрим участок III (CD): 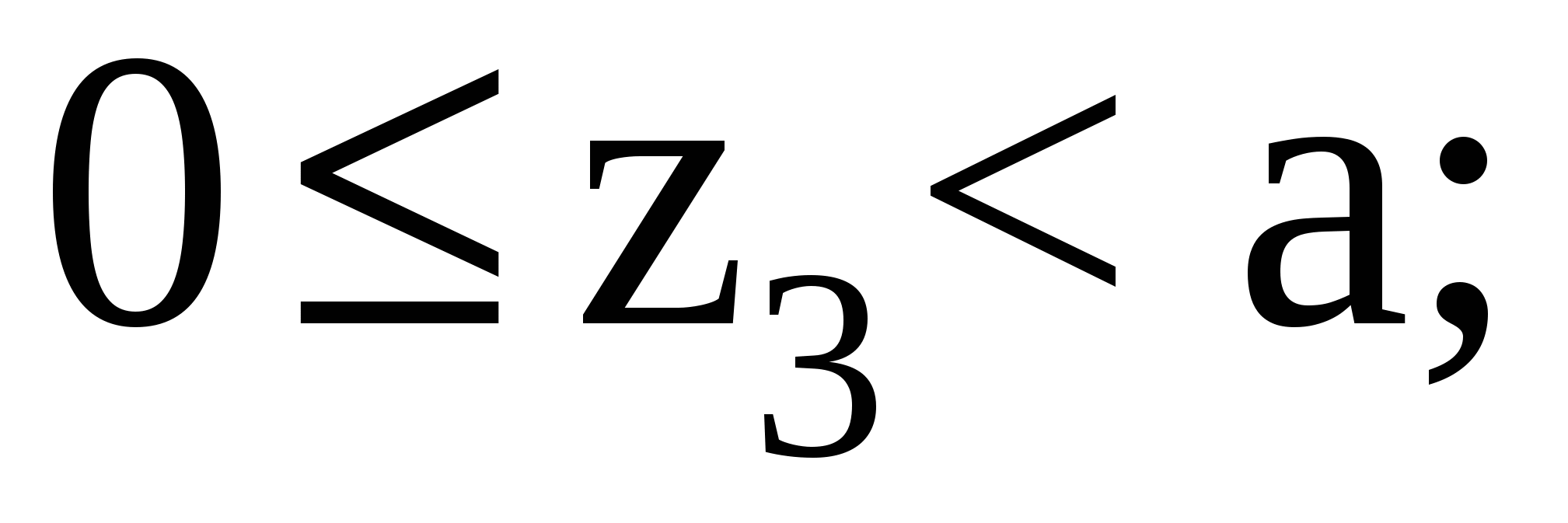
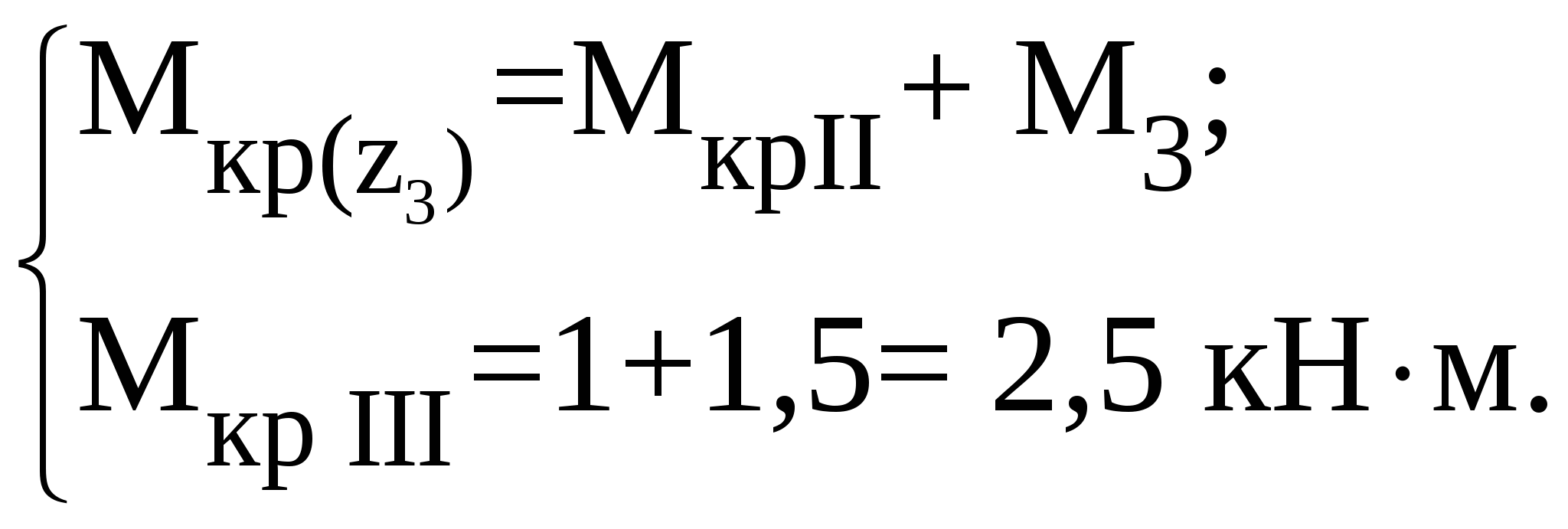
Рассмотрим участок IV (DE): 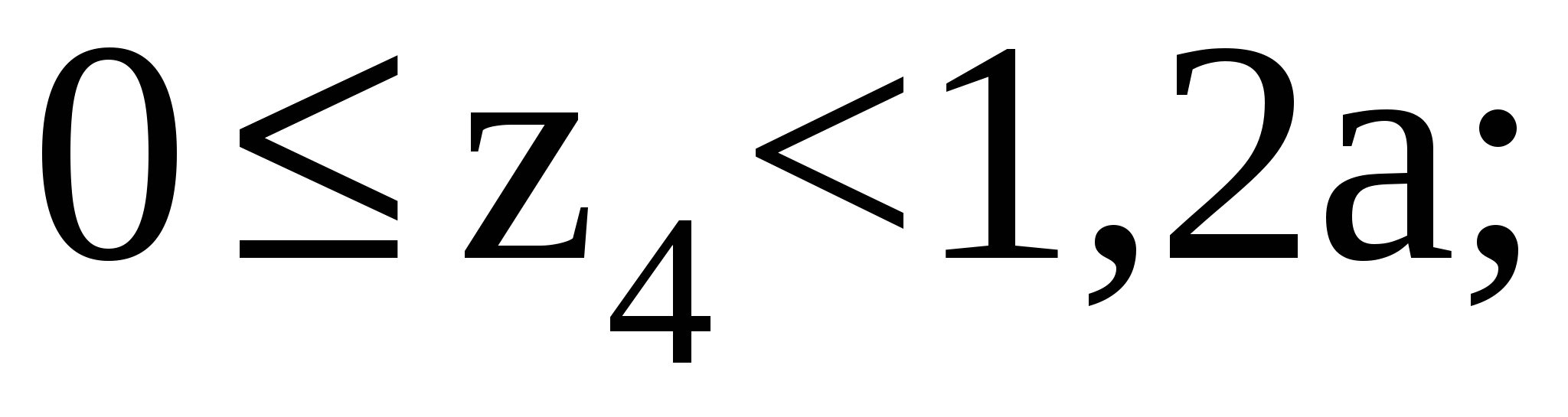
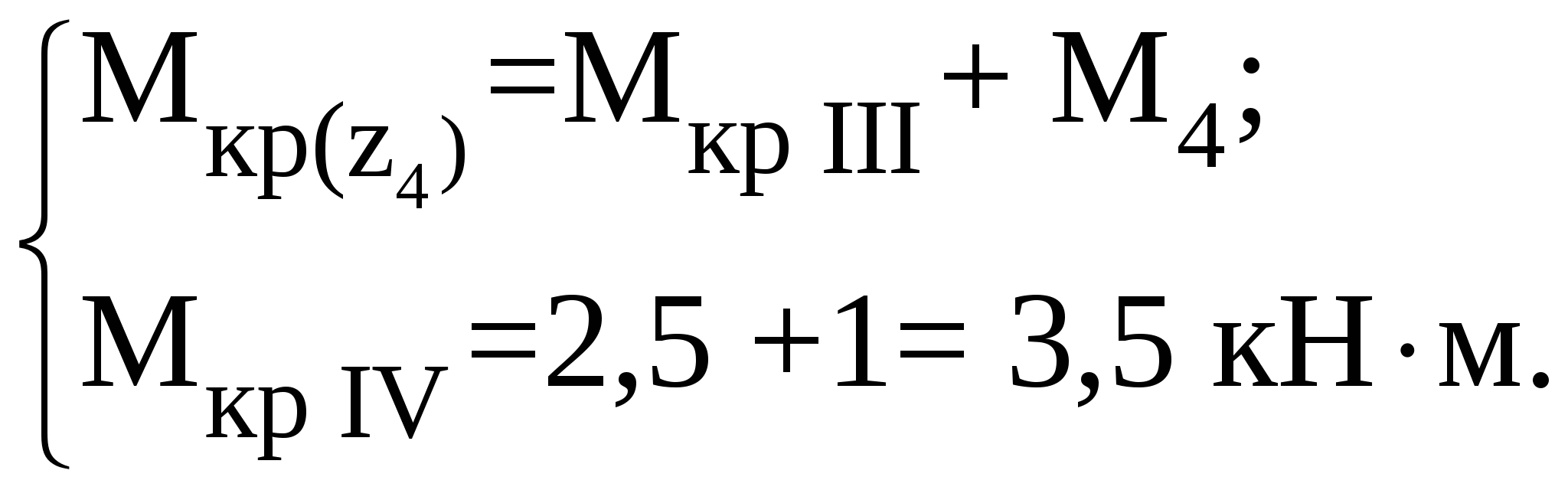
По полученным значениям строим эпюру крутящего момента (рисунок 2.2).

Рисунок 2.2 – Расчетная схема вала
Задача 3
Построение эпюры поперечной силы и изгибающего момента для защемленной балки
Исходные данные: F=1,8qa; М=1,6qa2;
Заданная схема защемленной балки представлена на рисунке 3.1.

Рисунок 3.1 – Заданная схема защемленной балки
Решение
Вычерчиваем расчетную схему защемленной балки с указанием всех размеров в масштабе и приложенных нагрузок( рисунок 3.2).
Разбиваем балку на силовые участки. Для каждого участка применяем метод сечений, составляем уравнения сил и изгибающего момента, решая которые строим их эпюры.
Рассмотрим участок I (AB): 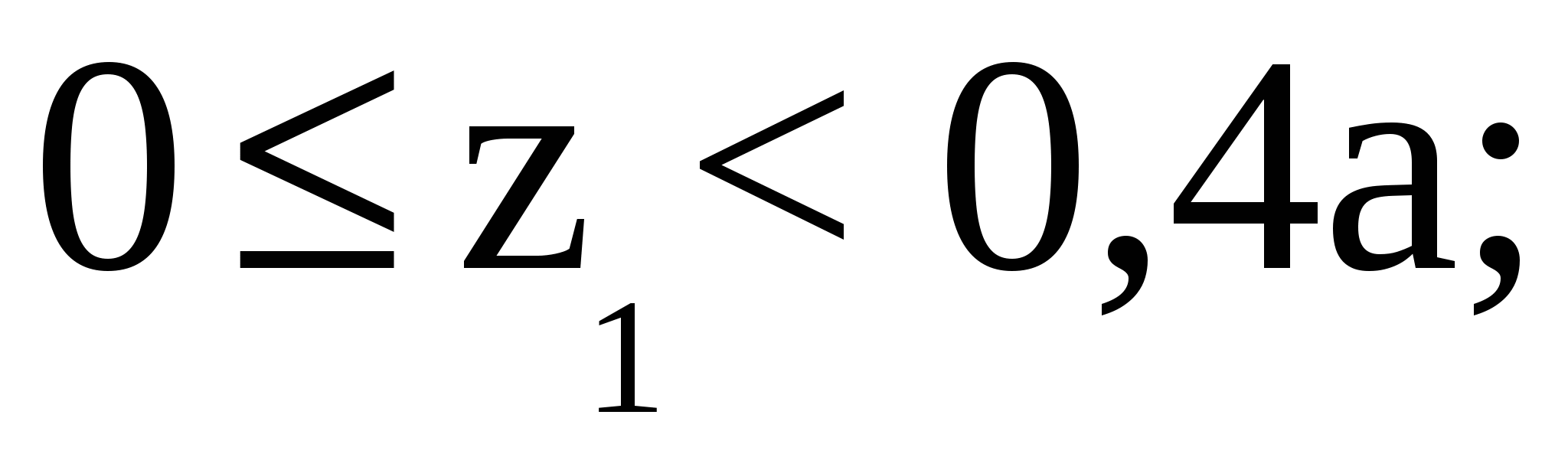
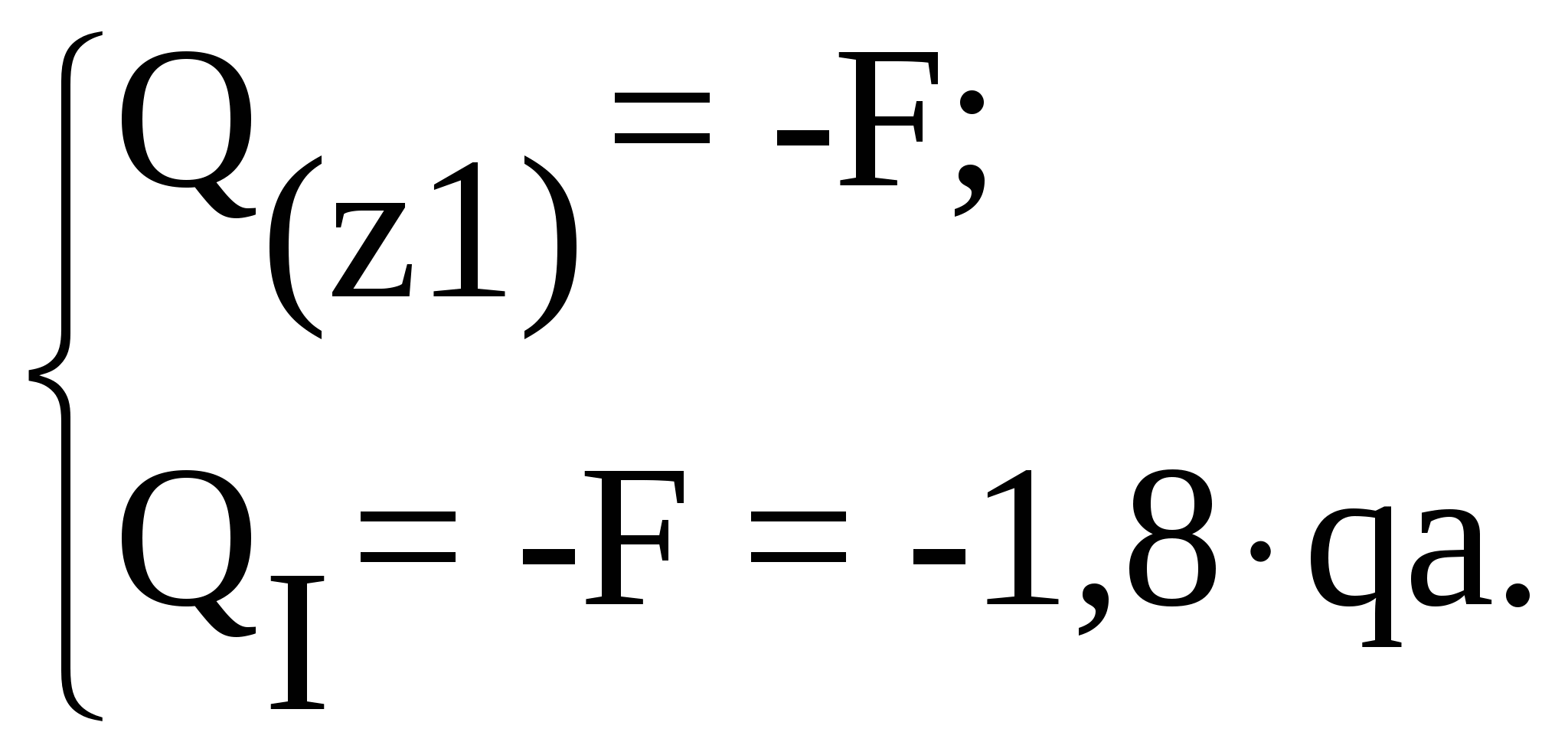
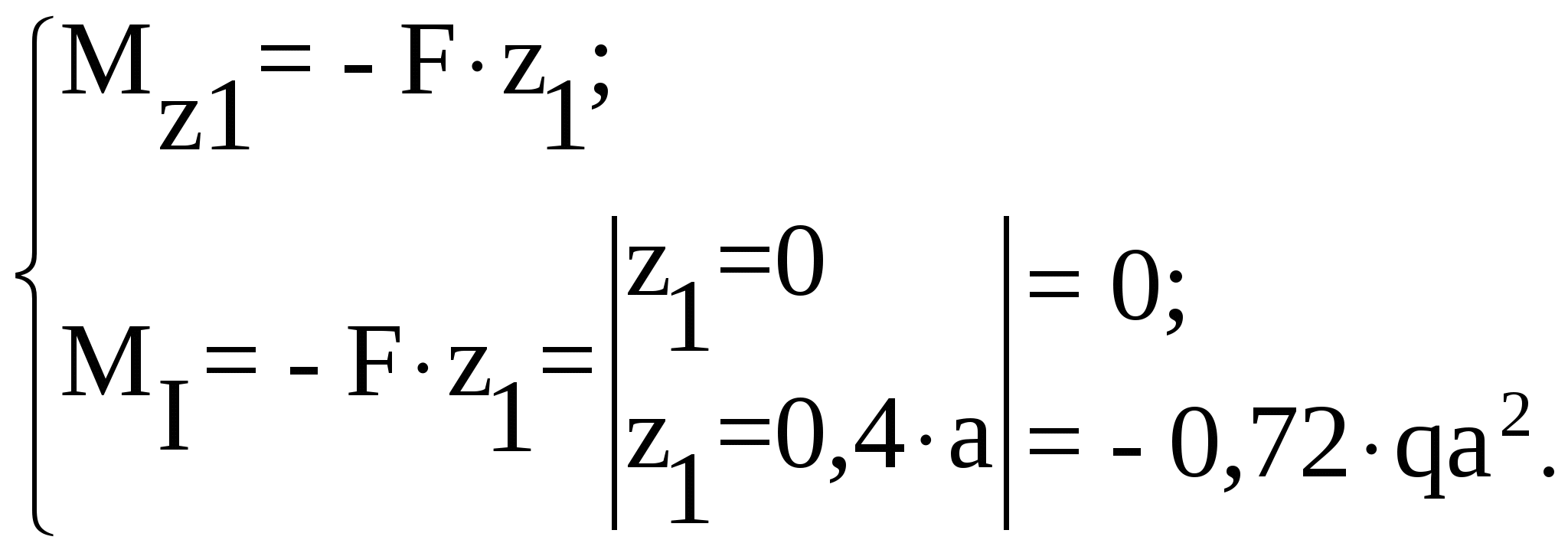
Рассмотрим участок II (BC): 

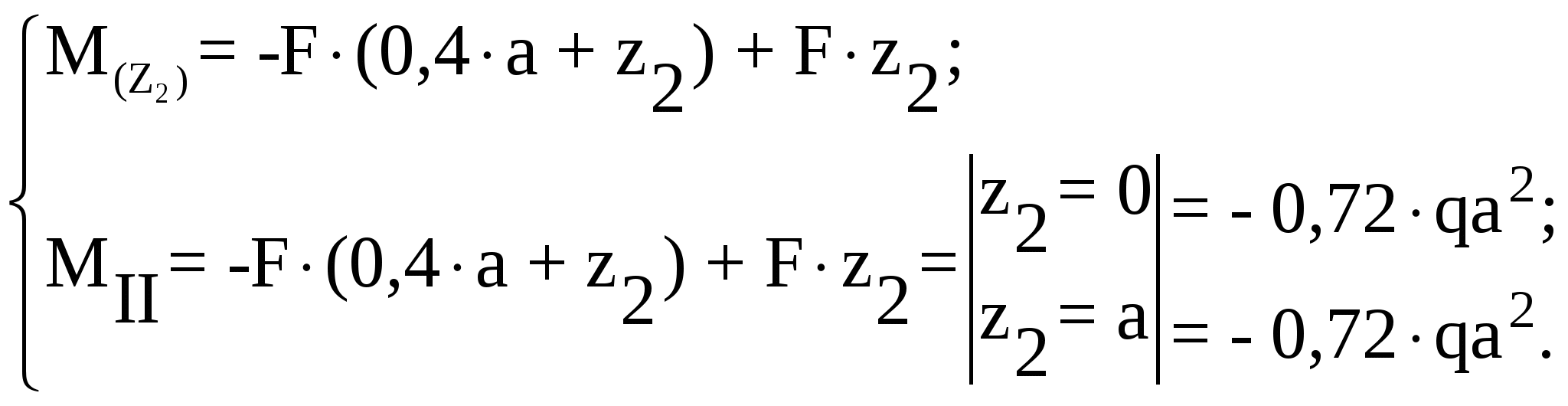
Рассмотрим участок III (CD): 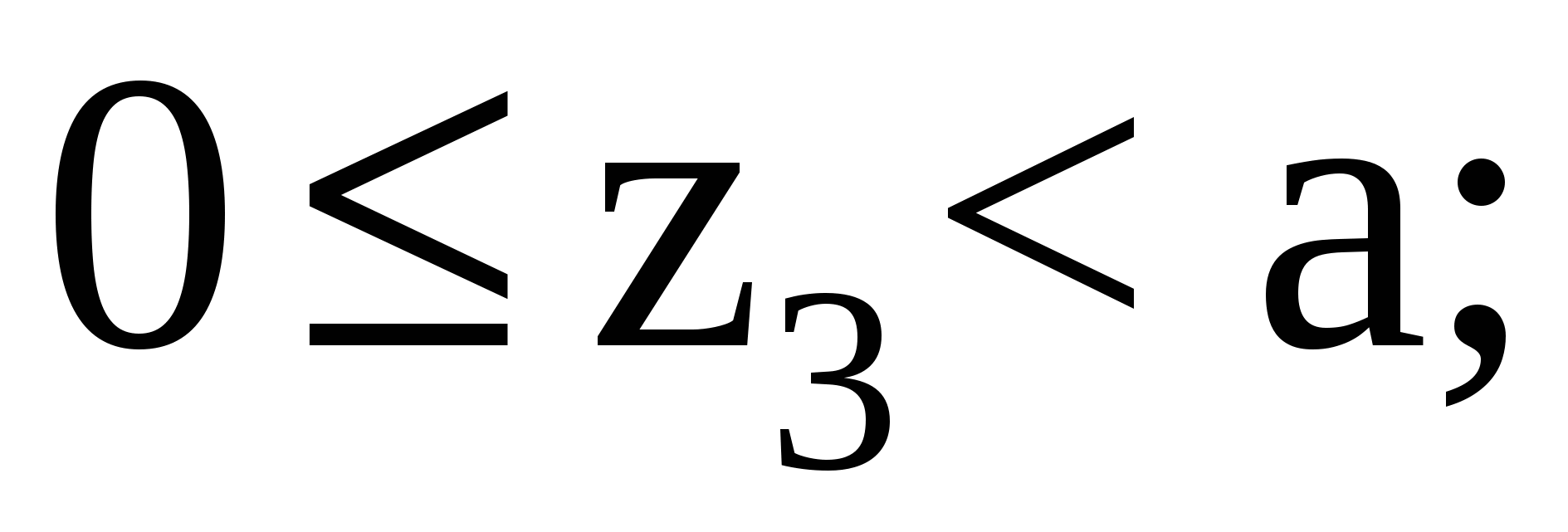
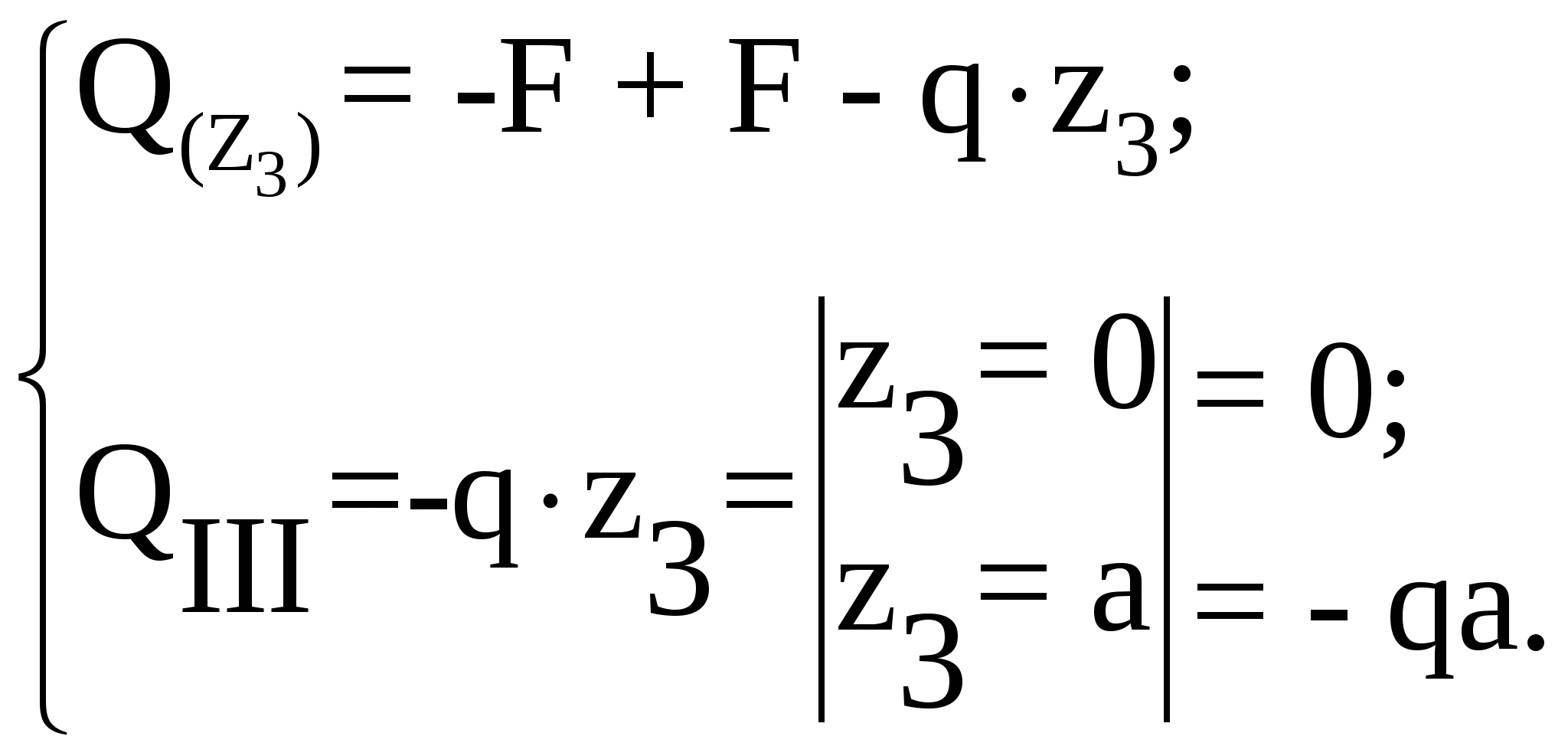

По полученным значениям поперечной силы и изгибающего момента построим их эпюры (рисунок 3.2).
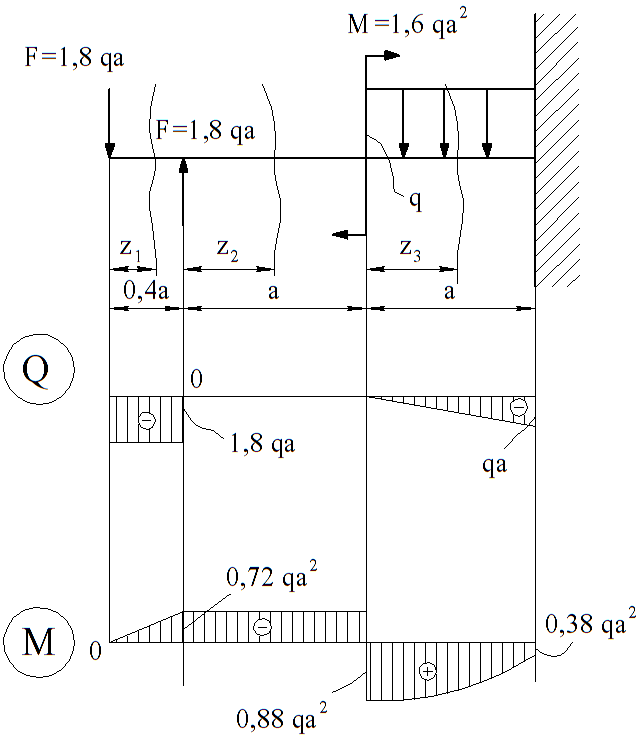
Рисунок 3.2 – Расчетная схема защемленной балки
Задача 4
Построение эпюры поперечной силы и изгибающего момента для простой балки
Исходные данные: F=1,8qa; М=1,6qa2.
Заданная схема простой балки приведена на рисунке 4.1.
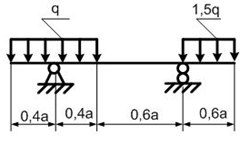 Рисунок 4.1 – Заданная схема простой балки Решение
Вычерчиваем исходную схему простой балки (рисунок 4.2).Определяем реакции опорных связей.
Составим уравнение проекций на ось x:


Составим уравнение моментов относительно опоры B:
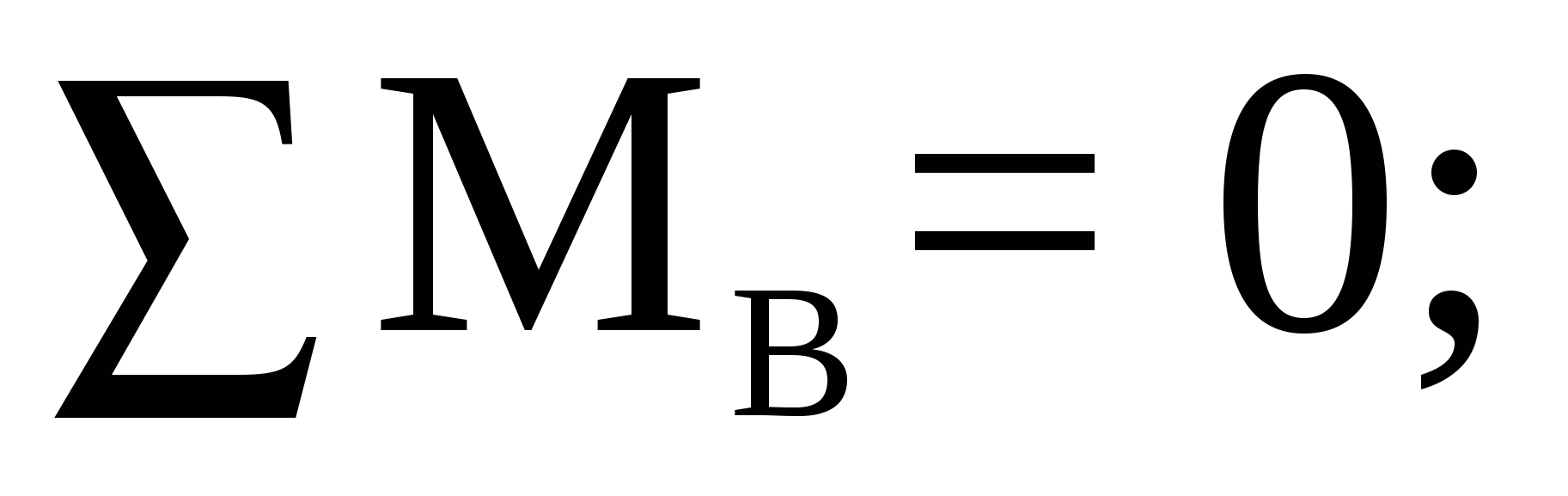
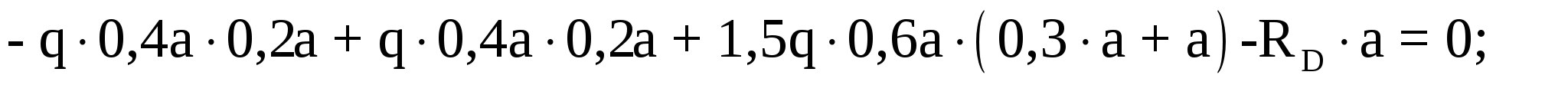
отсюда находим реакцию опоры D:


Аналогично составим уравнение моментов относительно опоры D:
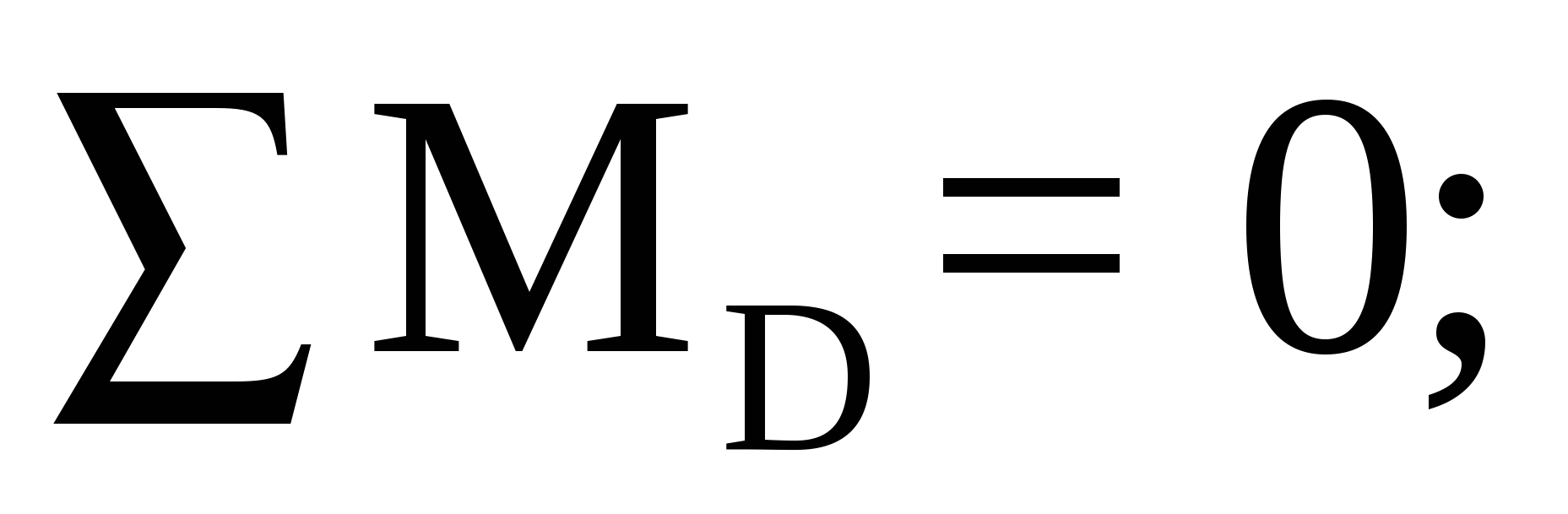

из которого находим реакцию опоры:


Для проверки составим уравнение проекций всех сил на ось y:
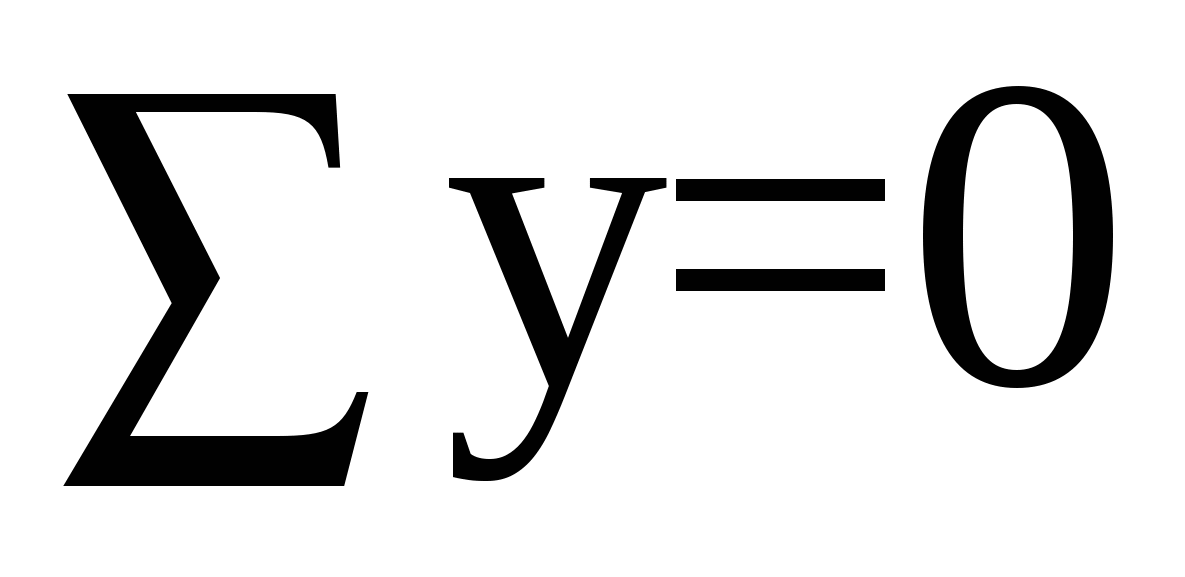
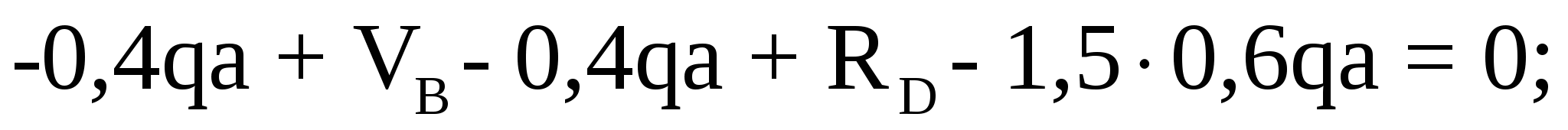


Условие проверки выполняется, следовательно, проведенные выше вычисления реакций опор верны.
Разбиваем балку на силовые участки (рисунок 4.2), для каждого участка применяем метод сечений и составляем уравнения поперечной силы и изгибающего момента. Определяем характерные ординаты поперечной силы и изгибающего момента.
Рассмотрим участок І (AB): 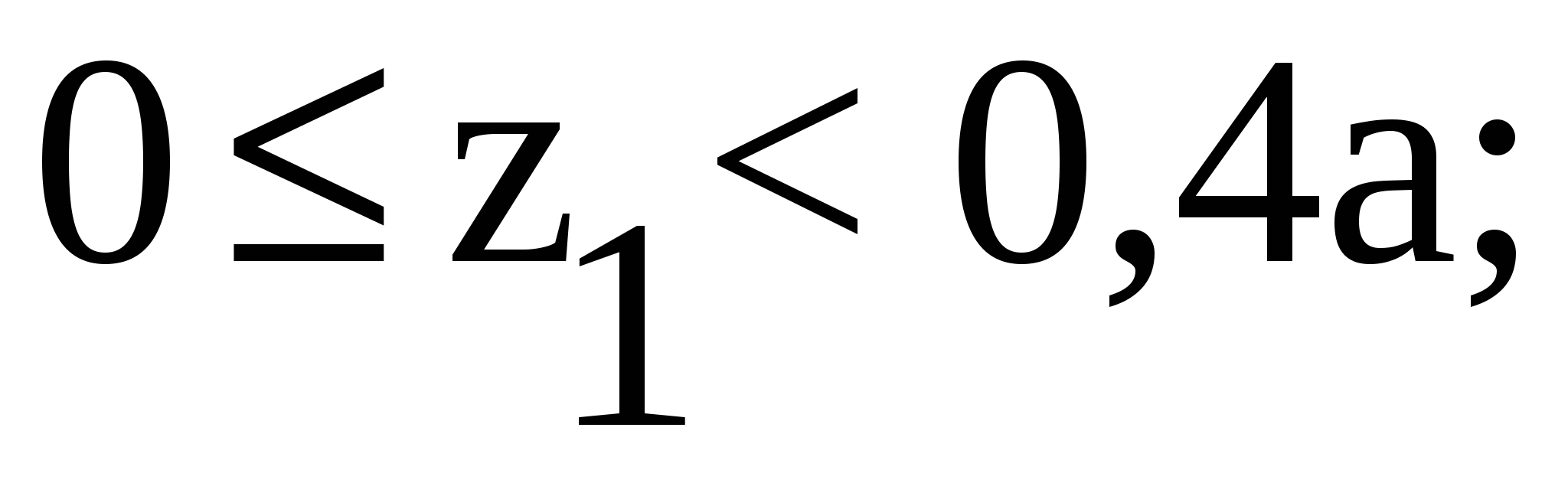
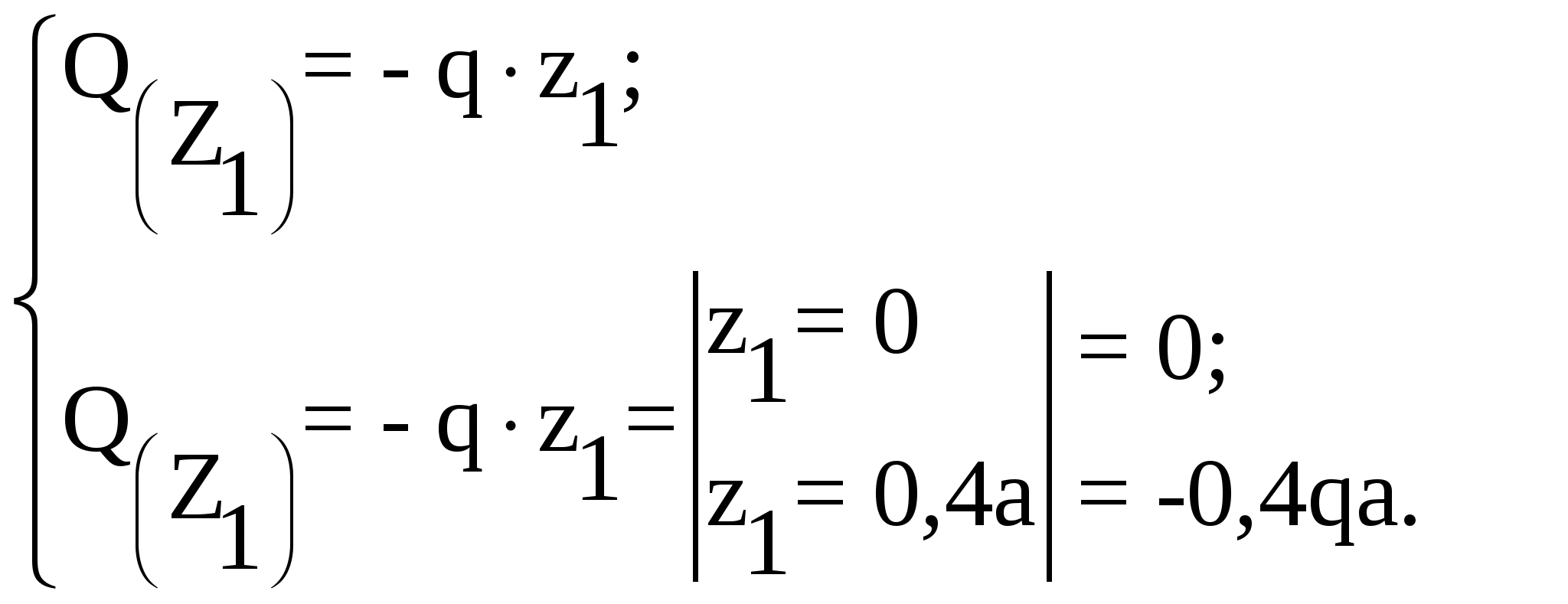

Рассмотрим участок II (BC): 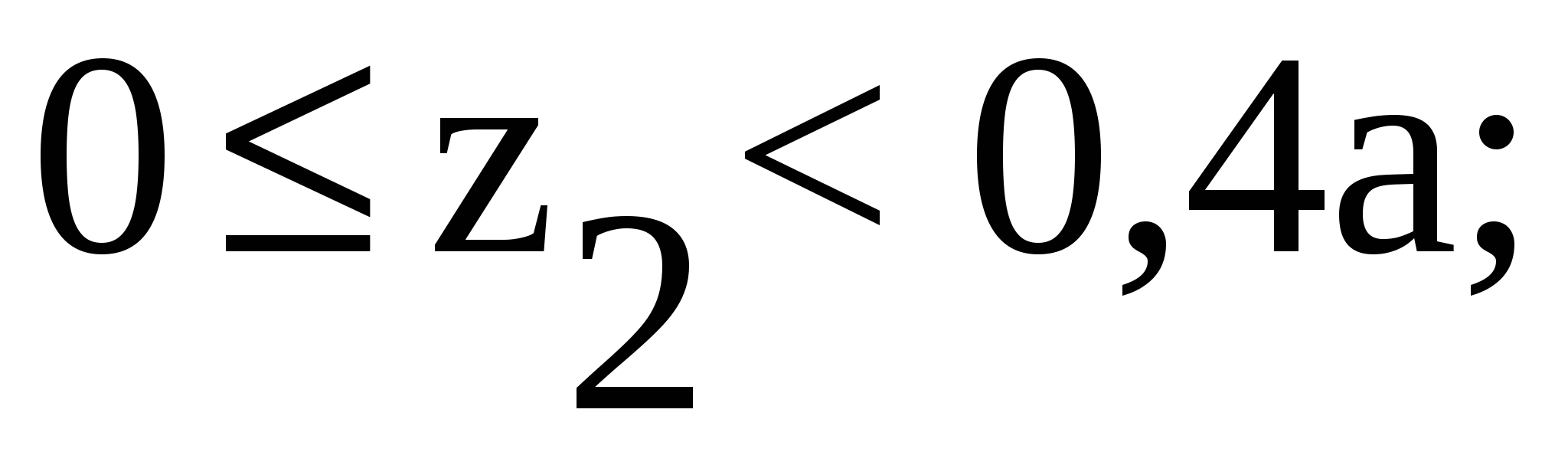
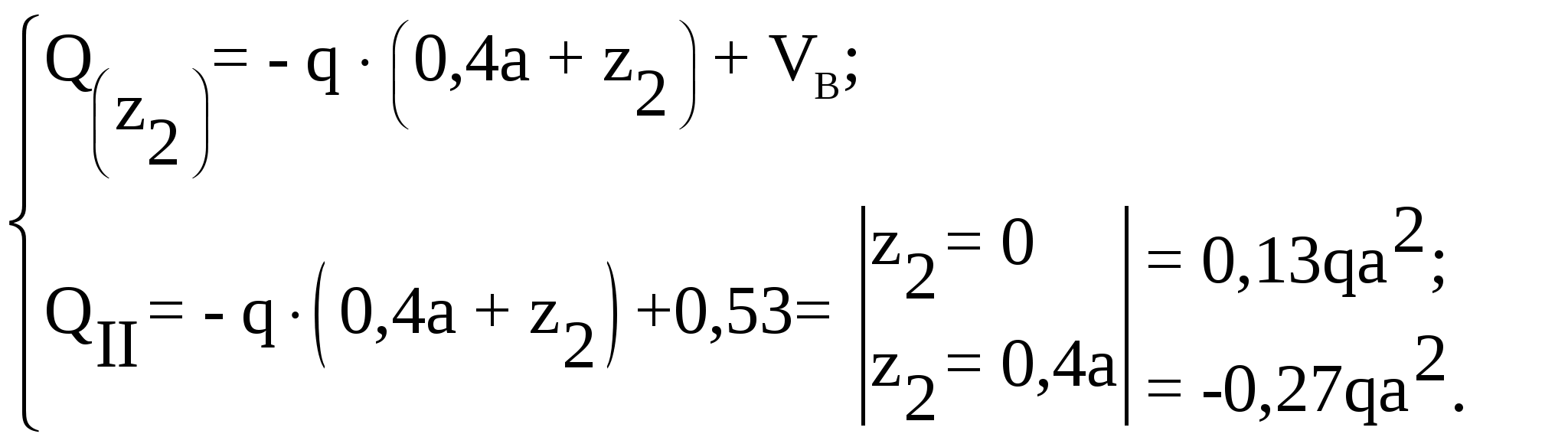

Рассмотрим участок III (CD):

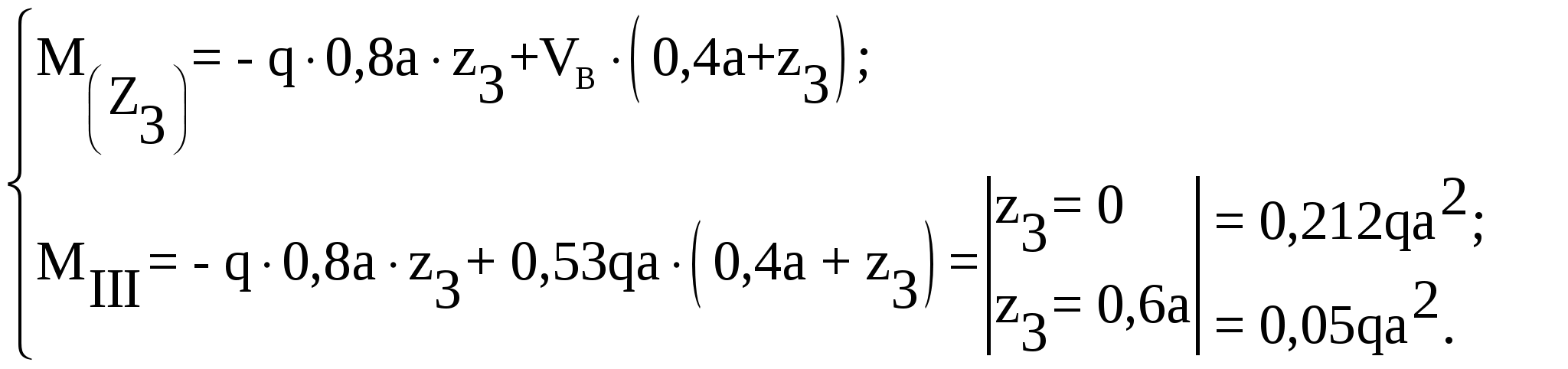
Рассмотрим участок IV (DE): 

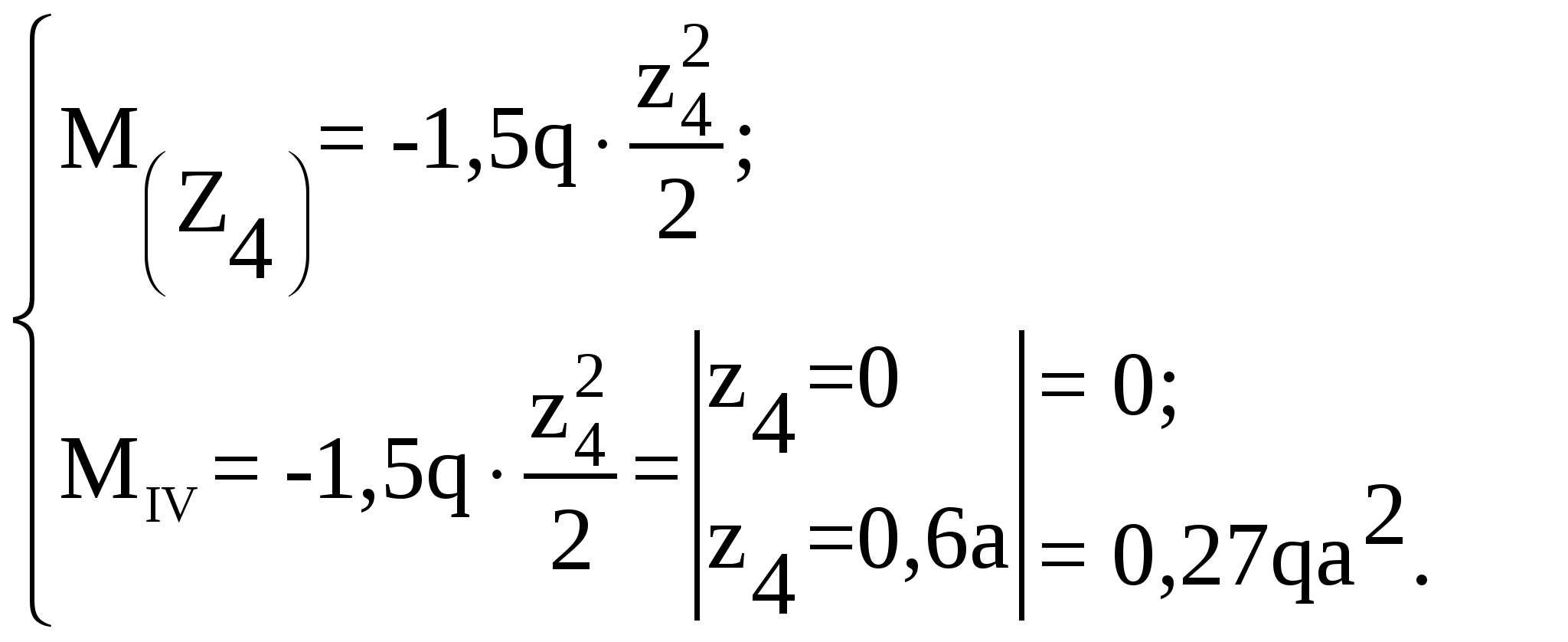
По полученным значениям ординат поперечной силы и изгибающего
м
омента строим их эпюры (рисунок 4.2).
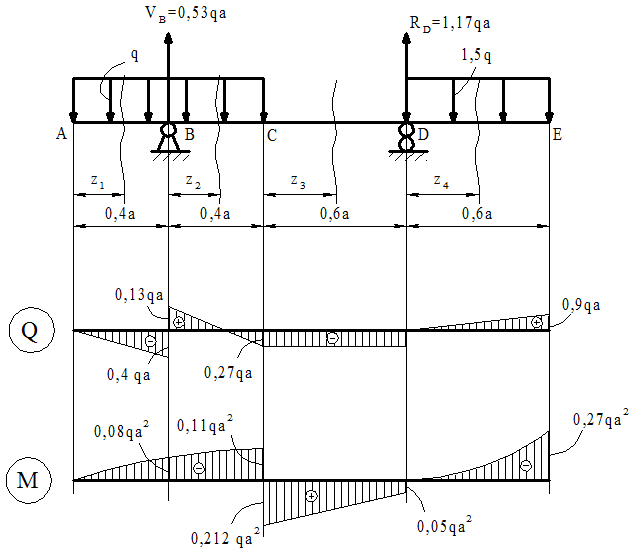
Рисунок 4.2 – Расчетная схема простой балки
Задача 5
Построение эпюр поперечной силы и изгибающего момента для балки с шарниром.
Исходные данные: F = 1,8qa; М = 1,6qa2.
Заданная схема балки с шарниром представлена на рисунке 5.1.

Рисунок 5.1 – Заданная схема балки с шарниром
Решение
Вычерчиваем расчетную схему балки с указанием всех размеров в масштабе и приложенных нагрузок (рисунок 5.2). Определяем реакции опор балки, записав уравнения равновесия.
Составим уравнение моментов относительно вращательного шарнира B для левой части балки:
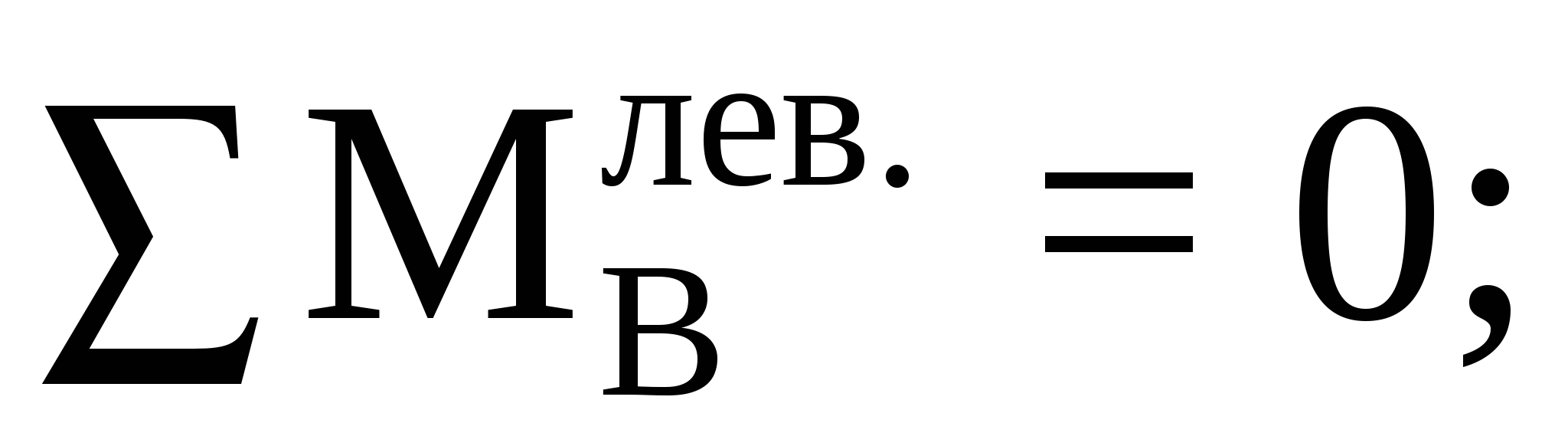

Составим уравнение моментов относительно опоры С:
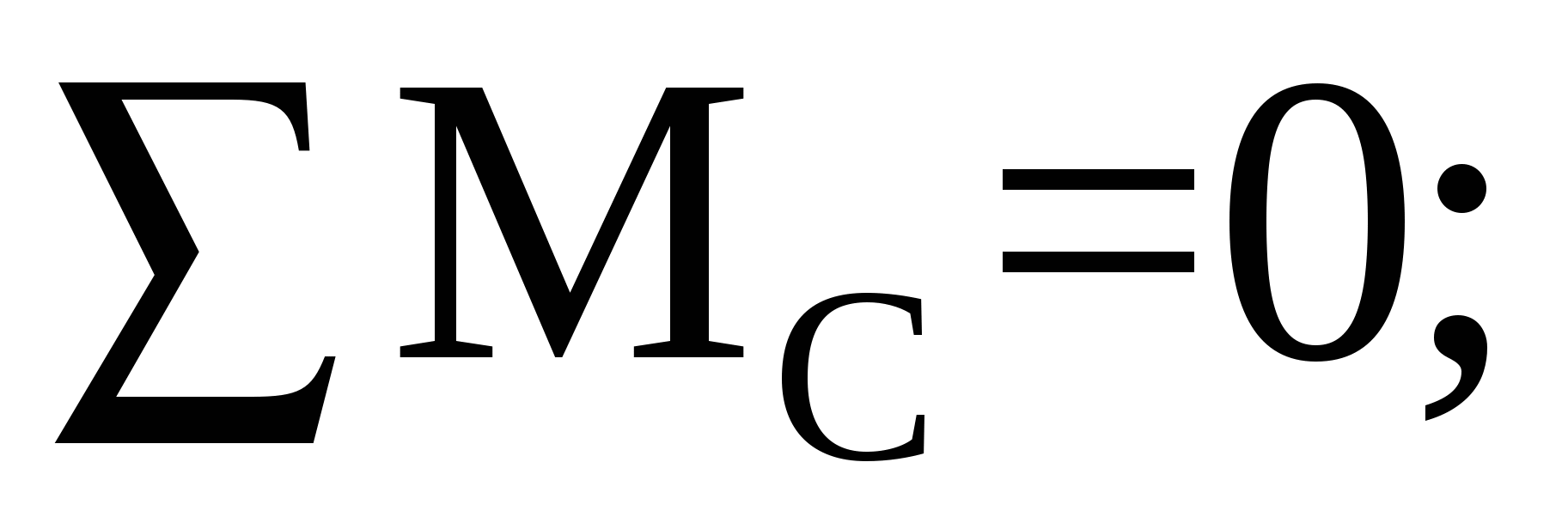
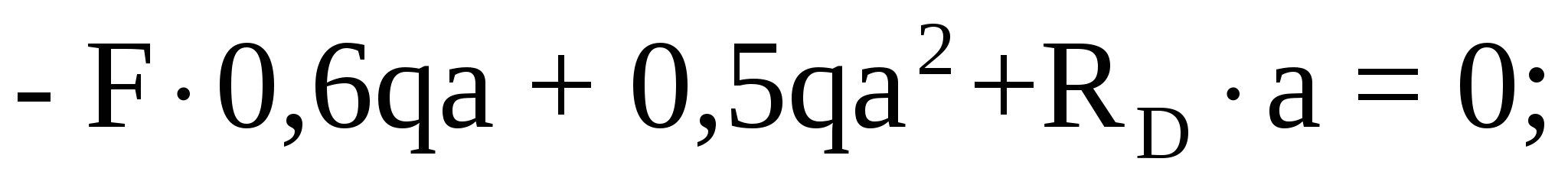
отсюда находим вертикальную реакцию в опоре D:

Составим уравнение моментов относительно опоры D:


отсюда находим вертикальную реакцию в опоре C:

Для проверки найденных реакций опор составим уравнение проекций всех сил на ось y:

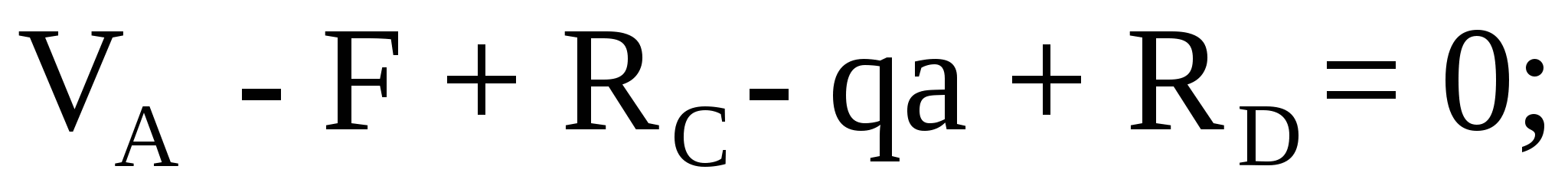
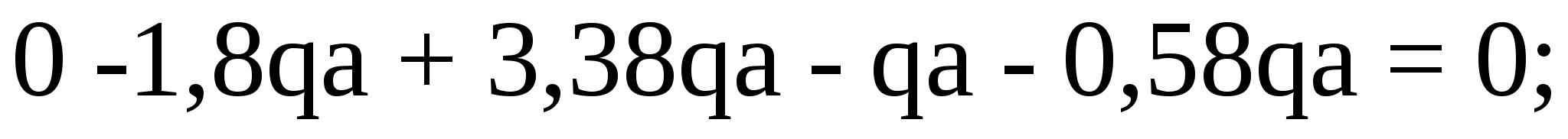

Условие проверки выполняется, следовательно, проведенные выше вычисления реакций опор верны.
Разбиваем балку на три силовых участка АВ, ВС и CD (рисунок 5.2). Применяя метод сечений, строим эпюры поперечной силы и изгибающего момента.
Рассмотрим участок I (AB): 


Рассмотрим участок II (ВС): 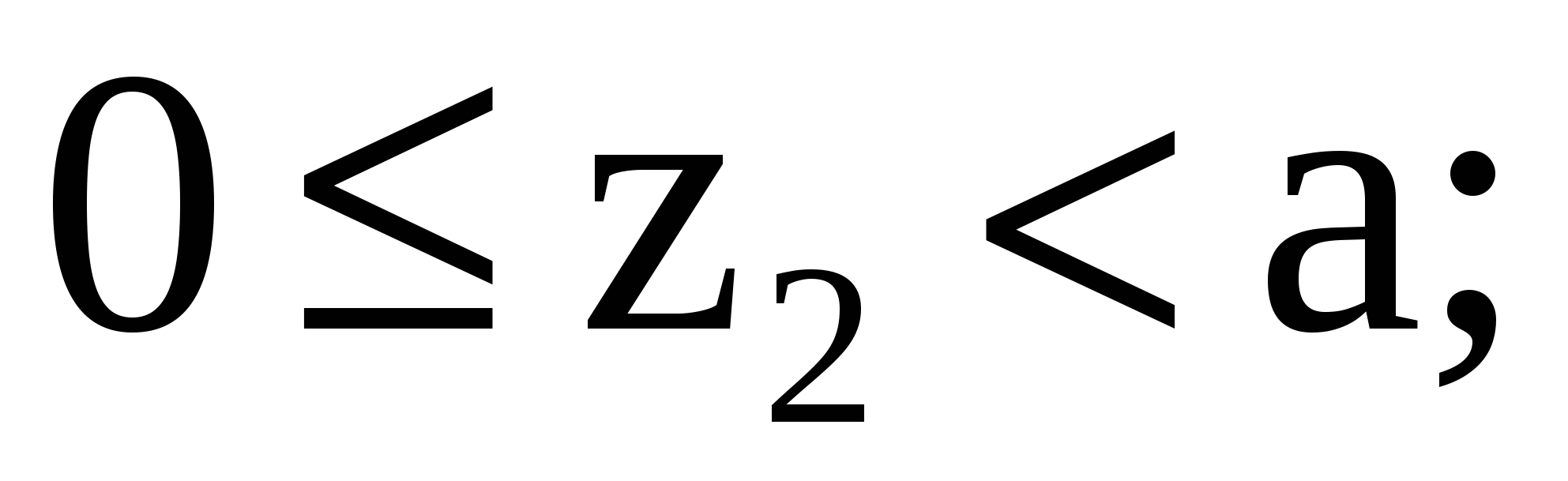
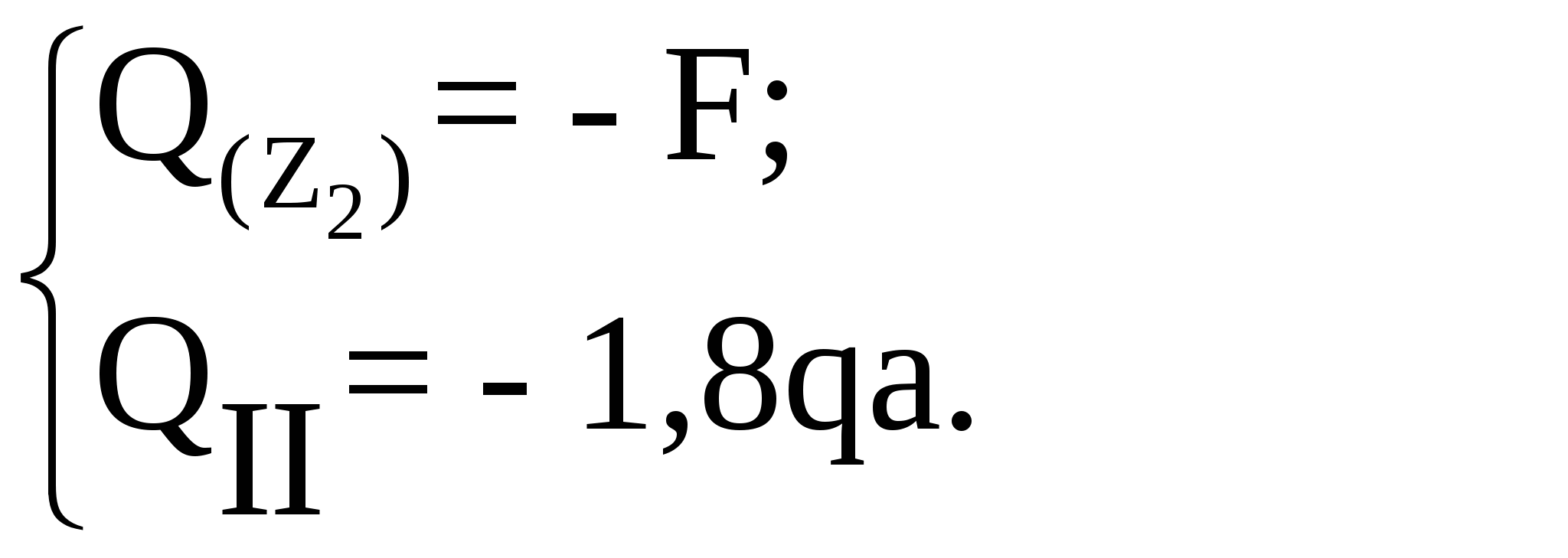

Рассмотрим участок III (CD): 
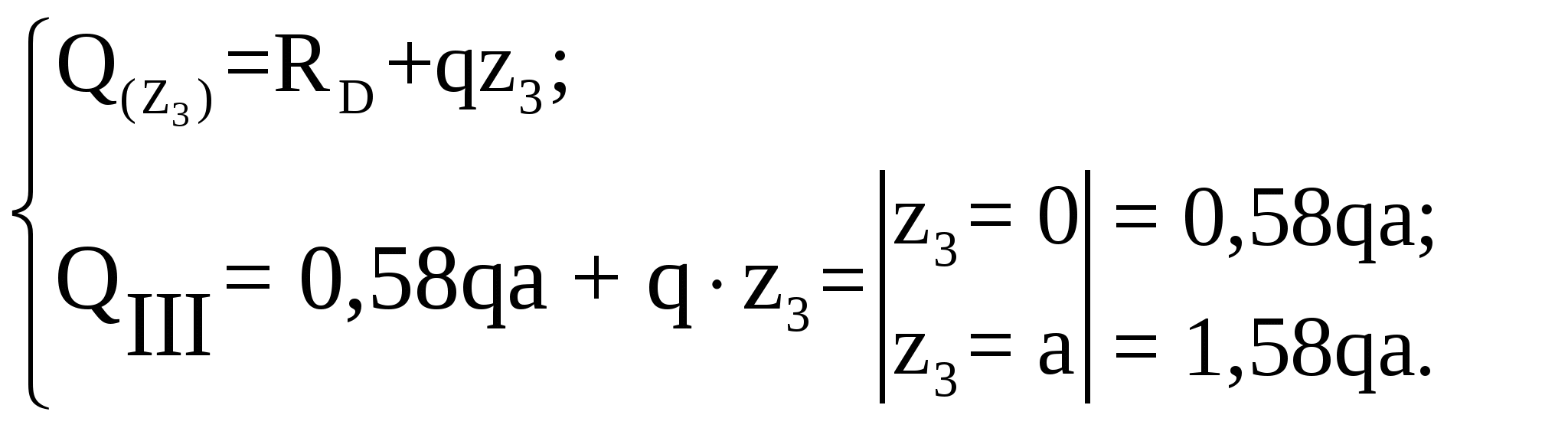
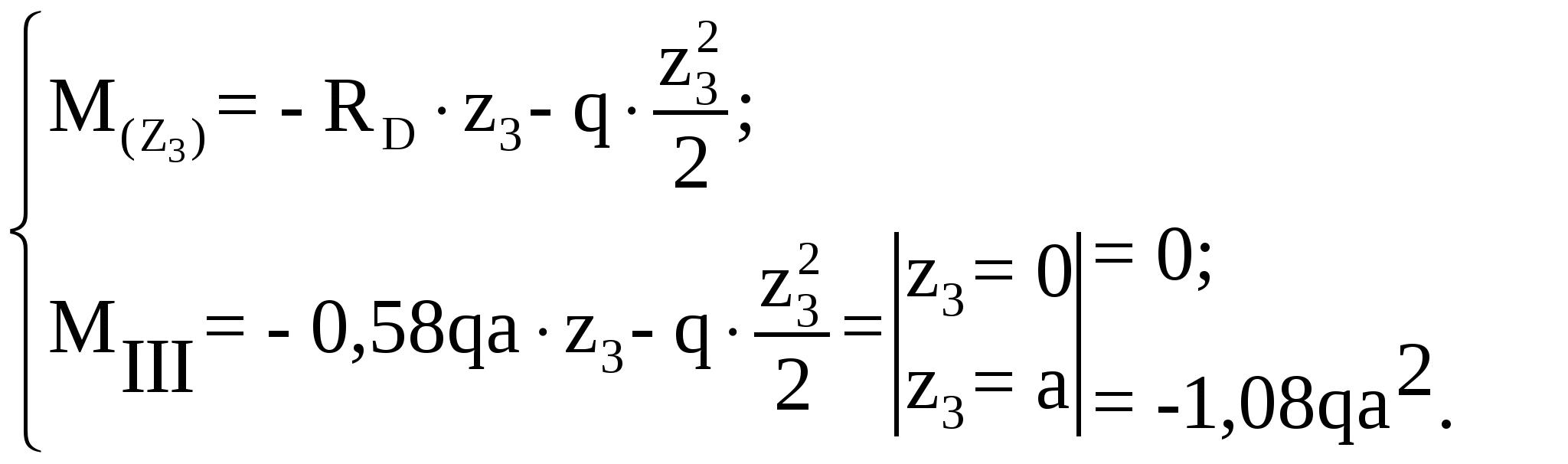
По полученным значениям ординат поперечной силы и изгибающего
момента строим их эпюры (рисунок 5.2).

Рисунок 5.2 – Расчетная схема балки с шарниром
Задача 6
Построение эпюр продольной, поперечной силы и изгибающего момента для рамы
Исходные данные: F=1,8qa; М=1,6qa2.
Заданная схема рамы представлена на рисунке 6.1.

Рисунок 6.1 – Заданная схема рамы
Решение
Изображаем расчетную схему рамы в масштабе с указанием всех нагрузок (рисунок 6.2).
Определяем реакции опор.
Составим уравнение проекций сил на ось x:

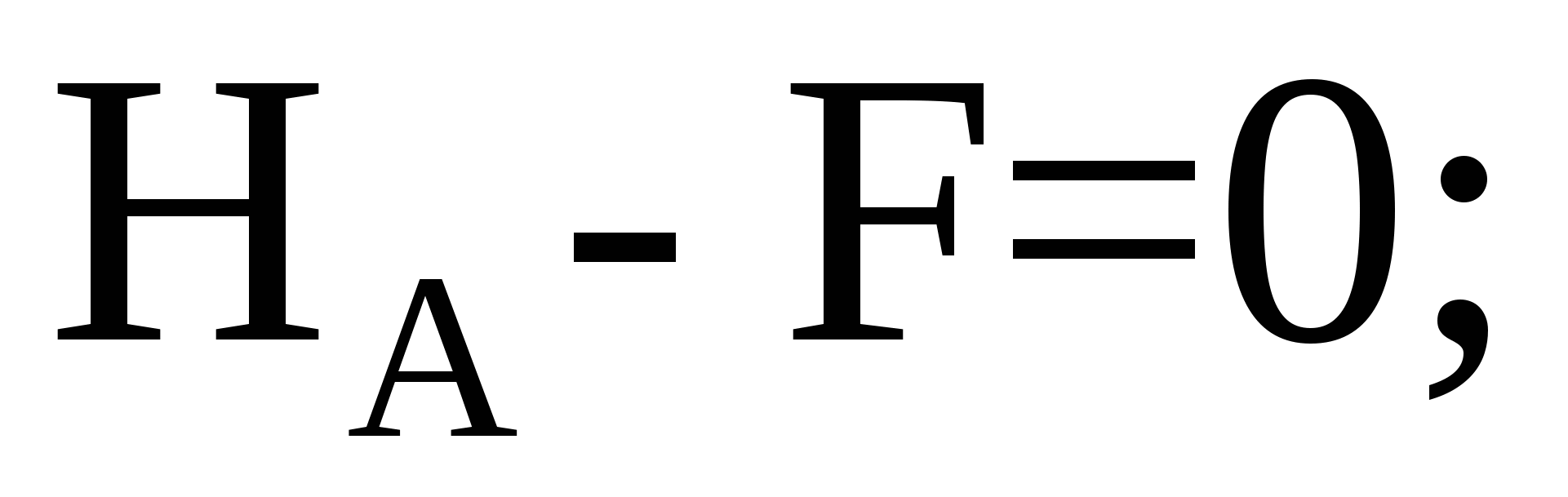
отсюда определим горизонтальную силу в опоре А:

Составим уравнение моментов сил относительно опоры А:
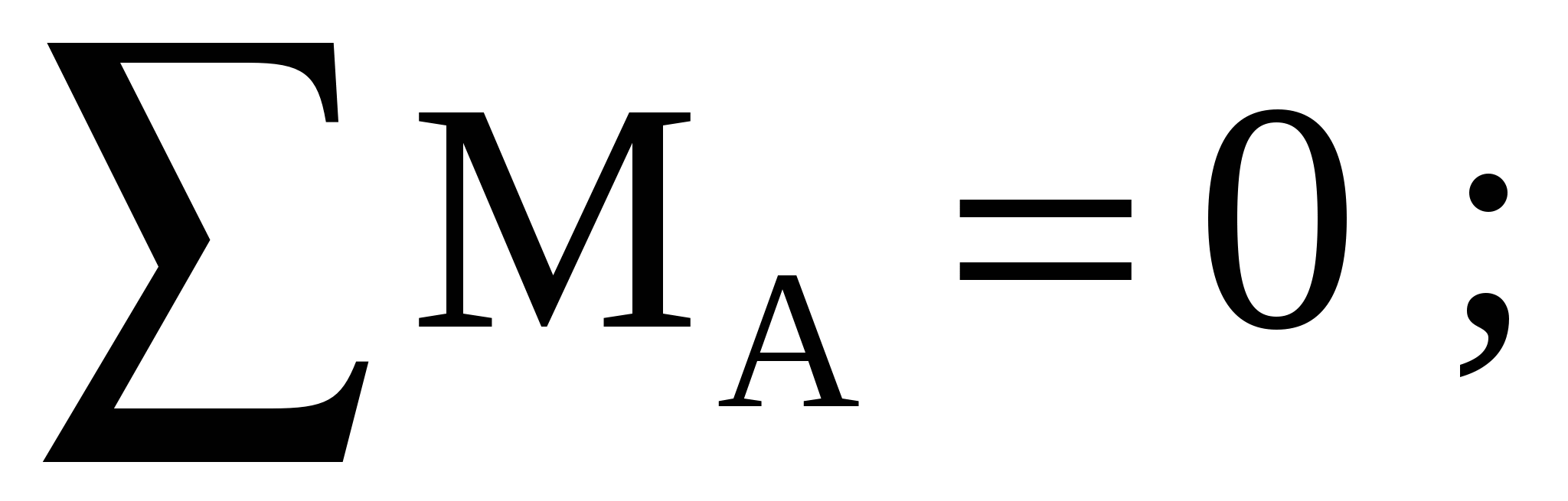

отсюда выразим реакцию в опоре B:

Аналогично составим уравнение моментов относительно точки B:

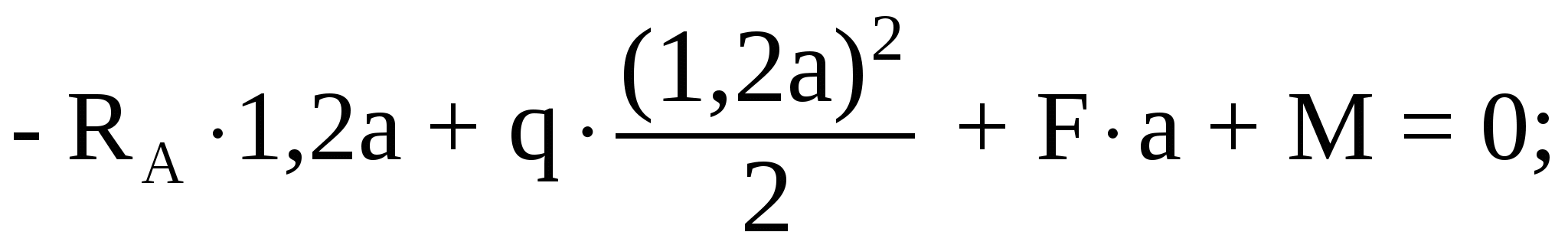
отсюда определим вертикальную реакцию опоры А:
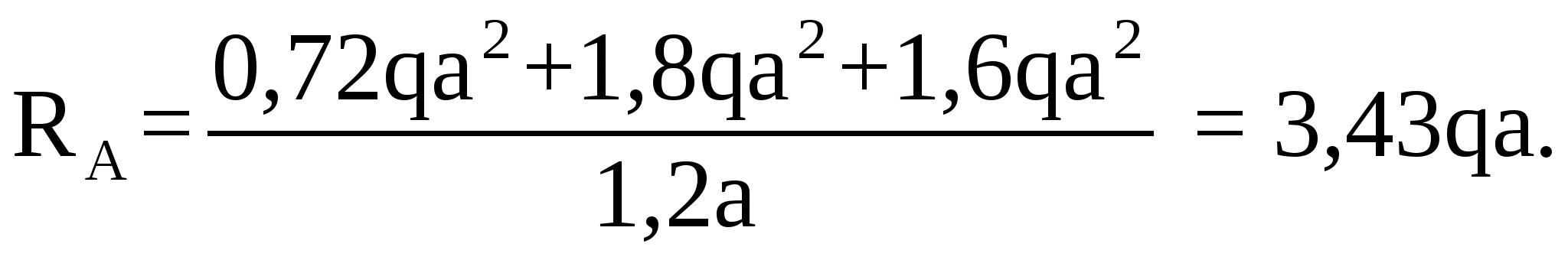
Для проверки найденных реакций опор составим уравнение проекций всех сил на ось y:
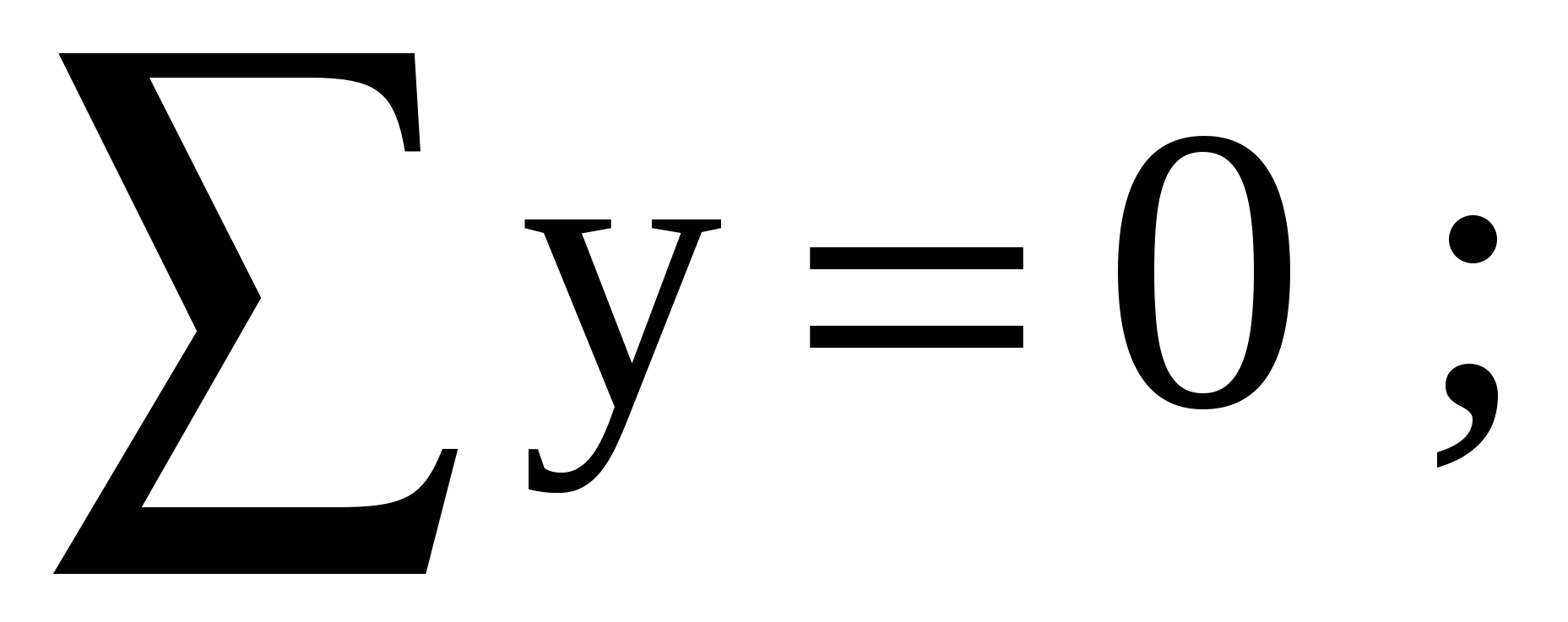
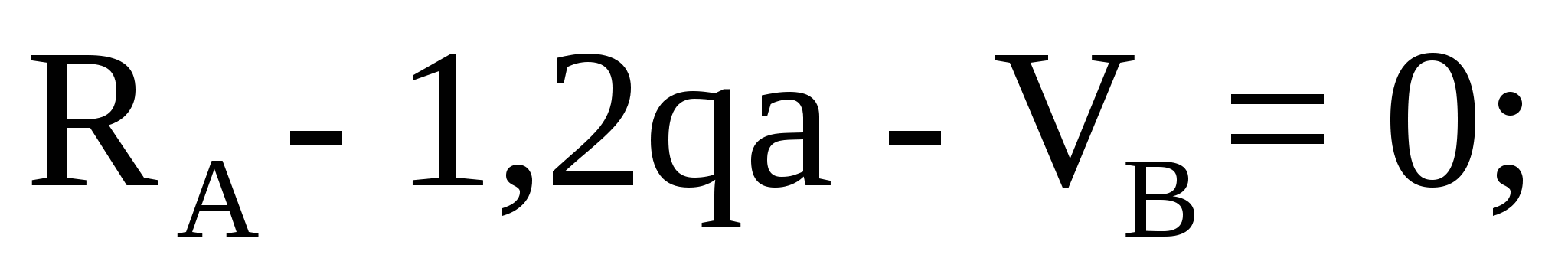
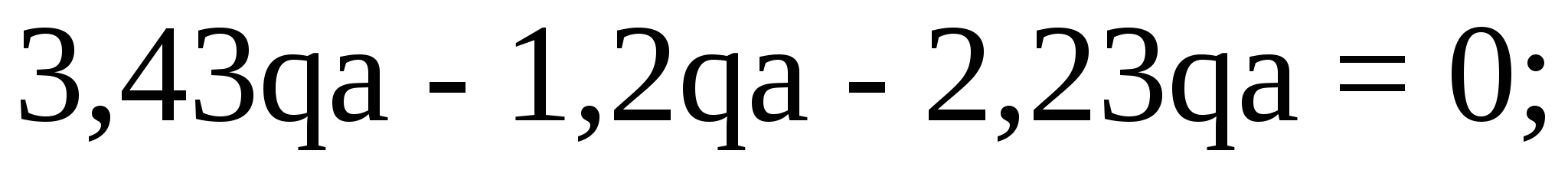

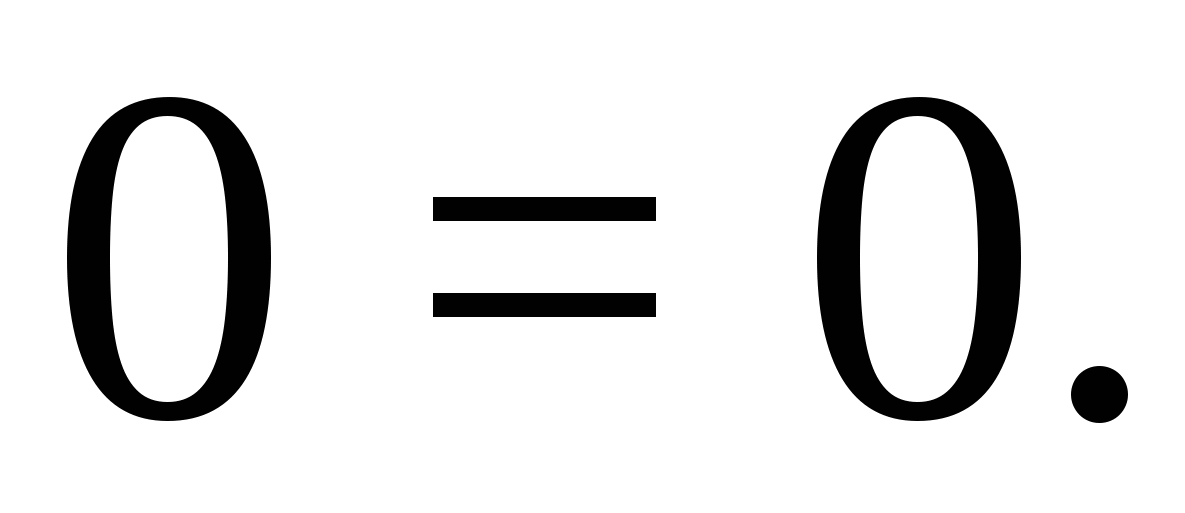
Применяя метод сечений, строим эпюры продольной, поперечной сил и изгибающего момента. Разбиваем раму на четыре силовых участка AС, СD, DЕ, ЕB (рисунок 6.2).
Рассмотрим участок I (AC): 
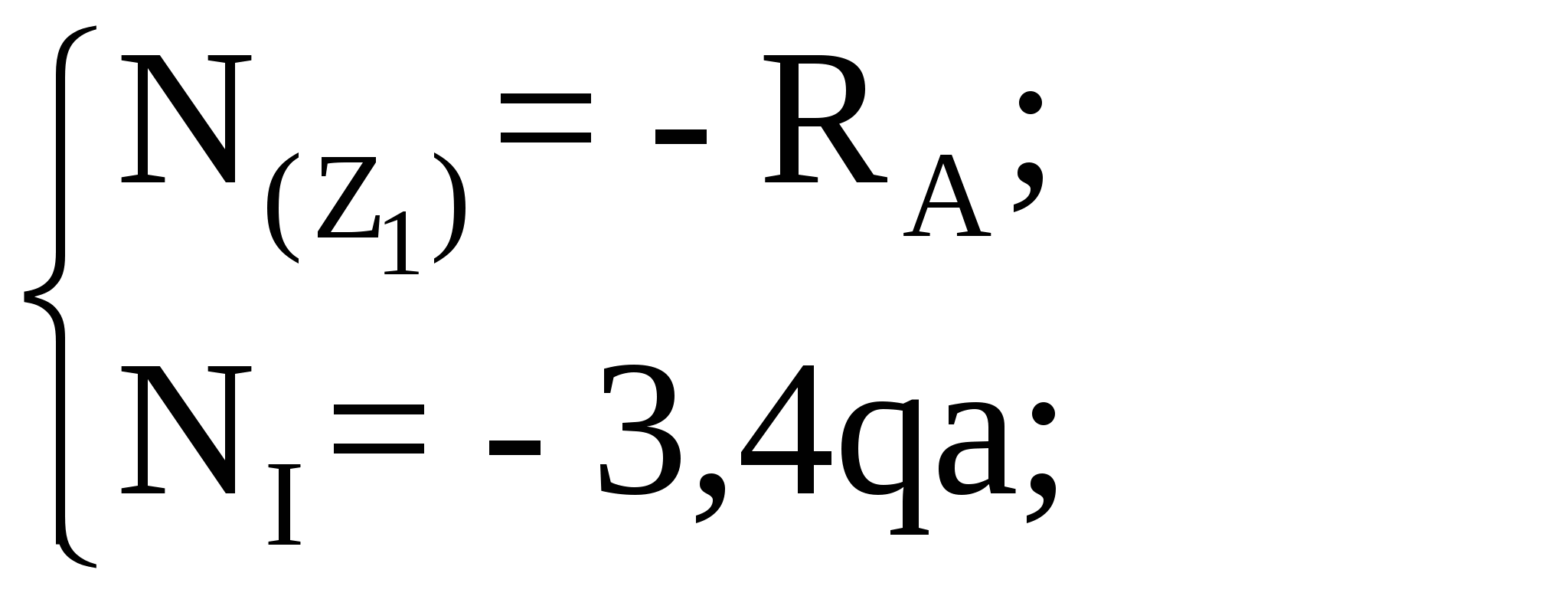
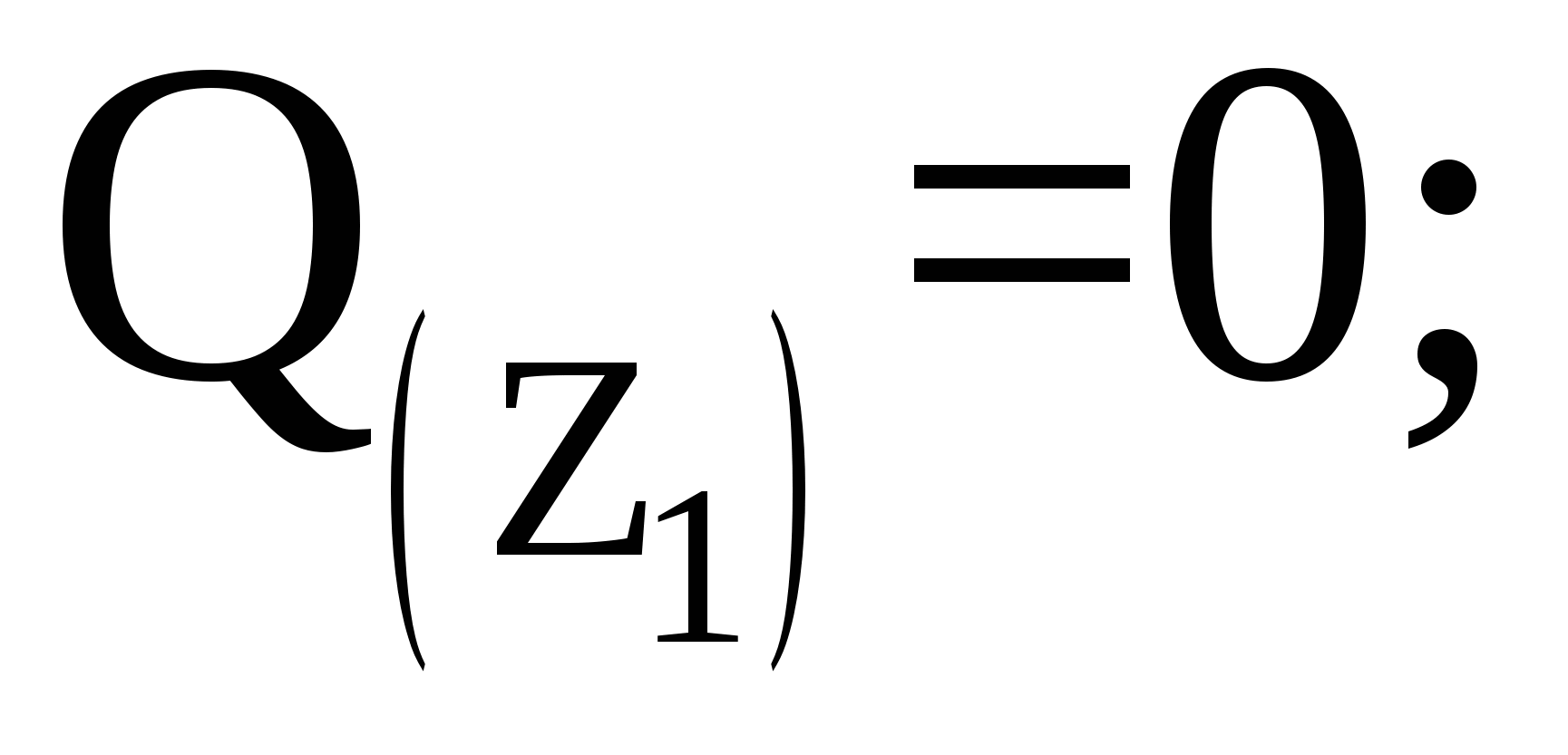

Рассмотрим участок II : 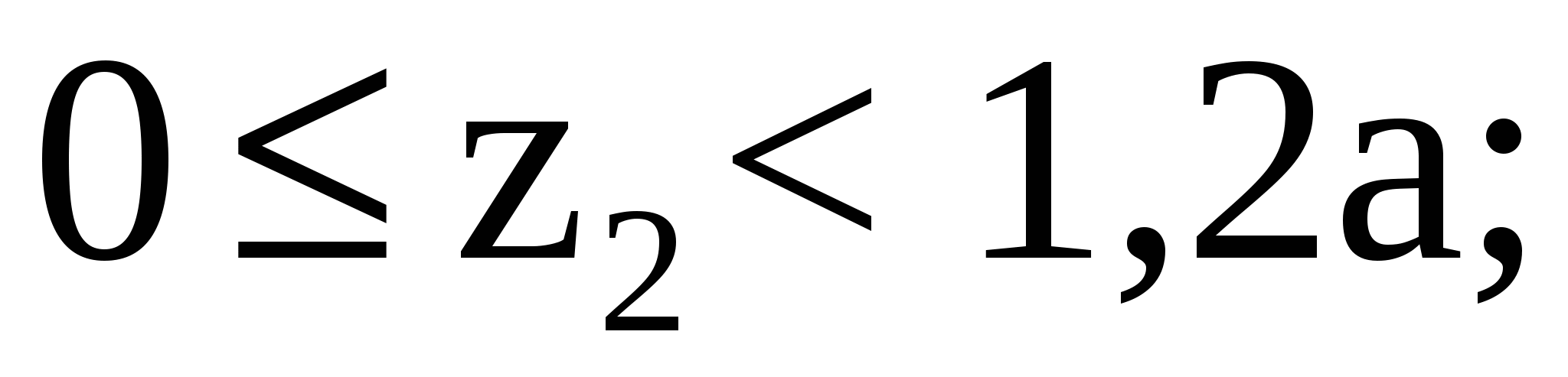

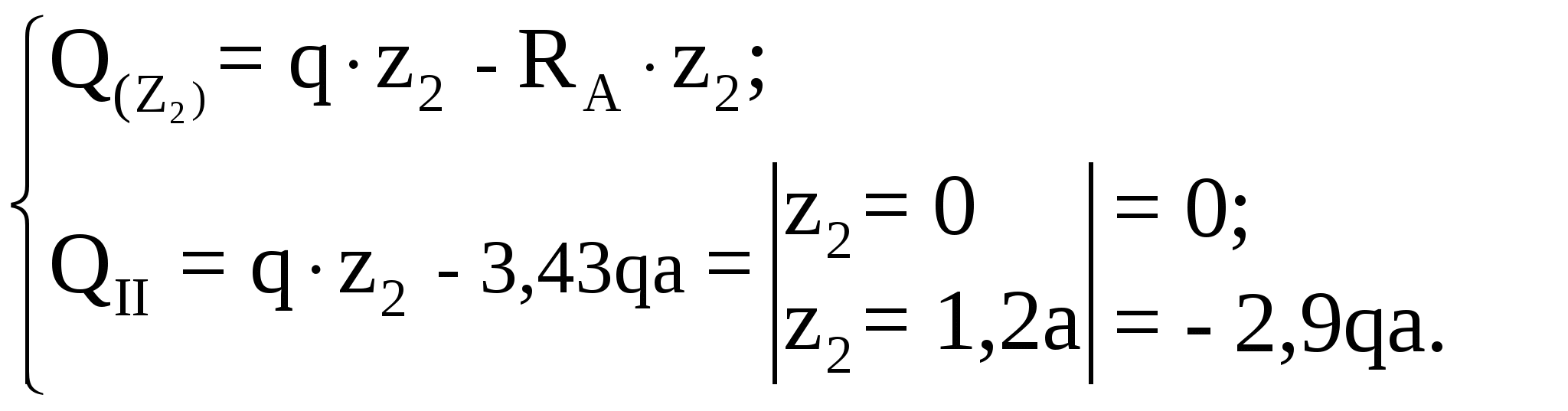
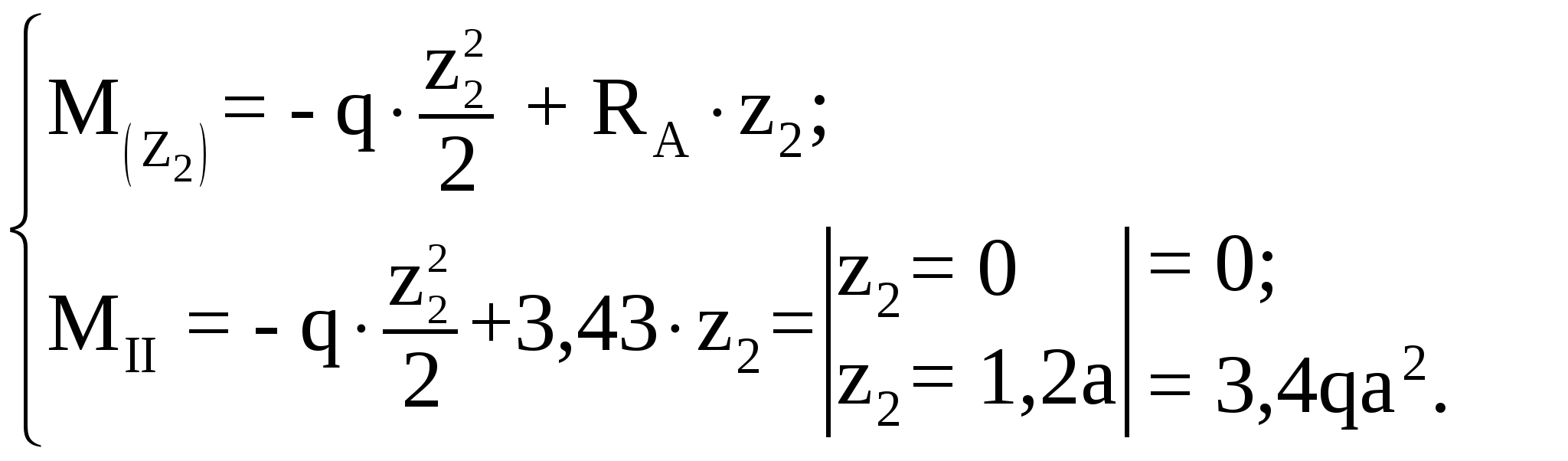
Рассмотрим участок III: 

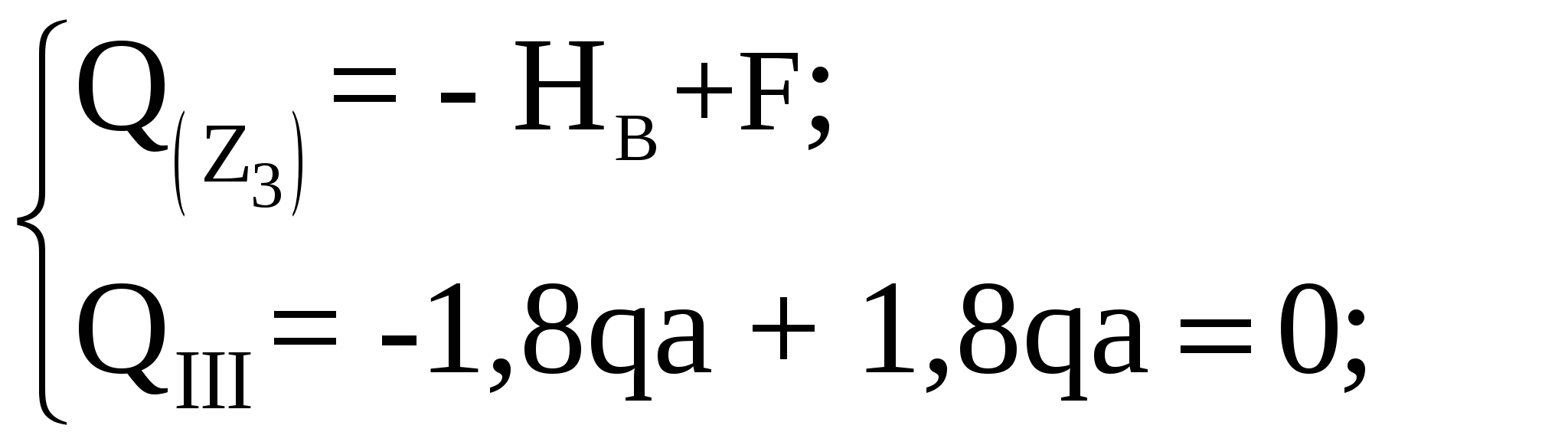
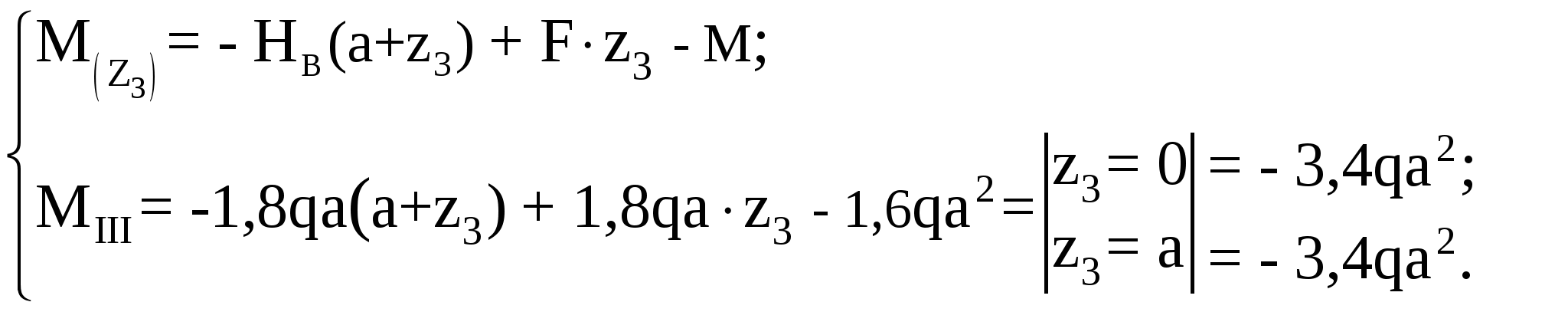
Рассмотрим участок IV: 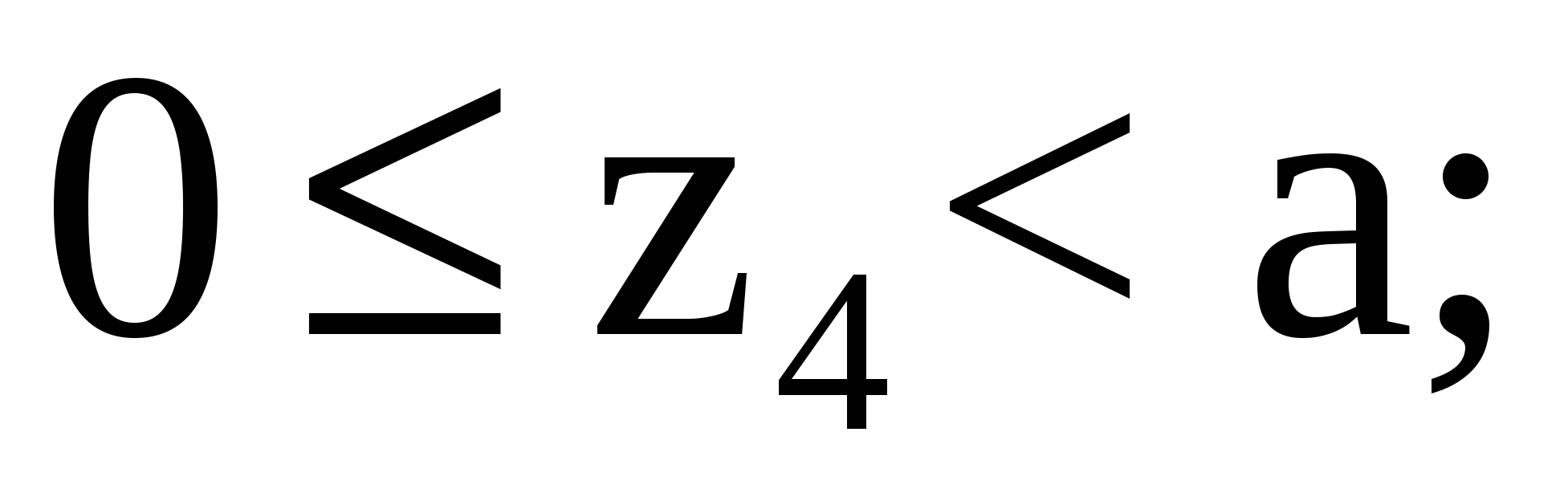
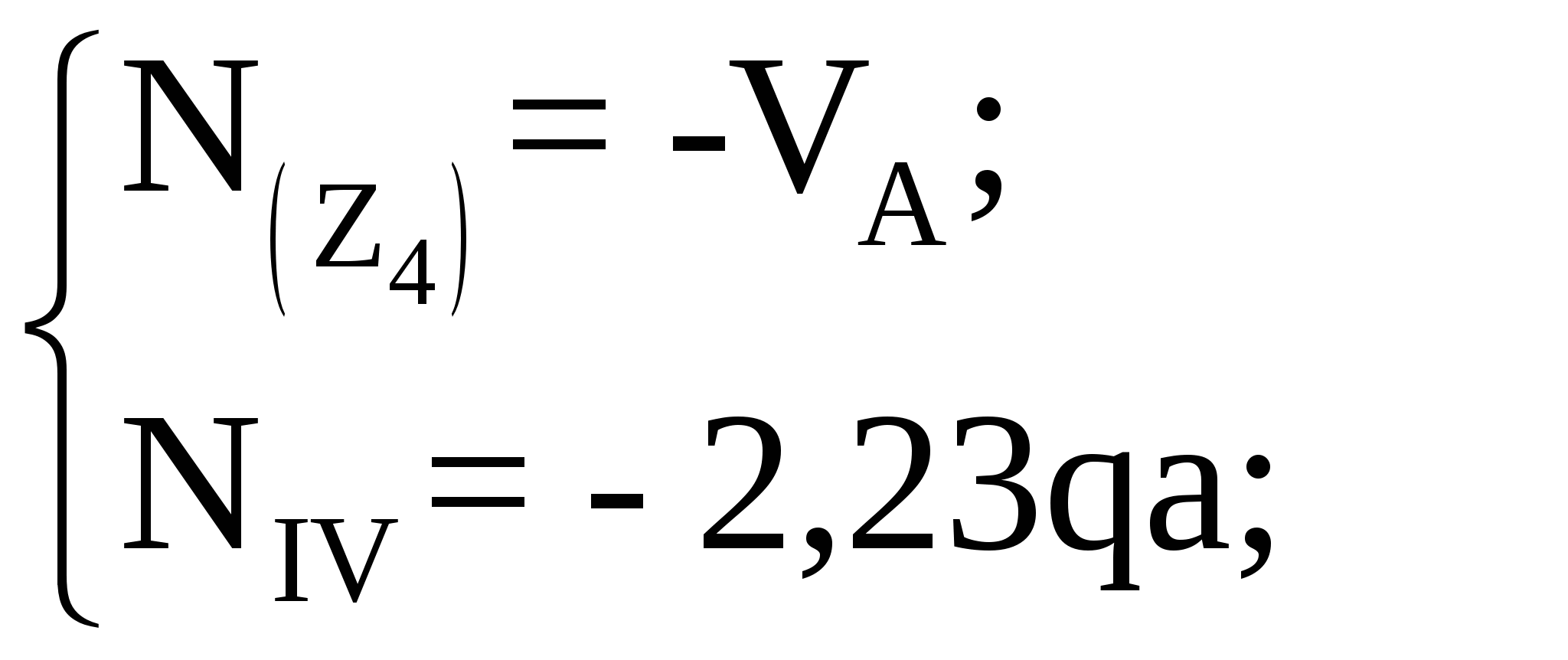

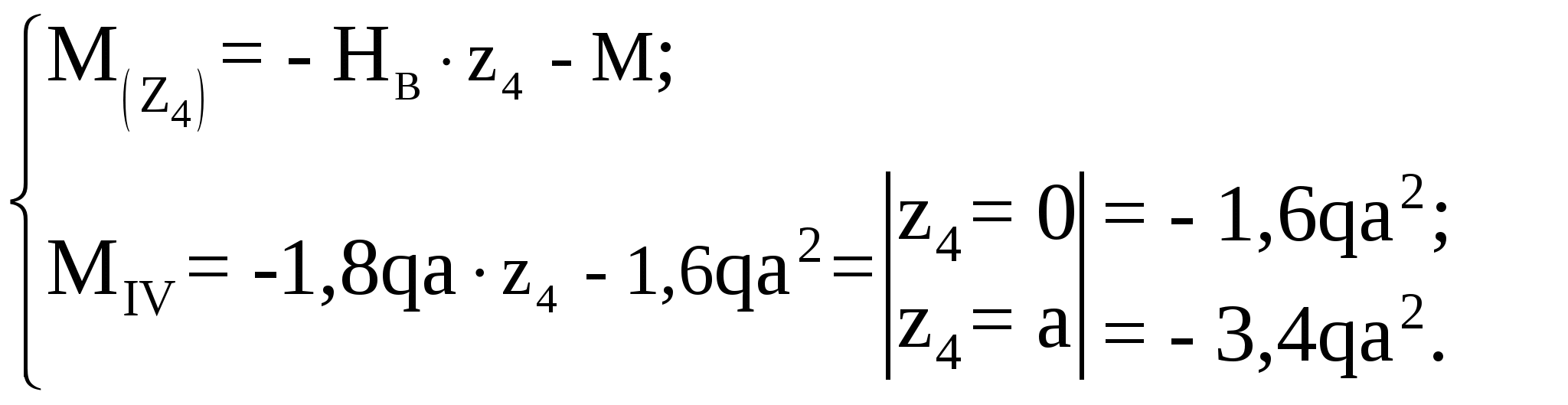
По полученным значениям построены эпюры продольной, поперечной сил и изгибающего момента, которые приведены на рисунке 6.2.
Построенные эпюры поперечной, продольной сил и изгибающего момента проверим путем вырезания узлов рамы и составления схем их равновесия под действием внутренних силовых факторов и внешних нагрузок.
Равновесие узлов C и D представлено на рисунке 6.2.


Рисунок 6.2 – Расчетная схема рамы
ОПНН-241000-02.01.013 РПР
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.